Our purpose is to build an inverse method which best fits a model of artery flow and experimentalmeasurements (we assume that we are able to measure the displacement of theartery as a function of time at three stations).Having no clinical data, we simulate these measurements with thenumerical computations from a "boundary layer" code.First, we revisit the system of Ling and Atabekof boundary layer type for the transmission of a pressure pulsein thearterial system for the case of an elastic wall (but we solve it without any simplification in the $u\partial u/\partial x$ 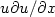term). Then, using a methodanalogous to the well known Von Kármán-Pohlhausen method fromaeronautics but transposed here for a pulsatile flow, we build a system ofthree coupled non-linear partial differential equations depending only ontime and axial co-ordinate. This system governs the dynamics of internalartery radius, centre velocity and a quantity related to the presence ofviscous effects. These two methods give nearly the same numerical results.Second, we construct an inverse method: the aim is to findfor the simpleintegral model, the physical parameters to put in the "boundary layer" code(simulating clinical data). This is done by varying in the integralmodel the viscosity and elasticity in order to fit best with the data. Toachieve this in a rational way, we have to minimise a cost function, whichinvolves the computation of the adjoint system of the integral method. The good setof parameters (i.e. viscosity, and two coefficients of a wall law)is effectively found again. It opens the perspective for application in realclinical cases of this new non-invasive method for evaluating the viscosityof the flow and elasticity of the wall.