Article contents
Absolute intensity calibration of emission spectra: applicationto the forbidden 346 nm nitrogen line for N(2P°) metastable atoms density measurement in flowing afterglow
Published online by Cambridge University Press: 30 May 2008
Abstract
A novel method, based on emission signal from the excitation transfer reaction: Ar*(3P2) + N2(X) $\to $  N2*(C 3 $\Pi_{u}$
N2*(C 3 $\Pi_{u}$ 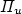 ) + Ar, is proposed for the intensity calibration of the spectroscopic optical detection system in absolute scale. It is applied for the measurement of N(2P°) metastable atoms density in the Short Lived Afterglow (SLA) of a 440 Pa nitrogen discharge produced by a 433 MHz resonant cavity. This density is deduced from the absolute intensity of the forbidden N(2P°–4S°) line at 346.65 nm, whose transition probability is only 0.005 s−1. The N(2P°) density variation in the SLA resembles those of N2(A 3 $\Sigma_{u}$
) + Ar, is proposed for the intensity calibration of the spectroscopic optical detection system in absolute scale. It is applied for the measurement of N(2P°) metastable atoms density in the Short Lived Afterglow (SLA) of a 440 Pa nitrogen discharge produced by a 433 MHz resonant cavity. This density is deduced from the absolute intensity of the forbidden N(2P°–4S°) line at 346.65 nm, whose transition probability is only 0.005 s−1. The N(2P°) density variation in the SLA resembles those of N2(A 3 $\Sigma_{u}$ 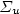 ) metastable molecules and electrons or the emission intensities of first positive (1+), second positive (2+) and first negative (1−) systems of N2. It first decays after the discharge zone up to a minimum and hence increases by almost a factor of thirty to reach a maximum value of 6 × 1017 m−3 at the maximum of the SLA. It is proposed that N(2P°) density results from a local equilibrium between its production: N2(A 3 $\Sigma _{u}^{+}$
) metastable molecules and electrons or the emission intensities of first positive (1+), second positive (2+) and first negative (1−) systems of N2. It first decays after the discharge zone up to a minimum and hence increases by almost a factor of thirty to reach a maximum value of 6 × 1017 m−3 at the maximum of the SLA. It is proposed that N(2P°) density results from a local equilibrium between its production: N2(A 3 $\Sigma _{u}^{+}$ 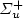 ) + N(4S) $\to $
) + N(4S) $\to $  N(2P) + N2(X 1 $\Sigma _{g}^{+}$
N(2P) + N2(X 1 $\Sigma _{g}^{+}$ 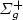 , v) and loss: N2(X 1 $\Sigma _{g}^{+}$
, v) and loss: N2(X 1 $\Sigma _{g}^{+}$ 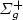 , v≥ 10)+ N(2P) $\to $
, v≥ 10)+ N(2P) $\to $  N2 (A 3 $\Sigma _{u}^{+}$
N2 (A 3 $\Sigma _{u}^{+}$ 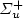 ) + N(4S) reactions, which strongly couple the atomic and molecular metastable states and hence recycle N2(A 3 $\Sigma _{u}$
) + N(4S) reactions, which strongly couple the atomic and molecular metastable states and hence recycle N2(A 3 $\Sigma _{u}$ 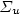 ) metastable molecules produced in the SLA. The balance equation of N(2P°) density provides a N2(X 1 $\Sigma _{g}$
) metastable molecules produced in the SLA. The balance equation of N(2P°) density provides a N2(X 1 $\Sigma _{g}$ 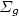 ; v≥ 10) density of 6.5 × 1020 m−3 at the maximum of the SLA. This corresponds to 1% of the total N2 molecules in vibrationally excited levels v≥ 10.
; v≥ 10) density of 6.5 × 1020 m−3 at the maximum of the SLA. This corresponds to 1% of the total N2 molecules in vibrationally excited levels v≥ 10.
Information
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, 2008
References
- 10
- Cited by

