High precision measurements of the celestial coordinates of pulsars are desirable for a number of reasons. If carried out at several epochs, the measurements can yield angular proper motions; together with distance estimates based on dispersion measure, the proper motion of a pulsar reveals two of three components of its space velocity, and consequently provides important kinematic information on pulsar ages (see, for example, Manchester, Taylor and Van 1974; Lyne, Anderson and Salter 1982; and references therein). Direct measurements of annual parallaxes are also possible in principle, and are marginally feasible with present techniques for a few of the closest pulsars. Model independent distances obtained from parallax measurements, together with observed pulsar dispersion measures, yield the electron density along the line of sight to the pulsar. Knowledge of the interstellar electron density in the solar neighborhood provides a calibration of the dispersion-based distance scale that is complementary to the calibration derived from neutral hydrogen absorption measurements of more distant pulsars (Weisberg et al. 1980), and permits appropriate statistical analyses to be made of the local space density of pulsars and their birthrate (e.g. Taylor and Manchester 1977). Finally, pulsar astrometry can be expected to yield important information on the relative orientations of fundamental reference frames. In particular, pulse timing observations yield positions in a reference frame based on motions of the planets, while interferometric position measurements are based on an Earth-equatorial system. At present the relative orientation of these two coordinate systems is known to only 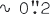 accuracy, though the potential precision of both types of measurements is much higher.
accuracy, though the potential precision of both types of measurements is much higher.