Introduction: The “realist obstacle” to Bruno’s mathematics
Giordano Bruno (1548-1600) owes his reputation to his infinitist cosmology. Indeed, Bruno is known as the ‘philosopher of the infinite’ and, additionally, as an unrepentant heretic because of his death at the hands of the Roman Inquisition. What is less known is that Bruno envisioned not only the infinitely large – the boundless universe – but also the infinitely small – what he called the minimum; and that he spent his last years developing an ‘atomistic geometry’ based on the concept of the minimum. Arguably, the reason why Bruno’s mathematics has gone unnoticed is because even Bruno scholars have struggled to make sense out of it. Although the idea of infinitely small quantities would play a crucial role in the development of seventeenth-century mathematics (leading to the invention of the infinitesimal calculus) Bruno seemed unable to convert this idea into an acceptable mathematical doctrine, probably because he lacked the technical skills to do so. Moreover, Hélène Védrine (Reference Védrine1976) suggested that Bruno’s mathematical failure was also due to his belief in the actual existence of mathematical objects in nature, a belief that constitutes the core of the philosophical view known as “mathematical realism” or “Platonic realism” (see Miller Reference Miller2016). For this reason, Védrine spoke of a “realist obstacle” hindering Bruno’s mathematics.
Recent attempts to gain a better understanding of Bruno’s life and works have led to a reappraisal of his mathematical thought. Giovanni Aquilecchia (Reference Aquilecchia and Aquilecchia1993) was the first to call for a new approach to Bruno’s mathematics based on a careful analysis of his sources, his philosophical agenda, and the historical circumstances under which he came to elaborate his atomistic geometry. Furthermore, Aquilecchia must be credited with the discovery of two of Bruno’s first mathematical writings (the dialogues on Fabrizio Mordente’s compass, Bruno [1586] Reference Bruno and Aquilecchia1957) which remained unknown until the 1950s. In the 2000s, the writings discovered by Aquilecchia provided the basis for Luciana De Bernart’s monograph on Bruno’s mathematics (De Bernart Reference De Bernart2002). For De Bernart, Bruno’s critics made the mistake of reading his mathematical writings through the lens of their own conception of mathematics, while they were best understood in the context of Renaissance mathematical practice. This was confirmed by the dialogues on Mordente’s compass in which Bruno tried to provide a theoretical explanation for the use of the instrument invented by his fellow countryman.
A few years before De Bernart, Angelika Bönker-Vallon had developed new perspectives on Bruno’s mathematics by analyzing it from the viewpoint of his metaphysics (Bönker-Vallon Reference Bönker-Vallon1995).Footnote 1 Likewise, the contributors to the volume edited by Heipcke, Neuser, and Wicke (Reference Heipcke, Neuser and Wicke1991) had paved the way for a new understanding of Bruno’s mathematics by dispelling long-standing prejudices about the derivative nature of Bruno’s atomistic geometry, among other things. Also worth noting is that, as early as the 1920s, Ksenija Atanasijević had offered a detailed account of Bruno’s most important mathematical work in her La doctrine métaphysique de Bruno exposée dans son ouvrage De triplici minimo (The metaphysical and geometrical doctrine of Bruno, as given in his work De triplici minimo (Atanasijević [1922] Reference Atanasijević1972). Although Atanasijević’s interpretation was influenced by her attempt to show that Bruno was a precursor of the Serbian philosopher Branislav Petronijević (1875-1954), her book deserves a special mention because it was written at a time when scholars showed very little interest in Bruno’s mathematics.
In spite of these developments, Bruno continues to be regarded as a poor mathematician.Footnote 2 The aim of this essay is to challenge this received view by charting the evolution of Bruno’s conception of mathematics. I claim that both in his vernacular and Latin works Bruno defended the idea that mathematical objects were mind-dependent, pace Védrine. However, this did not happen at the expense of Bruno’s faith in the explanatory power of mathematics as he repeatedly used mathematical concepts and images in his descriptions of nature, although not in a quantitative way. The only exception to this rule was mathematical astronomy since Bruno disputed that mathematics could capture the physical cause of astronomical phenomena and was against the use of explanatory devices such as orbs. But then again, this was a consequence of Bruno’s disbelief in the existence of mathematical objects outside our minds. A second contention of this paper is that the evolution of Bruno’s mathematics was related to the additions that he made to his theory of the infinite, namely the introduction of the concept of the minimum. In my opinion, it was to turn the minimum into a mathematical object that Bruno started a reform of mathematics.
To be clear, this paper discusses two versions of mathematical realism:
(1) The view that physical phenomena can be explained in mathematical terms.Footnote 3
(2) The view that mathematical objects have an existence that is separate from our mind.
I shall argue that Bruno accepted (1) but not (2). To show how Bruno’s negotiations between these two versions of mathematical realism interacted with the introduction of the minimum, I will examine three works: La cena de le ceneri (Bruno [1584] Reference Bruno and Gatti2018); Acrotismus camoeracensis (Bruno [1588] Reference Bruno and F. Fiorentino1879a); and De minimo (Bruno [1591] Reference Bruno1889b). In particular, I will focus on the cosmological and mathematical implications of Bruno’s discussion of infinity in these three works. However, the reader should be aware that the concept of infinity has a long history that cuts across several disciplines, including theology. Especially in Bruno’s day, advocating an infinitist view of the universe was seen as an attack on the religious status quo, given the dependence of the Christian faith on the Aristotelian-Ptolemaic system. Not to mention the allegations of Pierre Bayle (Reference Bayle1697) who saw in Bruno’s De la causa, principio et uno (On Cause, Principle and Unity; Bruno [1584] Reference Bruno, de Lucca and Richard1998) the archetype of Spinoza’s pantheism. Furthermore, the recent studies of Amir Alexander (Reference Alexander2014) indicate that the infinitely small was also viewed as a troublesome concept by religious authorities such as the Jesuits, who feared its political and social implications for the future of the monarchy and Church hierarchy. It is beyond the scope of this paper to deal with the theological issues raised by Bruno’s conception of infinity. Nonetheless these issues should be kept in mind, otherwise we risk losing sight of the historical context in which Bruno lived and operated and thus underestimating the complexity of his thought.
1. Realism vs instrumentalism in La cena de le ceneri (1584)
Ernan McMullin claimed that “to call Bruno a ‘Copernican’ requires one to empty the label of all content save the assertion that the earth and planets move around the sun” (McMullin Reference McMullin1987, 64). In particular, McMullin noticed how Bruno seemed unable to understand important aspects of the Copernican theory, especially when it came to technical issues. An example is provided by the explanation Bruno gave in La cena de le ceneri (The Ash Wednesday Supper, 1584) of the Copernican diagram showing the position of the planets in the solar system (fig. 1). The issue at stake was the position of the earth relative to the moon. According to Torquato, one of the two Oxford dons with whom Bruno (or better his fictional character) engaged in a conversation on the Copernican theory, Copernicus placed the earth on the third sphere, with the moon carried around it on an epicycle. On the contrary, Bruno thought that the earth and the moon were located on the same epicycle (Bruno Reference Bruno and Gatti2018, 161–65).
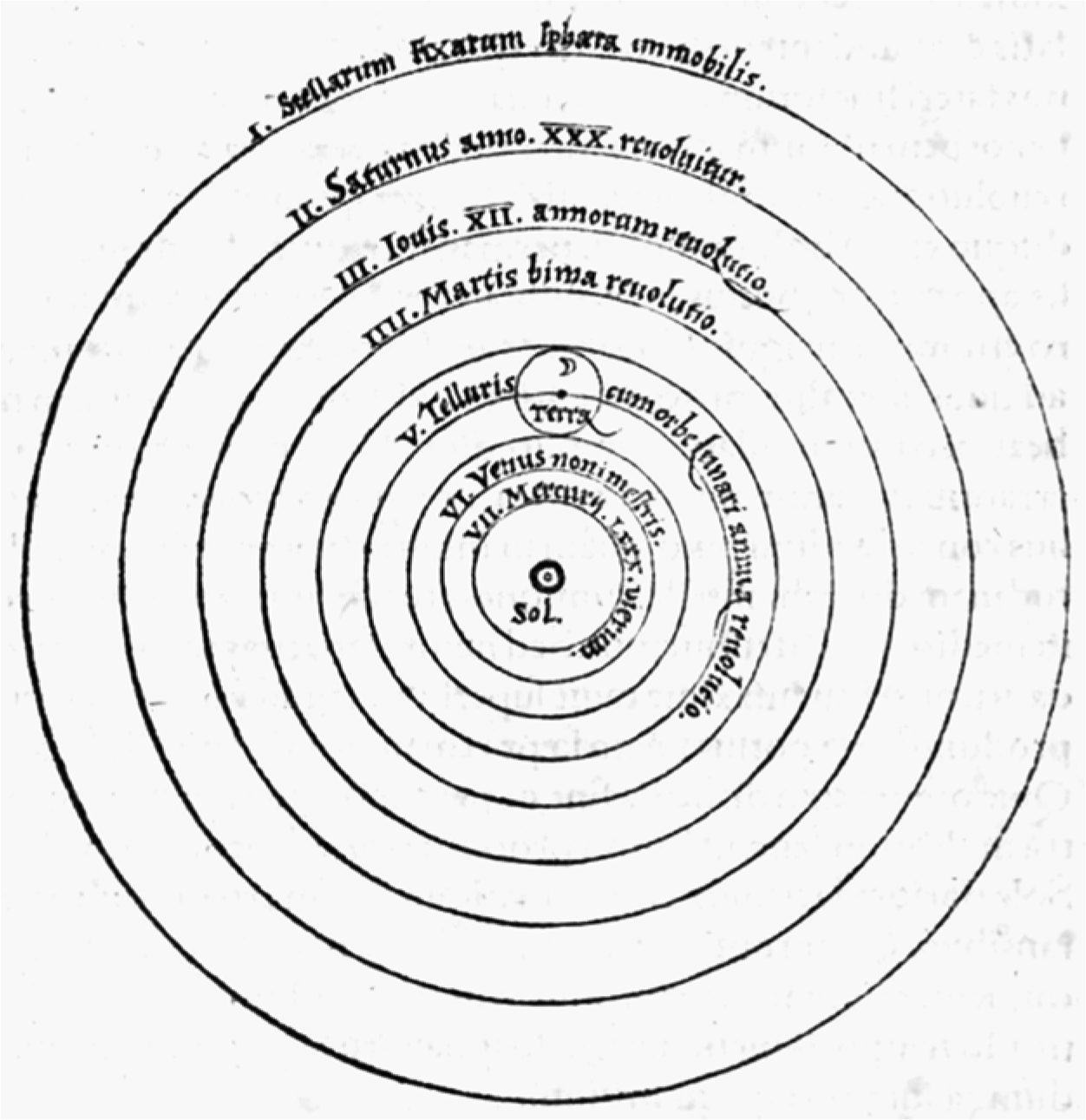
Fig. 1. Diagram showing the position of the planets in the solar system. Copernicus, De revolutionibus, bk. I [in color in the online version only].
Although in La cena Torquato was forced to admit that he was wrong, it was Bruno who made a mistake. In response, scholars have tried to justify him by suggesting external causes for his misunderstanding of the Copernican theory. Frances Yates proposed that Bruno was reading Copernicus in a Hermetic way, which led him to see the Copernican diagram as more of a “hieroglyph” than an actual representation of the solar system (Yates Reference Yates1964, 241).Footnote 4 More recently, Dario Tessicini demonstrated that Bruno’s view that the earth and the moon were on the same epicycle could be traced back to the Pythagorean belief in the existence of a counter-earth (Tessicini Reference Tessicini2007, 9–58).Footnote 5
Be that as it may, Bruno’s failure to understand technical aspects of the Copernican theory does not alter the fact that he was one of the first to explicitly endorse the idea that the earth moved, at a time when the vast majority of the astronomers and natural philosophers tended to accept only Copernicus’s mathematical models but not the underlying cosmological theory. What is more, as noted by McMullin, Bruno may have been the first to notice in print that the author of the anonymous letter entitled Ad lectorem de hypothesibus huius operis (To the reader, regarding the hypotheses of this work) and appended to De revolutionibus (On the Revolutions, 1543) was not Copernicus himself (McMullin Reference McMullin1987, 59).Footnote 6 We now know that the author was Andreas Osiander (1498-1552), who took over the publication of Copernicus’s work when Rheticus was forced to leave Nuremberg for Leipzig, where he had been appointed to the chair of mathematics. However, Bruno could not have been aware of this, as it was not until 1609 that Osiander was first identified as the author of Ad lectorem by Kepler (Lerner and Segonds Reference Lerner and Alain-Philippe2008, 120–24).Footnote 7
In Ad lectorem, Osiander famously claimed that the ideas presented in De revolutionibus had to be regarded as mere hypotheses aimed at explaining astronomical phenomena in mathematical terms, and not as physical statements concerning the actual structure of the universe. In the belief that Copernicus was not only trying his hand at new mathematical models but also proposing an alternative worldview, Bruno criticized the author of Ad lectorem for having betrayed Copernicus’s intentions. Early interpreters, especially Pierre Duhem, have labelled Osiander’s reading of De revolutionibus as instrumentalist, while Bruno and the other scholars who accepted the cosmological aspect of the Copernican theory have been defined as realists. Since the divide between instrumentalism and realism in early modern astronomy has attracted a great deal of scholarly attention, I will give a brief account of the historiographical debate on these two epistemological stances before going on to address the question of Bruno’s realism.
In modern scholarship Pierre Duhem was the first to acknowledge and oppose what, in his understanding, was Copernicus’s realism. In To Save the Phenomena, Duhem claimed that Copernicus was a realist insofar as he believed that his astronomical hypotheses were both true and demonstrable (Duhem [1908] Reference Duhem, Dolan and Maschler1985).Footnote 8 However, Duhem’s claim did not sit well with the findings of Noel Swerdlow and Otto Neugebauer, who showed that Copernicus did not consider his mathematical proofs to be certain (Swerdlow and Neugebauer Reference Swerdlow and Otto1984, 19–21). In light of this, scholars have concluded that Duhem’s hostility towards Copernicus was rooted in his own view of science, one that fiercely rejected “the philosophical-theological imperialism of the prevailing realism of the second half of the sixteenth century” (Goddu Reference Goddu1990, 307). This would also explain why Duhem was sympathetic with Osiander, who in his opinion had shown that “the hypotheses of physics are mere mathematical contrivances devised for the purpose of saving the phenomena” (Duhem Reference Duhem, Dolan and Maschler1985, 117).
A few decades after Duhem, Robert Westman demonstrated that Osiander’s reading of De revolutionibus gave way to an established interpretation of the Copernican theory, which Westman called the “Wittenberg interpretation” and whose advocates were the followers of Philip Melanchthon (1497-1560). This approach was characterized by an ambivalent attitude towards Copernicus, as members of the Melanchthon circle accepted the equantless models while rejecting the three types of terrestrial motion. For this reason, they tried to turn the Copernican models into computational devices that could fit into a geostatic view of the universe. These efforts must have been successful, because “the realist and cosmological claims of Copernicus’s great discovery failed to be given full consideration” (Westman Reference Westman1975, 168). On the other hand, in opposition to Duhem, Westman (ibid., 167) emphasized that the Wittenberg interpretation was not instrumentalist in character, and that “it represented more than a position of epistemic resignation with regard to what one could know about actual celestial motions, while stopping short of a strong realist interpretation” (ibid., 167).
More recently, Peter Barker and Bernard Goldstein warned against the use of the terms realism and instrumentalism in descriptions of sixteenth-century astronomy. Both these terms, the authors argued, were coined in the twentieth century in the context of a specific philosophical debate, hence “neither realism nor instrumentalism quite captures the predicament of the sixteenth-century astronomer” (Barker and Goldstein Reference Barker and Goldstein1998, 253). Moreover, Barker and Goldstein noticed that in the sixteenth century, mathematical astronomy and natural philosophy were distinguished on the basis of their demonstrations. Following the Aristotelian theory, propter quid demonstrations (from causes to effects) were attributed to natural philosophy, while mathematical astronomy was limited to quia demonstrations (from effects to causes). The fact that astronomical knowledge could be probable at best was seen as a consequence of the impossibility of converting quia demonstrations into proper quid, for certain knowledge was achievable only through the latter. It is worth noting that the Aristotelian theory of demonstration was also invoked in another sixteenth-century epistemological debate: the Quaestio de certitudine mathematicarum. Footnote 9 This suggests a comparison between the Quaestio and contemporary discussions on the status of astronomical demonstrations such as those reported by Barker and Goldstein, which would require a separate study.
Returning to Bruno, he has been described as both a straightforward realist (in his commitment to the cosmological significance of Copernicus’s innovations) and as a fierce opponent of the mathematics of his time. In fact, it was Bruno himself who conveyed this image by endorsing Copernicus on the one hand, and by writing One Hundred and Sixty Articles against the Mathematicians (Articuli centum et sexaginta adversus mathematicos, Bruno [1588] Reference Bruno1889a) on the other hand. How did Bruno’s realism fit with his mistrust in mathematics? Hélène Védrine claimed that it was because of his realism that Bruno was skeptical about contemporary mathematical research. For Védrine, Bruno was a realist in a Platonic sense insofar as he thought that “mathematical beings were in act in the sensible world” (Védrine Reference Védrine1976, 40. All translations are my own unless otherwise specified). On the contrary, sixteenth-century mathematics was for the most part based on the Aristotelian view that mathematical objects were intelligible concepts abstracted from sensible beings. Rejecting this Aristotelian ontology and the mathematics that was built on it, Bruno went on to propose his own ‘Platonic’ version of mathematics, central to which was the concept of ‘real’ minima.Footnote 10 However, Védrine noted that it was not Bruno but “the Paduan Aristotelians, Cardano, Tartaglia, Scipione del Ferro who contributed to the advancement of sixteenth-century mathematics” (ibid., 241).
As mentioned in the introduction, I challenge Védrine’s view of Bruno’s mathematics. I will show that if it is true that traces of realism can be found in Bruno’s vernacular works (and in particular in La cena), then these works also contain the seeds of a different epistemology that will be fully developed in the Latin works. Let us start by reviewing the evidence in favor of Bruno’s realism. Scholars, including Védrine, have regarded Bruno’s critique of Osiander and the consequent defense of Copernicus’s ‘true’ intentions as an endorsement of realism. In effect, this appears to be the most plausible explanation for the passages in question, which can be summarized as follows.
Not only was Bruno one of the first to note that the author of Ad lectorem could not have been Copernicus, he was probably the author of the first vernacular translation of the letter (see Lerner Reference Lerner2012). A comparison with the original text shows that Bruno faithfully translated its content, omitting only a section in which Osiander reiterated what he had already said about the use of hypotheses in astronomy – a use that was made necessary by the fact that astronomical reasoning could by no means yield knowledge of the physical causes of celestial phenomena. This was indeed the central point of Ad lectorem which ended with following words (taken from Bruno’s translation):
Let us then take advantage of the treasure of these suppositions only in so far as they render the art of calculation marvelously easy. For if anyone takes such fictions for real, he will leave this discipline more ignorant than when he entered it (Bruno Reference Bruno and Gatti2018, 93).
As anticipated, Bruno utterly rejected this reading of De revolutionibus which he regarded as the work of an “ignorant and presumptuous ass” (Bruno Reference Bruno and Gatti2018, 91). In particular, what Bruno did not accept of Ad lectorem was its attempt to excuse Copernicus, as if the Polish astronomer wanted to defend himself from the charges of heterodoxy and heresy that theologians and Aristotelians could have pressed against his book.Footnote 11 As a matter of fact, modern Copernicus scholarship has shown that this was precisely the case, as Copernicus was afraid of how De revolutionibus could be received by the learned audience.Footnote 12 For this reason, Bruce Wrightsman wrote that “it is much more probable to claim that, for over a century, ‘Ad lectorem’ protected the work … during an extremely tense period of ideological and political conflict and thus, actually permitted the work to be used and pondered during that period by those with such scruples” (Wrightsman Reference Wrightsman and Robert1975, 240).Footnote 13
To dismiss Osiander’s arguments and prove that it was Copernicus’s purpose to claim that the earth moved, Bruno made the argument that De revolutionibus was a philosophical rather than a mathematical treatise. As we have seen, the distinction between natural philosophers and mathematicians was at the center of sixteenth-century astronomical debates. According to Bruno, Copernicus viewed himself as philosopher when, writing to Pope Paul III in the preface to De revolutionibus, he underscored the importance of paying attention to the philosophers and not to the “vulgar herd” (Bruno Reference Bruno and Gatti2018, 93).Footnote 14 On the other hand, Bruno could not deny that Copernicus’s work contained mathematical demonstrations, which however he regarded as a mere exercise and not as an integral part of the Copernican theory. For this reason, Bruno concluded, Copernicus “not only acts as the mathematician who makes suppositions, but also as the physicist who demonstrates the movements of the earth” (ibid.).
If La cena contained only this judgment of Copernicus and his theory, we should conclude that Bruno was a realist insofar as he not only considered the terrestrial motions to be more than a mathematical hypothesis, but also attributed this opinion to Copernicus himself. However, when earlier in the text Smithus asked Theophilus (Bruno’s spokesman) what was his opinion about Copernicus, Theophilus answered that:
His judgement in matters of natural philosophy was far superior to that of Ptolemy, Hipparchus, Eudoxus, and all the others who followed in their footsteps. … Yet he did not leave this philosophy far enough behind him; for, in so far as he was a student of mathematics rather than of nature, he was unable to penetrate those depths which would have allowed him to eradicate the useless and inappropriate principles from which it stems. (Bruno Reference Bruno and Gatti2018, 29)
Hence, Bruno had an ambivalent attitude towards Copernicus. At the outset of La cena, Copernicus was criticized for being more of a mathematician than a natural philosopher. On the contrary, in his defense of the reality of the Copernican model, Bruno emphasized the physical value of the ideas presented in De revolutionibus. How can this ambivalence be explained? McMullin wrote that “Copernicus appears as a philosopher in search of the truth by contrast with other astronomers, but as a ‘mathematician’ by contrast with Bruno himself” (McMullin Reference McMullin1987, 63). This may be true, but it was McMullin himself who was the one to notice that there were more differences than similarities between Bruno’s and Copernicus’s cosmological theories. An analysis of these differences will lead to a revaluation of Bruno’s realism by shedding new light on the question of whether he considered mathematical objects to be in act in the sensible world (as Védrine had it) or not.
Let us begin by reviewing Bruno’s considerations about astronomical calculations. These calculations were the result of hundreds of years of astronomical observations. Being aware of this, Bruno gave credit to the generations of mathematicians whose work had laid the foundation for the cosmological theories of Ptolemy and Copernicus. Yet there was another side to Bruno’s assessment of mathematical astronomy, as illustrated in the following passage:
Such men [i.e. the mathematicians] are like interpreters who translate words from one language into another; yet it is not they but others who finally reach the heart of the matter. Again, they are like rustics who report the progress and fortunes of a battle to an absent captain; although they themselves are unable to understand the strategies, the causes and the design which have led to the victory. (Bruno Reference Bruno and Gatti2018, 27)
Two remarks are in order. First, in this quotation, Bruno once again emphasized that the “rustic” mathematicians did not know the causes of astronomical phenomena, whose knowledge instead belonged to the so-called “captain,” whom we can assume to be the military counterpart of the natural philosopher. Hence, this quotation corroborates the idea that Bruno accepted the distinction, standard in his day, between mathematical astronomy and natural philosophy.
The second remark is that, for Bruno, mathematicians acted like interpreters, their task being to translate the language of nature into that of mathematics. Consider for a moment the Galilean metaphor of the book of nature written in the language of mathematics. Although there is no consensus on the meaning attached by Galileo to it (see Palmerino Reference Palmerino, Gorham, Hill, Slowik and Kenneth Waters2016), it should be evident that such a metaphor stood at the opposite pole from the Brunian view that in astronomical studies mathematicians played the role of interpreters. The idea underlying this view was indeed that the language of mathematics was different from that of nature, otherwise there would be no need for an interpreter. At the same time, it should be noted that comparing mathematicians and interpreters did not amount to saying that it took a mathematician to understand nature, as Bruno made it clear that mathematicians lacked this ability, which was only possessed by natural philosophers.
Hence, we can conclude that Bruno did not think that the universe had a mathematical structure. Rather, the universe could be described in mathematical terms, but this required a translation which, as faithful as it might be, could not entirely capture the essence of the physical reality. This is also confirmed by Bruno’s rejection of circular devices, especially orbs, as a way of explaining planetary motions, which was arguably the most significant difference between Bruno’s and Copernicus’s cosmological theories. In La cena Bruno took issue with “those who want to imagine fillings and wadding of irregular orbs, … inventing plasters and other prescriptions in order to heal nature so that it can serve their master, Aristotle or someone else” (Bruno Reference Bruno and Gatti2018, 115). As is evident from the reference to Aristotle, Bruno here was attacking the advocates of the Aristotelian-Ptolemaic system. However, the same objection could be raised against Copernicus, who also conceived the existence of solid orbs in which heavenly bodies were embedded.
In Bruno’s cosmological theory, orbs were dismissed in favor of “a single airy, ethereal, spiritual, and liquid body, a capacious place of motion and quiet, which reaches out into the immensity of infinity” (ibid., 117). Having abandoned the solid orbs which carried around the heavenly bodies in a uniform circular motion, Bruno was forced to find an alternative physical explanation for planetary motions. To this end, he resorted to the original Platonic idea, whose major promoter in the Renaissance was Marsilio Ficino, that heavenly bodies were animals, meaning that they were inhabited by a spirit called the world-soul or anima mundi (see Pompeo Faracovi Reference Pompeo Faracovi2002). It was this world-soul that was responsible for the motion of heavenly bodies, which wandered across the ethereal space and around their respective suns – Bruno envisioned infinite solar systems – to absorb the heat and light necessary to life.Footnote 15
Let us now ask: on what grounds did Bruno reject the existence of solid orbs? Was this rejection caused by something more than his outspoken criticism of Aristotle and his epigones? In nature, Bruno argued, no body had a perfectly round shape, nor was there a body which moved along a perfectly circular trajectory. Thus, why was perfect circularity to be found in the heavens, as postulated by those who assumed the existence of solid orbs (Bruno Reference Bruno and Gatti2018, 115)? This argument implied that, unlike what most of medieval cosmologists thought, there was no difference between the bodies that inhabited the super- and sublunary regions. Indeed, as is well known, such a distinction was absent from Bruno’s homogenous universe in which all bodies were composed of the same four elements. Furthermore, this argument tells us that, contrary to what Védrine claimed, Bruno did not believe in the actual existence of mathematical objects (such as perfect circles or circular motions) in the physical world. Based on the same argument, in the later Latin works Bruno would go on to dismiss all circular astronomical devices, including eccentrics and epicycle (more on this in § 3). At that point, instead of criticizing the astronomers who “healed” nature so as to fit their mathematical models, he would argue that it was mathematics that had to change in order to represent nature, thus advocating a reform of geometry. This reform was to make room for a new concept that meanwhile had entered Bruno’s mathematics: the concept of the minimum.
2. Acrotismus camoeracensis (1588) and the making of Bruno’s theory of minima
It was in the dialogues on the proportional compass invented by the Italian geometer Fabrizio Mordente (Bruno [1586] Reference Bruno and Aquilecchia1957) that Bruno first attributed a mathematical meaning to the minimum.Footnote 16 There, he showed that Mordente’s compass made it possible to demonstrate that both mathematical and physical objects had an atomic structure. More precisely, in Bruno’s understanding – but not in Mordente’s, who vehemently protested against this interpretation of his instrument – the compass allowed one to divide curved and straight lines down to their minimum, indivisible fractions. This discovery must have inspired Bruno to further develop his atomistic geometry. However, in order to do so, he needed to overcome what during the Middle Ages and still in his day represented the major obstacle to atomism: the Aristotelian criticisms. He attended to this task in another work that was composed at about the same time as the dialogues on Mordente’s compass, but was published two years later: Acrotismus camoeracensis (Bruno [1588] Reference Bruno and F. Fiorentino1879a).Footnote 17 Perhaps not coincidentally, Acrotismus also yielded insights into the issue of Bruno’s mathematical realism.
Already in La cena Bruno maintained that “in physics, division of a finite body cannot progress to infinity expect for those who are mad, whether you think of it in act or in potential” (Bruno Reference Bruno and Gatti2018, 107). However, neither in La cena nor in the other Italian dialogues did Bruno explain why it was so “mad” to believe in the infinite divisibility of the physical continuum, thus postulating rather than rationally justifying the existence of the atoms. To a certain extent, Acrotismus filled this gap. The structure of the book, which followed the model of sixteenth-century academic discussions, was designed to address one by one the central issues raised in Aristotle’s Physics and De caelo. To the problem of whether or not the continuum was infinitely divisible (which was mainly discussed in Book VI of Aristotle’s Physics), Bruno devoted the 42nd article of Acrotismus, which reads as follows:
Before assuming the continuum to be infinitely divisible, Aristotle should have specified how the whole universe was divisible in the same way as this earth, and the whole of this globe in the same way as this apple; how these things, which qua finite beings are of different size, through infinite division become equal. … How are they equal in potency, but unequal in act?Footnote 18
For Bruno, to say that two things were infinitely divisible was to say that they were composed of an infinite number of parts. Infinity, however, admitted no difference as it was impossible for “an infinite to be bigger than another infinite neither in potency nor in act.”Footnote 19 By the same token, it was impossible to say which of two infinitely divided things was bigger than the other, since after the division both would turn out to be composed of the same infinite number of parts. Nor did it matter that the parts of one thing were bigger in size than the parts of the other, “for the bigger parts taken only once from the bigger [thing] would be necessarily equal to the smaller parts taken multiple times from the smaller [thing].”Footnote 20 The Aristotelians would have replied to these objections by pointing out – as done in the pseudo-Aristotelian treatise De insecabilibus lineis (On indivisible lines) – that the fact that a bigger object could contain an infinite number of smaller objects told us nothing about the containing object itself, for one object could be contained in another without being part of it.Footnote 21
This counterargument did not seem to bother Bruno, who instead focused on another Aristotelian distinction – that between potential and actual infinity. In the Physics Aristotle viewed the infinite divisibility of the continuum as a potential infinity, meaning that there was no limit to the number of parts into which the continuum could be divided; no matter how small a part was, it could always be further divided.Footnote 22 In addition, Aristotle made it clear that the divisibility of the continuum was never infinite in an actual sense, since in his opinion actual infinity was impossible.Footnote 23 Bruno challenged this claim, as he did not see how it was possible for a potency to exist without a corresponding act. Bruno assumed that an Aristotelian would reply that such potencies were found in the realm of mathematics, where it was allowed to perform operations that were impossible to perform in the real world. In response, Bruno noted that even the mathematicians did not take the line to be “absolutely infinite, as it would be useless to do so, but they consider it to be infinite in a certain respect, as, for them, infinite means ‘as large as you want’.”Footnote 24 On this point, Bruno was in complete agreement with Aristotle, who in the Physics wrote that mathematicians made use of arbitrary large and not infinite magnitudes.Footnote 25
It is beyond the purpose of this paper to discuss the effectiveness of Bruno’s arguments against the Aristotelian physics. Rather, I am interested in what these arguments can tell us about Bruno’s conception of mathematics and its relationship to the idea of infinity. We have seen that Bruno (as well as Aristotle) thought that, strictly speaking, it was not the infinitely great but the arbitrary large to be the subject of mathematics. What about the infinitely small? Did, according to Bruno, mathematicians believe that there was a limit to the division of the mathematical continuum, or did they believe that it could go on to infinity? We know that classical Euclidean geometry advocated an Aristotelian view of the continuum insofar as the only allowed indivisibles were points, lines, and planes, conceived as ends and not as parts of the continuum. In fact, most of the medieval objections to atomism were inspired by mathematical considerations (Lüthy, Murdoch, and Newman Reference Lüthy, Murdoch and Newman2001). For example, critics of atomism noted that it was impossible to account for incommensurables when magnitudes were conceived as composed of a finite number of indivisible parts. Bruno himself had to reply to this objection in De minimo. In Acrotismus he chose a different strategy, one that at first sight may appear rhetorical, but that retrospectively may be viewed as the inception of Bruno’s project of mathematical reform:
It is one thing to consider magnitude mathematically, quite another to consider magnitude physically. … If logic and mathematics want to assume the infinitely divisible regardless of any praxis and use for a vain consideration, let them have their way.Footnote 26
Mathematics for Bruno had to conform to the natural order, lest it became a vain speculation. This meant that the infinite divisibility of the continuum had to be rejected both in physics and mathematics. With the passing of time Bruno realized that it took more than a few adjustments to introduce atomism into mathematics; in fact, it required an entirely new theory, the development of which was carried out in De minimo. As for Acrotismus, it seemed to imply that Bruno was far from being a mathematical realist. In it, instead of saying that physical phenomena could be fully explained in mathematical terms (as the mathematical realist would do), Bruno claimed that it was mathematics that had to be modelled after physics. However, it should be noted that in other passages of the same work Bruno was willing to attribute a role to mathematics in physical explanations. This was the case of the third and fourth article of Acrotismus, in which Bruno advocated a return to the pre-Socratic philosophy in the face of Aristotle’s dismissal of it. Taking inspiration from Parmenides and Melissus, Bruno (1879, 98–9) defended the idea that the universe was an ‘infinite sphere’ – an image which often occurred in Bruno’s works and to which we shall return in the next section. Thus, Bruno allowed the use of mathematical images as metaphors. In particular, he relied on these images to express those concepts that exceeded the limits of human understanding, such as the infinity of the universe. This metaphorical version of mathematical realism was not incompatible with the idea that the existence of mathematical objects depended on our mind. Indeed, both these conceptions were in the background of Bruno’s atomistic geometry, although their overlap was not without problems, as the next section will show.
3. De minimo (1591): Where mathematics meets physics (and metaphysics)
In the spring of 1591, Giordano Bruno was in Frankfurt when he was invited to Venice by the patrician Giovanni Mocenigo (Firpo Reference Firpo and Quaglioni1993, 154–55). This gave Bruno the opportunity to return to his home country, from where he had escaped more than ten years earlier under the suspicion of heresy. Bruno must have been aware that, once in Italy, the Inquisition could have pressed charges against him. Nevertheless, he accepted Mocenigo’s invitation and, against his better judgment, set off to Venice. As is well known this decision turned out to be unfortunate since, after being denounced by Moceningo in 1592 and a long inquisitorial process, Bruno was burned at the stake in Campo de’ Fiori in Rome on 17 February 1600.
Bruno’s activities had been brought to Mocenigo’s attention by the Latin poem entitled De minimo, which together with De immenso and De monade formed Bruno’s so-called ‘Frankfurt trilogy’. Indeed, all of these three works were published in Frankfurt shortly before Bruno left for Italy. For his part, Mocenigo was interested in unlocking the secrets of the art of memory which Bruno mastered. More relevant to this study, De minimo marked the end of the mathematical journey started eight years earlier with the Italian dialogues, as it contained the ultimate version of Bruno’s theory of minima. In his previous works, Bruno had criticized contemporary mathematical research for its failure to acknowledge the importance of the minimum: ‘The ignorance of the minimum makes the geometers of this century geameters, and the philosophers philasophers’ Bruno wrote in Articuli adversus mathematicos. Footnote 27 This criticism continued in De minimo where, building on the premise that physical reality had an atomic structure, the bone of contention became the infinite divisibility of the mathematical continuum:
When infinitely dividing what has a precise measure, the geometer makes a mistake, he does not follow in the footsteps of nature which, being never reached, cannot be imitated by the geometer.Footnote 28
If in Acrotismus the acceptance by mathematicians of infinite divisibility was tolerated (“let them have their way”), in De minimo Bruno was less indulgent. This was probably due to the fact that in the Latin poem Bruno presented his own mathematical theory, which he viewed as an alternative to classical mathematics. As a matter of fact, Bruno’s theory of minima was one of the first attempts to introduce indivisibles into geometry, an issue that would become central to seventeenth-century mathematics. On the other hand, there was the role (or lack thereof) of mathematics in the study of nature. As is evident from the above quotation, Bruno thought of mathematics as a set of mental representations that had to mirror rather than explain the physical world. Once again, this suggests that Bruno was far removed from the Galilean metaphor of the book of nature, and more generally from what has been called the mathematization of nature.Footnote 29 In fact, if anything, the project carried out by Bruno may be said to be a naturalization of mathematics.Footnote 30
However, one may argue that Bruno’s attitude towards mathematics was not consistent throughout De minimo. At the outset of this work, especially, Bruno seemed to envision an intimate relation between mathematics and nature:
God is the monad source of all numbers, the simplicity of all magnitudes and the substance of all compounds … Nature is the numerable number, the measurable magnitude, and the determinable reality. Reason is the number that numerates, the magnitude that measures and the reality that determines.Footnote 31
This mathematized view of nature was grounded in the concept of the monad – one of the cornerstones of Bruno’s ontology as well as the reason why scholars have suggested a connection between Bruno and Leibniz.Footnote 32 Bruno defined the monad as the minimum of numbers rationally [rationaliter] and of all things essentially [essentialiter].Footnote 33 In turn, this definition laid the foundation for the numerological project carried out in De minimo and, more extensively, in De monade (Bruno [1591] Reference Bruno1884). A discussion of Bruno’s numerology would require a separate study. It suffices to say that Bruno’s speculations on the symbolic and mystical powers of numbers rested on the panpsychist view of the world already expressed in his vernacular works. Accordingly, Bruno’s numerology opened the door to a form of ‘mathematical magic’ rather than to a quantitative analysis of physical phenomena.Footnote 34 This is also the reason why Bruno has not been admitted into the canon of modern science, despite his pioneering defense of Copernicus and the infinity of the universe. The historian of the Scientific Revolution Alexandre Koyré was among the first to voice concerns about Bruno’s lack of modernity, although he stressed the importance of the new cosmological paradigm brought about by the Italian philosopher:
Giordano Bruno, I regret to say, is not a very good philosopher. The blending together of Lucretius and Nicholas of Cusa does not produce a very consistent mixture. … He is a very poor scientist, he does not understand mathematics, and his conception of the celestial motions is rather strange. … As a matter of fact, Bruno’s world-view is vitalistic, magical; his planets are animated beings that move freely through space of their own accord like those of Plato and Pattrizi. Bruno’s is not a modern mind by any means. Yet his conception is so powerful and so prophetic, so reasonable and so poetic that we cannot but admire it and him. And it has—at least in its formal features—so deeply influenced modern science and modern philosophy, that we cannot but assign to Bruno a very important place in the history of the human mind. (Koyré Reference Koyré1958, 54; emphasis added)
Bruno did not believe in the existence of universal laws of nature that could be formulated in mathematical terms. Rather, numbers and figures could be applied to the study of nature only insofar as they were capable of taking on a symbolic and metaphorical meaning. If this aspect of Bruno’s conception of mathematics may seem ambiguous or raise doubts, there is no question about his commitment to the view that mathematical objects did not exist in nature. We have seen that in La cena solid orbs (still employed by Copernicus) were rejected in favor of a universe populated by animated celestial bodies, the reason being that no perfect circular form or motion was to be found in nature. This was reaffirmed in the Frankfurt poems, especially in De immenso (Bruno [1591] Reference Bruno1879b) where Bruno denied that the perfect circle – in fact, any perfect form – was present in nature.Footnote 35 However, there was an aspect of Bruno’s theory of minima that contrasted with his denial of the independence of mathematical objects from our mind: the circular shape of the minimum. Bruno, indeed, claimed that the minimum was a circle in two-dimensional space and a sphere in three-dimensional space.Footnote 36 But why did Bruno endow the most important entity in his ontology with a circular shape, if such a shape was nowhere to be found in the real world?
The problem of the circular shape of the Brunian minimum is even more compelling if we consider the importance that Bruno attributed to images, and more in general to visual thinking.Footnote 37 In the specific case of Bruno’s mathematical works, images had a double application. First, images offered a means to promote mathematics as a practical discipline. An example is provided by the “temples” of Apollo, Minerva, and Venus that Bruno constructed in De minimo, by means of which he aimed to lay the foundations for a universal theory of measurement that would enable mathematical practitioners to measure everything (figs. 2a-2b-2c). In addition, Bruno used mathematical images in a symbolic fashion to express what was difficult to put into words, or to visualize what was invisible to the human eye. For instance, in De minimo Bruno relied on circular constructions to show the patterns in which atoms were arranged to form mathematical and physical figures (figs. 3a-3b-3c).

Fig. 2a. Atrium Veneris [in color in the online version only].

Fig. 2b. Atrium Minervae [in color in the online version only].

Fig. 2c. Atrium Apollinis [in color in the online version only].

Fig. 3a. Area Democriti [in color in the online version only].

Fig. 3b. Campus Democriti [in color in the online version only].

Fig. 3c. Isocheles Democriti [in color in the online version only].
Christoph Lüthy (Reference Lüthy1998) demonstrated that Bruno inherited these circular diagrams from a centuries-old tradition, going all the way back to Augustine (354-430 AD) and based on the mathematical teachings of Boethius (477-524 AD). What distinguished Bruno from his predecessors was the meaning that he attached to those diagrams, as he was the first to use circles to represent atoms. In parallel, Bruno was the recipient of a metaphor which also had its origin in the Middle Ages, in particular in the anonymous Liber XXIV philosophorum (Book of the 24 Philosophers): the metaphor of the infinite sphere whose center was everywhere and whose circumference was nowhere.Footnote 38 Originally devised as a description of God, the metaphor of the infinite sphere took on different meanings throughout its long history, depending on the context in which it was understood. With Nicholas of Cusa, the infinite sphere came to represent the universe, the maximum in the realm of finite beings.Footnote 39 In keeping with the idea (also from Cusa) that the opposites coincided, Bruno took a step further and employed the metaphor of the infinite sphere to describe the minimum:
It is evident to everybody that the center, i.e. the circle, the chord, the area, the diameter, the arc and the radius are all without distinction, whether we refer to the minimum or to the maximum.Footnote 40
Hence, the circular shape of the Brunian minimum appeared to result from the interplay of two theoretical elements: the circular diagrams and the metaphor of the infinite sphere. Despite their geometric appearance, both these elements had a metaphysical rather than a strictly mathematical origin, as they were used to symbolize God.Footnote 41 It was Bruno who turned the circular diagrams and the infinite sphere into full-fledged mathematical notions. He did so by employing them as a visual aid to understanding the fundamental properties of the minimum (e.g. the way in which minima interact with one another). Nevertheless, the metaphysical heritage of these two notions interfered with their new mathematical function, causing problems at the geometric level. For instance, since around one circle there was only room for six other circles with the same diameter (see Area Democriti, fig. 3a) and since each circle stood for a geometric point, Bruno concluded that in a circumference the center (the central circle) was reached by only six radii (whose extremities were the six peripherical circles).Footnote 42
Thus, the circular shape of the minimum was at odds not only with Bruno’s rejection of the mental independence of mathematical objects, but also with the basic tenets of Euclidean geometry. As seen above, these contradictions were generated by the introduction of metaphysical elements into a theory that was at once physical and mathematical. Nonetheless, Bruno was unwilling to abandon those metaphysical elements because his objective was precisely to integrate physics, metaphysics, and mathematics into a single theory. In fact, the whole of Bruno’s theory was built on the distinction of the three species of minima: physical (the atom), metaphysical (the monad), and mathematical (the point).Footnote 43 This meant that all of these three aspects of reality could be described in terms of minima, or that in Bruno’s understanding the minima provided a ‘theory of everything.’
Bruno may or may not have been aware that his project was too ambitious, and that any attempt to unify physics, metaphysics, and mathematics would have caused problems at one or more of these three levels. What is certain is that he was willing to face these problems to ensure the comprehensiveness of his theory. This does not alter the fact that Bruno’s theory of minima was flawed, particularly with regard to its mathematical and physical applications. However, acknowledging that Bruno’s theory served a ‘higher purpose’ may help to better assess its overall value.
Conclusion
Bruno was a classic example of Renaissance polymath. In a relatively short amount of time (from 1582 to 1591) he composed more than forty works both in vernacular and in Latin, which covered a wide range of subjects, from natural magic to cosmology, from mathematics to the art of memory. Regardless of their subject matter, all of Bruno’s works had a philosophical inspiration; in fact, they were aimed at promoting Bruno’s own philosophy, a system in which elements from different traditions (Neoplatonism, Hermeticism, Lullism, Copernicanism, just to mention the most important) were originally integrated to create an alternative to the prevailing Aristotelian philosophy. Bruno’s philosophical project also informed his treatment of strictly non-philosophical subjects such as mathematics. In this paper, I have shown how Bruno’s conception of mathematics changed in accordance with his concept of infinity, arguably the subject on which Bruno’s polemic with the Aristotelians was more heated. If for the Aristotelians infinity could be potential and not actual, Bruno admitted the existence of both the infinitely large (the maximum) and the infinitely small (the minimum). His atomist geometry, with its blend of mathematical realism and mental dependence of mathematical objects, was thus the result of his efforts to translate the minimum into a mathematical entity.
In addition, my analysis has shown that, instead of explaining nature in strictly mathematical terms, Bruno preferred to use mathematical images as metaphors (e.g. the infinite sphere) or to attribute a symbolic function to mathematical concepts (e.g. the monad). In this respect, Bruno does not fit into the narrative of the Scientific Revolution as told by Husserl ([1936] Reference Husserl, Carr and Evanston1970) and Koyré (Reference Koyré1958), among others. This narrative was based on the assumption that the rise of modern science coincided with the emergence of a quantitative approach to the study of nature. The mathematization of nature has since become the epitome of the Scientific Revolution. But what if mathematizing was not the only available approach? What if there were more “forms of mathematization” (Roux Reference Roux2010) or there were scholars who tried to naturalize mathematics? The invention of the calculus provides evidence that, as it was, classical mathematics was unable to account for natural phenomena such as motion (see Berlinski Reference Berlinski1995). Bruno was aware of this, as proved by the fact that he argued against those who wanted to force nature into predetermined mathematical models (e.g. the Ptolemaic astronomers). What if the modernity of Bruno’s mathematics consisted in this awareness? Will it lead us to reconsider his mathematical abilities, and perhaps the whole relationship between early modern mathematics and the Scientific Revolution? This study is a first step in this direction.
Acknowledgments
The author would like to thank prof. Miguel A. Granada for reading and commenting on an early draft of this article. The same gratitude is extended to the anonymous reviewers, whose remarks have contributed to improve the quality of the article.
Paolo Rossini is a historian of philosophy and science, specialized in the Renaissance and early modern period. He is Marie Skłodowska-Curie Fellow at the Erasmus School of Philosophy of Rotterdam, where he runs the EU-funded project “Cartesian Networks.”










