Article contents
People search via deep compressed sensing techniques
Published online by Cambridge University Press: 02 February 2022
Abstract
People search can be reformulated as submodular maximization problems to achieve solutions with theoretical guarantees. However, the number of submodular function outcome is 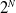 $2^N$ from N sets. Compressing functions via nonlinear Fourier transform and spraying out sets are two ways to overcome this issue. This research proposed the submodular deep compressed sensing of convolutional sparse coding (SDCS-CSC) and applied the Topological Fourier Sparse Set (TFSS) algorithms to solve people search problems. The TFSS is based on topological and compressed sensing techniques, while the CSC is based on DCS techniques. Both algorithms enable an unmanned aerial vehicle to search for the people in environments. Experiments demonstrate that the algorithms can search for the people more efficiently than the benchmark approaches. This research also suggests how to select CSC or TFSS algorithms for different search problems.
$2^N$ from N sets. Compressing functions via nonlinear Fourier transform and spraying out sets are two ways to overcome this issue. This research proposed the submodular deep compressed sensing of convolutional sparse coding (SDCS-CSC) and applied the Topological Fourier Sparse Set (TFSS) algorithms to solve people search problems. The TFSS is based on topological and compressed sensing techniques, while the CSC is based on DCS techniques. Both algorithms enable an unmanned aerial vehicle to search for the people in environments. Experiments demonstrate that the algorithms can search for the people more efficiently than the benchmark approaches. This research also suggests how to select CSC or TFSS algorithms for different search problems.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 1
- Cited by

