Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ji, Wenqiang
Ma, Min
and
Qiu, Jianbin
2019.
A new fuzzy sliding mode controller design for delta operator time-delay nonlinear systems.
International Journal of Systems Science,
Vol. 50,
Issue. 8,
p.
1580.
Wang, Huan
Yang, Yuzheng
Fei, Juntao
and
Fang, Yunmei
2019.
Adaptive control of micro-electro-mechanical system gyroscope using neural network compensator.
Advances in Mechanical Engineering,
Vol. 11,
Issue. 12,
Keighobadi, Jafar
Hosseini-Pishrobat, Mehran
and
Faraji, Javad
2020.
Adaptive neural dynamic surface control of mechanical systems using integral terminal sliding mode.
Neurocomputing,
Vol. 379,
Issue. ,
p.
141.
Pan, Yongping
Joo, Young‐Hoon
and
Yu, Haoyong
2020.
On performance recovery of robust dynamic surface control.
International Journal of Robust and Nonlinear Control,
Vol. 30,
Issue. 8,
p.
3094.
Hosseini‐Pishrobat, Mehran
Keighobadi, Jafar
Pirastehzad, Armin
and
Javad Yazdanpanah, Mohammad
2021.
Immersion and invariance‐based extended state observer design for a class of nonlinear systems.
International Journal of Robust and Nonlinear Control,
Vol. 31,
Issue. 13,
p.
6233.
Shao, Xingling
Shi, Yi
Zhang, Wendong
and
Cao, Huiliang
2021.
Neurodynamic Approximation-Based Quantized Control With Improved Transient Performances for Microelectromechanical System Gyroscopes: Theory and Experimental Results.
IEEE Transactions on Industrial Electronics,
Vol. 68,
Issue. 10,
p.
9972.
Vafaie, Reza Hadjiaghaie
Mohammadzadeh, Ardashir
and
Piran, Md. Jalil
2021.
A new type-3 fuzzy predictive controller for MEMS gyroscopes.
Nonlinear Dynamics,
Vol. 106,
Issue. 1,
p.
381.
Zhang, Rui
Xu, Bin
and
Shi, Peng
2022.
Output Feedback Control of Micromechanical Gyroscopes Using Neural Networks and Disturbance Observer.
IEEE Transactions on Neural Networks and Learning Systems,
Vol. 33,
Issue. 3,
p.
962.
Shao, Xingling
Si, Haonan
and
Zhang, Wendong
2022.
Low-frequency learning quantized control for MEMS gyroscopes accounting for full-state constraints.
Engineering Applications of Artificial Intelligence,
Vol. 115,
Issue. ,
p.
104724.
Zhang, Haichuan
and
Chen, Fei
2022.
Observer-based prescribed performance tracking control for MEMS Gyroscope subject to input saturation.
Nonlinear Dynamics,
Vol. 110,
Issue. 4,
p.
3395.
Wang, Duansong
Kong, Min
Zhang, Gang
and
Liang, Xiaoling
2022.
Adaptive Second-Order Fast Terminal Sliding-Mode Formation Control for Unmanned Surface Vehicles.
Journal of Marine Science and Engineering,
Vol. 10,
Issue. 11,
p.
1782.
Luo, Shaohua
Yang, Guanci
Li, Junyang
and
Ouakad, Hassen M.
2022.
Dynamic analysis, circuit realization and accelerated adaptive backstepping control of the FO MEMS gyroscope.
Chaos, Solitons & Fractals,
Vol. 155,
Issue. ,
p.
111735.
Wu, Xiang
Lu, Qun
She, Jinhua
Sun, Mingxuan
Yu, Li
and
Su, Chun-Yi
2023.
On convergence of extended state observers for nonlinear systems with non-differentiable uncertainties.
ISA Transactions,
Vol. 136,
Issue. ,
p.
590.
Tarani, Sina Ebrahimzadeh
Abdi, Siamak
and
Beyramzad, Jalil
2023.
Prescribed performance output feedback controller design for MEMS gyroscopes using adaptive integral terminal SMC and high-order sliding mode observer.
p.
633.
Li, Qinsheng
and
Ding, Birong
2023.
Design of Backstepping Sliding Mode Control for a Polishing Robot Pneumatic System Based on the Extended State Observer.
Machines,
Vol. 11,
Issue. 9,
p.
904.
Liu, Liyan
Shen, Gang
Wang, Wei
Li, Xiang
and
Zhu, Zhencai
2024.
Neural adaptive dynamic surface control for position tracking of electrohydraulic servo systems based on extended state observer.
Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering,
Vol. 238,
Issue. 9,
p.
1535.
Gao, Min
Li, Jing
Hu, Taihong
Luo, Jin
and
Feng, Baidong
2024.
Intelligent vehicle trajectory tracking with an adaptive robust nonsingular fast terminal sliding mode control in complex scenarios.
Scientific Reports,
Vol. 14,
Issue. 1,
Jeong, Hoijo
Suk, Jinyoung
and
Kim, Seungkeun
2024.
Control of quadrotor UAV using variable disturbance observer-based strategy.
Control Engineering Practice,
Vol. 150,
Issue. ,
p.
105990.
Zhang, Rui
Xu, Bin
Li, Shihua
and
Gao, Guangen
2024.
Recursive integral terminal sliding mode control with combined extended state observer and adaptive Kalman filter for MEMS gyroscopes.
International Journal of Robust and Nonlinear Control,
Vol. 34,
Issue. 9,
p.
5706.
Meng, Qinghua
Zhang, Ze-Kun
and
Sun, Zong-Yao
2025.
Distributed driving electric vehicle lateral stability control method considering time delay.
Measurement and Control,
Vol. 58,
Issue. 7,
p.
947.
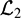 $\mathcal{L}_2$-robust ESO is phrased as a convex optimization problem in terms of linear matrix inequalities (LMIs). Next, by using the estimated velocity and disturbance, a certainty equivalence tracking controller is designed based on DSC. To achieve an improved robustness and to remove static steady-state tracking errors, new non-linear integral error surfaces are incorporated into the DSC. Based on the energy-to-peak (
$\mathcal{L}_2$-robust ESO is phrased as a convex optimization problem in terms of linear matrix inequalities (LMIs). Next, by using the estimated velocity and disturbance, a certainty equivalence tracking controller is designed based on DSC. To achieve an improved robustness and to remove static steady-state tracking errors, new non-linear integral error surfaces are incorporated into the DSC. Based on the energy-to-peak (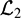 $\mathcal{L}_2$-
$\mathcal{L}_2$-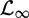 $\mathcal{L}_\infty$) performance criterion, a finite number of LMIs are derived to obtain the DSC gains. In order to prevent amplification of the measurement noise in the DSC error dynamics, a multi-objective convex optimization problem, which guarantees a prescribed
$\mathcal{L}_\infty$) performance criterion, a finite number of LMIs are derived to obtain the DSC gains. In order to prevent amplification of the measurement noise in the DSC error dynamics, a multi-objective convex optimization problem, which guarantees a prescribed 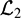 $\mathcal{L}_2$-
$\mathcal{L}_2$-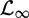 $\mathcal{L}_\infty$ performance bound, is considered. Finally, the efficacy of the proposed control method is illustrated by detailed software simulations.
$\mathcal{L}_\infty$ performance bound, is considered. Finally, the efficacy of the proposed control method is illustrated by detailed software simulations.
