Published online by Cambridge University Press: 21 October 2020
In his Tractatus, Wittgenstein maintained that arithmetic consists of equations arrived at by the practice of calculating outcomes of operations 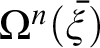 $\Omega ^{n}(\bar {\xi })$
defined with the help of numeral exponents. Since
$\Omega ^{n}(\bar {\xi })$
defined with the help of numeral exponents. Since 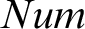 $Num$
(x) and quantification over numbers seem ill-formed, Ramsey wrote that the approach is faced with “insuperable difficulties.” This paper takes Wittgenstein to have assumed that his audience would have an understanding of the implicit general rules governing his operations. By employing the Tractarian logicist interpretation that the N-operator
$Num$
(x) and quantification over numbers seem ill-formed, Ramsey wrote that the approach is faced with “insuperable difficulties.” This paper takes Wittgenstein to have assumed that his audience would have an understanding of the implicit general rules governing his operations. By employing the Tractarian logicist interpretation that the N-operator 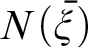 $N(\bar {\xi })$
and recursively defined arithmetic operators
$N(\bar {\xi })$
and recursively defined arithmetic operators 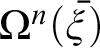 $\Omega ^{n}(\bar {\xi })$
are not different in kind, we can address Ramsey’s problem. Moreover, we can take important steps toward better understanding how Wittgenstein might have imagined emulating proof by mathematical induction.
$\Omega ^{n}(\bar {\xi })$
are not different in kind, we can address Ramsey’s problem. Moreover, we can take important steps toward better understanding how Wittgenstein might have imagined emulating proof by mathematical induction.