Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-11T12:41:24.440Z Has data issue: false hasContentIssue false
  • English
  • Français

THREE MODEL-THEORETIC CONSTRUCTIONS FOR GENERALIZED EPSTEIN SEMANTICS

Part of: General logic Model theory

Published online by Cambridge University Press:  08 July 2021

KRZYSZTOF A. KRAWCZYK
KRZYSZTOF A. KRAWCZYK*
Affiliation:
DEPARTMENT OF LOGIC NICOLAUS COPERNICUS UNIVERSITY IN TORUŃ TORUŃ, POLAND E-mail: krawczyk@doktorant.umk.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper introduces three model-theoretic constructions for generalized Epstein semantics: reducts, ultramodels and 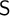$\textsf {S}$-sets. We apply these notions to obtain metatheoretical results. We prove connective inexpressibility by means of a reduct, compactness by an ultramodel and definability theorem which states that a set of generalized Epstein models is definable iff it is closed under ultramodels and 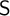$\textsf {S}$-sets. Furthermore, a corollary concerning definability of a set of models by a single formula is given on the basis of the main theorem and the compactness theorem. We also provide an example of a natural set of generalized Epstein models which is undefinable. Its undefinability is proven by means of an 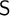$\textsf {S}$-set.

Keywords

Epstein semanticsS-setultramodelreductdefinability

MSC classification

Primary: 03B60: Other nonclassical logic
Secondary: 03C20: Ultraproducts and related constructions 03C80: Logic with extra quantifiers and operators
Type
Research Article
Information
The Review of Symbolic Logic , Volume 15 , Issue 4 , December 2022 , pp. 1023 - 1032
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Carnielli, W. (1987). Methods of proofs of relatedness and dependence logic. Reports on Mathematical Logic, 21, 35–46.Google Scholar
Del Cerro, L. F., & Lugardon, V. (1991). Sequents for dependence logics. Logique et Analyse, 133/134, 57–71.Google Scholar
Epstein, R. L. (1979). Relatedness and implication. Philosophical Studies, 36(2), 137–173.CrossRefGoogle Scholar
Epstein, R. L. (1987). The algebra of dependence logic. Reports on Mathematical Logic, 21, 19–34.Google Scholar
Epstein, R. L. (1990). The Semantic Foundations of Logic. Vol. 1: Propositional Logics. Nijhoff International Philosophy Series, Vol. 35. Dordrecht: Springer.Google Scholar
Epstein, R. L. (2005). Paraconsistent logics with simple semantics. Logique et Analyse, 48(189/192), 71–86.Google Scholar
Iseminger, G. (1986). Relatedness logic and entailment. The Journal of Non-Classical Logic, 3(1), 5–23.Google Scholar
Jarmużek, T., & Kaczkowski, B. (2014). On some logic with a relation imposed on formulae: Tableau system F. Bulletin of the Section of Logic, 43(1/2), 53–72.Google Scholar
Jarmużek, T., & Klonowski, M. (2020). On logic of strictly deontic modalities. Semantic and tableau approach. Logic and Logical Philosophy, 29(3), 335–380.Google Scholar
Klonowski, M. (2020). Aksjomatyzacja monorelacyjnych logik wiażacych (Axiomatisation of Monorelational Relating Logics). PhD Thesis, Nicolaus Copernicus University in Toruń.Google Scholar
Krajewski, S. (1982). On relatedness logic of Richard L. Epstein. Bulletin of the Section of Logic, 11(1/2), 24–30.Google Scholar
Krajewski, S. (1986). Relatedness logic. Reports on Mathematical Logic, 20, 7–14.Google Scholar
Krajewski, S. (1991). One or many logics? (Epstein’s set-assignment semantics for logical calculi). The Journal of Non-Classical Logic, 8(1), 7–33.Google Scholar
Malinowski, J., & Palczewski, R. (2020). Relating semantics for connexive logic. In Logic in High Definition. Trends in Logical Semantics. Berlin: Springer.Google Scholar
Paoli, F. (1993). Semantics for first degree relatedness logic. Reports on Mathematical Logic, 27, 81–94.Google Scholar
Paoli, F. (1996). S is constructively complete. Reports on Mathematical Logic, 30, 31–47.Google Scholar
Walton, D. N. (1979a). Philosophical basis of relatedness logic. Philosophical Studies, 36(2), 115–136.CrossRefGoogle Scholar
Walton, D. N. (1979b). Relatedness in intensional action chains. Philosophical Studies, 36(2), 175–223.CrossRefGoogle Scholar