Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-11T14:57:43.976Z Has data issue: false hasContentIssue false
  • English
  • Français

TEMPORAL INTERPRETATION OF MONADIC INTUITIONISTIC QUANTIFIERS

Part of: General logic

Published online by Cambridge University Press:  02 December 2021

GURAM BEZHANISHVILI  and
LUCA CARAI
GURAM BEZHANISHVILI
Affiliation:
DEPARTMENT OF MATHEMATICAL SCIENCES NEW MEXICO STATE UNIVERSITY LAS CRUCES, NM 88003, USA E-mail: guram@nmsu.edu
LUCA CARAI*
Affiliation:
DIPARTIMENTO DI MATEMATICA UNIVERSITÀ DEGLI STUDI DI SALERNO FISCIANO 84084, ITALY
*
E-mail: lcarai@unisa.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that monadic intuitionistic quantifiers admit the following temporal interpretation: “always in the future” (for 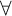$\forall $ ) and “sometime in the past” (for $\exists $ ). It is well known that Prior’s intuitionistic modal logic ${\sf MIPC}$ axiomatizes the monadic fragment of the intuitionistic predicate logic, and that ${\sf MIPC}$ is translated fully and faithfully into the monadic fragment 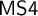${\sf MS4}$ of the predicate 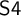${\sf S4}$ via the Gödel translation. 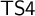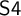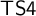To realize the temporal interpretation mentioned above, we introduce a new tense extension ${\sf TS4}$ of ${\sf S4}$ and provide a full and faithful translation of ${\sf MIPC}$ into ${\sf TS4}$ . We compare this new translation of ${\sf MIPC}$ with the Gödel translation by showing that both 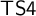${\sf TS4}$ and 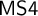${\sf MS4}$ can be translated fully and faithfully into a tense extension of 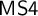${\sf MS4}$ , which we denote by 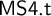${\sf MS4.t}$ . This is done by utilizing the relational semantics for these logics. As a result, we arrive at the diagram of full and faithful translations shown in Figure 1 which is commutative up to logical equivalence. We prove the finite model property (fmp) for 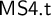${\sf MS4.t}$ using algebraic semantics, and show that the fmp for the other logics involved can be derived as a consequence of the fullness and faithfulness of the translations considered.

Keywords

Intuitionistic logicmodal logictense logicmonadic quantifiersGödel translation

MSC classification

Primary: 03B44: Temporal logic
Secondary: 03B45: Modal logic (including the logic of norms) 03B55: Intermediate logics
Type
Research Article
Information
The Review of Symbolic Logic , Volume 16 , Issue 1 , March 2023 , pp. 164 - 187
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Bass, H. (1958). Finite monadic algebras. Proceedings of the American Mathematical Society, 9, 258–268.CrossRefGoogle Scholar
Bezhanishvili, G. (1998). Varieties of monadic Heyting algebras. I. Studia Logica, 61(3), 367–402.CrossRefGoogle Scholar
Bezhanishvili, G. (1999). Varieties of monadic Heyting algebras. II. Duality theory. Studia Logica, 62(1), 21–48.CrossRefGoogle Scholar
Bezhanishvili, G., & Carai, L. (2020). Temporal interpretation of intuitionistic quantifiers . In Olivetti, N., Verbrugge, R., Negri, S., and Sandu, S., editors. Advances in Modal Logic, Vol. 13. London: College Publications, pp. 95–114.Google Scholar
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal Logic. Cambridge Tracts in Theoretical Computer Science, Vol. 53. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Blok, W. J. (1976). Varieties of Interior Algebras. Ph.D. Thesis, University of Amsterdam.Google Scholar
Bull, R. A. (1965). A modal extension of intuitionist logic. Notre Dame Journal of Formal Logic, 6(2), 142–146.CrossRefGoogle Scholar
Bull, R. A. (1966). MIPC as the formalisation of an intuitionist concept of modality. The Journal of Symbolic Logic, 31(4), 609–616.CrossRefGoogle Scholar
Chagrov, A., & Zakharyaschev, M. (1997). Modal Logic. New York: Oxford University Press.Google Scholar
Esakia, L. (1975). The problem of dualism in the intuitionistic logic and Browerian lattices. V Inter. Congress of Logic, Methodology and Philosophy of Science, pp. 7–8.Google Scholar
Esakia, L. (1978). Semantical analysis of bimodal (tense) systems. Logic, Semantics and Methodology . Tbilisi: Metsniereba Press, pp. 87–99 (in Russian).Google Scholar
Esakia, L. (1988). Provability logic with quantifier modalities. Intensional Logics and Logical Structure of Theories. Tbilisi: Metsniereba Press, pp. 4–9 (in Russian).Google Scholar
Esakia, L. (2019). Heyting Algebras: Duality Theory . Trends in Logic—Studia Logica Library, Vol. 50. Cham: Springer. Edited by Guram Bezhanishvili and Wesley H. Holliday, Translated from the Russian edition by Anton Evseev.CrossRefGoogle Scholar
Fischer-Servi, G. (1977). On modal logic with an intuitionistic base. Studia Logica, 36(3), 141–149.CrossRefGoogle Scholar
Fischer-Servi, G. (1978). The finite model property for MIPQ and some consequences. Notre Dame Journal of Formal Logic, 19(4), 687–692.CrossRefGoogle Scholar
Gabbay, D. M., Kurucz, A., Wolter, F., & Zakharyaschev, M. (2003). Many-Dimensional Modal Logics: Theory and Applications . Amsterdam: North-Holland.Google Scholar
Gabbay, D. M., & Shehtman, V. B. (1998). Products of modal logics. I. Logic Journal of IGPL, 6(1), 73–146.CrossRefGoogle Scholar
Goldblatt, R. (1992). Logics of Time and Computation (second edition). CSLI Lecture Notes, Vol. 7. Stanford: Center for the Study of Language and Information, Stanford University.Google Scholar
Grefe, C. (1998). Fischer Servi’s intuitionistic modal logic has the finite model property. In Kracht, M., de Rijke, M., Wansing, H., and Zakharyaschev, M., editors. Advances in Modal Logic (Berlin, 1996), Vol. 1. CSLI Lecture Notes, 87. Stanford: CSLI Publications, pp. 85–98.Google Scholar
Halmos, P. R. (1956). Algebraic logic. I. Monadic Boolean algebras. Compositio Mathematica, 12, 217–249.Google Scholar
Jónsson, B., & Tarski, A. (1951). Boolean algebras with operators. I. American Journal of Mathematics, 73, 891–939.CrossRefGoogle Scholar
McKinsey, J. C. C., & Tarski, A. (1944). The algebra of topology. Annals of Mathematics. Second Series, 45, 141–191.CrossRefGoogle Scholar
Ono, H. (1977). On some intuitionistic modal logics. Publications of the Research Institute for Mathematical Sciences, 13(3), 687–722.CrossRefGoogle Scholar
Ono, H. (1987). Some problems in intermediate predicate logics. Reports on Mathematical Logic, 21, 55–67.Google Scholar
Ono, H., & Suzuki, N.-Y. (1988). Relations between intuitionistic modal logics and intermediate predicate logics. Reports on Mathematical Logic, 22, 65–87 (1989).Google Scholar
Prior, A. N. (1957). Time and Modality. Oxford: Clarendon Press.Google Scholar
Rasiowa, H., & Sikorski, R. (1963). The Mathematics of Metamathematics. Warsaw: Państwowe Wydawnictwo Naukowe.Google Scholar
Rauszer, C. (1973/74). Semi-Boolean algebras and their applications to intuitionistic logic with dual operations. Fundamenta Mathematicae, 83(3), 219–249.CrossRefGoogle Scholar
Segerberg, K. (1970). Modal logics with linear alternative relations. Theoria, 36, 301–322.CrossRefGoogle Scholar
Thomason, S. K. (1972). Semantic analysis of tense logics. The Journal of Symbolic Logic, 37, 150–158.CrossRefGoogle Scholar
Wolter, F. (1998). On logics with coimplication. Journal of Philosophical Logic, 27(4), 353–387.CrossRefGoogle Scholar