No CrossRef data available.
Article contents
TABULARITY AND POST-COMPLETENESS IN TENSE LOGIC
Part of:
General logic
Published online by Cambridge University Press: 07 April 2022
Abstract
A new characterization of tabularity in tense logic is established, namely, a tense logic L is tabular if and only if 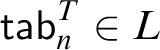 $\mathsf {tab}_n^T\in L$ for some
$\mathsf {tab}_n^T\in L$ for some 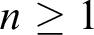 $n\geq 1$. Two characterization theorems for the Post-completeness in tabular tense logics are given. Furthermore, a characterization of the Post-completeness in the lattice of all tense logics is established. Post numbers of some tense logics are shown.
$n\geq 1$. Two characterization theorems for the Post-completeness in tabular tense logics are given. Furthermore, a characterization of the Post-completeness in the lattice of all tense logics is established. Post numbers of some tense logics are shown.
MSC classification
Primary:
03B44: Temporal logic
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
BIBLIOGRAPHY
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal Logic. New York: Cambridge University Press.CrossRefGoogle Scholar
Blok, W. (1980). Pretabular varieties of modal algebras. Studia Logica, 39, 101–124.CrossRefGoogle Scholar
Chagrov, A. & Shehtman, V. (1995). Algorithmic aspects of propositional tense logics. In Pacholski, L. and Tiuryn, J., editors. Computer Science Logic. Berlin–Heidelberg: Springer, pp. 442–455.CrossRefGoogle Scholar
Chagrov, A. & Zakharyaschev, M. (1997). Modal Logic. New York: Oxford University Press.CrossRefGoogle Scholar
Fritz, P. (2016). Post completeness in congruential modal logics. In Beklemishev, L., Demri, S., and Máté, A., editors. Advances in Modal Logic, Vol. 11. London: College Publications, pp. 288–301.Google Scholar
Kracht, M. (1992). Even more about the lattice of tense logics. Archive for Mathematical Logic, 31(4), 243–257.CrossRefGoogle Scholar
Ma, M. & Chen, Q. (2021). Lattices of finitely alternative normal tense logics. Studia Logica, 109, 1093–1118.CrossRefGoogle Scholar
Makinson, D. (1971). Some embedding theorems for modal logic. Notre Dame Journal of Formal Logic, 12(2), 252–254.CrossRefGoogle Scholar
Makinson, D. & Segerberg, K. (1974). Post completeness and ultrafilters. Mathematical Logic Quarterly, 20(25–27), 385–388.CrossRefGoogle Scholar
Maksimova, L. (1975). Pretabular extensions of Lewis S4. Algebra and Logic, 14, 16–33.CrossRefGoogle Scholar
Rautenberg, W. (1979). More about the lattice of tense logic. Bulletin of the Section of Logic, 8, 21–25.Google Scholar
Segerberg, K. (1972). Post completeness in modal logic. Journal of Symbolic Logic, 37(4), 711–715.CrossRefGoogle Scholar
Segerberg, K. (1976). The truth about some Post numbers. Journal of Symbolic Logic, 41(1), 239–244.CrossRefGoogle Scholar
Thomason, S. K. (1972). Semantical analysis of tense logic. Journal of Symbolic Logic, 37(1), 150–158.CrossRefGoogle Scholar
Wolter, F. (1995). The finite model property in tense logic. Journal of Symbolic Logic, 60(3), 757–774.CrossRefGoogle Scholar
Wolter, F. (1996). A counterexample in tense logic.
Notre Dame Journal of Formal Logic, 37(2), 167–173.CrossRefGoogle Scholar
Wolter, F. (1996). Properties of tense logics. Mathematical Logic Quarterly, 42, 481–500.CrossRefGoogle Scholar
Wolter, F. (1996). Tense logic without tense operators. Mathematical Logic Quarterly, 42, 145–171.CrossRefGoogle Scholar
Wolter, F. (1997). Completeness and decidability of tense logics closely related to logics above K4. Journal of Symbolic Logic, 62, 131–159.CrossRefGoogle Scholar
Wolter, F. (1997). The structure of lattices of subframe logics. Annals of Pure and Applied Logic, 86(13), 47–100.CrossRefGoogle Scholar
Wolter, F. & Zakharyaschev, M. (2007). Modal decision problems. In Blackburn, P., van Benthem, J., and Wolter, F., editors. Handbook of Modal Logic. Amsterdam: Elsevier, pp. 427–489.CrossRefGoogle Scholar
Zakharyaschev, M., Wolter, F., & Chagrov, A. (2001). Advanced modal logic. In Gabbay, D., and Guenthner, F., editors. Handbook of Philosophical Logic, Vol. 3. Dordrecht: Kluwer Academic, pp. 83–266.CrossRefGoogle Scholar


