1. Introduction
In two recent papers Berto [Reference Berto8, Reference Berto9] suggested semantics for reports of imagination episodes phrased as “‘It is imagined in the act whose explicit input is A, that B’ or more tersely, ‘It is imagined in act A that B’.”Footnote
1
The explicitness of the input here is to be understood as consisting of a deliberate choice by the single agent under consideration to imagine that A. The semantics in Berto [Reference Berto9] takes the semantics of counterfactual conditionals “If A were the case, then B would be the case”, written as
![]() $[A]B$
, as presented, for example, in Priest [Reference Priest52, chap. 7], and adds to the evaluation clause for conditionals
$[A]B$
, as presented, for example, in Priest [Reference Priest52, chap. 7], and adds to the evaluation clause for conditionals
![]() $[A]B$
a content filter requiring that the content of B be contained in the content of A, where “[c]ontents are the situations intentional acts of imagination are about.”
$[A]B$
a content filter requiring that the content of B be contained in the content of A, where “[c]ontents are the situations intentional acts of imagination are about.”
The reading of
![]() $[A]B$
as “It is imagined in the act whose explicit input is A, that B” is conceptually very loaded if one takes into account that in conditional logic
$[A]B$
as “It is imagined in the act whose explicit input is A, that B” is conceptually very loaded if one takes into account that in conditional logic
![]() $[A]B$
is read as “If A were the case, then B would be the case.” If the semantics of conditional logic captures the meaning of counterfactual conditionals, it is not at all obvious that the very same semantics also captures the truth conditions of imagination episode reports. Indeed, Berto does not just copy the semantics of counterfactual conditionals. The distinctive feature to capture imagination in Berto’s logic of imagination episode reports consists of either admitting non-normal possible words, as in Berto [Reference Berto8], or making use of a content filter, as in Berto [Reference Berto9].Footnote
2
$[A]B$
is read as “If A were the case, then B would be the case.” If the semantics of conditional logic captures the meaning of counterfactual conditionals, it is not at all obvious that the very same semantics also captures the truth conditions of imagination episode reports. Indeed, Berto does not just copy the semantics of counterfactual conditionals. The distinctive feature to capture imagination in Berto’s logic of imagination episode reports consists of either admitting non-normal possible words, as in Berto [Reference Berto8], or making use of a content filter, as in Berto [Reference Berto9].Footnote
2
Upon comparison of Berto’s logic of imagination episode reports with the stit-imagination logic from Olkhovikov and Wansing [Reference Olkhovikov and Wansing48, Reference Olkhovikov and Wansing49] and Wansing [Reference Wansing67], it becomes clear that the two approaches can be combined in a mutually supplementary way. Whereas Berto focuses on the episodic character of imagination, in stit-imagination logic the focus is on the agentive aspect of imagination, and it seems to be quite natural to represent these two features of imagination in a combined framework. In a multi-agent setting, one would then use the unary imagination operators
![]() $I_a$
from stit-imagination logics (where
$I_a$
from stit-imagination logics (where
![]() $I_a$
is read as “agent a (actively) imagines that”) together with binary imagination episode operators
$I_a$
is read as “agent a (actively) imagines that”) together with binary imagination episode operators
![]() $[a]\!\!\!\rightarrow \!\,$
, where
$[a]\!\!\!\rightarrow \!\,$
, where
![]() $A[a]\!\!\!\rightarrow \! B$
is read as “agent a’s actively imagining that A results in a’s mental image containing the proposition expressed by B.”Footnote
3
The imagination operator of stit-imagination logic is an operator that merges the dstit (deliberatively seeing-to-it-that) operator from stit-theory [Reference Belnap, Perloff and Xu6] with a weak congruential modal operator that is interpreted in a neighborhood semantics [Reference Pacuit50]. The latter component models the propositional contents of imagination, and the semantics of stit-imagination logic thereby has the resources to capture a non-agentive notion of imagination content as resulting from a deliberate act of imagination. The suggested episodic operator
$A[a]\!\!\!\rightarrow \! B$
is read as “agent a’s actively imagining that A results in a’s mental image containing the proposition expressed by B.”Footnote
3
The imagination operator of stit-imagination logic is an operator that merges the dstit (deliberatively seeing-to-it-that) operator from stit-theory [Reference Belnap, Perloff and Xu6] with a weak congruential modal operator that is interpreted in a neighborhood semantics [Reference Pacuit50]. The latter component models the propositional contents of imagination, and the semantics of stit-imagination logic thereby has the resources to capture a non-agentive notion of imagination content as resulting from a deliberate act of imagination. The suggested episodic operator
![]() $[a]\!\!\!\rightarrow \!$
is definable when a content-sensitive conditional operator
$[a]\!\!\!\rightarrow \!$
is definable when a content-sensitive conditional operator
![]() is added to stit-imagination logic. The combined approaches lead to a semantics that (in)validates analogues of the desired (in)validities from Berto [Reference Berto9]. The semantics improves on Berto’s approach in the following ways: (i) it explicitly models the agent’s deliberate choice of the initial input of an imaginative episode, (ii) in a multi-agent setting, (iii) provides a purely structural correspondence theory due to employing Chellas–Segerberg semantics for the conditional operator [Reference Chellas20, Reference Chellas21, Reference Segerberg57, Reference Unterhuber62, Reference Unterhuber and Schurz63, Reference Wansing and Unterhuber68], which in turn (iv) provides the possibility of dropping some potentially debatable axioms.
is added to stit-imagination logic. The combined approaches lead to a semantics that (in)validates analogues of the desired (in)validities from Berto [Reference Berto9]. The semantics improves on Berto’s approach in the following ways: (i) it explicitly models the agent’s deliberate choice of the initial input of an imaginative episode, (ii) in a multi-agent setting, (iii) provides a purely structural correspondence theory due to employing Chellas–Segerberg semantics for the conditional operator [Reference Chellas20, Reference Chellas21, Reference Segerberg57, Reference Unterhuber62, Reference Unterhuber and Schurz63, Reference Wansing and Unterhuber68], which in turn (iv) provides the possibility of dropping some potentially debatable axioms.
Why are each of these improvements philosophically warranted? First, in modelling the agent’s deliberate choice of the initial input, we can not only model that an agent chooses to imagine something but also whether an agent chooses not to imagine something. This can be seen as an unwillingness on the agent’s part to imagine that content—they won’t imagine that content. This is an important aspect appealed to in so-called “wontian” theories to solve the problem of imaginative resistance. This problem is, roughly, that often we fail to imagine something, although we are asked to imagine it.Footnote 4 Wontian theories hold that agents simply won’t (and don’t want to) imagine certain contents. Cantian (can’t-ian) theories hold that an agent simply cannot imagine certain contents because they are impossible to be represented as true [Reference Tuna and Zalta61]. Also this can be modelled in our framework with another modality.
Second, what about the modularity we get with a correspondence theory? As Berto points out, some of his principles might fall prey to counterexamples. We discuss various principles and argue that the philosophical literature is not decisive about all of them. Hence, a framework that allows modelling differing assumptions about the logic of imagination is desirable.Footnote 5
Here is a plan of the paper. In Section 2, we shall assort a conception of imagination as episodic, which is quite popular in the literature on imagination, and which has been spelled out to varying extent, see, e.g., [Reference Dorsch27, Reference Langland-Hassan, Kind and Kung40, Reference Nichols and Stich46, Reference Williamson, Kind and Kung71]. We also introduce some issues pertaining to logical closure properties. This presentation is intended to substantiate the development of the kind of imagination modalities we are about to introduce. In Section 3, we rehearse Berto’s semantics and briefly discuss the core (in)validities concerning imagination. Section 4 is devoted to semantically defining a logic of imagination episodes as indicated in our introductory remarks. Thereafter, in Section 5, we establish frame correspondences. We discuss the significance of our results compared to Berto’s semantics, and also briefly compare our semantics to some recent work [Reference Canavotto, Giordani and Berto15] in Section 6. An in-depth comparison of our approach with [Reference Canavotto, Giordani and Berto15] is beyond the scope of this paper. As an outlook for such further studies, we identify four aspects in which their and our approach differ and which call for further investigation: flexibility to incorporate or disregard (un)desirable (in)validities, the notion of deliberate choice of imagined content, the philosophical interpretation of the formalism, the suitability for modelling the temporal expansion of imaginative episodes. Finally, in Section 7 we conclude by summarising our results and discussion.
2. Episodic imagination with voluntary input
The contents of our imaginings seem to be subject to our will [Reference Dorsch27, Reference Kind, Kung, Kind and Kung37]. Setting aside the debate concerning some extreme cases like impossibilities, see, e.g., [Reference Berto and Schoonen12, Reference Priest53], we can imagine whatever we like.
On the other hand, imagination is a source of justified belief, and sometimes even knowledge. In the epistemology of conditionals, the suppositional heuristic, inspired by the so-called Ramsey test,Footnote 6 is sometimes explicated in terms of imagination, for example, by Williamson [Reference Williamson70, pp. 152–153]:
There is no uniform epistemology of counterfactual conditionals. In particular, imaginative simulation is neither always necessary nor always sufficient for their evaluation, even when they can be evaluated. Nevertheless, it is the most distinctive cognitive feature of the process of evaluating them [
![]() $\ldots $
] [O]ne supposes the antecedent and develops the supposition, adding further judgments within the supposition by reasoning, offline predictive mechanisms, and other offline judgments. [
$\ldots $
] [O]ne supposes the antecedent and develops the supposition, adding further judgments within the supposition by reasoning, offline predictive mechanisms, and other offline judgments. [
![]() $\ldots $
] To a first approximation: one asserts the counterfactual conditional if and only if the development [of the antecedent] eventually leads one to add the consequent.
$\ldots $
] To a first approximation: one asserts the counterfactual conditional if and only if the development [of the antecedent] eventually leads one to add the consequent.
One starts out supposing the antecedent, which is then unfolded in the imagination, until one either accepts the consequent, given the supposition and its unfolding, or rejects it, given the supposition and its unfolding. This development is not unconstrained [Reference Kind, Kind and Kung34, Reference Langland-Hassan, Kind and Kung40, Reference Nichols and Stich46]. For example, it follows some logical rules, and it takes into account relevance considerations by being reality-oriented [Reference Berto, Verdée and Andreas7, Reference Berto10, Reference Byrne14, Reference Casas-Roma, Huertas and Rodríguez17, Reference Casas-Roma, Rodríguez and Huertas18, Reference Kind, Kind and Kung34, Reference Williamson, Kind and Kung71].
Of course, imagining agents are always free to intervene and introduce new contents at will, thereby generating an imaginative sub-episode [Reference Dorsch27, Reference Langland-Hassan, Kind and Kung40]. This is again the feature that imagination is, in some sense, “up to us” [Reference Kind, Kung, Kind and Kung37]. In what follows, when we speak of “chosen contents” of an imaginative episode with voluntary input, we mean either the initial input or a content given by such an intervention.
These features suggest that there is a philosophically useful notion of imaginative episodes, which is composed of imaginative states in the following way: the content of the initial state is deliberately chosen, while the subsequent contents are either again deliberately chosen (thereby generating a new sub-episode), or the content is developed from some previous content(s) according to some constraints [Reference Langland-Hassan39]. We call the former the deliberate content and the latter the unfolded content. And indeed, in recent work, starting with [Reference Nichols and Stich46], several authors [Reference Berto9, Reference Kung38, Reference Langland-Hassan, Kind and Kung40] have combined these two features of imagination into one of imaginative episodes with voluntary input. To a varying extent, this notion is appealed to in various areas of philosophy to explain phenomena such as pretence [Reference Walton64], understanding other minds [Reference Currie and Ravenscroft25, Reference Nichols and Stich46], counterfactual thinking [Reference Byrne14, Reference Williamson70], and our beliefs in/knowledge of modal claims [Reference Chalmers, Gendler and Hawthorne19, Reference Kung38, Reference Williamson70, Reference Yablo72]. Uses of imagination that have this explanatory power, and which even feature in our everyday lives in planning and decision-making have recently been labelled “reality-oriented mental simulation” (ROMS) [Reference Berto9], “instructive uses of imagination” [Reference Kind and Kung36], and “epistemically useful imagination” [Reference Badura and Kind3]. All these labels have in common that they emphasise that imagination can be used to gain justified beliefs about the world and what it could be like. We use them interchangably. It is this notion we are targeting in the present paper and we are aiming to better understand qua formalisation. In the present approach, we presuppose certain philosophical insights, most importantly that epistemically useful imaginative episodes obey certain constraints, shared by authors such as those of [Reference Badura, Badura and Kind1, Reference Casas-Roma, Huertas and Rodriguez16, Reference Kind, Kind and Kung34, Reference Langland-Hassan, Kind and Kung40, Reference Williamson, Kind and Kung71].
While Berto has provided first steps towards modelling this notion, his focus has been the connection between initial and unfolded content in the single agent case. We aim to model the deliberate choice of an agent during an imaginative episode and the subsequent unfolding. To account for the deliberate choice, we employ the stit-imagination operator from [Reference Olkhovikov and Wansing48, Reference Olkhovikov and Wansing49, Reference Wansing67], which we don’t take as primitive but defined by a stit-modality and a neighborhood modality. The unfolding is modelled by a content-sensitive variably strict conditional as per Berto’s imaginative episode operator. The formal advantages over existing logics for imagination have been hinted at in the introduction and will be shown later on.
Since the semantics will already be quite involved (although it features mostly standard modalities), we ignore the modelling of background knowledge/belief, and the temporal development of imaginative episodes. Agents also might have some question in mind, which they would like to answer with their imaginative episode [Reference Canavotto, Giordani and Berto15]. Taking this into account would require modelling imaginative projects, of which imaginative episodes are parts. We leave this aspect for future work.
Before presenting the formal semantics, a brief note of caution: we are intending to model conscious imaginative episodes. That is, we focus on (that part of) imaginative episodes in which the agent is conscious of what they are imagining, regardless of whether it is something voluntarily imagined or has unfolded from a previous imagining. We leave open the possibility that there might be imaginative episodes in which we are not conscious of what we are imagining (dreams might be seen as one example, although not everyone considers dreams to be imaginative episodes). Why this focus? If we asked someone what they were imagining, they would usually only be able to express those imaginings they are conscious of.
2.1. Logical omni-imagination and hyperintensionality
As mentioned, the unfolding of the chosen contents is constrained in certain ways. One such constraint is in terms of logical consequence, which can be phrased descriptively or normatively: one imagines (may imagine) p iff p follows by some logic, usually classical logic, from some chosen input. So, all and only logical consequences of chosen inputs are imagined (or may be imagined). Clearly, this constraint applies only to propositional imagination, that is, imaginative episodes with propositional content, and which are usually phrased by “a imagines that p.” Both directions are too strong, even if one only considers propositional imagination. We do not only imagine classical logical consequences of chosen inputs, and also it’s not the case that we may imagine only the classical logical consequences of chosen inputs. Also, we (may) imagine contents that are, in some sense, merely associated with the chosen ones. For example, when I imagine that I am at the beach, I imagine that I am wearing sunglasses. Assume that I have some background beliefs that feature here, for instance, that if one is at the beach, usually, one wears sunglasses. This background belief is best not modelled as a material implication but as a default-conditional. These are studied in non-monotonic (and thus non-classical) logic [Reference Straßer, Antonelli and Zalta59]. Thus, my imagination features consequences that don’t follow by classical propositional or predicate logic.
Moreover, we do not imagine all classical consequences of the chosen inputs, and it is not the case that we may imagine all classical consequences of the chosen inputs. Sometimes, it is even impermissible to do so, especially in multi-agent scenarios. For example, if one is playing a game of Dungeons & Dragons, which has a fantasy medieval setting, it is impermissible to imagine that one is carrying a lightsaber or that one is not carrying a lightsaber. One’s imagination mustn’t be about lightsabers.
It is even inadequate to assume that we do imagine all classical consequences of the chosen inputs. This is the problem of logical omni-imagination (and non-imagination), which is just the imagination-variant of the problem of logical omniscience (and ignorance). Informally speaking, this problem takes the following forms (the first four correspond to Om1–Om4 in Wansing [Reference Wansing67]), where I is a placeholder for “it is imagined that” or “the agent imagines that” and
![]() $\supset $
is material implication:
$\supset $
is material implication:
-
Imagination of all Valid Formulas (IVF) if A is valid, then
 $I A$
is valid.
$I A$
is valid. -
No Imagination of Unsatisfiable Formulas (NIUF) if A is unsatisfiable, then
 $I A$
is unsatisfiable.
$I A$
is unsatisfiable. -
Closure under Valid Implication (CVI) if
 $A\supset B$
is valid, then
$A\supset B$
is valid, then
 $IA \supset IB$
is valid.
$IA \supset IB$
is valid. -
Closure of imagination under Valid (material) Equivalence (CVE) if
 $A\equiv B$
is valid, then
$A\equiv B$
is valid, then
 $IA\equiv IB$
is valid.
$IA\equiv IB$
is valid. -
Closure of imagination under Imagined Implication (CII)
 $I A, I(A\supset B)\models IB$
.
$I A, I(A\supset B)\models IB$
.
Given we are considering a stage in an imaginative episode, we have two ways of understanding I and “it is imagined that.” First, as “it is deliberately imagined that” or, second, as “it is involuntarily imagined that,” by which we intend to mean that the agent’s imagined content somehow “unfolds” from something previously imagined.
It is clear that IVF and NIUF ignore the notion of deliberate choice. That is, if one understands I in IVF and NIUF as “the agent deliberately imagines that,” they are implausible. The reason that one imagines or does not imagine, respectively, the respective content is because it is a tautology or is unsatisfiable. The agent’s choices play no role whatsoever.
In CVI, it is assumed that
![]() $A\supset B$
is valid. Now, even if the agent deliberately imagines that A, they do not seem to deliberately imagine that B. Consider the valid implication
$A\supset B$
is valid. Now, even if the agent deliberately imagines that A, they do not seem to deliberately imagine that B. Consider the valid implication
![]() $p\supset (q\supset p)$
. If one deliberately imagines that one is having cake, one doesn’t deliberately imagine that if Trump wins the election, then one is having cake. One is not concerned with a scenario in which one eats cake if something happens but rather with a scenario in which one is having cake. At best, the deliberate imagining that A “unfolds” to a non-deliberate, or involuntary, imagining that B. In the example, one’s imagining that one is having cake could then “unfold” by valid implication to imagining that if Trump wins the election, then one is having cake. Below, we argue that initial deliberate imaginings often are not unfolded to everything that is validly implied by it. That is, even if one reads the second occurrence of “I” in CVI as “it is involuntarily imagined that,” CVI shouldn’t hold.
$p\supset (q\supset p)$
. If one deliberately imagines that one is having cake, one doesn’t deliberately imagine that if Trump wins the election, then one is having cake. One is not concerned with a scenario in which one eats cake if something happens but rather with a scenario in which one is having cake. At best, the deliberate imagining that A “unfolds” to a non-deliberate, or involuntary, imagining that B. In the example, one’s imagining that one is having cake could then “unfold” by valid implication to imagining that if Trump wins the election, then one is having cake. Below, we argue that initial deliberate imaginings often are not unfolded to everything that is validly implied by it. That is, even if one reads the second occurrence of “I” in CVI as “it is involuntarily imagined that,” CVI shouldn’t hold.
So, let us consider the case in which I is understood as “the agent imagines involuntarily.” There are various examples to show that IVF-CVE should not hold.
As for IVF, consider a case of reality-oriented imagination, in which one voluntarily imagines that one is at the beach for vacation. In voluntarily imagining that one is at the beach for vacation, one typically does not involuntarily imagine an arbitrary tautology. In other words, that one is at the beach typically does not unfold to an arbitrary tautology. In imagining about one’s vacation, one doesn’t introduce arbitrary validities, such as “If Trump wears a tutu, then Trump wears something.” One’s conscious imagining simply isn’t about Trump.Footnote 7
A more damning example is the “drinker paradox” from first-order logic. The formula
![]() $\exists x(Dx\supset \forall y Dy)$
is valid in classical first-order logic. So, if IVF was the case, agents would (consciously) imagine this for arbitrary predicates. Hence, they make their imagination about some arbitrary predicate D. This is hardly correct. Consider, again, the case of planning one’s vacation. According to IVF and in combination with the drinker-sentence, one would (consciously) imagine that there is something such that if it is programmed in C, then everything is programmed in C. Again, our imagination is not about things that are programmed in C. It would even be “inappropriate” or “impermissible” to imagine that there is something such that if it is programmed in C, then everything is programmed in C. Let us elaborate this idea of being inappropriate/impermissible with respect to the idea from the introduction that (epistemically useful) imaginative episodes obey certain constraints. Given that one is planning one’s vacation, and that an imaginative episode in such a setting is subject to several constraints—among them a relevance constraint [Reference Badura, Badura and Kind1, Reference Kind, Kind and Kung34]—it is “inappropriate” or “impermissible” with respect to these constraints (or rules) to imagine about the predicate D for it is irrelevant. Compare the case above concerning imagining about lightsabers in the context of a game of Dungeons & Dragons. Imaginative episodes are structurally much like games of pretence or make-believe—which have been extensively discussed by Walton [Reference Walton64]—in that they obey certain rules but their rules can differ with respect to the context the game is played in. Imaginative episodes involved in planning or decision-making—that is, imaginative episodes that have been given as examples of instructive uses of imagination—are much more constrained than what have been called “transcendent uses of imagination” [Reference Kind and Kung36]. So, while one certainly can imagine whatever one wants, even in these contexts, it might be impermissible to do so given the relevance constraints.
$\exists x(Dx\supset \forall y Dy)$
is valid in classical first-order logic. So, if IVF was the case, agents would (consciously) imagine this for arbitrary predicates. Hence, they make their imagination about some arbitrary predicate D. This is hardly correct. Consider, again, the case of planning one’s vacation. According to IVF and in combination with the drinker-sentence, one would (consciously) imagine that there is something such that if it is programmed in C, then everything is programmed in C. Again, our imagination is not about things that are programmed in C. It would even be “inappropriate” or “impermissible” to imagine that there is something such that if it is programmed in C, then everything is programmed in C. Let us elaborate this idea of being inappropriate/impermissible with respect to the idea from the introduction that (epistemically useful) imaginative episodes obey certain constraints. Given that one is planning one’s vacation, and that an imaginative episode in such a setting is subject to several constraints—among them a relevance constraint [Reference Badura, Badura and Kind1, Reference Kind, Kind and Kung34]—it is “inappropriate” or “impermissible” with respect to these constraints (or rules) to imagine about the predicate D for it is irrelevant. Compare the case above concerning imagining about lightsabers in the context of a game of Dungeons & Dragons. Imaginative episodes are structurally much like games of pretence or make-believe—which have been extensively discussed by Walton [Reference Walton64]—in that they obey certain rules but their rules can differ with respect to the context the game is played in. Imaginative episodes involved in planning or decision-making—that is, imaginative episodes that have been given as examples of instructive uses of imagination—are much more constrained than what have been called “transcendent uses of imagination” [Reference Kind and Kung36]. So, while one certainly can imagine whatever one wants, even in these contexts, it might be impermissible to do so given the relevance constraints.
A similar case can be made for CVI.Footnote
8
There might be an insufficient connection in terms of content or relevance between A and B. So, while one might entail the other, imagining one might not entail imagining the other. If in CVI, B is a tautology, the same argument from before applies. But even for simple cases, CVI seems problematic. The implication
![]() $\forall x(Fx\supset Gx) \supset (Fa \supset Ga)$
is valid for any a, F and G. But one’s imagination might not be concerned with a at all or it might be that a is irrelevant for one’s imagining. For example, consider a situation in which one is playing a game and imagines that all one’s opponents (say, Donald, Kim, and Angela) are cheating. So, it is the case that for all x, if x is my opponent, then x is cheating. Sure, this is also true for myself, i.e., “if I am my opponent, then I am cheating” but why would I imagine that in our game? Or, alternatively, pick any other individual, say, Vladimir. If he’s not part of our game, the implication “If Vladimir is my opponent, then he’s cheating” is irrelevant for my thoughts about the game, which has only the four players mentioned. Another example can be given by
$\forall x(Fx\supset Gx) \supset (Fa \supset Ga)$
is valid for any a, F and G. But one’s imagination might not be concerned with a at all or it might be that a is irrelevant for one’s imagining. For example, consider a situation in which one is playing a game and imagines that all one’s opponents (say, Donald, Kim, and Angela) are cheating. So, it is the case that for all x, if x is my opponent, then x is cheating. Sure, this is also true for myself, i.e., “if I am my opponent, then I am cheating” but why would I imagine that in our game? Or, alternatively, pick any other individual, say, Vladimir. If he’s not part of our game, the implication “If Vladimir is my opponent, then he’s cheating” is irrelevant for my thoughts about the game, which has only the four players mentioned. Another example can be given by
![]() $p\supset (q\supset p)$
. Suppose I imagine that I am eating icecream. According to IVF and this axiom, I would also imagine that if I am on Mars, then I eat icecream. This is hardly correct, unless one’s imagination is already concerned with being on Mars. Imagination, especially if reality-oriented, is highly sensitive concerning relevant content.Footnote
9
$p\supset (q\supset p)$
. Suppose I imagine that I am eating icecream. According to IVF and this axiom, I would also imagine that if I am on Mars, then I eat icecream. This is hardly correct, unless one’s imagination is already concerned with being on Mars. Imagination, especially if reality-oriented, is highly sensitive concerning relevant content.Footnote
9
As for NIUF, sometimes, imagining classically unsatisfiable sentences might be necessary to understand certain works of art. For example, Graham Priest’s story Sylvan’s Box [Reference Priest51] features a box that is empty and has something in it. Assume it’s true in the story that there is an empty box that also has something in it. Priest (or his fictional analogue) and his colleague go on to bury the box and put it into the trunk, at the same time. Assume also that this is true in the story. It seems, to understand why the latter is true in the story requires one to understand that the former is true in the story. If one follows [Reference Walton64] in that what’s true in a story is just what we ought to imagine, as many do in the literature on fiction, then it seems that we ought to imagine at least one contradiction. And since “ought” implies “can,” we can imagine contradictions. If imagining contradictions is granted, it makes a lot of sense to be able to semantically distinguish between different formulas that are all classically unsatisfiable. If one imagines that Sylvan’s box is both empty and not empty, this should not entail that one imagines that Donald Trump (simultaneously) does and does not wear a tutu. Logical non-imagination as expressed by NIUF can then be avoided by working with a paraconsistent logic using a semantics that allows for truth-value gluts or states that for some formulas may at the same time support their truth and support their falsity.Footnote 10 As has been pointed out in the discussion of logical omniscience in epistemic logic, the use of a paraconsistent non-modal base logic, however, does not necessarily avoid logical omniscience as stated by analogues of IVF, Om 3, and CVE, cf. [Reference Fagin and Halpern29].
Of course, one person’s modus ponens is another’s modus tollens. So, instead, one could claim that it’s not true in the story that there is such a box because we can’t imagine contradictions, and so we can’t be obliged to imagine the contradiction. But not only theories of truth in fiction might require that we can imagine contradictions (or, more generally, impossibilities). For example, if imagination is meant to do the explanatory work in, say, modal epistemology, it is necessary that we can imagine contradictions. For accounts by Yablo [Reference Yablo72], Chalmers [Reference Chalmers, Gendler and Hawthorne19], and Williamson [Reference Williamson70] all ultimately require that p is possible in case imagining it does not lead to imagining a contradiction.Footnote 11 And, more importantly, at least Williamson holds that p is impossible if imagining it leads to imagining a contradiction. Thus, impossibility is explained in terms of imagining a contradiction. Moreover, in Williamson’s approach, p is necessary if imagining its negation leads to imagining a contradiction. So, the semantics one provides for imagination reports should at least be flexible enough so as to allow for the case of imagining contradictions. Ideally, some conditions can be added to or dropped from the semantics, depending on one’s stance on the possibility of imagining contradictions.
Let us now come back to CVE and the issue of hyperintensionality. Let L be a logic, let A, B, and C be L-formulas, and let
stand for mutual entailment in L. Moreover, let
![]() $C(A)$
be the result of uniformly substituting A for some atomic formula p in C, and
$C(A)$
be the result of uniformly substituting A for some atomic formula p in C, and
![]() $C(B)$
the result of uniformly substituting B for p in C. Then L is hyperintensional only if L is not selfextensional, i.e., only if the following inference is not validity preserving:Footnote
12
$C(B)$
the result of uniformly substituting B for p in C. Then L is hyperintensional only if L is not selfextensional, i.e., only if the following inference is not validity preserving:Footnote
12

Equivalently, the selfextensionality of L can be defined by requiring that for every n-place connective
![]() $\sharp $
, the following inference is admissible:
$\sharp $
, the following inference is admissible:

A connective
![]() $\sharp $
is congruential according to L if the above inference for it is admissible in L. So, if a logic satisfies CVE for its imagination operator (and all other connectives are congruential, too), it will not be hyperintensional. It has been pointed out by Wansing [Reference Wansing67] that the stit-imagination operator discussed therein satisfies CVE but not IVF-CVI (and not CII). It is thus not hyperintensional. We discuss hyperintensionality wrt Berto’s semantics in Section 3. Not being hyperintensional may be seen as problematic, as the following example shows:
$\sharp $
is congruential according to L if the above inference for it is admissible in L. So, if a logic satisfies CVE for its imagination operator (and all other connectives are congruential, too), it will not be hyperintensional. It has been pointed out by Wansing [Reference Wansing67] that the stit-imagination operator discussed therein satisfies CVE but not IVF-CVI (and not CII). It is thus not hyperintensional. We discuss hyperintensionality wrt Berto’s semantics in Section 3. Not being hyperintensional may be seen as problematic, as the following example shows:
-
(S) Batman catches Joker.
-
(S’) Bruce Wayne catches Joker.
Assuming “Batman” and “Bruce Wayne” are rigid designators, (S) and (S’) are logically equivalent. It is already arguable that believing (S) is equivalent to believing (S’), as is witnessed by the discussion on logical omniscience [Reference Fagin and Halpern29, Reference Jago32, Reference Rendsvig, Symons and Zalta55]. Why, then, should imagining (S) be equivalent to imagining (S’)? In fact, one might imagine (S) and also imagine that Harvey Dent is Batman, and thus imagine that Harvey Dent catches Joker. If one also imagines that Harvey and Bruce are not identical, one does not imagine that Bruce catches Joker.
If one grants that imagination does play a key role in engaging and appreciating fiction, as most authors do in the philosophy of fiction,Footnote 13 following Walton [Reference Walton64], then these types of mistakes of imagination are sometimes considered essential for engaging with works of fiction. Works of fiction mislead us in the beginning to make these types of mistakes. Then they surprise us later by revealing the identity of what we thought were two different characters. Often we appreciate works of fiction for this reason. It is odd to say that someone who mistakenly imagines Harvey to be Batman actually was imagining Bruce to be Batman just because they imagined Batman was catching Joker.
In [Reference Wansing67] an understanding of mental imagery as generated in acts of imagination is assumed that leads to an endorsement of CVE. Moreover, it is pointed out that in comparison to epistemic logic, where a distinction is drawn between implicit and explicit belief, and closure under valid equivalence is accepted for implicit belief (and knowledge), cf. [Reference Fagin and Halpern29], a distinction between implicit and explicit voluntary imagination seems to be less plausible. If we deal with imagination episodes with voluntary input, the implicit versus explicit distinction and with it the plausibility of CVE can be considered for both the voluntary input and the involuntary output of such episodes. We shall come back to this issue in our discussion of logical omni-imagination in Section 3.
What remains to consider is CII. And indeed, it seems to come closest to the idea of choosing an initial input A, incorporating some constraint,
![]() $I(A\supset B)$
, which then unfolds to imagining that B. In its formulation, however, there is an ambiguity as to what I, or “imagines that,” stands for. In the first premise, it seems to be understood as deliberate imagination, while in the conclusion it is imagining due to unfolding. Moreover, how it is used in the second premise, is not entirely clear. We won’t dwell on these details here because the formal semantics by Berto and our semantics will allow for precise formulations of IVF-CII, which are not subject to such ambiguities.
$I(A\supset B)$
, which then unfolds to imagining that B. In its formulation, however, there is an ambiguity as to what I, or “imagines that,” stands for. In the first premise, it seems to be understood as deliberate imagination, while in the conclusion it is imagining due to unfolding. Moreover, how it is used in the second premise, is not entirely clear. We won’t dwell on these details here because the formal semantics by Berto and our semantics will allow for precise formulations of IVF-CII, which are not subject to such ambiguities.
It must be mentioned, however, that CII might be objected to on grounds of bounded rationality for CII entails that agents can perform modus ponens arbitrarily many times within their imagination. Bounded rationality is “the conflict between normative principles of rationality and the fact that agents with which we are concerned have limited cognitive resources. It is a problem specifically for assigning contents to attitudes of rational but cognitively bounded agents, such as ourselves” [Reference Jago32, p. 165]. If CII is a norm of rationality and we consider actual agents, then, since these agents are cognitively bounded, they might fail to conform to the norm. They might not be able to perform modus ponens within their imagination arbitrarily many times. So if the aim is to model agents that are close to actual agents, which is Berto’s and also our aim, CII might also have to be dropped. As we will show, our semantics allows to invalidate the version of CII involving our episodic imagination operator, while the version of CII involving Berto’s imagination operator is valid in Berto’s semantics.
3. Berto’s semantics
For ease of reference, we review the central definitions and (in)validities from Berto’s logic [Reference Berto9] here. The language L contains a countable set of atomic formulas
![]() $Var=\lbrace p_i, q_i, r_i,\ldots \mid i\in \mathbb {N}\rbrace $
. We sometimes drop the index and use p, q, r as schematic atomic formulas. If A is a formula, by
$Var=\lbrace p_i, q_i, r_i,\ldots \mid i\in \mathbb {N}\rbrace $
. We sometimes drop the index and use p, q, r as schematic atomic formulas. If A is a formula, by
![]() $Var(A)$
we denote the set of atomic formulas occurring in A. The language L also contains the connectives
$Var(A)$
we denote the set of atomic formulas occurring in A. The language L also contains the connectives
![]() $\neg $
,
$\neg $
,
![]() $\wedge $
,
$\wedge $
,
![]() $\rightarrow $
; brackets
$\rightarrow $
; brackets
![]() $[,]$
and parentheses
$[,]$
and parentheses
![]() $(,)$
. We use
$(,)$
. We use
![]() $\Rightarrow $
to express material implication in the meta-language, and we use
$\Rightarrow $
to express material implication in the meta-language, and we use
![]() $\forall $
,
$\forall $
,
![]() $\exists $
to express universal and particular quantification in the meta-language, respectively.
$\exists $
to express universal and particular quantification in the meta-language, respectively.
Definition 3.1 (Formulas)
The set of formulas,
![]() $Form(L)$
, is given by the following Backus–Naur grammar:
$Form(L)$
, is given by the following Backus–Naur grammar:
where
![]() $p\in Var$
.
$p\in Var$
.
The intended reading is that
![]() $\rightarrow $
is a strict implication, and
$\rightarrow $
is a strict implication, and
![]() $[A]B$
is read as “in an act of imagination with content expressed by A, the agent imagines content expressed by B.” Negation and conjunction are Boolean. We define
$[A]B$
is read as “in an act of imagination with content expressed by A, the agent imagines content expressed by B.” Negation and conjunction are Boolean. We define
![]() $\vee $
(disjunction),
$\vee $
(disjunction),
![]() $\supset $
(material implication), and
$\supset $
(material implication), and
![]() $\equiv $
(material equivalence) as usual, and we sometimes omit outermost brackets. If we add
$\equiv $
(material equivalence) as usual, and we sometimes omit outermost brackets. If we add
![]() $\top $
to stand for arbitrary tautologies, we can also define a
$\top $
to stand for arbitrary tautologies, we can also define a
![]() $\square $
modality as
$\square $
modality as
![]() $\square A:=\top \rightarrow A$
. We will also call this extended language L.
$\square A:=\top \rightarrow A$
. We will also call this extended language L.
Definition 3.2 (Conditional Frame)
A conditional frame is a structure
![]() $\mathcal {F} = \langle W, \lbrace R_A\mid A\in Form(L)\rbrace \rangle $
, where W is a non-empty set of possible worlds and each
$\mathcal {F} = \langle W, \lbrace R_A\mid A\in Form(L)\rbrace \rangle $
, where W is a non-empty set of possible worlds and each
![]() $R_A$
is an accessibility relation on W indexed by a formula of the language.
$R_A$
is an accessibility relation on W indexed by a formula of the language.
Definition 3.3 (Conditional Model)
A conditional model is a structure
![]() $\mathcal {M} = \langle W, \lbrace R_A\mid A\in Form(L)\rbrace , v\rangle $
, where
$\mathcal {M} = \langle W, \lbrace R_A\mid A\in Form(L)\rbrace , v\rangle $
, where
![]() $\mathcal {F}=\langle W, \lbrace R_A\mid A\in Form(L)\rbrace \rangle $
is a conditional frame and
$\mathcal {F}=\langle W, \lbrace R_A\mid A\in Form(L)\rbrace \rangle $
is a conditional frame and
![]() $v: Var \longrightarrow \mathcal {P} (W)$
is a valuation, where
$v: Var \longrightarrow \mathcal {P} (W)$
is a valuation, where
![]() $\mathcal {P}$
is the powerset operation.
$\mathcal {P}$
is the powerset operation.
Definition 3.4 (Content frame)
A content frame is a structure
![]() $\mathcal {F}_C=\langle \textsf {C}, \oplus \rangle $
such that
$\mathcal {F}_C=\langle \textsf {C}, \oplus \rangle $
such that
![]() $\textsf {C}$
is a non-empty set of contents, and
$\textsf {C}$
is a non-empty set of contents, and
![]() $\oplus $
is an operation, called “content-fusion” (or “fusion”), such that
$\oplus $
is an operation, called “content-fusion” (or “fusion”), such that
-
Idempotency
 $x\oplus x = x$
$x\oplus x = x$
-
Commutativity
 $x\oplus y=y\oplus x$
$x\oplus y=y\oplus x$
-
Associativity
 $x\oplus (y \oplus z)=(x\oplus y)\oplus z$
$x\oplus (y \oplus z)=(x\oplus y)\oplus z$
We require that fusion is unrestricted, i.e.,
![]() $\forall y,x\exists z(z=y\oplus x)$
. A partial order
$\forall y,x\exists z(z=y\oplus x)$
. A partial order
![]() $\sqsubseteq $
on
$\sqsubseteq $
on
![]() $\textsf {C}$
is defined as usual:
$\textsf {C}$
is defined as usual:
![]() $x\sqsubseteq y$
iff
$x\sqsubseteq y$
iff
![]() $x\oplus y=y$
. We write
$x\oplus y=y$
. We write
![]() $x\sqsubset y$
iff
$x\sqsubset y$
iff
![]() $x\sqsubseteq y$
and not
$x\sqsubseteq y$
and not
![]() $y\sqsubseteq x$
. The set of atoms of
$y\sqsubseteq x$
. The set of atoms of
![]() $\textsf {C}$
is defined by
$\textsf {C}$
is defined by
![]() $Atom(\textsf {C}):=\lbrace x\in \textsf {C}\mid \neg \exists y(y\sqsubset x)\rbrace $
. We assume that this is always non-empty.
$Atom(\textsf {C}):=\lbrace x\in \textsf {C}\mid \neg \exists y(y\sqsubset x)\rbrace $
. We assume that this is always non-empty.
We turn these into content models for our formal language by adding a content assignment function.
Definition 3.5 (Content model)
A content model is a structure
![]() $\mathcal {C}=\langle \textsf {C}, \oplus , c\rangle $
such that
$\mathcal {C}=\langle \textsf {C}, \oplus , c\rangle $
such that
![]() $\langle \textsf {C}, \oplus \rangle $
is a content frame and c is a function from atomic formulas to elements of
$\langle \textsf {C}, \oplus \rangle $
is a content frame and c is a function from atomic formulas to elements of
![]() $\textsf {C}$
. The content
$\textsf {C}$
. The content
![]() $c(A)$
of an arbitrary formula A is defined as follows:
$c(A)$
of an arbitrary formula A is defined as follows:
 $c(A)=\oplus _{p_i\in Var(A)} c(p_i)$
.
$c(A)=\oplus _{p_i\in Var(A)} c(p_i)$
.
So, none of the operators adds to the content of a formula. We say that the logical vocabulary is content-transparent, or, somewhat sloppily, that content is transparent.
Giordani [Reference Giordani31] defines content models more generally in that they are always content models with respect to a possible world. Imagination models then contain a function assigning content models to worlds. This allows to vary contents across worlds. In his paper, however, he considers only standard models, which are models in which the same content model is assigned to each world, i.e., contents don’t vary across worlds. In this paper, we do the same and consider only standard models. Thus, contents are assumed not to vary across worlds.
Definition 3.6 (Berto Imagination Model)
A Berto imagination model is a structure
![]() $\mathfrak {M}=\langle W, \lbrace R_A\mid A\in Form(L)\rbrace ,v, \textsf {C}, \oplus , c\rangle $
, where
$\mathfrak {M}=\langle W, \lbrace R_A\mid A\in Form(L)\rbrace ,v, \textsf {C}, \oplus , c\rangle $
, where
![]() $\langle W, \lbrace R_A\mid A\in Form\rbrace ,v\rangle $
is a conditional model and
$\langle W, \lbrace R_A\mid A\in Form\rbrace ,v\rangle $
is a conditional model and
![]() $\langle \textsf {C}, \oplus , c\rangle $
is a content model.
$\langle \textsf {C}, \oplus , c\rangle $
is a content model.
Definition 3.7 (Truth at a world in a model)
Let
be a Berto imagination model and
![]() $w\in W$
. Then truth of a formula at world
$w\in W$
. Then truth of a formula at world
![]() $w$
in the model is defined inductively as follows:
$w$
in the model is defined inductively as follows:
 $$ \begin{align*} &\mathfrak{M}, w\vDash p \Leftrightarrow w\in v(p);\\ &\mathfrak{M}, w\vDash \neg A \Leftrightarrow \mathfrak{M}, w\nvDash A;\\ &\mathfrak{M}, w\vDash A\wedge B \Leftrightarrow \mathfrak{M}, w\vDash A\ \&\ \mathfrak{M}, w\vDash B;\\ &\mathfrak{M}, w\vDash A\rightarrow B \Leftrightarrow\forall v\in W( \mathfrak{M},v\vDash A \Rightarrow \mathfrak{M}, v\vDash B);\\ &\mathfrak{M}, w\vDash [A]B \Leftrightarrow \forall v(wR_Av \Rightarrow \mathfrak{M}, v\vDash B)\ \&\ c(B)\sqsubseteq c(A).\end{align*} $$
$$ \begin{align*} &\mathfrak{M}, w\vDash p \Leftrightarrow w\in v(p);\\ &\mathfrak{M}, w\vDash \neg A \Leftrightarrow \mathfrak{M}, w\nvDash A;\\ &\mathfrak{M}, w\vDash A\wedge B \Leftrightarrow \mathfrak{M}, w\vDash A\ \&\ \mathfrak{M}, w\vDash B;\\ &\mathfrak{M}, w\vDash A\rightarrow B \Leftrightarrow\forall v\in W( \mathfrak{M},v\vDash A \Rightarrow \mathfrak{M}, v\vDash B);\\ &\mathfrak{M}, w\vDash [A]B \Leftrightarrow \forall v(wR_Av \Rightarrow \mathfrak{M}, v\vDash B)\ \&\ c(B)\sqsubseteq c(A).\end{align*} $$
We define
![]() $\Vert A\Vert ^{\mathfrak {M}}=\lbrace w\in W\mid \mathfrak {M}, w\vDash A\rbrace $
and omit the superscript when the model is clear from context.
$\Vert A\Vert ^{\mathfrak {M}}=\lbrace w\in W\mid \mathfrak {M}, w\vDash A\rbrace $
and omit the superscript when the model is clear from context.
Let
![]() $\Sigma $
be a set of formulas and B a formula. Then B is a logical consequence of
$\Sigma $
be a set of formulas and B a formula. Then B is a logical consequence of
![]() $\Sigma $
,
$\Sigma $
,
![]() $\Sigma \models B$
, just in case in all models
$\Sigma \models B$
, just in case in all models
![]() $\mathfrak {M} = \langle W, \lbrace R_A\mid A\in Form(L)\rbrace , v, \mathcal {C}, \oplus , c \rangle $
and for all
$\mathfrak {M} = \langle W, \lbrace R_A\mid A\in Form(L)\rbrace , v, \mathcal {C}, \oplus , c \rangle $
and for all
![]() $w\in W$
, if for all
$w\in W$
, if for all
![]() $A\in \Sigma $
,
$A\in \Sigma $
,
![]() $\mathfrak {M}, w\vDash A$
, then
$\mathfrak {M}, w\vDash A$
, then
![]() $\mathfrak {M}, w\vDash B$
.
$\mathfrak {M}, w\vDash B$
.
For expositional purposes, it is sometimes easier to consider a set selection function rather than an accessibility relation. We define such a function
![]() $f: Form(L)\times W \longrightarrow \mathcal {P}(W)$
by
$f: Form(L)\times W \longrightarrow \mathcal {P}(W)$
by
![]() $f_A(w):= \lbrace w'\in W| wR_A w'\rbrace $
.
$f_A(w):= \lbrace w'\in W| wR_A w'\rbrace $
.
3.1. Berto’s validities concerning imagination
Berto considers various (in)validities concerning imaginative episodes. Some of these are only valid if certain conditions are imposed on the models. For example, to ensure that one is always successful in imagining the initial content, Berto defines admissible models to be those which satisfy the following Basic Constraint:
Definition 3.8. Let
![]() $\mathfrak {M}=\langle W, \lbrace R_A | A\in Form(L)\rbrace , v, \mathcal {C}, \oplus , c\rangle $
be a Berto-imagination model. The Basic Constraint is the following condition:
$\mathfrak {M}=\langle W, \lbrace R_A | A\in Form(L)\rbrace , v, \mathcal {C}, \oplus , c\rangle $
be a Berto-imagination model. The Basic Constraint is the following condition:
-
BC
 $\forall A\in Form(L)\forall w,v\in W(wR_Av \Rightarrow \mathfrak {M}, v\vDash A)$
$\forall A\in Form(L)\forall w,v\in W(wR_Av \Rightarrow \mathfrak {M}, v\vDash A)$
The condition BC ensures that
![]() $\vDash [A]A$
. Berto also adds the following Principle of Imaginative Equivalents:
$\vDash [A]A$
. Berto also adds the following Principle of Imaginative Equivalents:
Definition 3.9. Let
![]() $\mathfrak {M}=\langle W, \lbrace R_A | A\in Form(L)\rbrace , v, \mathcal {C}, \oplus , c\rangle $
be a Berto-imagination model. The Principle of Imaginative Equivalents is the following condition:
$\mathfrak {M}=\langle W, \lbrace R_A | A\in Form(L)\rbrace , v, \mathcal {C}, \oplus , c\rangle $
be a Berto-imagination model. The Principle of Imaginative Equivalents is the following condition:
-
PIE If
 $f_A(w) \subseteq \Vert B\Vert $
and
$f_A(w) \subseteq \Vert B\Vert $
and
 $f_B(w)\subseteq \Vert A\Vert $
, then
$f_B(w)\subseteq \Vert A\Vert $
, then
 $f_A(w)=f_B(w)$
.
$f_A(w)=f_B(w)$
.
This is an important condition because it makes conjunctions (disjunctions) in the initial input commutative and associative. That is,
![]() $[A \wedge B]C\models [B\wedge A]C$
and
$[A \wedge B]C\models [B\wedge A]C$
and
![]() $[(A \wedge B)\wedge D]C \models $
$[(A \wedge B)\wedge D]C \models $
![]() $[A\wedge (B\wedge D)]C$
(similarly for disjunction). Since the accessibility relations are indexed by formulas, without PIE, syntactically different equivalent formulas result in different accessibility relations. This is undesirable. The condition PIE allows to identify some such relations. This also semantically identifies the initial inputs
$[A\wedge (B\wedge D)]C$
(similarly for disjunction). Since the accessibility relations are indexed by formulas, without PIE, syntactically different equivalent formulas result in different accessibility relations. This is undesirable. The condition PIE allows to identify some such relations. This also semantically identifies the initial inputs
![]() $A\wedge B$
and
$A\wedge B$
and
![]() $B\wedge A$
. From a semantic perspective, if one adds PIE to the current semantics, then the resulting semantics does not distinguish between formulas at the level of grain of the syntax. Given a logic L, not distinguishing at the level of grain of L’s syntax but still having more grain of distinction than L-equivalence is desirable in discussions of hyperintensionality [Reference Saint-Germier, Giordani and Malinowski56].
$B\wedge A$
. From a semantic perspective, if one adds PIE to the current semantics, then the resulting semantics does not distinguish between formulas at the level of grain of the syntax. Given a logic L, not distinguishing at the level of grain of L’s syntax but still having more grain of distinction than L-equivalence is desirable in discussions of hyperintensionality [Reference Saint-Germier, Giordani and Malinowski56].
Call a Berto imagination model satisfying PIE, a PIE-Berto-imagination model.Footnote 14 From here on, we consider Berto’s semantics in which BC and PIE hold.
Proposition 3.10 (Validities)
The following hold:
-
Success
 $\models [A]A$
$\models [A]A$
-
Simplification
 $[A](B\wedge C) \models [A]B$
and
$[A](B\wedge C) \models [A]B$
and
 $[A](B\wedge C) \models [A]C$
$[A](B\wedge C) \models [A]C$
-
Adjunction
 $[A]B, [A]C\models [A](B\wedge C)$
$[A]B, [A]C\models [A](B\wedge C)$
-
Closure under imagined implication
 $[A](B\rightarrow C), [A]B\models [A]C$
, see [Reference Giordani31]
$[A](B\rightarrow C), [A]B\models [A]C$
, see [Reference Giordani31] -
Substitutivity
 $[A]B, [B]A, [A]C\models [B]C$
$[A]B, [B]A, [A]C\models [B]C$
-
Special Transitivity (ST)
 $[A]B, [A \wedge B]C\models [A]C$
$[A]B, [A \wedge B]C\models [A]C$
A comprehensive discussion of each of these principles is beyond the scope of this paper. But let it be said that almost each of these validities can be contested on philosophical grounds concerning imagination. We’ll shortly address each of the validities and hint at reasons for why one might not want to accept them.
Success
This principle is intended to model that agents are always successful in imagining the initial input. In light of problems concerning imaginative resistance, one might find this a problematic principle. The phenomenon of imaginative resistance can be formulated in at least four distinct ways, each of which can be considered more or less problematic [Reference Gendler, Liao, Gibson and Carroll30]. In its most prominent form, it is the phenomenon that people report to be not successful in imagining (as in mentally representing) whatever they set out to imagine or are asked to imagine. Given this phenomenon is real, one might not want to have Success around. This is especially so if one shifts the intended reading of
![]() $[A]B$
to be “given the supposition that A, the agent imagines B,” suggested in [Reference Berto11, chap. 5].
$[A]B$
to be “given the supposition that A, the agent imagines B,” suggested in [Reference Berto11, chap. 5].
Simplification
This principle seems to be an essential principle. Dropping it strips agents of the most basic understanding of conjunctions. Timothy Williamson discusses it with respect to knowing a conjunction:
Knowledge of a conjunction is already knowledge of its conjuncts. [
![]() $\ldots $
]
$\ldots $
]
![]() $\wedge $
-elimination has a rather special status. It may be brought out by a comparison with the equally canonical
$\wedge $
-elimination has a rather special status. It may be brought out by a comparison with the equally canonical
![]() $\vee $
-introduction inference to the disjunction
$\vee $
-introduction inference to the disjunction
![]() $p \vee q$
from the disjunct p or from the disjunct q. [
$p \vee q$
from the disjunct p or from the disjunct q. [
![]() $\ldots $
] A perfect logician who knows p may lack the empirical concepts to grasp (understand) the other disjunct q. Since knowing a proposition involves grasping it, and grasping a complex proposition involves grasping its constituents, such a logician is in no position to grasp
$\ldots $
] A perfect logician who knows p may lack the empirical concepts to grasp (understand) the other disjunct q. Since knowing a proposition involves grasping it, and grasping a complex proposition involves grasping its constituents, such a logician is in no position to grasp
![]() $p \vee q$
and therefore does not know
$p \vee q$
and therefore does not know
![]() $p \vee q$
. In contrast, those who know a conjunction grasp its conjuncts, for they grasp the conjunction. [
$p \vee q$
. In contrast, those who know a conjunction grasp its conjuncts, for they grasp the conjunction. [
![]() $\ldots $
] There is no obstacle here to the idea that knowing a conjunction constitutes knowing its conjuncts. [Reference Williamson69, p. 282]
$\ldots $
] There is no obstacle here to the idea that knowing a conjunction constitutes knowing its conjuncts. [Reference Williamson69, p. 282]
While one might make a case that we can imagine things beyond our grasp or understanding, it seems at least very difficult to imagine a (finite Boolean) conjunction without imagining its conjuncts. That is, to imagine a conjunction, intuitively, one needs to “imagine two things together as one whole.” This would mean that to imagine a conjunction, one doesn’t necessarily need to grasp the contents of the conjuncts (or even the conjunction as a whole). Conversely, if one could not imagine A or one could not imagine B, it seems plausible, that one also could not imagine A and B together for one lacks the imaginative capabilities for imagining one of them.
Setting a positive case for Simplification aside, we could not think of a convincing counterexample where one can be reasonably said to imagine a (finite Boolean) conjunction while not also imagining its conjuncts.
Adjunction
This principle might be objected to on grounds of bounded rationality. Adding two conjuncts into one conjunction might require additional computational resources the agent is lacking even in the involuntary unfolding of an initial input. This is even more so if we take into account that imaginative episodes extend over time and take up short-term memory. Thus we might fail in adding two conjuncts together such that one was imagined early on and the other at the end of an imaginative episode due to a bad short-term memory or just an exhaustion of our memorial capacities.Footnote
15
Moreover, it has been argued in the debate on truth in fiction, that two conjuncts being true in a fiction f does not entail that their conjunction is true in f [Reference Lewis42]. This could open one way of dealing with inconsistent fiction: both A and its negation
![]() $\neg A$
may be true in f, i.e., both A and
$\neg A$
may be true in f, i.e., both A and
![]() $\neg A$
are imagined (as the result of a given voluntary input), although
$\neg A$
are imagined (as the result of a given voluntary input), although
![]() $(A \wedge \neg A)$
is not, cf. [Reference Lewis42]. Again, if we get to what’s true in a fiction by imagining its contents, as many following [Reference Walton64] suggest, and truth in fiction is not closed under Adjunction, it seems, also imaginative episodes might not be closed under Adjunction.
$(A \wedge \neg A)$
is not, cf. [Reference Lewis42]. Again, if we get to what’s true in a fiction by imagining its contents, as many following [Reference Walton64] suggest, and truth in fiction is not closed under Adjunction, it seems, also imaginative episodes might not be closed under Adjunction.
Another reason for why one might think that imagination is not closed under Adjunction comes from comparing it to other mental states. One could think that desires and beliefs are not adjunctive. It is possible that I desire to eat a piece of chocolate and that I desire to eat a sausage with mustard. But I don’t desire eating a piece of chocolate and eating a sausage with mustard (all of this together). It’s not clear that I am irrational in this case. Also beliefs have been disputed to be adjunctive, mostly on grounds that our beliefs are often contradictory, witness the discussion above. Again, this is not sufficient to claim that an agent is irrational. So, if desires and beliefs are not adjunctive, and they form the basis of our mental architecture, as in [Reference Nichols and Stich46], this can be taken as a good reason for claiming that imagination is not adjunctive either. So, while Adjunction seems plausible at first glance, there are some reasonably strong objections to it.
Finally, consider a lottery with
![]() $2<n\in \mathbb {N}$
tickets of which you’ve bought one and your friend bought one, and in which exactly one ticket wins. Say, you imagine that a lottery ticket is drawn (p). This might unfold in the following ways: you imagine the number of your ticket
$2<n\in \mathbb {N}$
tickets of which you’ve bought one and your friend bought one, and in which exactly one ticket wins. Say, you imagine that a lottery ticket is drawn (p). This might unfold in the following ways: you imagine the number of your ticket
![]() $(q)$
, the number of your friend’s ticket
$(q)$
, the number of your friend’s ticket
![]() $(r)$
or no number on the ticket/some other number, to represent that neither of your numbers has been drawn. So,
$(r)$
or no number on the ticket/some other number, to represent that neither of your numbers has been drawn. So,
![]() $[p]q$
and
$[p]q$
and
![]() $[p]r$
might both be true but
$[p]r$
might both be true but
![]() $[p](q\wedge r)$
might fail.
$[p](q\wedge r)$
might fail.
Closure under imagined implication
This is Berto’s version of CII, which we have discussed in Section 2.1.
Substitutivity
This principle is understood as imagination being closed under imaginatively equivalent formulas. In its formulation, A and B are imaginatively equivalent because imagining one leads to imagining the other, and vice versa. In general, the principle seems plausible. There might be counterexamples to it, however. Suppose whenever I imagine that there is a four-sided figure (we represent “that there is a four-sided figure” with f), I imagine that there is a square (we represent this with s). So, using Berto’s episodic operator, we can represent this episode as
![]() $[f]s$
. Clearly, whenever I imagine that there is a square, I imagine that there is a four-sided figure. So,
$[f]s$
. Clearly, whenever I imagine that there is a square, I imagine that there is a four-sided figure. So,
![]() $[s]f$
. But, say, that whenever I imagine that there is a four-sided figure, I also imagine that there is a particular (non-square) rhomboid
$[s]f$
. But, say, that whenever I imagine that there is a four-sided figure, I also imagine that there is a particular (non-square) rhomboid
![]() $(r)$
. So,
$(r)$
. So,
![]() $[f]r$
. It doesn’t seem to follow that whenever I imagine that there is a square, I also imagine that there is a non-square rhomboid. That is, it is not the case that
$[f]r$
. It doesn’t seem to follow that whenever I imagine that there is a square, I also imagine that there is a non-square rhomboid. That is, it is not the case that
![]() $[s]r$
, contrary to what Substitutivity requires.
$[s]r$
, contrary to what Substitutivity requires.
Special Transitivity
Berto admits “[i]t may be, however, that there are intuitive counterexamples to ST, forceful enough to lead us to reject PIE” for PIE entails Substitutivity, which, in turn, entails ST. For potential counterexamples to ST we refer to (potential) counterexamples to Cautious Cut [Reference Unterhuber62], a principle of conditional logic, which also has an analogue in terms of the consequence relation in non-monotonic logic [Reference Straßer, Antonelli and Zalta59].
3.2. Invalidities
Berto also discusses some invalidities, which he considers desirable:Footnote 16
-
Indeterminacy
 $[A](B\vee C) \not \models [A]B \vee [A]C$
$[A](B\vee C) \not \models [A]B \vee [A]C$
-
No imaginative entailment
 $A\rightarrow B\not \models [A]B$
$A\rightarrow B\not \models [A]B$
-
Relevance
 $[A]B\not \models [A](B\vee C)$
$[A]B\not \models [A](B\vee C)$
-
Non-monotonicity
 $[A]B\not \models [A\wedge C]B$
$[A]B\not \models [A\wedge C]B$
-
Non-explosiveness
 $\not \models [A\wedge \neg A]B$
$\not \models [A\wedge \neg A]B$
-
No-IVF It is not the case that: if
 $\models B$
, then
$\models B$
, then
 $\models [A]B$
.Footnote
17
$\models [A]B$
.Footnote
17
Indeterminacy
The motivation behind this principle is the following. While one can imagine a striped tiger (or that there is a striped tiger), which amounts to imagining a disjunction of statements of possible numbers of stripes, one doesn’t imagine the tiger having a specific number of stripes [Reference Dennett26, p. 136]. If one holds, like Kind [Reference Kind33] and contrary to Dennett [Reference Dennett26], that imagination always involves mental imagery, one might consider Indeterminacy problematic. Of course if mental imagery makes imagination determinate, this requires the assumption that mental imagery is determinate, which is debatable itself [Reference Thomas and Zalta60].
Imaginative entailment
This principle might seem plausible if one buys into the suppositional heuristic for the semantics or/and the epistemology of conditionals. On this account, for accepting a conditional, it is necessary to imagine that B on the supposition that A. So, at least the acceptance of a conditional should then entail the corresponding imaginative episode.
Relevance
If we take seriously the idea that there must be some form of relevant connection between input and output, the truth of a (non-relevant) conditional does not entail that an agent performs an imaginative episode with the antecedent as initial input and the consequent as output. The relevance considerations are also what justifies Relevance. Disjunction-introduction introduces arbitrary content. Since imaginative episodes are constrained by a certain content, it should not be possible to simply introduce arbitrary content into one’s imaginings.
Non-Monotonicity
Imaginative episodes are sensitive to choosing new initial inputs, as is evidenced by Langland-Hassan’s notion of “cyclical top-down intentions,” which add new contents at a step in an imaginative episode [Reference Langland-Hassan, Kind and Kung40]. This affects the subsequent unfolding of the new episode and is accounted for by Non-monotonicity. Suppose in imagining that one was in a restaurant, one also imagines that the waiter is friendly. If one now imagines being in a restaurant and the waiter pointing a gun at oneself, one does not necessarily imagine that the waiter is friendly.
Non-Explosiveness
We already presented arguments for deeming initial acts of imagining a contradiction
![]() $(A \wedge \neg A)$
possible. But then there seems to be no reason to assume that in an act of imagination with content expressed by
$(A \wedge \neg A)$
possible. But then there seems to be no reason to assume that in an act of imagination with content expressed by
![]() $(A \wedge \neg A)$
, the agent imagines content expressed by an arbitrary formula B. The relevance considerations that justify Relevance also justify Non-explosiveness.
$(A \wedge \neg A)$
, the agent imagines content expressed by an arbitrary formula B. The relevance considerations that justify Relevance also justify Non-explosiveness.
Omni-Imagination
How does Berto’s semantics for imagination fare wrt IVF-CII and hyperintensionality? Since we are now dealing with a conditional imagination operator, it is not so clear how IVF-CII should be formulated. It seems plausible that “it is imagined that” in IVF-CII should be read as “given some input A, it is imagined that.”
We obtain different “episodic” versions of IVF-CII, differing with respect whether we focus on the output or the input.Footnote 18
-
eIVF if B is valid, then
 $[A]B$
is valid.
$[A]B$
is valid. -
eNIUF-out if B is unsatisfiable, then
 $[A]B$
is unsatisfiable.
$[A]B$
is unsatisfiable. -
eNIUF-in if A is unsatisfiable, then
 $[A]B$
is unsatisfiable.
$[A]B$
is unsatisfiable. -
eCVI if
 $B\supset C$
is valid, then
$B\supset C$
is valid, then
 $[A]B\supset [A]C$
is valid.
$[A]B\supset [A]C$
is valid. -
eCVE-out if
 $A\equiv B$
is valid, then
$A\equiv B$
is valid, then
 $[C]A\equiv [C]B$
is valid.
$[C]A\equiv [C]B$
is valid. -
eCVE-in if
 $A\equiv B$
is valid, then
$A\equiv B$
is valid, then
 $[A]C\equiv [B]C$
is valid.
$[A]C\equiv [B]C$
is valid. -
eCII
 $[A]B, [A](B\supset C)\models [A]C$
.
$[A]B, [A](B\supset C)\models [A]C$
.
No-eIVF
Consider eIVF and assume A is a tautology. By Success,
![]() $\models [A]A$
. The formula
$\models [A]A$
. The formula
![]() $[A]A$
is read as “in imagination act A, it is imagined that A.” It does not, however, capture the “it is imagined that” of eIVF due to its conditional formulation. The worries about the initial formulation of IVF concern the case in which we introduce an arbitrary tautology into our imagination. So, the best way to read IVF seems to be “given some imaginative input A and
$[A]A$
is read as “in imagination act A, it is imagined that A.” It does not, however, capture the “it is imagined that” of eIVF due to its conditional formulation. The worries about the initial formulation of IVF concern the case in which we introduce an arbitrary tautology into our imagination. So, the best way to read IVF seems to be “given some imaginative input A and
![]() $\models B$
, then
$\models B$
, then
![]() $\models [A]B$
.” As No-IVF shows, due to the condition on contents, this is not generally true. So eIVF fails in Berto’s semantics, which is desirable.
$\models [A]B$
.” As No-IVF shows, due to the condition on contents, this is not generally true. So eIVF fails in Berto’s semantics, which is desirable.
eNIUF
For similar reasons as before, the episodic analogue of NIUF should be read as “given some input A, if B is unsatisfiable, so is
![]() $[A]B$
.” But
$[A]B$
.” But
![]() $[A]B$
might be satisfiable. Consider the case when A is also unsatisfiable. The condition BC guarantees that there are no
$[A]B$
might be satisfiable. Consider the case when A is also unsatisfiable. The condition BC guarantees that there are no
![]() $R_A$
-accessible worlds if A is unsatisfiable. Then the first conjunct of the truth-condition for
$R_A$
-accessible worlds if A is unsatisfiable. Then the first conjunct of the truth-condition for
![]() $[A]B$
is vacuously satisfied. Consider as an example
$[A]B$
is vacuously satisfied. Consider as an example
![]() $[p\wedge \neg p](p\wedge \neg p)$
and
$[p\wedge \neg p](p\wedge \neg p)$
and
![]() $[p\wedge \neg p]\neg (p\wedge \neg p)$
, which are both valid (and hence satisfiable). So, eNIUF doesn’t hold in general.Footnote
19
$[p\wedge \neg p]\neg (p\wedge \neg p)$
, which are both valid (and hence satisfiable). So, eNIUF doesn’t hold in general.Footnote
19
eCVI
Considering the original formulation CVI, eCVI should be read as “given some input A, if
![]() $\models B\supset C$
, then
$\models B\supset C$
, then
![]() $\models [A]B\supset [A]C$
.” Since it might be that
$\models [A]B\supset [A]C$
.” Since it might be that
![]() $c(B)\sqsubseteq c(A)$
and
$c(B)\sqsubseteq c(A)$
and
![]() $c(C)\not \sqsubseteq c(A)$
, this doesn’t hold in general.
$c(C)\not \sqsubseteq c(A)$
, this doesn’t hold in general.
Hyperintensionality and eCVE
As we are considering an episodic imagination operator, logically equivalent formulas can be substituted for each other in the input or in the output, motivating the two episodic analogues of CVE. Both versions fail in Berto’s semantics due to the content condition of the truth-condition. For eCVE-out, suppose
![]() $[C]A$
and
$[C]A$
and
![]() $\models A\equiv B$
, it doesn’t follow that
$\models A\equiv B$
, it doesn’t follow that
![]() $[C]B$
for we can consider a model in which
$[C]B$
for we can consider a model in which
![]() $c(B)\not \sqsubseteq c(C)$
. Consider the following counterexample: let
$c(B)\not \sqsubseteq c(C)$
. Consider the following counterexample: let
![]() $W=\lbrace w, w_1\rbrace $
,
$W=\lbrace w, w_1\rbrace $
,
![]() $c(p)\sqsubseteq c(r)$
,
$c(p)\sqsubseteq c(r)$
,
![]() $c(q)\not \sqsubseteq c(r)$
,
$c(q)\not \sqsubseteq c(r)$
,
![]() $R_A=\emptyset $
for all A. It follows that
$R_A=\emptyset $
for all A. It follows that
![]() $w\vDash [r]p$
but
$w\vDash [r]p$
but
![]() $w\not \vDash [r](p\wedge (p\vee q))$
because
$w\not \vDash [r](p\wedge (p\vee q))$
because
![]() $c(q)\sqsubseteq c(p\wedge (p\vee q)) = c(p)\oplus c(q) \not \sqsubseteq c(r)$
.
$c(q)\sqsubseteq c(p\wedge (p\vee q)) = c(p)\oplus c(q) \not \sqsubseteq c(r)$
.
For eCVE-in, if we suppose
![]() $[A]C$
and
$[A]C$
and
![]() $\models A\equiv B$
, it might be that
$\models A\equiv B$
, it might be that
![]() $c(C)\not \sqsubseteq c(B)$
. Consider the following counterexample: let
$c(C)\not \sqsubseteq c(B)$
. Consider the following counterexample: let
![]() $W=\lbrace w, w_1\rbrace $
,
$W=\lbrace w, w_1\rbrace $
,
![]() $c(r)\sqsubseteq c(p)$
,
$c(r)\sqsubseteq c(p)$
,
![]() $c(r)\not \sqsubseteq c(q)$
,
$c(r)\not \sqsubseteq c(q)$
,
![]() $R_A=\emptyset $
for all A. It follows that
$R_A=\emptyset $
for all A. It follows that
![]() $w\vDash [p\vee \neg p]r$
but
$w\vDash [p\vee \neg p]r$
but
![]() $w\not \vDash [q\vee \neg q]r$
because
$w\not \vDash [q\vee \neg q]r$
because
![]() $c(q \vee \neg q)=c(q)$
and
$c(q \vee \neg q)=c(q)$
and
![]() $c(r)\not \sqsubseteq c(q)$
.
$c(r)\not \sqsubseteq c(q)$
.
There are problems with PIE and substitution in the initial input, however, as pointed out by Saint-Germier [Reference Saint-Germier, Giordani and Malinowski56]. In fact, PIE and BC entail that
![]() $[A]B\models [A']B$
if
$[A]B\models [A']B$
if
![]() $\models A\equiv A'$
and
$\models A\equiv A'$
and
![]() $c(A)\sqsubseteq c(A')$
. So, a weakened version of eCVE does still hold in Berto’s semantics.
$c(A)\sqsubseteq c(A')$
. So, a weakened version of eCVE does still hold in Berto’s semantics.
Proposition 3.11 (Weak eCVE)
If
![]() $\models A\equiv A'$
and
$\models A\equiv A'$
and
![]() $c(A)\sqsubseteq c(A')$
, then
$c(A)\sqsubseteq c(A')$
, then
![]() $[A]B\models [A']B$
.
$[A]B\models [A']B$
.
Berto cannot simply drop PIE because, as mentioned, then
![]() $R_{A\wedge B}$
and
$R_{A\wedge B}$
and
![]() $R_{B\wedge A}$
might differ, which leads to implausible consequences. In our semantics, we will be able to drop an analogue of PIE and maintain that
$R_{B\wedge A}$
might differ, which leads to implausible consequences. In our semantics, we will be able to drop an analogue of PIE and maintain that
![]() $[A\wedge B]C\models [B\wedge A]C$
because we consider a relation indexed by sets of evaluation indices. Saint-Germier [Reference Saint-Germier, Giordani and Malinowski56] chooses to use truthmaker semantics to overcome the problems caused by PIE. For this paper, we accept that the agents we model are idealised in that logically equivalent formulas may be substituted in the initial input. These initial imaginings, however, will not unfold to all logically equivalent formulas. If we drop the content inclusion restrictions, Berto’s as well as our semantics satisfies closure under valid equivalence also for the involuntary output of imagination episodes. Without the content restriction, we only need to consider the first conjunct of the truth-condition for the imagination operator. If
$[A\wedge B]C\models [B\wedge A]C$
because we consider a relation indexed by sets of evaluation indices. Saint-Germier [Reference Saint-Germier, Giordani and Malinowski56] chooses to use truthmaker semantics to overcome the problems caused by PIE. For this paper, we accept that the agents we model are idealised in that logically equivalent formulas may be substituted in the initial input. These initial imaginings, however, will not unfold to all logically equivalent formulas. If we drop the content inclusion restrictions, Berto’s as well as our semantics satisfies closure under valid equivalence also for the involuntary output of imagination episodes. Without the content restriction, we only need to consider the first conjunct of the truth-condition for the imagination operator. If
![]() $\models B\equiv B'$
, then a world is a B-world iff it is a
$\models B\equiv B'$
, then a world is a B-world iff it is a
![]() $B'$
-world. So all
$B'$
-world. So all
![]() $R_A$
-accessible worlds are B-worlds iff they are
$R_A$
-accessible worlds are B-worlds iff they are
![]() $B'$
-worlds.
$B'$
-worlds.
eCII
We have pointed out before that CII might be objected to. Berto’s semantics validates eCII,
![]() $[A]B$
,
$[A]B$
,
![]() $[A](B\rightarrow C) \models [A]C$
, which is the episodic analogue of CII.Footnote
20
$[A](B\rightarrow C) \models [A]C$
, which is the episodic analogue of CII.Footnote
20
3.3. Taking stock
So, summing up the discussion of the above (in)validities, one might have reasons to reject or accept some of them, which calls for a semantics flexible enough for having them around (or not). Our semantics will be highly flexible in this respect due to the frame correspondence results. It will, however, inherit an analogue of the issue raised by Saint-Germier, and so it won’t invalidate one version of CVE. Nevertheless, we are obtaining a lot more flexibility than Berto’s initial account.
Observe that the following holds in Berto’s semantics, where
![]() $\supset $
is material implication:
$\supset $
is material implication:
Remark 3.12. Let
![]() $A_1, \ldots , A_n$
, B be formulas. Then
$A_1, \ldots , A_n$
, B be formulas. Then
![]() $A_1,\ldots ,A_n\models B$
iff
$A_1,\ldots ,A_n\models B$
iff
![]() $\models (A_1 \wedge \cdots \wedge A_n)\supset B$
.
$\models (A_1 \wedge \cdots \wedge A_n)\supset B$
.
The formulas for which we prove correspondence results will be axiomatic analogues of Berto’s validity statements, or, more accurately, the respective logical truths derived from them following the previous observation. They are analogues in the sense that we replace Berto’s conditional imagination operator with our conditional imagination operator, which is defined in terms of Berto’s conditional imagination operator, Wansing and Olkhovikov’s voluntary imagination operator, and a neighborhood modality. We now introduce our semantics, then discuss IVF-CVE, and then prove various frame correspondences. After that we discuss our results and shortly compare it with recent work by [Reference Canavotto, Giordani and Berto15].
4. Semantics for imaginative episodes with voluntary input
We now go on to combine the voluntary imagination operator from [Reference Olkhovikov and Wansing48, Reference Olkhovikov and Wansing49, Reference Wansing67] with Berto’s episodic imagination operator. First, we recapitulate the semantics of stit-imagination logic to then expand on it.
Stit-imagination logic builds on what is perhaps the most prevailing logic for modelling reasoning about the concrete agency of decision making independent agents in branching time, namely the theory of seeing-to-it-that, stit-theory, due to Nuel Belnap, Michael Perloff, and Ming Xu [Reference Belnap, Perloff and Xu6]. They introduced two modal operators (in infix notation) for expressing agentive statements, the achievement stit (astit) operator and the deliberative stit (dstit) operator. Whereas in the semantics of the astit operator the moment of choice of an agent precedes the moment of evaluation of formulas expressing that the agent sees to it that something is the case, the semantics of the dstit operator is simpler and does not draw a distinction between the moment of choice and the moment of semantic evaluation. It has now become quite common to work with the dstit operator instead of the achievement stit operator. The semantics of the dstit operator models genuine agency of agents insofar as it requires that if an agent deliberately sees to it that A, then A is not settled true, i.e., A is not true with respect to every temporal development from the moment of evaluation to future moments. An even simpler seeing-to-it that operator is the cstit (Chellas-stit) operator. The cstit operator is an
![]() $S5$
necessity-type operator, and if it is assumed as a primitive connective, it can be used to define the dstit operator in combination with the “settled true” modality. Agency as captured by the cstit operator can also be understood as agency in the sense of “seeing-to-it-that” but it is often referred to as
$S5$
necessity-type operator, and if it is assumed as a primitive connective, it can be used to define the dstit operator in combination with the “settled true” modality. Agency as captured by the cstit operator can also be understood as agency in the sense of “seeing-to-it-that” but it is often referred to as
![]() $cstit$
-realization.
$cstit$
-realization.
The language of stit-imagination logic,
![]() , has a countable set of atomic formulas
, has a countable set of atomic formulas
![]() $Var=\lbrace p_i, q_i, r_i,\ldots \rbrace $
. We again use p, q, r as schematic atomic formulas. The vocabulary comprises operators
$Var=\lbrace p_i, q_i, r_i,\ldots \rbrace $
. We again use p, q, r as schematic atomic formulas. The vocabulary comprises operators
![]() $\neg , \wedge , S, [c]_a, \square _a$
, for each agent a from a set of agents
$\neg , \wedge , S, [c]_a, \square _a$
, for each agent a from a set of agents
![]() $Ag$
. The set of formulas is given by the following Backus–Naur grammar:
$Ag$
. The set of formulas is given by the following Backus–Naur grammar:
where
![]() $p \in Var$
. We define
$p \in Var$
. We define
![]() $\vee $
(disjunction), and
$\vee $
(disjunction), and
![]() $\supset $
(material implication) as usual and we sometimes omit outermost brackets. The intended readings of the formulas are as follows:
$\supset $
(material implication) as usual and we sometimes omit outermost brackets. The intended readings of the formulas are as follows:
![]() $SA$
is read as “A is settled true,”
$SA$
is read as “A is settled true,”
![]() $[c]_a A$
is read as “agent
$[c]_a A$
is read as “agent
![]() $a\ cstit$
-realizes A,”
$a\ cstit$
-realizes A,”
![]() $\square _a A$
is read as “A is in a’s mental image.”
$\square _a A$
is read as “A is in a’s mental image.”
The language of stit-imagination episode logic,
![]() $\mathcal {L}$
, is
$\mathcal {L}$
, is
extended by formulas of the following form:
where
.Footnote 21 The intended reading of
is “if A, then B,” where the content of B is included in the content of A. We define the deliberate-choice imagination operator as follows
The intended reading of this is “agent a voluntarily imagines that A,” which we treat as equivalent with “a deliberately chooses to imagine that A.” We define the episodic imagination modality by
which is read as “if the agent voluntarily imagines that A, then they have B in their mental image” or “if the agent voluntarily imagines that A, then they involuntarily imagine that B.” For simplicity, we keep calling the extended language
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Before delving into the semantics, let us say a few words about why we work in a multi-agent setting. This has to do with embedded imaginings. First, imagination is often considered to be necessary when engaging with narratives, especially narrative fiction [Reference Currie24, Reference Stock58, Reference Walton64]. There are narrative fictions such as Michael Ende’s The Neverending Story, in which we are required to imagine that some character imagines something.Footnote 22
Moreover, in planning and strategic thinking, we are often imagining what someone else is imagining. Adam Morton discusses imagining imagining in the context of planning and argues that agents are usually fairly accurate in imagining another’s imaginings. In Morton’s example there are two people a and b at opposite sides of a crowded hall filled with people, tables, pillars, etc. and they aim to meet somewhere in the middle. He suggests that
from the very beginning each will take account of the obstacles facing the other in order to imagine the route the other will take. In fact, they will imagine each other’s imagining of themselves, in order to anticipate choices that each will make as a result of imagining the possibilities open to the other. So in planning a coordinated action, each person is imagining the other person’s imagining their planning. [Reference Morton and Nichols44, pp. 68–69]
Since we have distinguished philosophically between imaginative states and imaginative episodes, and this distinction is captured in the language by defining two imagination operators, there are various ways in which we can understand that a imagines that b imagines a’s planning. Following Morton, we can understand a’s planning an action as an imaginative episode, in which doing the action is voluntarily imagined and then its consequences unfold.Footnote 23
The fact that imagining an imagining is usually accurate, Morton claims, is due to the agent’s limited options to “graft one information structure on to another” [Reference Morton and Nichols44, p. 69]. In imagining that b is imagining, a imagines b’s perspective and then simulates how b’s imagination would go. So, according to Morton, it seems, embedded imagination is always episodic in that a initially imagines the initial input they think b would imagine, and then a’s imagining unfolds in such a way that a ends up with what they think b’s imagining would unfold to. Importantly, a does not deliberately imagine b’s whole imaginative episode but only deliberately imagines what they think b is deliberately imagining as initial input. This then unfolds to what b’s imagining unfolds to. This is expressed by
![]() , which is equivalent to
, which is equivalent to
![]() $I_bI_a p_1[a]\!\!\!\rightarrow \! \square _b\square _a p_2$
. So, the syntactic restriction doesn’t prevent us from expressing embedded imaginings in a philosophically natural way.
$I_bI_a p_1[a]\!\!\!\rightarrow \! \square _b\square _a p_2$
. So, the syntactic restriction doesn’t prevent us from expressing embedded imaginings in a philosophically natural way.
Although embedded imaginings are interesting, we are not going to tackle them further in this paper. Nevertheless, it is useful to have a language and semantics expressive enough to investigate certain kinds of embedded imaginings. To the best of our knowledge, the issue of embedded imaginings hasn’t been addressed in the logical literature. In particular, it hasn’t been noted that there are different kinds of embedded imaginings as soon as we distinguish between voluntary imaginings, which correspond to imaginative states, and imaginative episodes.
Let us now turn to the semantics. We start by defining the stit-imagination frames, necessary to interpret the agentive imagination modality.
Definition 4.13. (Stit-imagination frame)
A stit-imagination frame is a structure
where the tuple
![]() $\langle Tree, \leq , Ag, Choice \rangle $
is a branching-time plus agent choice frame from stit-theory, which means that:
$\langle Tree, \leq , Ag, Choice \rangle $
is a branching-time plus agent choice frame from stit-theory, which means that:
-
1.
 $Tree$
is a non-empty set of moments, and
$Tree$
is a non-empty set of moments, and
 $\leq $
is a partial order on
$\leq $
is a partial order on
 $Tree$
such that
$Tree$
such that-
No Backwards Branching
 $\forall m_1,m_2\exists m(m \leq m_1 \wedge m \leq m_2).$
$\forall m_1,m_2\exists m(m \leq m_1 \wedge m \leq m_2).$
-
Historical Connectedness
 $\forall m_1,m_2,m((m_1 \leq m \wedge m_2 \leq m) \Rightarrow (m_1 \leq m_2 \vee m_2 \leq m_1)).$
$\forall m_1,m_2,m((m_1 \leq m \wedge m_2 \leq m) \Rightarrow (m_1 \leq m_2 \vee m_2 \leq m_1)).$
 $History$
of all histories of
$History$
of all histories of
 $\mathcal {F}$
is the set of all maximal
$\mathcal {F}$
is the set of all maximal
 $\leq $
-chains in
$\leq $
-chains in
 $Tree$
. If
$Tree$
. If
 $m \in h$
, then history h is said to pass through moment m, and
$m \in h$
, then history h is said to pass through moment m, and
 $H_m :=\{h \mid h \in m\}$
.
$H_m :=\{h \mid h \in m\}$
.
-
-
2.
 $Ag$
is a finite and non-empty set of agents (the same for all frames).
$Ag$
is a finite and non-empty set of agents (the same for all frames). -
3.
 $Choice:Tree \times Ag\longrightarrow 2^{History}$
such that for an arbitrary
$Choice:Tree \times Ag\longrightarrow 2^{History}$
such that for an arbitrary
 $(m, a) \in Tree \times Ag$
,
$(m, a) \in Tree \times Ag$
,
 $Choice(m,a)$
(usually denoted
$Choice(m,a)$
(usually denoted
 $Choice^m_a$
) is a partition of
$Choice^m_a$
) is a partition of
 $H_m$
. Intuitively,
$H_m$
. Intuitively,
 $Choice^m_a$
represents agent a’s choice cells at moment m. If
$Choice^m_a$
represents agent a’s choice cells at moment m. If
 $h \in H_m$
, then
$h \in H_m$
, then
 $Choice^m_a(h)$
denotes the element of
$Choice^m_a(h)$
denotes the element of
 $Choice^m_a$
to which h belongs. The function
$Choice^m_a$
to which h belongs. The function
 $Choice$
is assumed to satisfy the following two restrictions:
$Choice$
is assumed to satisfy the following two restrictions: -
No choice between undivided histories for arbitrary
 $m\in Tree$
,
$m\in Tree$
,
 $a \in Ag$
,
$a \in Ag$
,
 $e\in Choice^m_a$
, and
$e\in Choice^m_a$
, and
 $h,h' \in H_m$
:
$h,h' \in H_m$
:
 $(h \in e \wedge \exists m'(m < m' \wedge m' \in h \cap h')) \Rightarrow h' \in e.$
$(h \in e \wedge \exists m'(m < m' \wedge m' \in h \cap h')) \Rightarrow h' \in e.$
-
Independence of agents If f is a function defined on
 $Ag$
such that
$Ag$
such that
 $\forall a \in Ag (f(a) \in Choice_a^m)$
, then
$\forall a \in Ag (f(a) \in Choice_a^m)$
, then
 $\bigcap _{a \in Ag}f(a) \neq \varnothing $
.
$\bigcap _{a \in Ag}f(a) \neq \varnothing $
.
-
The set
![]() $MH({Tree}) = \{ (m, h) \mid m \in Tree, h \in H_m \}$
of all moment/history-pairs in
$MH({Tree}) = \{ (m, h) \mid m \in Tree, h \in H_m \}$
of all moment/history-pairs in
![]() $\mathcal {F}$
serves as the set of points where formulas are evaluated, so that
$\mathcal {F}$
serves as the set of points where formulas are evaluated, so that
![]() $\mathcal {P} (MH({Tree}))$
, the powerset of
$\mathcal {P} (MH({Tree}))$
, the powerset of
![]() $MH({Tree})$
, contains among its elements the truth-sets of formulas of the language.Footnote
24
For every
$MH({Tree})$
, contains among its elements the truth-sets of formulas of the language.Footnote
24
For every
![]() $a \in Ag$
,
$a \in Ag$
,
![]() $N_a$
:
$N_a$
:
![]() $MH({Tree}) \longrightarrow \mathcal {P} (\mathcal {P} (MH({Tree})))$
, i.e.,
$MH({Tree}) \longrightarrow \mathcal {P} (\mathcal {P} (MH({Tree})))$
, i.e.,
![]() $N_a$
is a function that maps moment/history-pairs to families of sets of moment/history-pairs. Intuitively,
$N_a$
is a function that maps moment/history-pairs to families of sets of moment/history-pairs. Intuitively,
![]() $N_a$
assigns to every moment history pair
$N_a$
assigns to every moment history pair
![]() $(m,h)$
the set of propositions that are part of agent a’s mental image at
$(m,h)$
the set of propositions that are part of agent a’s mental image at
![]() $(m,h)$
.
$(m,h)$
.
Let
![]() $\mathcal {F} = \langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \} \rangle $
be a stit imagination frame. Then a pair
$\mathcal {F} = \langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \} \rangle $
be a stit imagination frame. Then a pair
![]() $\mathcal {M} = \langle \mathcal {F}, v\rangle $
is a stit-imagination model based on
$\mathcal {M} = \langle \mathcal {F}, v\rangle $
is a stit-imagination model based on
![]() $\mathcal F$
iff
$\mathcal F$
iff
![]() $v$
is an evaluation function for propositional variables, i.e.,
$v$
is an evaluation function for propositional variables, i.e.,
![]() $v: Var \longrightarrow \mathcal {P} (MH({Tree}))$
.
$v: Var \longrightarrow \mathcal {P} (MH({Tree}))$
.
We next introduce some further ingredients to our semantics that allow us to define a non-agentive episodic imagination operator similar to Berto’s. The first ingredient is a ternary relation
![]() $R_{\epsilon }$
as used to interpret conditionals in conditional logic. The idea behind the ternary relation is that it connects two evaluation indices, in our case moment/history pairs, via some third entity
$R_{\epsilon }$
as used to interpret conditionals in conditional logic. The idea behind the ternary relation is that it connects two evaluation indices, in our case moment/history pairs, via some third entity
![]() $\epsilon $
. In conditional logic, the relation features in the truth-condition for the conditional. In the truth-condition,
$\epsilon $
. In conditional logic, the relation features in the truth-condition for the conditional. In the truth-condition,
![]() $\epsilon $
is instantiated with respect to the antecedent of the conditional. In Berto’s semantics,
$\epsilon $
is instantiated with respect to the antecedent of the conditional. In Berto’s semantics,
![]() $\epsilon $
is a formula. In the truth-condition for formulas of the form
$\epsilon $
is a formula. In the truth-condition for formulas of the form
![]() $[A]B$
,
$[A]B$
,
![]() $\epsilon $
is the antecedent formula A–an element from the syntax. In our setting,
$\epsilon $
is the antecedent formula A–an element from the syntax. In our setting,
![]() $\epsilon $
is a set of evaluation indices. Such a set is a proper semantic entity, rather than an element from the syntax. As a particular case, in the truth condition for
$\epsilon $
is a set of evaluation indices. Such a set is a proper semantic entity, rather than an element from the syntax. As a particular case, in the truth condition for
![]() we will get that the accessibility relation is indexed by the truth-set of A. This captures that imagination is a mental process that involves semantic representations. Since we are using an accessibility relation annotated by a set of indices rather than a formula, we need to ensure that for each formula A that can feature as antecedent of
we will get that the accessibility relation is indexed by the truth-set of A. This captures that imagination is a mental process that involves semantic representations. Since we are using an accessibility relation annotated by a set of indices rather than a formula, we need to ensure that for each formula A that can feature as antecedent of
![]() we have its truth-set around, so the accessibility relation can be annotated by this truth-set. To ensure this, we employ general frames the role of which is exactly to ensure that all/the right truth-sets are “available.” General frames are a standard tool in modal logic [Reference Blackburn, de Rijke and Venema13] and have been applied in the context of conditional logics [Reference Chellas20, Reference Chellas21, Reference Segerberg57, Reference Unterhuber62, Reference Unterhuber and Schurz63, Reference Wansing and Unterhuber68]. General frames in our setting contain an element P, which is a set of subsets of
we have its truth-set around, so the accessibility relation can be annotated by this truth-set. To ensure this, we employ general frames the role of which is exactly to ensure that all/the right truth-sets are “available.” General frames are a standard tool in modal logic [Reference Blackburn, de Rijke and Venema13] and have been applied in the context of conditional logics [Reference Chellas20, Reference Chellas21, Reference Segerberg57, Reference Unterhuber62, Reference Unterhuber and Schurz63, Reference Wansing and Unterhuber68]. General frames in our setting contain an element P, which is a set of subsets of
![]() $MH(Tree)$
, the role of which is to ensure that for each formula that can feature as antecedent of formulas of the form
$MH(Tree)$
, the role of which is to ensure that for each formula that can feature as antecedent of formulas of the form
![]() its truth-set is in P. As per our syntactic restriction, formulas of the form
its truth-set is in P. As per our syntactic restriction, formulas of the form
![]() cannot have formulas of the same form in the antecedent. Hence, it is never necessary to consider truth-sets of formulas of this form as annotations of R. Consequently, P does not have to ensure that the truth set of formulas of the form
cannot have formulas of the same form in the antecedent. Hence, it is never necessary to consider truth-sets of formulas of this form as annotations of R. Consequently, P does not have to ensure that the truth set of formulas of the form
![]() is around.
is around.
Since we intend
![]() to be a content-sensitive conditional operator, we also enrich our frames by a set of contents
to be a content-sensitive conditional operator, we also enrich our frames by a set of contents
![]() $\textsf {C}$
and an operation
$\textsf {C}$
and an operation
![]() $\oplus $
, such that
$\oplus $
, such that
![]() $\langle \textsf {C}, \oplus \rangle $
is a content frame. This way, we arrive at the following definition of the frames relevant for our purposes:
$\langle \textsf {C}, \oplus \rangle $
is a content frame. This way, we arrive at the following definition of the frames relevant for our purposes:
Definition 4.14 (Rich general stit-imagination episode frame/Frame)
A structure
![]() $\mathcal {F} = \langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \}, R, P, \textsf {C}, \oplus \rangle $
is a rich general stit-imagination episode frame (frame) iff
$\mathcal {F} = \langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \}, R, P, \textsf {C}, \oplus \rangle $
is a rich general stit-imagination episode frame (frame) iff
-
•
 $\langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag\} \rangle $
is a stit-imagination frame,
$\langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag\} \rangle $
is a stit-imagination frame, -
•
 $\langle \textsf {C}, \oplus \rangle $
is a content frame,
$\langle \textsf {C}, \oplus \rangle $
is a content frame, -
•
 $R \subseteq MH(Tree)\times \mathcal {P}(MH(Tree))\times MH(Tree)$
is a ternary relation relating two moment/history pairs and a set of moment/history pairs, notation:
$R \subseteq MH(Tree)\times \mathcal {P}(MH(Tree))\times MH(Tree)$
is a ternary relation relating two moment/history pairs and a set of moment/history pairs, notation:
 $(m,h)R_X(m',h')$
,
$(m,h)R_X(m',h')$
, -
•
 $P \subseteq \mathcal {P} (MH(Tree))$
satisfies the following conditions:
$P \subseteq \mathcal {P} (MH(Tree))$
satisfies the following conditions:-
1.
 $\varnothing \in P$
,
$\varnothing \in P$
, -
2. if
 $X \in P$
, then
$X \in P$
, then
 $MH(Tree) \setminus X \in P$
,
$MH(Tree) \setminus X \in P$
, -
3. if
 $X, Y \in P$
, then
$X, Y \in P$
, then
 $X \cap Y \in P$
,
$X \cap Y \in P$
, -
4. if
 $X \in P$
, then
$X \in P$
, then
 $\{(m,h) \!\in\! MH(\textit{Tree}) \mid \forall h' (h' \!\in\! H_m \!\Rightarrow\! (m,h') \!\in\! X)\} \!\in\! P$
,
$\{(m,h) \!\in\! MH(\textit{Tree}) \mid \forall h' (h' \!\in\! H_m \!\Rightarrow\! (m,h') \!\in\! X)\} \!\in\! P$
, -
5. if
 $X \!\in\! P$
and
$X \!\in\! P$
and
 $a \!\in\! Ag$
, then
$a \!\in\! Ag$
, then
 $\{(m,h) \!\in\! MH(\textit{Tree}) \mid \forall h' (h' \!\in\! Choice^m_{a} (h) \!\Rightarrow\! (m,h') \in X)\} \in P$
,
$\{(m,h) \!\in\! MH(\textit{Tree}) \mid \forall h' (h' \!\in\! Choice^m_{a} (h) \!\Rightarrow\! (m,h') \in X)\} \in P$
, -
6. if
 $X \!\in\! P$
and
$X \!\in\! P$
and
 $a \!\in\! Ag$
, then
$a \!\in\! Ag$
, then
 $\{(m,h)\!\in\! MH(Tree) \mid X \!\in\! N_a((m,h))\}\!\in\! P$
$\{(m,h)\!\in\! MH(Tree) \mid X \!\in\! N_a((m,h))\}\!\in\! P$
-
Models are defined from this by adding a valuation of the propositional variables, and adding a content-assignment for all propositional variables:
Definition 4.15 (Rich general stit-imagination episode model/Model)
A structure
is a rich general stit-imagination episode model (model) iff
is a rich general stit-imagination episode frame,
![]() $\mathcal {C}=\langle \textsf {C}, \oplus \rangle $
is a content frame,
$\mathcal {C}=\langle \textsf {C}, \oplus \rangle $
is a content frame,
![]() $v: Var\longrightarrow \mathcal {P}(MH(Tree))$
is a valuation such that
$v: Var\longrightarrow \mathcal {P}(MH(Tree))$
is a valuation such that
![]() $v(p)=\Vert p\Vert \in P$
for every
$v(p)=\Vert p\Vert \in P$
for every
![]() $p \in Var$
, and
$p \in Var$
, and
![]() $c: Var \longrightarrow \textsf {C}$
is a content assignment function. We extend this content assignment function to the whole language by requiring for each formula A,
$c: Var \longrightarrow \textsf {C}$
is a content assignment function. We extend this content assignment function to the whole language by requiring for each formula A,
 $c(A)= \oplus _{p_i\in Var(A)}c(p_i)$
.
$c(A)= \oplus _{p_i\in Var(A)}c(p_i)$
.
Since the logical operators don’t add any content, we say that the logical vocabulary is content-transparent. In the following, whenever we are considering frames (models), these are rich general stit-imagination episode frames (models). Given the notion of a model, we define truth at a moment/history pair in a model:
Definition 4.16 (Truth at a moment/history pair in a model)
Truth of a formula at a moment/history pair
![]() $(m,h)$
in a model
$(m,h)$
in a model
where
![]() $(m,h)\in MH(Tree)$
,Footnote
25
is inductively defined as follows:
$(m,h)\in MH(Tree)$
,Footnote
25
is inductively defined as follows:

The expression
![]() $\Vert A \Vert ^{\mathcal {M}}$
denotes the truth-set of A in the model
$\Vert A \Vert ^{\mathcal {M}}$
denotes the truth-set of A in the model
![]() $\mathcal {M}$
, i.e.,
$\mathcal {M}$
, i.e.,
![]() $\Vert A \Vert ^{\mathcal {M}}$
=
$\Vert A \Vert ^{\mathcal {M}}$
=
![]() $\{ (m,h) \in MH(Tree) \mid \mathcal {M}, (m,h) \vDash A \}$
and thus
$\{ (m,h) \in MH(Tree) \mid \mathcal {M}, (m,h) \vDash A \}$
and thus
![]() $\mathcal {M}, (m,h)\vDash A$
iff
$\mathcal {M}, (m,h)\vDash A$
iff
![]() $(m,h)\in \Vert A\Vert ^{\mathcal {M}}$
. We usually omit the superscript
$(m,h)\in \Vert A\Vert ^{\mathcal {M}}$
. We usually omit the superscript
![]() $\mathcal {M}$
. Truth conditions for disjunctions
$\mathcal {M}$
. Truth conditions for disjunctions
![]() $(A \vee B)$
, material implications
$(A \vee B)$
, material implications
![]() $(A \supset B)$
, and material equivalences
$(A \supset B)$
, and material equivalences
![]() $(A \equiv B)$
can be derived in the standard way.
$(A \equiv B)$
can be derived in the standard way.
Given the definition of truth at a moment/history pair in a model, we can now show that P contains the truth-set of each formula from
![]() (we emphasise the restriction to the language without formulas of the form
(we emphasise the restriction to the language without formulas of the form
![]() ).
).
Proposition 4.17. Given a rich general model
![]() $\mathcal {M} = \langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \}, R, P, \textsf {C}, \oplus , c, v \rangle $
, for every formula
$\mathcal {M} = \langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \}, R, P, \textsf {C}, \oplus , c, v \rangle $
, for every formula
![]() ,
,
![]() $\Vert A\Vert \in P$
.
$\Vert A\Vert \in P$
.
Proof. The proof is a straightforward induction on the structure of A. We show the base case, and the cases for
![]() $[c]_aA$
,
$[c]_aA$
,
![]() $\square _a A$
. Let
$\square _a A$
. Let
![]() $\mathcal {M} = \langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \}, R, P, \textsf {C}, \oplus , c, v \rangle $
be a model. By definition of
$\mathcal {M} = \langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \}, R, P, \textsf {C}, \oplus , c, v \rangle $
be a model. By definition of
![]() $\mathcal {M}$
, if A is an atomic formula, say p, then
$\mathcal {M}$
, if A is an atomic formula, say p, then
![]() $v(p)=\Vert p\Vert \in P$
. For the other cases, we use the induction hypothesis, and then apply the definition of P.
$v(p)=\Vert p\Vert \in P$
. For the other cases, we use the induction hypothesis, and then apply the definition of P.
If
![]() $A=[c]_aB$
, then, by induction hypothesis,
$A=[c]_aB$
, then, by induction hypothesis,
![]() $\Vert B\Vert \in P$
. By Condition 5 of Definition 4.14, it follows that
$\Vert B\Vert \in P$
. By Condition 5 of Definition 4.14, it follows that
 $\{(m,h) \in MH(Tree) \mid \forall h' (h' \in Choice^m_{a} (h) \Rightarrow (m,h') \in \Vert B\Vert )\} = \{(m,h)\in MH(Tree)\mid \mathcal {M}, (m,h)\vDash [c]_a B\}=\Vert [c]_aB\Vert \in P$
.
$\{(m,h) \in MH(Tree) \mid \forall h' (h' \in Choice^m_{a} (h) \Rightarrow (m,h') \in \Vert B\Vert )\} = \{(m,h)\in MH(Tree)\mid \mathcal {M}, (m,h)\vDash [c]_a B\}=\Vert [c]_aB\Vert \in P$
.
If
![]() $A=\square _a B$
, then by induction hypothesis,
$A=\square _a B$
, then by induction hypothesis,
![]() $\Vert B\Vert \in P$
. By Condition 6 of Definition 4.14,
$\Vert B\Vert \in P$
. By Condition 6 of Definition 4.14,
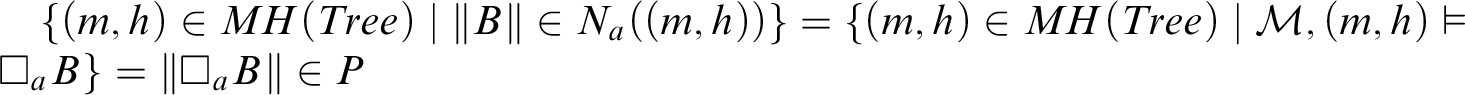 $\{(m,h)\in MH(Tree) \mid \Vert B\Vert \in N_a((m,h))\}= \{(m,h)\in MH(Tree)\mid \mathcal {M}, (m,h)\vDash \square _a B\}=\Vert \square _a B\Vert \in P$
.
$\{(m,h)\in MH(Tree) \mid \Vert B\Vert \in N_a((m,h))\}= \{(m,h)\in MH(Tree)\mid \mathcal {M}, (m,h)\vDash \square _a B\}=\Vert \square _a B\Vert \in P$
.
Since we defined
![]() $I_a A:=[c]_a\square _a A\wedge \neg S\square _a A$
and
$I_a A:=[c]_a\square _a A\wedge \neg S\square _a A$
and
![]() , it is easy to derive the following truth conditions:
, it is easy to derive the following truth conditions:
 $$ \begin{align*}\begin{array}{lcl} \mathcal{M}, (m,h) \vDash I_a A & \Leftrightarrow & \forall h' \in Choice^m_a(h) , \Vert A \Vert\in N_a((m,h'))\ \&\ \\ & & \exists h' \in H_m , \Vert A \Vert \notin N_a((m,h'));\\ \mathcal{M}, (m,h) \vDash (A [a]\!\!\!\rightarrow\! B) & \Leftrightarrow & \forall h' \in H_m , ((m,h) R_{\Vert I_a A \Vert} (m,h') \Rightarrow \\ & & \Vert B \Vert \in N_a ((m,h')))\ \&\ c(B)\sqsubseteq c(A). \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{lcl} \mathcal{M}, (m,h) \vDash I_a A & \Leftrightarrow & \forall h' \in Choice^m_a(h) , \Vert A \Vert\in N_a((m,h'))\ \&\ \\ & & \exists h' \in H_m , \Vert A \Vert \notin N_a((m,h'));\\ \mathcal{M}, (m,h) \vDash (A [a]\!\!\!\rightarrow\! B) & \Leftrightarrow & \forall h' \in H_m , ((m,h) R_{\Vert I_a A \Vert} (m,h') \Rightarrow \\ & & \Vert B \Vert \in N_a ((m,h')))\ \&\ c(B)\sqsubseteq c(A). \end{array}\end{align*} $$
A formula A is true in a model
just in case for all
![]() $(m,h)\in MH(Tree)$
,
$(m,h)\in MH(Tree)$
,
![]() $\mathcal {M}, (m,h)\vDash A$
. In that case we write
$\mathcal {M}, (m,h)\vDash A$
. In that case we write
![]() $\mathcal {M}\Vdash A$
. A formula A is valid on a frame
$\mathcal {M}\Vdash A$
. A formula A is valid on a frame
![]() $\langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \}, R, P, \textsf {C}, \oplus , c\rangle $
just in case for all models
$\langle Tree, \leq , Ag, Choice, \{ N_a\mid a \in Ag \}, R, P, \textsf {C}, \oplus , c\rangle $
just in case for all models
![]() $\mathcal {M}$
based on
$\mathcal {M}$
based on
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\mathcal {M}\Vdash A$
. In this case we write
$\mathcal {M}\Vdash A$
. In this case we write
![]() $\mathcal {F}\Vdash A$
. A formula is valid on a class of frames C just in case for all
$\mathcal {F}\Vdash A$
. A formula is valid on a class of frames C just in case for all
![]() ,
,
![]() $\mathcal {F}\Vdash A$
.
$\mathcal {F}\Vdash A$
.
A formula A is a logical consequence of a set of formulas
![]() $\Gamma $
(notation
$\Gamma $
(notation
![]() $\Gamma \models A$
) just in case for all models
$\Gamma \models A$
) just in case for all models
![]() $\mathcal {M}$
and pairs
$\mathcal {M}$
and pairs
![]() $(m,h)\in MH(Tree)$
, if for all
$(m,h)\in MH(Tree)$
, if for all
![]() $B\in \Gamma $
,
$B\in \Gamma $
,
![]() $\mathcal {M}, (m,h)\vDash B$
, then
$\mathcal {M}, (m,h)\vDash B$
, then
![]() $\mathcal {M}, (m,h)\vDash A$
. As usual, we write
$\mathcal {M}, (m,h)\vDash A$
. As usual, we write
![]() $\models A$
if
$\models A$
if
![]() $\varnothing \models A$
and call A a logical truth.
$\varnothing \models A$
and call A a logical truth.
Since a picture says more than a thousand words, we give a simple graphical example of a (part of) a model.

Fig. 1 Simple example of a (single-agent) rich general stit-imagination episode model.
In Figure 1, the left side shows the imagination model, and the right side shows a content model. We are restricted to just one agent a. The thick rectangle is the moment m, which we have “zoomed into.” The thick lines represent (possibly empty) histories passing through moment m. There might also be other moments in them, which are not depicted here. The thin line dividing m represents that h and
![]() $h'$
are in different choice cells at m. The circles on the left side represent the neighborhoods assigned to the moment m and the respective histories h and
$h'$
are in different choice cells at m. The circles on the left side represent the neighborhoods assigned to the moment m and the respective histories h and
![]() $h'$
, which are attached to the respective circles. The dashed arrow is the accessibility relation between moment/history pairs, in this case the relation
$h'$
, which are attached to the respective circles. The dashed arrow is the accessibility relation between moment/history pairs, in this case the relation
![]() $R_{\Vert I_a (p)\Vert }$
between
$R_{\Vert I_a (p)\Vert }$
between
![]() $(m,h)$
and
$(m,h)$
and
![]() $(m,h')$
. In fact, we can see that
$(m,h')$
. In fact, we can see that
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! p$
for the only accessible pair,
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! p$
for the only accessible pair,
![]() $(m,h')$
makes
$(m,h')$
makes
![]() $\square p$
true (and, clearly,
$\square p$
true (and, clearly,
![]() $c(p)\sqsubseteq c (p)$
).
$c(p)\sqsubseteq c (p)$
).
The right side in the figure is a Hasse diagram for the partial order between
![]() $c(p)$
and
$c(p)$
and
![]() $c(q)$
.Footnote
26
So, the right side represents that
$c(q)$
.Footnote
26
So, the right side represents that
![]() $c(q)\sqsubseteq c(p)$
,
$c(q)\sqsubseteq c(p)$
,
![]() $c(p)\sqsubseteq c(p)$
and
$c(p)\sqsubseteq c(p)$
and
![]() $c(q)\sqsubseteq c(q)$
.
$c(q)\sqsubseteq c(q)$
.
Before addressing the (in)validities discussed by Berto, let us briefly introduce a principle that can only be formulated now that we have a unary imagination operator, an episodic imagination operator, and an operator encoding that something is in the agent’s mental image (or is imagined non-deliberately) namely
-
Imaginative Detachment (ID)
 $I_a A, A[a]\!\!\!\rightarrow \! B\models \square _a B.$
$I_a A, A[a]\!\!\!\rightarrow \! B\models \square _a B.$
This principle reads “If the agent deliberately imagines A and in deliberately imagining A, the agent imagines B, then the agent has B in their mental image.” Berto’s original operator could be seen as either encoding this in one go: “in imagining A, the agent imagines B,” or to encode the disposition of the agent to imagine B if they were to (deliberately) imagine A.
We consider ID to schematize situations in which an agent a deliberately imagines an input A, which then unfolds to output B under given constraints, where the latter is encoded by
![]() $A[a]\!\!\!\rightarrow \! B$
. If the agent deliberately imagines that they are in the mountains (
$A[a]\!\!\!\rightarrow \! B$
. If the agent deliberately imagines that they are in the mountains (
![]() $I_a p$
) and assuming that this unfolds to imagining that it is cold (
$I_a p$
) and assuming that this unfolds to imagining that it is cold (
![]() $p[a]\!\!\!\rightarrow \! q$
), they have it in their mental image that it is cold (
$p[a]\!\!\!\rightarrow \! q$
), they have it in their mental image that it is cold (
![]() $\square _a q$
). As opposed to Berto’s semantics, in which the agent can always only imagine B conditional on something else, we now have a way of expressing that the agent proceeds in the development of their mental image, without conditionalizing on some given input. Thus, besides other advantages, combining the language of Berto and that of Olkhovikov and Wansing, we have a way of describing an agent’s imaginative episode more precisely. In general, ID is not valid because
$\square _a q$
). As opposed to Berto’s semantics, in which the agent can always only imagine B conditional on something else, we now have a way of expressing that the agent proceeds in the development of their mental image, without conditionalizing on some given input. Thus, besides other advantages, combining the language of Berto and that of Olkhovikov and Wansing, we have a way of describing an agent’s imaginative episode more precisely. In general, ID is not valid because
![]() $\mathcal {M}, (m,h)\vDash I_a A $
does not guarantee that
$\mathcal {M}, (m,h)\vDash I_a A $
does not guarantee that
![]() $(m,h)R_{\Vert I_aA\Vert }(m,h)$
. For example, consider Figure 1 again: we have that
$(m,h)R_{\Vert I_aA\Vert }(m,h)$
. For example, consider Figure 1 again: we have that
![]() $\mathcal {M}, (m,h)\vDash I_a p$
and
$\mathcal {M}, (m,h)\vDash I_a p$
and
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! p$
but
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! p$
but
![]() $\mathcal {M}, (m,h)\nvDash \square _a p$
because
$\mathcal {M}, (m,h)\nvDash \square _a p$
because
![]() $\Vert p\Vert \notin N((m,h))$
. That is, although the agent imagines p in
$\Vert p\Vert \notin N((m,h))$
. That is, although the agent imagines p in
![]() $(m,h)$
(and, trivially, given they imagine p, they imagine p), they do not have p in their mental image at
$(m,h)$
(and, trivially, given they imagine p, they imagine p), they do not have p in their mental image at
![]() $(m,h)$
(but at
$(m,h)$
(but at
![]() $(m,h')$
).
$(m,h')$
).
This suggests that we can ensure that ID is valid in the class of models
![]() $\mathsf {M}$
such that for all models
$\mathsf {M}$
such that for all models
![]() $\mathcal {M} \in \mathsf {M}$
and all moment/history pairs
$\mathcal {M} \in \mathsf {M}$
and all moment/history pairs
![]() $(m,h)$
in
$(m,h)$
in
![]() $\mathcal {M}$
, if
$\mathcal {M}$
, if
![]() $\mathcal {M}, (m,h)\vDash I_a A$
, then
$\mathcal {M}, (m,h)\vDash I_a A$
, then
![]() $(m,h)R_{\Vert I_a p\Vert }(m,h)$
, that is, all moment/history pairs in which one deliberately imagines A are accessible via that imagining. Below, we formulate this in more structural terms as a (sufficient) condition on frames. Note that this does not make R reflexive in general and also that this doesn’t entail that what one imagines is true, i.e., it is still the case that
$(m,h)R_{\Vert I_a p\Vert }(m,h)$
, that is, all moment/history pairs in which one deliberately imagines A are accessible via that imagining. Below, we formulate this in more structural terms as a (sufficient) condition on frames. Note that this does not make R reflexive in general and also that this doesn’t entail that what one imagines is true, i.e., it is still the case that
![]() $I_a A\not \models A$
.
$I_a A\not \models A$
.
Let us now discuss Berto’s (in)validities and what our semantics makes of them.
5. Frame correspondences and (in)validities
5.1. Logical omni-imagination and hyperintensionality
Just as in Berto’s semantics, we can have episodic analogues of IVF-CVE by replacing
![]() $[A]B$
with
$[A]B$
with
![]() $A[a]\!\!\!\rightarrow \! B$
in each of eIVF-eCII from above. Each variant of these fails in our semantics.
$A[a]\!\!\!\rightarrow \! B$
in each of eIVF-eCII from above. Each variant of these fails in our semantics.
Proposition 5.18. The following do not hold in episodic stit-imagination logic: eIVF, eNIUF-in, eNIUF-out, eCVI, eCVE-in, eCVE-out, eCII.
Proof. The countermodels work just like in Berto’s semantics due to the content-condition.
In the next section we show that eCII corresponds to a frame condition. So, if one wants to have it around, one could.
As in Berto’s semantics, weak eCVE holds in our semantics, too, making the semantics not fully hyperintensional.
Proposition 5.19 (Weak eCVE-in)
If
![]() $\models A\equiv B$
and
$\models A\equiv B$
and
![]() $c(A)\sqsubseteq c(B)$
, then
$c(A)\sqsubseteq c(B)$
, then
![]() $(A[a]\!\!\!\rightarrow \! C)\models (B[a]\!\!\!\rightarrow \! C)$
.
$(A[a]\!\!\!\rightarrow \! C)\models (B[a]\!\!\!\rightarrow \! C)$
.
Proof. This is due to the fact that we index R by
![]() $\Vert I_a A\Vert $
(or
$\Vert I_a A\Vert $
(or
![]() $\Vert I_a B\Vert $
). Since it is the case that if
$\Vert I_a B\Vert $
). Since it is the case that if
![]() $\models A\equiv B$
, then
$\models A\equiv B$
, then
![]() $\models I_a A \equiv I_a B$
, see [Reference Wansing67], it follows that
$\models I_a A \equiv I_a B$
, see [Reference Wansing67], it follows that
![]() $\Vert I_a A\Vert $
=
$\Vert I_a A\Vert $
=
![]() $\Vert I_a B\Vert $
, and hence
$\Vert I_a B\Vert $
, and hence
![]() $R_{\Vert I_a A\Vert }= R_{\Vert I_a B\Vert }$
. So, the first conjunct of the condition is satisfied. Since
$R_{\Vert I_a A\Vert }= R_{\Vert I_a B\Vert }$
. So, the first conjunct of the condition is satisfied. Since
![]() $c(C)\sqsubseteq c(A)$
and
$c(C)\sqsubseteq c(A)$
and
![]() $c(A)\sqsubseteq c(B)$
,
$c(A)\sqsubseteq c(B)$
,
![]() $c(C)\sqsubseteq c(B)$
. So, the first conjunct of the truth-condition is satisfied.
$c(C)\sqsubseteq c(B)$
. So, the first conjunct of the truth-condition is satisfied.
We discuss this in more detail in Section 6.3.
5.2. Frame correspondence
With the semantics at hand, we now turn to presenting some frame correspondences, which allow us to drop conditions corresponding to debatable principles concerning imagination, such as PIE, or eIVF-eCII. Having desirable validities such as Success, Adjunction, and Addition and their corresponding frame conditions around, does not entail PIE or eCII.
To formulate structural frame conditions that correspond to formulas in our language, we structurally encode the voluntary imagination operator
![]() $I_a$
and the
$I_a$
and the
![]() $\square _a$
operator for each
$\square _a$
operator for each
![]() $a \in Ag$
. We do this defining the following two operations on sets of moment/history pairs:
$a \in Ag$
. We do this defining the following two operations on sets of moment/history pairs:
Definition 5.20. Let
![]() $X\subseteq MH(Tree)$
and
$X\subseteq MH(Tree)$
and
![]() $a\in Ag$
. Then
$a\in Ag$
. Then
-
•
 $\mathbb {I}_a X:=\lbrace (m,h)\in MH(Tree) | \forall h'(h'\in Choice^m_a(h) \Rightarrow X\in N_a((m,h')) \text { and }\exists h'\in H_m(X\not \in N_a((m,h'))))\rbrace $
and
$\mathbb {I}_a X:=\lbrace (m,h)\in MH(Tree) | \forall h'(h'\in Choice^m_a(h) \Rightarrow X\in N_a((m,h')) \text { and }\exists h'\in H_m(X\not \in N_a((m,h'))))\rbrace $
and -
•
 $m_a(X):=\lbrace (m,h) \mid X\in N_a((m,h))\rbrace $
.
$m_a(X):=\lbrace (m,h) \mid X\in N_a((m,h))\rbrace $
.
Lemma 5.21. Let
![]() $\mathcal {M}$
be a stit-imagination episode model. Then for all
$\mathcal {M}$
be a stit-imagination episode model. Then for all
![]() $a\in Ag$
and all formulas A of the language
$a\in Ag$
and all formulas A of the language
![]() $\mathcal {L}_{stit}$
:
$\mathcal {L}_{stit}$
:
![]() $\mathbb {I}_a \Vert A\Vert =\Vert I_a A\Vert $
and
$\mathbb {I}_a \Vert A\Vert =\Vert I_a A\Vert $
and
![]() $m_a(\Vert A\Vert )=\Vert \square _a (A)\Vert $
.
$m_a(\Vert A\Vert )=\Vert \square _a (A)\Vert $
.
Proof. By induction on the structure of formulas. We show for
![]() $\mathbb {I}_a$
the base case and the case for
$\mathbb {I}_a$
the base case and the case for
![]() $A:=[c]_a B$
.
$A:=[c]_a B$
.
If
![]() $A:=p$
, then
$A:=p$
, then
 $$ \begin{align*}&\mathbb{I}_a \Vert p\Vert\\ &=_{Def.5.20}\lbrace (m,h)\in MH(Tree) | \forall h'(h'\in Choice^m_a(h) \Rightarrow \Vert p\Vert\in N_a((m,h'))\\ &\quad \text{ and } \exists h'\in H_m(\Vert p\Vert \not\in N_a((m,h'))))\rbrace \\ &=_{Def.4.16}\lbrace (m,h)\in MH(Tree) | \mathcal{M}, (m,h)\vDash [c]_a \square_a p \text{ and } \mathcal{M}, (m,h)\vDash \neg S\square_a p\rbrace \\ &=_{Def. I_a}\lbrace (m,h)\in MH(Tree) | \mathcal{M}, (m,h)\vDash I_a p\rbrace \\ &=_{Def. \Vert.\Vert}\Vert I_a p\Vert \end{align*} $$
$$ \begin{align*}&\mathbb{I}_a \Vert p\Vert\\ &=_{Def.5.20}\lbrace (m,h)\in MH(Tree) | \forall h'(h'\in Choice^m_a(h) \Rightarrow \Vert p\Vert\in N_a((m,h'))\\ &\quad \text{ and } \exists h'\in H_m(\Vert p\Vert \not\in N_a((m,h'))))\rbrace \\ &=_{Def.4.16}\lbrace (m,h)\in MH(Tree) | \mathcal{M}, (m,h)\vDash [c]_a \square_a p \text{ and } \mathcal{M}, (m,h)\vDash \neg S\square_a p\rbrace \\ &=_{Def. I_a}\lbrace (m,h)\in MH(Tree) | \mathcal{M}, (m,h)\vDash I_a p\rbrace \\ &=_{Def. \Vert.\Vert}\Vert I_a p\Vert \end{align*} $$
If
![]() $A:=[c]_aB$
, then
$A:=[c]_aB$
, then
 $$ \begin{align*}&\mathbb{I}_a \Vert [c]_a B\Vert\\&=_{Def.5.20} \lbrace (m,h)\in MH(Tree) | \forall h'(h'\in Choice^m_a(h) \Rightarrow \Vert [c]_aB\Vert\in N_a((m,h')) \\ &\quad\text{ and } \exists h'\in H_m(\Vert [c]_aB\Vert \not\in N_a((m,h'))))\rbrace \\ &=_{Def.4.16}\lbrace (m,h)\in MH(Tree) | \mathcal{M}, (m,h)\vDash [c]_a \square_a [c]_a B\\ &\quad \text{ and }\mathcal{M}, (m,h)\vDash \neg S\square_a [c]_a B\rbrace\\ &=_{Def.I_a}\lbrace (m,h)\in MH(Tree) | \mathcal{M}, (m,h)\vDash I_a [c]_a B\rbrace\\ &=_{Def. \Vert.\Vert}\Vert I_a [c]_a B\Vert \\[-32pt] \end{align*} $$
$$ \begin{align*}&\mathbb{I}_a \Vert [c]_a B\Vert\\&=_{Def.5.20} \lbrace (m,h)\in MH(Tree) | \forall h'(h'\in Choice^m_a(h) \Rightarrow \Vert [c]_aB\Vert\in N_a((m,h')) \\ &\quad\text{ and } \exists h'\in H_m(\Vert [c]_aB\Vert \not\in N_a((m,h'))))\rbrace \\ &=_{Def.4.16}\lbrace (m,h)\in MH(Tree) | \mathcal{M}, (m,h)\vDash [c]_a \square_a [c]_a B\\ &\quad \text{ and }\mathcal{M}, (m,h)\vDash \neg S\square_a [c]_a B\rbrace\\ &=_{Def.I_a}\lbrace (m,h)\in MH(Tree) | \mathcal{M}, (m,h)\vDash I_a [c]_a B\rbrace\\ &=_{Def. \Vert.\Vert}\Vert I_a [c]_a B\Vert \\[-32pt] \end{align*} $$
We start by considering axiomatic analogues of the validities from Section 3 From here on, all proofs can be found in Appendix A.
Success
Proposition 5.22 (Success)
![]() $\mathcal {F} \Vdash A[a]\!\!\!\rightarrow \! A$
iff
$\mathcal {F} \Vdash A[a]\!\!\!\rightarrow \! A$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{suc}$
:
$\mathbb {C}_{suc}$
:
 $$ \begin{align*}&\forall a\in Ag\forall (m,h), (m,h')\in MH(Tree) \forall X\subseteq MH(Tree)((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow\\ &(m,h')\in m_a(X))\end{align*} $$
$$ \begin{align*}&\forall a\in Ag\forall (m,h), (m,h')\in MH(Tree) \forall X\subseteq MH(Tree)((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow\\ &(m,h')\in m_a(X))\end{align*} $$
For better readability of the conditions, from here on, we write the conditions as open formulas, although, strictly speaking, the conditions are the universal closures of the ones we formulate here.
Simplification
Proposition 5.23 (Simplification)
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
and
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
and
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! C)$
iff
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! C)$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{sim}$
:
$\mathbb {C}_{sim}$
:
 $$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y\cap Z)) \Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a (Y) \text{ and } (m,h')\in m_a (Z))]. \end{align*} $$
$$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y\cap Z)) \Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a (Y) \text{ and } (m,h')\in m_a (Z))]. \end{align*} $$
Adjunction
Proposition 5.24 (Adjunction)
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! B)\supset ((A[a]\!\!\!\rightarrow \! C)\supset (A[a]\!\!\!\rightarrow (B\wedge C)))$
iff
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! B)\supset ((A[a]\!\!\!\rightarrow \! C)\supset (A[a]\!\!\!\rightarrow (B\wedge C)))$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{adj}$
:
$\mathbb {C}_{adj}$
:
 $$ \begin{align*}&\forall (m,h)[\forall(m,h')((m,h)R_{\mathbb{I}_a X} (m,h') \Rightarrow ((m,h')\in m_a (Y) \text{ and } (m,h')\in m_a (Z))) \Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X} (m,h') \Rightarrow (m,h')\in m_a (Y\cap Z))].\end{align*} $$
$$ \begin{align*}&\forall (m,h)[\forall(m,h')((m,h)R_{\mathbb{I}_a X} (m,h') \Rightarrow ((m,h')\in m_a (Y) \text{ and } (m,h')\in m_a (Z))) \Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X} (m,h') \Rightarrow (m,h')\in m_a (Y\cap Z))].\end{align*} $$
Since we are modelling imaginative episodes as non-monotonic, it is worth considering some of the popular principles in the debate on non-monotonic reasoning [Reference Straßer, Antonelli and Zalta59]. Besides ST, whose analogue is Cautious Cut (see below), there is also the principle of Cautious Monotonicity.
Cautious Monotonicity
Proposition 5.25 (Cautious Monotonicity)
Let
![]() $\mathcal {F}$
be a frame.
$\mathcal {F}$
be a frame.
![]() $\mathcal {F} \Vdash ((A[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset ((A\wedge B)[a]\!\!\!\rightarrow \! C)$
iff
$\mathcal {F} \Vdash ((A[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset ((A\wedge B)[a]\!\!\!\rightarrow \! C)$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{cm}$
$\mathbb {C}_{cm}$
 $$ \begin{align*}&\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow ((m,h')\in m_a (Y) \text{ and } (m,h')\in m_a(Z)))\Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a (X\cap Y)} (m,h')\Rightarrow (m,h')\in m_a(Z))]. \end{align*} $$
$$ \begin{align*}&\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow ((m,h')\in m_a (Y) \text{ and } (m,h')\in m_a(Z)))\Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a (X\cap Y)} (m,h')\Rightarrow (m,h')\in m_a(Z))]. \end{align*} $$
Cautious Cut
Proposition 5.26 (Cautious Cut)
![]() $\mathcal {F}\Vdash (((A\wedge B) [a]\!\!\!\rightarrow \! C) \wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
iff
$\mathcal {F}\Vdash (((A\wedge B) [a]\!\!\!\rightarrow \! C) \wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{cc}$
:
$\mathbb {C}_{cc}$
:
 $$ \begin{align*}&\forall (m,h)[(\forall(m,h')((m,h)R_{\mathbb{I}_a(X\cap Y)} (m,h')\Rightarrow (m,h')\in m_a (Z))\ \&\ \\ &\forall(m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y)))\Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X} (m,h')\Rightarrow (m,h')\in m_a(Z))]. \end{align*} $$
$$ \begin{align*}&\forall (m,h)[(\forall(m,h')((m,h)R_{\mathbb{I}_a(X\cap Y)} (m,h')\Rightarrow (m,h')\in m_a (Z))\ \&\ \\ &\forall(m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y)))\Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X} (m,h')\Rightarrow (m,h')\in m_a(Z))]. \end{align*} $$
Substitutivity
For ease of notation, define the following:
Definition 5.27 (Set Selection Function)
Given a frame
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $X\subseteq MH(Tree)$
, we define
$X\subseteq MH(Tree)$
, we define
![]() $f(X, (m,h))=\lbrace (m, h') \in MH(Tree) | (m,h)R_X (m, h'))\rbrace $
.
$f(X, (m,h))=\lbrace (m, h') \in MH(Tree) | (m,h)R_X (m, h'))\rbrace $
.
Proposition 5.28 (Substitutivity)
![]() $\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! B)\wedge (B [a]\!\!\!\rightarrow \! A) \wedge (A[a]\!\!\!\rightarrow \! C) ) \supset B[a]\!\!\!\rightarrow \! C$
iff
$\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! B)\wedge (B [a]\!\!\!\rightarrow \! A) \wedge (A[a]\!\!\!\rightarrow \! C) ) \supset B[a]\!\!\!\rightarrow \! C$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{pie}$
:
$\mathbb {C}_{pie}$
:
 $$ \begin{align*}&(f(\mathbb{I}_a X, (m,h)) \subseteq m_a(Y)\ \&\ f(\mathbb{I}_a Y, (m,h)) \subseteq m_a(X)\ \&\ f(\mathbb{I}_a X, (m,h)) \subseteq m_a(Z)) \Rightarrow\\ &f(\mathbb{I}_a Y, (m,h)) \subseteq m_a(Z).\end{align*} $$
$$ \begin{align*}&(f(\mathbb{I}_a X, (m,h)) \subseteq m_a(Y)\ \&\ f(\mathbb{I}_a Y, (m,h)) \subseteq m_a(X)\ \&\ f(\mathbb{I}_a X, (m,h)) \subseteq m_a(Z)) \Rightarrow\\ &f(\mathbb{I}_a Y, (m,h)) \subseteq m_a(Z).\end{align*} $$
eCII
Proposition 5.29 (Closure under Episodically Imagined Implication)
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\supset C)) \supset ((A[a]\!\!\!\rightarrow \! B)\supset (A[a]\!\!\!\rightarrow \! C))$
iff
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\supset C)) \supset ((A[a]\!\!\!\rightarrow \! B)\supset (A[a]\!\!\!\rightarrow \! C))$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{CII}$
:
$\mathbb {C}_{CII}$
:
 $$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow ((m,h')\in m_a((MH(Tree)\setminus Y)\cup Z)\ \&\ \\ &(m,h')\in m_a(Y)) \Rightarrow \forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow (m,h')\in m_a(Z)))]. \end{align*} $$
$$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow ((m,h')\in m_a((MH(Tree)\setminus Y)\cup Z)\ \&\ \\ &(m,h')\in m_a(Y)) \Rightarrow \forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow (m,h')\in m_a(Z)))]. \end{align*} $$
The problematic principles in Berto’s semantics were his version of closure under imagined implication and ST. The principles in our semantics which are analogous to these are eCII and Cautious Cut. We can invalidate them by considering frames not satisfying the corresponding frame conditions. It has been pointed out, however, that Success and Simplification are plausible principles for imaginative episodes. Also Adjunction is reasonable to consider, despite our critical discussion above. So, ideally, our frames should satisfy
![]() $\mathbb {C}_{suc}$
,
$\mathbb {C}_{suc}$
,
![]() $\mathbb {C}_{sim}$
and, possibly,
$\mathbb {C}_{sim}$
and, possibly,
![]() $\mathbb {C}_{adj}$
but not validate eCII and Cautious Cut. For Cautious Cut, we can indeed show the following:
$\mathbb {C}_{adj}$
but not validate eCII and Cautious Cut. For Cautious Cut, we can indeed show the following:
Proposition 5.30. Let
![]() $\mathcal {F}$
be a frame. It is not the case that if
$\mathcal {F}$
be a frame. It is not the case that if
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{suc}$
,
$\mathbb {C}_{suc}$
,
![]() $\mathbb {C}_{sim}$
, and
$\mathbb {C}_{sim}$
, and
![]() $\mathbb {C}_{adj}$
, then
$\mathbb {C}_{adj}$
, then
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{cc}$
.
$\mathbb {C}_{cc}$
.
The axioms analogous to Simplification and Adjunction entail eCII, however.
Proposition 5.31. Let
![]() $\mathcal {F}$
be a frame such that
$\mathcal {F}$
be a frame such that
![]() $\mathcal {F} \Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
,
$\mathcal {F} \Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
,
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! C)$
, and
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! C)$
, and
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! B)\supset ((A[a]\!\!\!\rightarrow \! C)\supset (A[a]\!\!\!\rightarrow \! (B\wedge C)$
. Then
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! B)\supset ((A[a]\!\!\!\rightarrow \! C)\supset (A[a]\!\!\!\rightarrow \! (B\wedge C)$
. Then
![]() $\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! (B\supset C)) \supset ((A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C))$
.
$\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! (B\supset C)) \supset ((A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C))$
.
Of Simplification and Adjunction, the latter is the more debatable principle for imaginative episodes. As pointed out above, dismissing Simplification is not an option. So, if one wants to disregard eCII, Adjunction has to go, too.
We now turn to the invalidity of axioms analogous to the invalidities from Berto’s logic of imagination episodes. We establish these by constructing countermodels. Since the countermodels must be based on general frames, we have to define the element P of the general frames. In the following, given a frame
![]() $\mathcal {F}$
, we always define P as the powerset of all moment/history pairs of the frame’s tree:
$\mathcal {F}$
, we always define P as the powerset of all moment/history pairs of the frame’s tree:
![]() $P= \mathcal {P}(MH(Tree))$
. It is easy to see that this guarantees that P satisfies the conditions in Definition 4.14. Thus, we don’t mention P in the countermodels below. Except for Non-monotonicity and Indeterminacy, each of the countermodels works due to the content constraint. Thus, we omit graphical countermodels in these cases.
$P= \mathcal {P}(MH(Tree))$
. It is easy to see that this guarantees that P satisfies the conditions in Definition 4.14. Thus, we don’t mention P in the countermodels below. Except for Non-monotonicity and Indeterminacy, each of the countermodels works due to the content constraint. Thus, we omit graphical countermodels in these cases.
Indeterminacy
![]() $\not \models (A[a]\!\!\!\rightarrow \! (B\vee C))\supset ((A[a]\!\!\!\rightarrow \! B) \vee (A[a]\!\!\!\rightarrow \! C)).$
$\not \models (A[a]\!\!\!\rightarrow \! (B\vee C))\supset ((A[a]\!\!\!\rightarrow \! B) \vee (A[a]\!\!\!\rightarrow \! C)).$
We can, however, give a frame condition that corresponds to the axiomatic form of distribution over disjunction, namely:
Proposition 5.32 (Indeterminacy)
![]() $\mathcal {F}\Vdash A[a]\!\!\!\rightarrow \! (B\vee C)\supset ((A[a]\!\!\!\rightarrow \! B)\vee (A[a]\!\!\!\rightarrow \! C))$
iff
$\mathcal {F}\Vdash A[a]\!\!\!\rightarrow \! (B\vee C)\supset ((A[a]\!\!\!\rightarrow \! B)\vee (A[a]\!\!\!\rightarrow \! C))$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{ind}$
:
$\mathbb {C}_{ind}$
:
 $$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow m_a(Y\cup Z)) \Rightarrow \\ &(\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow m_a(Y)) \\ &\text{ or } \forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow m_a(Z)))]. \end{align*} $$
$$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow m_a(Y\cup Z)) \Rightarrow \\ &(\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow m_a(Y)) \\ &\text{ or } \forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow m_a(Z)))]. \end{align*} $$
Proof. Left as an exercise
Non-monotonicity
Proposition 5.33 (Non-monotonicity)
![]() $\not \models (A[a]\!\!\!\rightarrow \! B)\supset ((A\wedge C)[a]\!\!\!\rightarrow \! B)$
.
$\not \models (A[a]\!\!\!\rightarrow \! B)\supset ((A\wedge C)[a]\!\!\!\rightarrow \! B)$
.
Non-explosiveness
Proposition 5.34 (Non-explosion)
![]() $\not \models (A\wedge \neg A)[a]\!\!\!\rightarrow \! B$
.
$\not \models (A\wedge \neg A)[a]\!\!\!\rightarrow \! B$
.
Relevance
Proposition 5.35 (Relevance)
![]() $\not \models (A[a]\!\!\!\rightarrow \! B)\supset (A[a]\!\!\!\rightarrow \! (B\vee C))$
.
$\not \models (A[a]\!\!\!\rightarrow \! B)\supset (A[a]\!\!\!\rightarrow \! (B\vee C))$
.
We leave it as an exercise to provide frame conditions corresponding to the negation of the previous three invalidity statements, i.e., frame conditions corresponding to Monotonicity, Explosion, and Non-relevance.
No imaginative entailment
Proof. This is obvious.
Imaginative detachment
As aforementioned, having the entailment
![]() $I_a A, A[a]\!\!\!\rightarrow \! B\models \square _a B$
come out as valid seems desirable. A structural condition that is sufficient to ensure this is the following, given a frame
$I_a A, A[a]\!\!\!\rightarrow \! B\models \square _a B$
come out as valid seems desirable. A structural condition that is sufficient to ensure this is the following, given a frame
![]() $\mathcal {F}$
:
$\mathcal {F}$
:
-
 $\mathbb {C}_{ID}$
$\mathbb {C}_{ID}$
 $\forall (m,h)\in MH(Tree): (m,h)\in \mathbb {I}_a(X)\Rightarrow (m,h)R_{\mathbb {I}_a(X)}(m,h)$
.
$\forall (m,h)\in MH(Tree): (m,h)\in \mathbb {I}_a(X)\Rightarrow (m,h)R_{\mathbb {I}_a(X)}(m,h)$
.
That is, if we consider logical consequence defined as truth preservation over all moment/history pairs of all models based on frames satisfying
![]() $\mathbb {C}_{ID}$
to be
$\mathbb {C}_{ID}$
to be
![]() $\models _{ID}$
, then
$\models _{ID}$
, then
![]() $I_a A, A[a]\!\!\!\rightarrow \! B\models _{ID} \square _a B$
.
$I_a A, A[a]\!\!\!\rightarrow \! B\models _{ID} \square _a B$
.
Proof. Suppose
![]() $\mathcal {M}$
is based on
$\mathcal {M}$
is based on
![]() $\mathcal {F}$
satisfying
$\mathcal {F}$
satisfying
![]() $\mathbb {C}_{ID}$
and a)
$\mathbb {C}_{ID}$
and a)
![]() $\mathcal {M}, (m,h)\vDash I_a A$
and b)
$\mathcal {M}, (m,h)\vDash I_a A$
and b)
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! B$
. By
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! B$
. By
![]() $\mathbb {C}_{ID}$
and Lemma 5.21,
$\mathbb {C}_{ID}$
and Lemma 5.21,
![]() $(m,h)R_{\Vert I_a A\Vert } (m,h)$
. Hence, by b),
$(m,h)R_{\Vert I_a A\Vert } (m,h)$
. Hence, by b),
![]() $\Vert B\Vert \in N_a((m,h))$
and thus
$\Vert B\Vert \in N_a((m,h))$
and thus
![]() $\mathcal {M}, (m,h)\vDash \square _a B$
.
$\mathcal {M}, (m,h)\vDash \square _a B$
.
6. Discussion
Let us take stock and summarise what we have been doing so far, before we compare our semantics with other recent work on episodic imagination with voluntary input in [Reference Canavotto, Giordani and Berto15], and end this section with a summary of selected open problems.
6.1. Taking stock: advantages over Berto’s semantics
Based on Berto’s (possible worlds) semantics for episodic imagination and Wansing and Olkhovikov’s stit-logic for deliberate imagination, we have developed a new semantics that combines the two operators into a new imagination operator. This is intended to better model imaginative episodes in which the initial input is deliberately imagined.
We have discussed the (in)validities that were Berto’s main focus. The discussion showed that there are good reasons to claim that there are cases of ROMS (or “epistemically useful imagination” [Reference Badura, Kind, Badura and Kind4]) that invalidate prima facie plausible entailments such as Simplification or Addition. This motivated us to provide a semantics flexible enough to validate or invalidate them on purely semantic grounds. We have shown that we can recover all of Berto’s (in)validities. For the most important ones, we provided frame correspondence results, which offer a purely semantic way of adding or removing (un)desirable entailments. We consider this general and flexible approach a technical advantage over Berto’s semantics.
A particular advantage over Berto’s account is that we allow for counterexamples to closure under imagined implication, eCII. In epistemic logic, closure under known implication is one form of logical omniscience. And so, closure under imagined implication can be considered the imaginative analogue of this problem. Given the problem of bounded rationality [Reference Jago32, chap. 6], it is desirable to allow counterexamples to closure under imagined implication. This would require considering frames that don’t satisfy
![]() $\mathbb {C}_{CII}$
. Moreover, we have the possibility of adding Cautious Monotonicity by adding a frame condition. While Berto doesn’t discuss Cautious Monotonicity, it is a prominent principle in the literature on non-monotonic reasoning [Reference Straßer, Antonelli and Zalta59]. Thus, one might want to have it around for imagination, too. Similarly, we can invalidate Cautious Cut (analogue of Berto’s “Special Transitivity’). Berto considered Cautious Cut/ST as potentially problematic because “[i]t may be, however, that there are intuitive counterexamples to ST, forceful enough to lead us to reject PIE.” Since we index accessibility relations by truth-sets, we don’t have to add an analogue of PIE to ensure that conjunctions (disjunctions) in the initial input are commutative/associative. We consider this modularity of our semantics an advantage over Berto’s account. As shown above, our semantics also deals with all other problems of logical omni-imagination. By adding the content filter, introduced by Berto, we can also account for the failure of Adjunction and Addition.
$\mathbb {C}_{CII}$
. Moreover, we have the possibility of adding Cautious Monotonicity by adding a frame condition. While Berto doesn’t discuss Cautious Monotonicity, it is a prominent principle in the literature on non-monotonic reasoning [Reference Straßer, Antonelli and Zalta59]. Thus, one might want to have it around for imagination, too. Similarly, we can invalidate Cautious Cut (analogue of Berto’s “Special Transitivity’). Berto considered Cautious Cut/ST as potentially problematic because “[i]t may be, however, that there are intuitive counterexamples to ST, forceful enough to lead us to reject PIE.” Since we index accessibility relations by truth-sets, we don’t have to add an analogue of PIE to ensure that conjunctions (disjunctions) in the initial input are commutative/associative. We consider this modularity of our semantics an advantage over Berto’s account. As shown above, our semantics also deals with all other problems of logical omni-imagination. By adding the content filter, introduced by Berto, we can also account for the failure of Adjunction and Addition.
Despite our discussion of principles that are already prominently debated in the literature, having an episodic, a deliberate imagination operator, and a “mental imagery” operator in the language allows us to put forward a new entailment we called “imaginative detachment,” namely
![]() $I_a A,A[a]\!\!\!\rightarrow \! B\models \square _a B$
. This models the unfolding of an agent’s imagining under constraints. The formula involving the episodic imagination operator encodes the constraints on a given input and a possible output, while the formula involving the deliberate imagination operator expresses that the agent indeed deliberately imagines the input. We have provided a sufficient condition on frames to ensure that ID is valid. We consider this an increase in expressive power, which is desirable if one wants to model that an imaginative episode unfolds.
$I_a A,A[a]\!\!\!\rightarrow \! B\models \square _a B$
. This models the unfolding of an agent’s imagining under constraints. The formula involving the episodic imagination operator encodes the constraints on a given input and a possible output, while the formula involving the deliberate imagination operator expresses that the agent indeed deliberately imagines the input. We have provided a sufficient condition on frames to ensure that ID is valid. We consider this an increase in expressive power, which is desirable if one wants to model that an imaginative episode unfolds.
Although this subsection’s title is solely referring to Berto’s semantics, let us briefly say a few words concerning Olkhovikov and Wansing’s logic, too. As their semantics models deliberate imagination only, we have extended on their approach by adding an episodic operator. Moreover, the deliberate imagination operator validates CVE, that is, if A and B are classically equivalent, so are
![]() $I_aA$
and
$I_aA$
and
![]() $I_a B$
. In combination with Berto’s truth-condition for the episodic imagination opertaor, this results in our semantics validating weak eCVE-in. We discuss this principle below in Section 6.3
$I_a B$
. In combination with Berto’s truth-condition for the episodic imagination opertaor, this results in our semantics validating weak eCVE-in. We discuss this principle below in Section 6.3
So, in sum, our semantics has increased the expressive power by combining two formal languages, thereby taking into account that imaginative episodes involve deliberate imaginings and that these unfold under some constraints. This has given us a way of expressing a feature of imaginative episodes, ID, that wasn’t expressible before. Moreover, the technical advantage of having a frame correspondence allows us to systematically add or remove desirable or undesirable entailments, based on one’s favourite theory of imagination.
Leaving Berto’s, and Wansing and Olkhovikov’s logics, let us compare our semantics to another agentive approach to the logic of imagination.
6.2. Discussion of Canavotto et al.’s logic [Reference Canavotto, Giordani and Berto15]
There is other recent work on combining Berto’s account with a formal model of agency by Canavotto et al. [Reference Canavotto, Giordani and Berto15], henceforth CGB. Their models are multi-relational Kripke models composed of a non-empty set of possible worlds, a function that assigns a topic-model (content-model) to each world, a function R, used to interpret their agentive modality, three families of functions, and a valuation. Their semantics is meant to model ROMS and it is emphasizing (a) that the imagining agent has certain options to imagine (about), and (b) imaginative episodes come with an overall topic. How does their approach compare to ours? It is beyond the scope of the present (already long) paper to give a full-fledged and in-depth comparison between our and their semantics. We will thus briefly introduce their formalism, and emphasize three aspects that demand further investigation for tipping the scales between the two semantics. In general, we consider the two semantics to be concerned with slightly different aspects of ROMS.
For better comparison, let us briefly rehearse CGB’s central definitions (we adapted notation).
Definition 6.36 (Language CGB)
The language has a countable set of variables for atomic propositions
![]() $Var_P=\lbrace p_i,q_i, r_i\rbrace _{i\in \mathbb {N}}$
, a countable set of content variables
$Var_P=\lbrace p_i,q_i, r_i\rbrace _{i\in \mathbb {N}}$
, a countable set of content variables
![]() $Var_C=\lbrace t_i\rbrace _{i\in \mathbb {N}}$
and a singleton set
$Var_C=\lbrace t_i\rbrace _{i\in \mathbb {N}}$
and a singleton set
![]() $Ag=\lbrace a\rbrace $
having one agent as a single element (we also use a as an agent name in the formulas). The set of formulas
$Ag=\lbrace a\rbrace $
having one agent as a single element (we also use a as an agent name in the formulas). The set of formulas
![]() $Form$
is given by the following Backus–Naur grammar:
$Form$
is given by the following Backus–Naur grammar:
where
![]() $P\in Var_P$
,
$P\in Var_P$
,
![]() $\tau \in Var_C$
, and other propositional connectives and dual operators for the modalities. The philosophical interpretation of the operators is as follows (negation and conjunction are classical, and
$\tau \in Var_C$
, and other propositional connectives and dual operators for the modalities. The philosophical interpretation of the operators is as follows (negation and conjunction are classical, and
![]() $\square A$
is an S5-modality interpreted as unrestricted necessity):
$\square A$
is an S5-modality interpreted as unrestricted necessity):
-
1.
 $[a]$
is an agentive modality. It represents the imaginative options of agent
$[a]$
is an agentive modality. It represents the imaginative options of agent
 $a$
. We read
$a$
. We read
 $[a]A$
as saying that A is true at all worlds that are like the current one, up to the content imagined by
$[a]A$
as saying that A is true at all worlds that are like the current one, up to the content imagined by
 $a$
given an input [our emph.].
$a$
given an input [our emph.]. -
2.
 $[im_{A}]$
picks out a set of worlds, selected given input A. We read
$[im_{A}]$
picks out a set of worlds, selected given input A. We read
 $[im_{A}]B$
as saying that given A, the agent imagines that B, [
$[im_{A}]B$
as saying that given A, the agent imagines that B, [
 $\ldots $
] independently of the selected topic. This corresponds to the original operator considered in [Reference Berto9].
$\ldots $
] independently of the selected topic. This corresponds to the original operator considered in [Reference Berto9]. -
3.
 $[im^{\tau }_{A}]$
also takes topics into account: it picks out a set of worlds, selected given input A and topic
$[im^{\tau }_{A}]$
also takes topics into account: it picks out a set of worlds, selected given input A and topic
 $\tau $
. We read
$\tau $
. We read
 $[im^{\tau }_{A}]B$
as saying that given A and
$[im^{\tau }_{A}]B$
as saying that given A and
 $\tau $
, the agent imagines that B [
$\tau $
, the agent imagines that B [
 $\ldots $
]
$\ldots $
] -
4.
 $[\approx ^{\tau }_{A}]$
picks out the worlds indistinguishable from the current one, given input A and topic
$[\approx ^{\tau }_{A}]$
picks out the worlds indistinguishable from the current one, given input A and topic
 $\tau $
. We read
$\tau $
. We read
 $[im^{\tau }_{A}]B$
as saying that B is true in all worlds which are like the current one given A and
$[im^{\tau }_{A}]B$
as saying that B is true in all worlds which are like the current one given A and
 $\tau $
[
$\tau $
[
 $\ldots $
][Reference Canavotto, Giordani and Berto15, pp.7–8, notation adjusted].
$\ldots $
][Reference Canavotto, Giordani and Berto15, pp.7–8, notation adjusted].
Definition 6.37 (CGB-Models)
A CGB-model is a tuple
where
![]() $w\in W, A\in Form, \tau \in Var_T$
, and:
$w\in W, A\in Form, \tau \in Var_T$
, and:
-
•
 $W\neq \varnothing $
.
$W\neq \varnothing $
. -
• For each
 $w\in W$
,
$w\in W$
,
 $\mathcal {C}_w=\langle \textsf {C}_w, \oplus _w, c_w\rangle $
is a content model. (We write
$\mathcal {C}_w=\langle \textsf {C}_w, \oplus _w, c_w\rangle $
is a content model. (We write
 $\sqsubseteq _w$
for the partial order defined from
$\sqsubseteq _w$
for the partial order defined from
 $\oplus _w$
).
$\oplus _w$
). -
•
 $R: W\longrightarrow \mathcal {P}(W)$
is a function, in particular, an equivalence relation. Intuitively, given some input and content,
$R: W\longrightarrow \mathcal {P}(W)$
is a function, in particular, an equivalence relation. Intuitively, given some input and content,
 $R(w)$
selects the worlds that are like w up to the content given the input, and thus offers different imaginative options for the agent.
$R(w)$
selects the worlds that are like w up to the content given the input, and thus offers different imaginative options for the agent. -
• For each
 $A\in Form$
,
$A\in Form$
,
 $C_{A}: W\longrightarrow \mathcal {P}(W)$
is a set-selection function as used in [Reference Berto9].
$C_{A}: W\longrightarrow \mathcal {P}(W)$
is a set-selection function as used in [Reference Berto9]. -
• For each
 $A\in Form$
,
$A\in Form$
,
 $\tau \in Var_T$
,
$\tau \in Var_T$
,
 $C_{A}^{\tau }: W\longrightarrow \mathcal {P}(W)$
,
$C_{A}^{\tau }: W\longrightarrow \mathcal {P}(W)$
,
 $C_{A}^{\tau }(w)$
is a partition on
$C_{A}^{\tau }(w)$
is a partition on
 $C_{A}(w)$
, representing what the agent imagines in w, given A and
$C_{A}(w)$
, representing what the agent imagines in w, given A and
 $\tau $
.
$\tau $
. -
• For each
 $A\in Form$
,
$A\in Form$
,
 $\tau \in Var_T$
,
$\tau \in Var_T$
,
 $I_{A}^{\tau }: W\longrightarrow \mathcal {P}(W)$
is a choice function such that if
$I_{A}^{\tau }: W\longrightarrow \mathcal {P}(W)$
is a choice function such that if
 $w '\in C_{A}(w)$
,
$w '\in C_{A}(w)$
,
 $I^{\tau }_{A}(w')$
selects the equivalence class of
$I^{\tau }_{A}(w')$
selects the equivalence class of
 $w'$
in the partition induced by
$w'$
in the partition induced by
 $\tau $
on
$\tau $
on
 $C_{\tau }(w)$
.
$C_{\tau }(w)$
. -
•
 $v: Var_p\longrightarrow \mathcal {P}(W)$
is a standard valuation function.
$v: Var_p\longrightarrow \mathcal {P}(W)$
is a standard valuation function.
For an elaborate explanation of the various functions, their interactions, and their philosophical motivation, using a pictorial example, see the original paper [Reference Canavotto, Giordani and Berto15]. There are several conditions imposed on the models that ensure the functions behave as intended. Again, we refer the reader to the original paper for the details (pp. 13–14 are especially relevant).
Definition 6.38 (Truth in a world in a model)
Given
![]() $\mathcal {M}$
is a CGB model and w is a world in
$\mathcal {M}$
is a CGB model and w is a world in
![]() $\mathcal {M}$
, truth at w in
$\mathcal {M}$
, truth at w in
![]() $\mathcal {M}$
is defined inductively as follows:
$\mathcal {M}$
is defined inductively as follows:
 $$ \begin{align*} &\mathcal{M}, w\vDash p\Leftrightarrow w\in v(p)\\ &\mathcal{M}, w\vDash \neg A\Leftrightarrow \mathcal{M}, w\nvDash A\\ &\mathcal{M}, w\vDash A \wedge B \Leftrightarrow \mathcal{M}, w\vDash A\ \&\ \mathcal{M}, w\vDash B\\ &\mathcal{M}, w\vDash \square A\Leftrightarrow \forall v\in w: \mathcal{M}, v\vDash A\\ &\mathcal{M}, w\vdash [a]A \Leftrightarrow \forall v(v\in R(w)\Rightarrow \mathcal{M}, v\vDash A)\\ &\mathcal{M}, w\vDash [im_{A}]B\Leftrightarrow \forall v(v\in C_{A}(w)\Rightarrow \mathcal{M}, v\vDash B)\ \&\ c_w(B)\sqsubseteq_w c_w(A)\\ &\mathcal{M}, w\vDash [im_{A}^{\tau}]B\Leftrightarrow \forall v(v\in C_{A}^{\tau}(w)\Rightarrow \mathcal{M}, v\vDash B)\ \&\ c_w(B)\sqsubseteq_w c_w(A)\\ &\mathcal{M}, w\vDash [\approx_{A}^{\tau}]A\Leftrightarrow \forall v(v\in I_{A}^{\tau}(w)\Rightarrow \mathcal{M}, v\vDash B). \end{align*} $$
$$ \begin{align*} &\mathcal{M}, w\vDash p\Leftrightarrow w\in v(p)\\ &\mathcal{M}, w\vDash \neg A\Leftrightarrow \mathcal{M}, w\nvDash A\\ &\mathcal{M}, w\vDash A \wedge B \Leftrightarrow \mathcal{M}, w\vDash A\ \&\ \mathcal{M}, w\vDash B\\ &\mathcal{M}, w\vDash \square A\Leftrightarrow \forall v\in w: \mathcal{M}, v\vDash A\\ &\mathcal{M}, w\vdash [a]A \Leftrightarrow \forall v(v\in R(w)\Rightarrow \mathcal{M}, v\vDash A)\\ &\mathcal{M}, w\vDash [im_{A}]B\Leftrightarrow \forall v(v\in C_{A}(w)\Rightarrow \mathcal{M}, v\vDash B)\ \&\ c_w(B)\sqsubseteq_w c_w(A)\\ &\mathcal{M}, w\vDash [im_{A}^{\tau}]B\Leftrightarrow \forall v(v\in C_{A}^{\tau}(w)\Rightarrow \mathcal{M}, v\vDash B)\ \&\ c_w(B)\sqsubseteq_w c_w(A)\\ &\mathcal{M}, w\vDash [\approx_{A}^{\tau}]A\Leftrightarrow \forall v(v\in I_{A}^{\tau}(w)\Rightarrow \mathcal{M}, v\vDash B). \end{align*} $$
Logical consequence is defined as usual as truth-preservation over all worlds.
First, let us look at some of the (in)validities we have discussed above. CGB provide a sound and complete axiomatisation, which includes, among others, the following:
 $$ \begin{align*} &[im^{\tau}_{A}]1: ([im^{\tau}_{A}]B\wedge [im^{\tau}_{A}]C)\supset [im^{\tau}_{A}](B\wedge C),\\ &[im^{\tau}_{A}]2: ([im^{\tau}_{A}]B\wedge [im^{\tau}_{A}](B\supset C)\supset [im^{\tau}_{A}]C. \end{align*} $$
$$ \begin{align*} &[im^{\tau}_{A}]1: ([im^{\tau}_{A}]B\wedge [im^{\tau}_{A}]C)\supset [im^{\tau}_{A}](B\wedge C),\\ &[im^{\tau}_{A}]2: ([im^{\tau}_{A}]B\wedge [im^{\tau}_{A}](B\supset C)\supset [im^{\tau}_{A}]C. \end{align*} $$
These are just Adjunction and eCII, both of which, we have argued, might be considered invalid, even in the case of ROMS. So, our semantics’ advantage of higher flexibility we mentioned in comparison with Berto applies here, too.
Moreover, we think that our semantics really takes into account that the agent deliberately chooses to imagine the initial input of an imaginative episode (which we have already pointed out above), while CGB’s account doesn’t. First, note that
![]() $[a]$
behaves like a cstit-modality for it quantifies over all worlds from a selected set of choices. That is, it is not a deliberate choice operator, although, such an operator could be defined in their setting as usual by
$[a]$
behaves like a cstit-modality for it quantifies over all worlds from a selected set of choices. That is, it is not a deliberate choice operator, although, such an operator could be defined in their setting as usual by
![]() $[a]_d A:=[a]A\wedge \neg \square A$
. (Remember this because we’ll discuss it below.) Note that this is a standard definition to define deliberate choice from non-deliberate choice in logics of agency, see, e.g., [Reference Belnap, Perloff and Xu6].
$[a]_d A:=[a]A\wedge \neg \square A$
. (Remember this because we’ll discuss it below.) Note that this is a standard definition to define deliberate choice from non-deliberate choice in logics of agency, see, e.g., [Reference Belnap, Perloff and Xu6].
Now, consider one of their bridge axioms:
![]() $[im_{A}]B \leftrightarrow [a][im_{A}^{\tau }]B$
. This is meant to tell us that the agent imagines B given A just in case the agent non-deliberately chooses to imagine B given A and
$[im_{A}]B \leftrightarrow [a][im_{A}^{\tau }]B$
. This is meant to tell us that the agent imagines B given A just in case the agent non-deliberately chooses to imagine B given A and
![]() $\tau $
. This does not express that the agent is deliberately imagining A, which is the initial input. So, would it be possible to express the deliberate imagining in terms of the previously defined deliberate choice operator? To investigate this, we note that CGB add a condition ensuring Success:
$\tau $
. This does not express that the agent is deliberately imagining A, which is the initial input. So, would it be possible to express the deliberate imagining in terms of the previously defined deliberate choice operator? To investigate this, we note that CGB add a condition ensuring Success:
![]() $\models _{CGB} [im_{A}]A$
and
$\models _{CGB} [im_{A}]A$
and
![]() $\models _{CGB}[im_{A}^{\tau }] A$
. That means that
$\models _{CGB}[im_{A}^{\tau }] A$
. That means that
![]() $\models _{CGB}\square [im_{A}^{\tau }] A$
but this means that
$\models _{CGB}\square [im_{A}^{\tau }] A$
but this means that
![]() $[a]_d[im_{A}^{\tau }] A$
is unsatisfiable. That is, the agent can never deliberately choose to imagine the input, at least if we aimed to express that the agent chooses to imagine A by
$[a]_d[im_{A}^{\tau }] A$
is unsatisfiable. That is, the agent can never deliberately choose to imagine the input, at least if we aimed to express that the agent chooses to imagine A by
![]() $[a][im_{A}^{\tau }]A$
, which warrants formalising that the agent deliberately chooses to imagine
$[a][im_{A}^{\tau }]A$
, which warrants formalising that the agent deliberately chooses to imagine
![]() $A$
by
$A$
by
![]() $[a]_d[im_{A}^{\tau }]A$
. (After all, why would deliberately choosing to imagine be formalised differently than choosing to imagine?) This means that it doesn’t really make sense to formalise “the agent imagines B given they deliberately imagine A” as
$[a]_d[im_{A}^{\tau }]A$
. (After all, why would deliberately choosing to imagine be formalised differently than choosing to imagine?) This means that it doesn’t really make sense to formalise “the agent imagines B given they deliberately imagine A” as
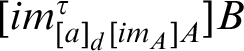 $[im^{\tau }_{[a]_d[im_{A}]A}]B$
because the subscript is an unsatisfiable formula expressing the assumption that the agent deliberately imagines A. This makes it, prima facie, difficult to express ID as well because that would require that it is possible to express that the agent deliberately imagines the initial input, which is, as we just argued, not expressible in the straightforward way by
$[im^{\tau }_{[a]_d[im_{A}]A}]B$
because the subscript is an unsatisfiable formula expressing the assumption that the agent deliberately imagines A. This makes it, prima facie, difficult to express ID as well because that would require that it is possible to express that the agent deliberately imagines the initial input, which is, as we just argued, not expressible in the straightforward way by
![]() $[a]_d[im_{A}]A$
. And, as we argued above, ID expresses the actual performance of an imaginative episode with voluntary input, or an imaginative episode with deliberately chosen input. It is left as an open issue how to incorporate the idea that the agent deliberately chooses to imagine the initial input into CGB’s account.
$[a]_d[im_{A}]A$
. And, as we argued above, ID expresses the actual performance of an imaginative episode with voluntary input, or an imaginative episode with deliberately chosen input. It is left as an open issue how to incorporate the idea that the agent deliberately chooses to imagine the initial input into CGB’s account.
In light of this short presentation of their account of agency, it is worth noting that the use of Kripke semantics for agentive operators might be formally justified (as [Reference Ciuni and Lorini23] show how to translate stit-semantics into multi-relational Kripke semantics and vice versa). It might, however, lack some of the underlying philosophical motivation. The stit-framework has been developed on a solid philosophical foundation by [Reference Belnap, Perloff and Xu6]. A discussion of this issue is beyond the scope of this paper but it is worth having to tip the philosophical scales in favor of one of the semantics.
There are two further points worth mentioning in comparison. One of the central contributions of our work are structural frame correspondences. This is not present in [Reference Canavotto, Giordani and Berto15]. They still work with conditions on models. This shows that our account has an advantage from a methodological point of view and provides additional formal results, lacking in their account. It speaks in their favor, however, that they have a sound and complete axiomatisation. We are confident that the methods they use to deal with contents/topics can be combined with the completeness proof from [Reference Olkhovikov and Wansing48, Reference Olkhovikov and Wansing49]. Given a canonical model construction and the canonical model satisfies the respective frame property, the correspondence theory would make it straightforward to establish completeness for the various logics resulting from the respective principles concerning imaginative episodes with voluntary input.
Finally, they point out that they don’t model the temporal aspect of an imaginative episode. Neither does our semantics. Their framework requires an additional accessibility relation (or some other formal tool) for adding temporal modalities, however. The branching time structures of stit-logic we use are already intended to model agency over time and thus lend themselves to the introduction of temporal modalities. Indeed, [Reference Belnap, Perloff and Xu6] combines stit-modalities and temporal modalities. So, our framework might be more promising in this respect. Again, modelling agency over time via Kripke semantics might be formally justified as evident from [Reference Ciuni and Lorini23] but the philosophical foundation might be lacking. Not so for a stit-temporal account à la [Reference Belnap, Perloff and Xu6].
Summing up our brief discussion of Canavotto et al. [Reference Canavotto, Giordani and Berto15], we conclude that the following issues need to be addressed in-depth:
-
1. as opposed to CGB’s approach, our semantics is flexible in adding/removing (un)desirable (in)validities, that is, our approach is more general;
-
2. in CGB’s approach, it is not prima facie clear how to express that the agent deliberately imagines the initial input, thereby not having a straightforward analogue of ID (which is a desirable principle);
-
3. on conceptual grounds and based on the philosophical motivation for the semantics, our branching-time structures enriched by neighborhoods might be preferable over CGB’s Kripke semantics, although it might be possible to translate one into the other on purely formal grounds; and
-
4. as imaginative episodes expand over time, branching-time structures offer a natural framework for adding temporal operators.
Granting that our discussion has been rather brief and that some of these issues might be resolved, we still conclude tentatively, that our approach is preferable over CGB’s.
6.3. Open problem: weak eCVE-in
Let us briefly point towards one open problem of Berto’s, CGB’s, and our semantics, namely weak closure under equivalent formulas in the input.Footnote 27 Roughly put, the problem is, in general, that if two formulas A and B are equivalent and the content of B is included in the content of A, then imagining C given one deliberately imagines B entails that one imagines C given one deliberately imagines A. Pierre Saint-Germier has presented the following example to motivate that this constitutes a problem:
Ted is a person who eats well, goes to the gym twice a week and sleeps eight hours every night. The only thing that prevents his lifestyle from being really healthy is that he drinks a whole bottle of Cognac every day for breakfast. As I imagine that Ted does not drink alcohol, I imagine ceteris paribus that he lives a healthy life. But as I imagine that Ted does not drink alcohol, or he does not drink alcohol but takes heroin, I do not imagine ceteris paribus that he lives a healthy life. For it is consistent with what I imagine that he may take heroin and this is not healthy at all. [Reference Saint-Germier, Giordani and Malinowski56, p. 89]
So, if we let p stand for “Ted does not drink alcohol,” q for “Ted lives a healthy life,” and r for “Ted takes heroin,” we have it that
![]() $[p]q$
but
$[p]q$
but
![]() $\neg [p\vee (p\wedge r)]q$
. Saint-Germier’s proof that this holds in Berto’s semantics involves reference to PIE and Success. He concludes that PIE is the culprit and proposes a truthmaker semantics for imaginative episodes. Discussing the truthmaker approach is beyond the scope of this paper but since Saint-Germier is only concerned with modelling Berto’s episodic imagination operator, it is fair to say that it does not model agentive aspects of imagination and hence does not allow formulating ID. It also validates most of the principles which we have argued to be debatable. So, again, our approach is more flexible.
$\neg [p\vee (p\wedge r)]q$
. Saint-Germier’s proof that this holds in Berto’s semantics involves reference to PIE and Success. He concludes that PIE is the culprit and proposes a truthmaker semantics for imaginative episodes. Discussing the truthmaker approach is beyond the scope of this paper but since Saint-Germier is only concerned with modelling Berto’s episodic imagination operator, it is fair to say that it does not model agentive aspects of imagination and hence does not allow formulating ID. It also validates most of the principles which we have argued to be debatable. So, again, our approach is more flexible.
How problematic is the example, though? We think the example rests on an inadequate formalisation of what exactly the imaginative episodes are. When given a disjunction as initial input of an imaginative episode, it is not clear that we imagine the disjunction as a whole, that is, we do not necessarily consider the case in which both disjuncts are true. Instead, we tend to treat it as an exclusive disjunction and evaluate each disjunct seperately. This is evidenced by research on the evaluation of conditionals [Reference Ciardelli, Zhang and Champollion22], which involves imaginative episodes in the form of ROMS, that is, one imagines the antecedent and evaluates the consequent in one’s imagination. As Ciardelli et al. [Reference Ciardelli, Zhang and Champollion22] interpret their results, in evaluating conditionals with disjunctive antecedents, subjects evaluate each disjunct seperately in their imagination. If this is right, then formalising the scenario involving Ted as
![]() $[p]q$
but
$[p]q$
but
![]() $\neg [p\vee (p\wedge r)]q$
seems inadequate. Rather, it seems,
$\neg [p\vee (p\wedge r)]q$
seems inadequate. Rather, it seems,
![]() $[p]q$
but
$[p]q$
but
![]() $\neg [p\wedge r]q$
, which is fine, given the episodic imagination operator of Berto’s is non-monotonic (and so is ours, i.e.,
$\neg [p\wedge r]q$
, which is fine, given the episodic imagination operator of Berto’s is non-monotonic (and so is ours, i.e.,
![]() $p[a]\!\!\!\rightarrow \! q$
and
$p[a]\!\!\!\rightarrow \! q$
and
![]() $\neg ((p\wedge r)[a]\!\!\!\rightarrow \! q)$
). So, whether weak eCVE-in is a serious problem seems to depend on better understanding how we imagine disjunctions. If it was found that usually we don’t imagine disjunctions as inputs but rather each disjunct constitutes its own imaginative episode where it features as initial input, then Saint-Germier’s argument would rest on an inadequate formalisation and thus would not be successful in showing that weak eCVE-in is problematic.
$\neg ((p\wedge r)[a]\!\!\!\rightarrow \! q)$
). So, whether weak eCVE-in is a serious problem seems to depend on better understanding how we imagine disjunctions. If it was found that usually we don’t imagine disjunctions as inputs but rather each disjunct constitutes its own imaginative episode where it features as initial input, then Saint-Germier’s argument would rest on an inadequate formalisation and thus would not be successful in showing that weak eCVE-in is problematic.
7. Conclusion
We have improved on Berto’s initial account by (i) modelling the deliberate choice of the initial input of an imaginative episode (ii) in a multi-agent setting, (iii) providing structural correspondence results, which (iv) allows counterexamples to potentially problematic axioms. We have also pointed out some advantages of our semantics compared to recent work by Canavaotto et al. who also aim to model agentive imagination. As opposed to their account, our approach takes seriously the idea that imaginers deliberately choose the initial input of their imaginings. We argued that taking this seriously is grounded in accepting the principle ID, namely that deliberately imagining some input A, the fact that given this input one imagines B, this entails that one (non-deliberately) imagines B (or has B in one’s mental image). This principle is desirable because it expresses the actual performance of an imaginative episode.
For future work, the following remains. On the more philosophical side, for an adequate model of imaginative episodes, the consideration of background beliefs and background knowledge needs to be integrated. Second, there is a temporal component to imaginative episodes. Since we use branching time structures, adding temporal modalities looks promising, although it is known that this generates complexity and decidability issues [Reference Belnap, Perloff and Xu6]. Finally, we have discussed a problem raised by Saint-Germier concerning the substitution of logically equivalent formulas in the input of imaginative episodes. We argued that whether this poses a problem depends on how to formalise imaginative episodes in which the agent imagines a disjunction.
On the formal side, developing a sound and complete axiomatisation, sequent calculus, or tableau system for our semantics is desirable. Using labelled sequent calculi [Reference Negri and Pavlović45] seems promising. Moreover, the decidability of the logic is an open issue. An extension of the propositional stit-logic for imagination episodes with voluntary input to the first-order level is of both philosophical and formal interest. Especially, since, to the best of our knowledge, there is no first-order stit semantics.
A. Proofs
Success
Proposition 5.22.
![]() $\mathcal {F} \Vdash A[a]\!\!\!\rightarrow \! A$
iff
$\mathcal {F} \Vdash A[a]\!\!\!\rightarrow \! A$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{suc}$
:
$\mathbb {C}_{suc}$
:
 $$ \begin{align*}&\forall a\in Ag\forall (m,h), (m,h')\in MH(Tree) \forall X\subseteq MH(Tree)((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow\\ &(m,h')\in m_a(X)).\end{align*} $$
$$ \begin{align*}&\forall a\in Ag\forall (m,h), (m,h')\in MH(Tree) \forall X\subseteq MH(Tree)((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow\\ &(m,h')\in m_a(X)).\end{align*} $$
Proof. Suppose
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{suc}$
. Let
$\mathbb {C}_{suc}$
. Let
![]() $\mathcal {M}$
be a general imagination episode model based on
$\mathcal {M}$
be a general imagination episode model based on
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $(m,h)$
be in
$(m,h)$
be in
![]() $\mathcal {M}$
. Assume
$\mathcal {M}$
. Assume
![]() $(m,h')\in H_m$
and
$(m,h')\in H_m$
and
![]() $(m,h)R_{\Vert I_a A \Vert }(m,h')$
. By Lemma 5.21,
$(m,h)R_{\Vert I_a A \Vert }(m,h')$
. By Lemma 5.21,
![]() $(m,h)R_{\mathbb {I}_a\Vert A\Vert }(m,h')$
. We need to show that
$(m,h)R_{\mathbb {I}_a\Vert A\Vert }(m,h')$
. We need to show that
![]() $\mathcal {M}, (m,h')\vDash \square _a A$
. By
$\mathcal {M}, (m,h')\vDash \square _a A$
. By
![]() $\mathbb {C}_{suc}$
, it follows that
$\mathbb {C}_{suc}$
, it follows that
![]() $(m,h')\in m_a(\Vert A\Vert )$
. By Lemma 5.21,
$(m,h')\in m_a(\Vert A\Vert )$
. By Lemma 5.21,
![]() $(m,h')\in \Vert \square _a A\Vert .$
Hence, by the definition of truth-sets,
$(m,h')\in \Vert \square _a A\Vert .$
Hence, by the definition of truth-sets,
![]() $\mathcal {M}, (m,h')\vDash \square _a A$
. Since the logical vocabulary is content-transparent,
$\mathcal {M}, (m,h')\vDash \square _a A$
. Since the logical vocabulary is content-transparent,
![]() $c(\square _a A)\sqsubseteq c(I_a A)$
.
$c(\square _a A)\sqsubseteq c(I_a A)$
.
Suppose
![]() $\mathcal {F}$
does not satisfy
$\mathcal {F}$
does not satisfy
![]() $\mathbb {C}_{suc}$
. Then there are pairs
$\mathbb {C}_{suc}$
. Then there are pairs
![]() $(m,h)$
and
$(m,h)$
and
![]() $(m,h')$
in
$(m,h')$
in
![]() $H_m$
, and
$H_m$
, and
![]() $X\subseteq MH(Tree)$
such that
$X\subseteq MH(Tree)$
such that
![]() $(m,h)R_{\mathbb {I}_a X} (m,h')$
and
$(m,h)R_{\mathbb {I}_a X} (m,h')$
and
![]() $(m,h')\notin m_a(X)$
. We choose a valuation
$(m,h')\notin m_a(X)$
. We choose a valuation
![]() $v$
such that
$v$
such that
![]() $X=\Vert p\Vert $
. We show that
$X=\Vert p\Vert $
. We show that
![]() $(m,h)R_{\Vert I_a p\Vert }(m,h')$
and
$(m,h)R_{\Vert I_a p\Vert }(m,h')$
and
![]() $\mathcal {M}, (m,h')\nvDash \square _a p$
. Since
$\mathcal {M}, (m,h')\nvDash \square _a p$
. Since
![]() $(m,h)R_{\mathbb {I}_a X} (m,h')$
and
$(m,h)R_{\mathbb {I}_a X} (m,h')$
and
![]() $(m,h')\notin m_a(X)$
, by Lemma 5.21,
$(m,h')\notin m_a(X)$
, by Lemma 5.21,
![]() $(m,h)R_{\Vert I_a p\Vert }(m,h')$
and
$(m,h)R_{\Vert I_a p\Vert }(m,h')$
and
![]() $(m,h')\notin \Vert \square p\Vert $
, respectively. So, from the latter, by definition of truth-sets,
$(m,h')\notin \Vert \square p\Vert $
, respectively. So, from the latter, by definition of truth-sets,
![]() $\mathcal {M}, (m,h)\nvDash \square _a p$
. Thus,
$\mathcal {M}, (m,h)\nvDash \square _a p$
. Thus,
![]() $\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! p$
. In Figure A.1 is a graphical representation of the (relevant part of the) countermodel used in the proof.
$\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! p$
. In Figure A.1 is a graphical representation of the (relevant part of the) countermodel used in the proof.
For better readability of the conditions, from here on, we write the conditions as open formulas, although, strictly speaking, the conditions are the universal closures of the ones we formulate here.
Simplification
Proposition 5.23.
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
and
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
and
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! C)$
iff
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! C)$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{sim}$
:
$\mathbb {C}_{sim}$
:
 $$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y\cap Z)) \Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a (Y) \text{ and } (m,h')\in m_a (Z))]. \end{align*} $$
$$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y\cap Z)) \Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a (Y) \text{ and } (m,h')\in m_a (Z))]. \end{align*} $$
Proof. Suppose
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{sim}$
. Let
$\mathbb {C}_{sim}$
. Let
![]() $\mathcal {M}$
be based on
$\mathcal {M}$
be based on
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $(m,h)$
be arbitrary. Suppose
$(m,h)$
be arbitrary. Suppose
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! (B\wedge C)$
. This entails
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! (B\wedge C)$
. This entails
![]() $\forall (m,h')((m,h)R_{\Vert I_a A\Vert }(m,h') \Rightarrow (m,h')\in (\Vert \square _a (B\wedge C)\Vert ))$
and
$\forall (m,h')((m,h)R_{\Vert I_a A\Vert }(m,h') \Rightarrow (m,h')\in (\Vert \square _a (B\wedge C)\Vert ))$
and
![]() $c(B \wedge C)\sqsubseteq c(A)$
. By Lemma 5.21, the former entails
$c(B \wedge C)\sqsubseteq c(A)$
. By Lemma 5.21, the former entails
![]() $\forall (m,h')((m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h') \Rightarrow (m,h')\in m_a(\Vert B\wedge C\Vert ))$
. Thus, the antecedent of
$\forall (m,h')((m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h') \Rightarrow (m,h')\in m_a(\Vert B\wedge C\Vert ))$
. Thus, the antecedent of
![]() $\mathbb {C}_{sim}$
for the main implication holds. We need to show that
$\mathbb {C}_{sim}$
for the main implication holds. We need to show that
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! B$
. This holds just in case for every
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! B$
. This holds just in case for every
![]() $(m,h')$
such that
$(m,h')$
such that
 $(m,h)R_{\Vert I_a (A)\Vert }(m,h')$
,
$(m,h)R_{\Vert I_a (A)\Vert }(m,h')$
,
![]() $\mathcal {M},(m,h')\vDash \square _a B$
and
$\mathcal {M},(m,h')\vDash \square _a B$
and
![]() ${c(B)\sqsubseteq c(A)}$
. Consider
${c(B)\sqsubseteq c(A)}$
. Consider
![]() $(m,h')$
s.t.
$(m,h')$
s.t.
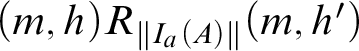 $(m,h)R_{\Vert I_a (A)\Vert }(m,h')$
. By instantiating the latter implication in
$(m,h)R_{\Vert I_a (A)\Vert }(m,h')$
. By instantiating the latter implication in
![]() $\mathbb {C}_{sim}$
, it follows that
$\mathbb {C}_{sim}$
, it follows that
![]() $(m,h')\in m_a(\Vert B\Vert )$
, and by Lemma 5.21 that
$(m,h')\in m_a(\Vert B\Vert )$
, and by Lemma 5.21 that
![]() $(m,h')\in \Vert \square _a B\Vert $
. By definition of truth-sets,
$(m,h')\in \Vert \square _a B\Vert $
. By definition of truth-sets,
![]() $\mathcal {M}, (m,h')\vDash \square _a B$
. Moreover,
$\mathcal {M}, (m,h')\vDash \square _a B$
. Moreover,
![]() $c(B)\sqsubseteq c(B)\oplus c(C)\sqsubseteq c(A)$
. So,
$c(B)\sqsubseteq c(B)\oplus c(C)\sqsubseteq c(A)$
. So,
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! B$
, and hence
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! B$
, and hence
![]() $\mathcal {M}, (m,h)\vDash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
. Similarly for C.
$\mathcal {M}, (m,h)\vDash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
. Similarly for C.
Suppose
![]() $\mathcal {F}$
does not satisfy
$\mathcal {F}$
does not satisfy
![]() $\mathbb {C}_{sim}$
. Then there are X, Y, Z, and
$\mathbb {C}_{sim}$
. Then there are X, Y, Z, and
![]() $(m,h)$
such that (i)
$(m,h)$
such that (i)
![]() $\forall (m,h')((m,h)R_{\mathbb {I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y\cap Z))$
. Moreover, (ii) there is
$\forall (m,h')((m,h)R_{\mathbb {I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y\cap Z))$
. Moreover, (ii) there is
![]() $(m,h')$
s.t.
$(m,h')$
s.t.
![]() $(m,h)R_{\mathbb {I}_a X}(m,h')$
, and (iii) not
$(m,h)R_{\mathbb {I}_a X}(m,h')$
, and (iii) not
![]() $((m,h')\in m_a (Y)$
and
$((m,h')\in m_a (Y)$
and
![]() $(m,h')\in m_a (Z) )$
. Without loss of generality, assume that
$(m,h')\in m_a (Z) )$
. Without loss of generality, assume that
![]() $(m,h')\not \in m_a(Y)$
.
$(m,h')\not \in m_a(Y)$
.

Fig. A.1 Countermodel success.
We choose a valuation
![]() $v$
such that
$v$
such that
![]() $X=\Vert p\Vert , Y=\Vert q\Vert , Z=\Vert r\Vert $
. We choose a content assignment c such that
$X=\Vert p\Vert , Y=\Vert q\Vert , Z=\Vert r\Vert $
. We choose a content assignment c such that
![]() $c(q)\sqsubseteq c(p)$
and
$c(q)\sqsubseteq c(p)$
and
![]() $c(r)\sqsubseteq c(p)$
. We show that
$c(r)\sqsubseteq c(p)$
. We show that
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! (q\wedge r)$
and
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! (q\wedge r)$
and
![]() $\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! q$
(the case for
$\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! q$
(the case for
![]() $\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! r$
is analogous). By (i) and Lemma 5.21, it follows that
$\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! r$
is analogous). By (i) and Lemma 5.21, it follows that
![]() $\forall (m,h')((m,h)R_{\Vert I_a p\Vert }(m,h') \Rightarrow (m,h')\in \Vert \square _a(q\wedge r)\Vert )$
. So, by definition of truth-sets,
$\forall (m,h')((m,h)R_{\Vert I_a p\Vert }(m,h') \Rightarrow (m,h')\in \Vert \square _a(q\wedge r)\Vert )$
. So, by definition of truth-sets,
Since
![]() $c(q)\sqsubseteq c(p)$
and
$c(q)\sqsubseteq c(p)$
and
![]() $c(r)\sqsubseteq c(p)$
, it follows by standard results that
$c(r)\sqsubseteq c(p)$
, it follows by standard results that
![]() $c(q)\oplus c(r)\sqsubseteq c(p)$
. Thus,
$c(q)\oplus c(r)\sqsubseteq c(p)$
. Thus,
![]() $c(\square _a (q\wedge r))= c(q)\oplus c(r)\sqsubseteq c(p)$
. Hence,
$c(\square _a (q\wedge r))= c(q)\oplus c(r)\sqsubseteq c(p)$
. Hence,
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! (q\wedge r)$
. By (ii) and Lemma 5.21, there is
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! (q\wedge r)$
. By (ii) and Lemma 5.21, there is
![]() $(m,h')$
such that
$(m,h')$
such that
![]() $(m,h)R_{\Vert I_a p\Vert }(m,h')$
. By our assumption about (iii), and the lemma, not
$(m,h)R_{\Vert I_a p\Vert }(m,h')$
. By our assumption about (iii), and the lemma, not
![]() $(m,h')\in \Vert \square _a q\Vert $
. So, by definition of truth-sets
$(m,h')\in \Vert \square _a q\Vert $
. So, by definition of truth-sets
![]() $\mathcal {M}, (m,h')\nvDash \square _a q$
. Therefore,
$\mathcal {M}, (m,h')\nvDash \square _a q$
. Therefore,
![]() $\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! q$
.
$\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! q$
.
Adjunction
Proposition 5.24.
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! B)\supset ((A[a]\!\!\!\rightarrow \! C)\supset (A[a]\!\!\!\rightarrow \! (B\wedge C)))$
iff
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! B)\supset ((A[a]\!\!\!\rightarrow \! C)\supset (A[a]\!\!\!\rightarrow \! (B\wedge C)))$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{adj}$
:
$\mathbb {C}_{adj}$
:
 $$ \begin{align*}&\forall (m,h)[\forall(m,h')((m,h)R_{\mathbb{I}_a X} (m,h') \Rightarrow ((m,h')\in m_a (Y) \text{ and } (m,h')\in m_a (Z))) \Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X} (m,h') \Rightarrow (m,h')\in m_a (Y\cap Z))].\end{align*} $$
$$ \begin{align*}&\forall (m,h)[\forall(m,h')((m,h)R_{\mathbb{I}_a X} (m,h') \Rightarrow ((m,h')\in m_a (Y) \text{ and } (m,h')\in m_a (Z))) \Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X} (m,h') \Rightarrow (m,h')\in m_a (Y\cap Z))].\end{align*} $$
Proof. Suppose
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{adj}$
. Let
$\mathbb {C}_{adj}$
. Let
![]() $\mathcal {M}$
be based on
$\mathcal {M}$
be based on
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $(m,h) \in MH(Tree)$
, such that
$(m,h) \in MH(Tree)$
, such that
![]() $\mathcal {M}, (m,h)\vDash A [a]\!\!\!\rightarrow \! B$
and
$\mathcal {M}, (m,h)\vDash A [a]\!\!\!\rightarrow \! B$
and
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
. By the truth-condition, this implies
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
. By the truth-condition, this implies
![]() $\forall (m,h')((m,h)R_{\Vert I_a A\Vert } (m,h') \Rightarrow ((m,h')\in \Vert \square _a B \Vert \text { and } (m,h')\in \Vert \square _a C\Vert )))$
and
$\forall (m,h')((m,h)R_{\Vert I_a A\Vert } (m,h') \Rightarrow ((m,h')\in \Vert \square _a B \Vert \text { and } (m,h')\in \Vert \square _a C\Vert )))$
and
![]() $c(B)\sqsubseteq c(A)$
and
$c(B)\sqsubseteq c(A)$
and
![]() $c(C)\sqsubseteq c(A)$
. By Lemma 5.21, it follows that
$c(C)\sqsubseteq c(A)$
. By Lemma 5.21, it follows that
So,
![]() $\forall (m,h')((m,h)R_{\mathbb {I}_a \Vert A\Vert } (m,h') \Rightarrow (m,h')\in m_a (\Vert B \wedge C\Vert ))$
. By Lemma 5.21 this is equivalent to
$\forall (m,h')((m,h)R_{\mathbb {I}_a \Vert A\Vert } (m,h') \Rightarrow (m,h')\in m_a (\Vert B \wedge C\Vert ))$
. By Lemma 5.21 this is equivalent to
We show that
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! (B\wedge C)$
. Let
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! (B\wedge C)$
. Let
![]() $(m,h')\in MH(Tree)$
be arbitrary such that
$(m,h')\in MH(Tree)$
be arbitrary such that
![]() $(m,h)R_{\Vert I_a A\Vert }(m,h')$
. By (*),
$(m,h)R_{\Vert I_a A\Vert }(m,h')$
. By (*),
![]() $(m,h')\in \square _a\Vert B\wedge C\Vert $
. So, by definition of truth-sets,
$(m,h')\in \square _a\Vert B\wedge C\Vert $
. So, by definition of truth-sets,
![]() $\mathcal {M}, (m,h')\vDash \square _a (B\wedge C)$
. Since
$\mathcal {M}, (m,h')\vDash \square _a (B\wedge C)$
. Since
![]() $c(B)\sqsubseteq c(A)$
and
$c(B)\sqsubseteq c(A)$
and
![]() $c(C)\sqsubseteq c(A)$
and
$c(C)\sqsubseteq c(A)$
and
![]() $c(B\wedge C)=c(B)\oplus c(C)$
, it follows that
$c(B\wedge C)=c(B)\oplus c(C)$
, it follows that
![]() $c(B\wedge C)\sqsubseteq c(A)$
. Since
$c(B\wedge C)\sqsubseteq c(A)$
. Since
![]() $(m,h')$
was an arbitrary pair such that
$(m,h')$
was an arbitrary pair such that
![]() $(m,h)R_{\Vert I_a A\Vert }(m,h')$
, it follows that
$(m,h)R_{\Vert I_a A\Vert }(m,h')$
, it follows that
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! (B\wedge C)$
.
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! (B\wedge C)$
.
Suppose
![]() $\mathcal {F}$
does not satisfy
$\mathcal {F}$
does not satisfy
![]() $\mathbb {C}_{adj}$
. Then there are
$\mathbb {C}_{adj}$
. Then there are
![]() $X,Y,Z$
, and
$X,Y,Z$
, and
![]() $(m,h),(m,h')$
such that
$(m,h),(m,h')$
such that
-
1.
 $\forall (m,h')((m,h)R_{\mathbb {I}_a X} (m,h') \Rightarrow ((m,h')\in m_a (Y) \text { and } (m,h')\in m_a (Z))).$
$\forall (m,h')((m,h)R_{\mathbb {I}_a X} (m,h') \Rightarrow ((m,h')\in m_a (Y) \text { and } (m,h')\in m_a (Z))).$
-
2.
 $(m,h)R_{\mathbb {I}_a X} (m,h').$
$(m,h)R_{\mathbb {I}_a X} (m,h').$
-
3.
 $(m,h')\not \in m_a (Y\cap Z).$
$(m,h')\not \in m_a (Y\cap Z).$
We choose a valuation
![]() $v$
such that
$v$
such that
![]() $X=\Vert p\Vert , Y=\Vert q\Vert , Z=\Vert r\Vert $
. We choose a content assignment c such that
$X=\Vert p\Vert , Y=\Vert q\Vert , Z=\Vert r\Vert $
. We choose a content assignment c such that
![]() $c(q)\sqsubseteq c(p)$
and
$c(q)\sqsubseteq c(p)$
and
![]() $c(r)\sqsubseteq c(p)$
.
$c(r)\sqsubseteq c(p)$
.
As for the former, it is easy to see that
![]() $\mathcal {M},(m,h)\vDash (p[a]\!\!\!\rightarrow \! q)\wedge (p[a]\!\!\!\rightarrow \! r)$
due to the content conditions and by applying Lemma 5.21 to item 1. Applying Lemma 5.21 to item 2, establishes that
$\mathcal {M},(m,h)\vDash (p[a]\!\!\!\rightarrow \! q)\wedge (p[a]\!\!\!\rightarrow \! r)$
due to the content conditions and by applying Lemma 5.21 to item 1. Applying Lemma 5.21 to item 2, establishes that
![]() $(m,h)R_{\Vert I_a p\Vert }(m,h')$
. Additionally, by Lemma 5.21, item 3 and applying the truth-condition, it follows that
$(m,h)R_{\Vert I_a p\Vert }(m,h')$
. Additionally, by Lemma 5.21, item 3 and applying the truth-condition, it follows that
![]() $\mathcal {M}, (m,h')\nvDash \square _a (q\wedge r)$
. Thus,
$\mathcal {M}, (m,h')\nvDash \square _a (q\wedge r)$
. Thus,
![]() $\mathcal {M},(m,h)\nvDash p[a]\!\!\!\rightarrow \! (q\wedge r)$
.
$\mathcal {M},(m,h)\nvDash p[a]\!\!\!\rightarrow \! (q\wedge r)$
.
Since we are modelling imaginative episodes as non-monotonic, it is worth considering some of the popular principles in the debate on non-monotonic reasoning [Reference Straßer, Antonelli and Zalta59]. Besides ST, whose analogue is Cautious Cut (see below), there is also the principle of Cautious Monotonicity.
Cautious Monotonicity
Proposition 5.25. Let
![]() $\mathcal {F}$
be a frame.
$\mathcal {F}$
be a frame.
![]() $\mathcal {F} \Vdash ((A[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset ((A\wedge B)[a]\!\!\!\rightarrow \! C)$
iff
$\mathcal {F} \Vdash ((A[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset ((A\wedge B)[a]\!\!\!\rightarrow \! C)$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{cm}$
$\mathbb {C}_{cm}$
 $$ \begin{align*}&\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow ((m,h')\in m_a (Y) \text{ and } (m,h')\in m_a(Z)))\Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a (X\cap Y)} (m,h')\Rightarrow (m,h')\in m_a(Z))]. \end{align*} $$
$$ \begin{align*}&\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow ((m,h')\in m_a (Y) \text{ and } (m,h')\in m_a(Z)))\Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a (X\cap Y)} (m,h')\Rightarrow (m,h')\in m_a(Z))]. \end{align*} $$
Proof. Let
![]() $\mathcal {F}$
be a frame satisfying
$\mathcal {F}$
be a frame satisfying
![]() $\mathbb {C}_{cm}$
,
$\mathbb {C}_{cm}$
,
![]() $\mathcal {M}$
be based on
$\mathcal {M}$
be based on
![]() $\mathcal {F}$
, and
$\mathcal {F}$
, and
![]() $(m,h)\in \mathcal {M}$
such that
$(m,h)\in \mathcal {M}$
such that
![]() $\mathcal {M} , (m,h) \vDash (A[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B)$
. From this and Lemma 5.21, it follows that for all
$\mathcal {M} , (m,h) \vDash (A[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B)$
. From this and Lemma 5.21, it follows that for all
![]() $(m,h')$
, if
$(m,h')$
, if
![]() $(m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h')$
, then
$(m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h')$
, then
![]() $(m,h')\in m_a(\Vert B\Vert )$
and
$(m,h')\in m_a(\Vert B\Vert )$
and
![]() $(m,h')\in m_a(\Vert C\Vert )$
. Suppose
$(m,h')\in m_a(\Vert C\Vert )$
. Suppose
![]() $(m,h')$
is such that
$(m,h')$
is such that
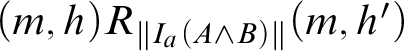 $(m,h)R_{\Vert I_a(A\wedge B)\Vert }(m,h')$
. Then by Lemma 5.21
$(m,h)R_{\Vert I_a(A\wedge B)\Vert }(m,h')$
. Then by Lemma 5.21
![]() $(m,h)R_{\mathbb {I}_a \Vert A\wedge B\Vert }(m,h')$
. By definition,
$(m,h)R_{\mathbb {I}_a \Vert A\wedge B\Vert }(m,h')$
. By definition,
 $(m,h)R_{\mathbb {I}_a (\Vert A\Vert \cap \Vert B\Vert )}(m,h')$
. Hence by
$(m,h)R_{\mathbb {I}_a (\Vert A\Vert \cap \Vert B\Vert )}(m,h')$
. Hence by
![]() $\mathbb {C}_{cm}$
,
$\mathbb {C}_{cm}$
,
![]() $(m,h')\in m_a (\Vert C\Vert )$
. By Lemma 5.21,
$(m,h')\in m_a (\Vert C\Vert )$
. By Lemma 5.21,
![]() $(m,h')\in \Vert \square _a C\Vert $
. By definition of truth-sets,
$(m,h')\in \Vert \square _a C\Vert $
. By definition of truth-sets,
![]() $\mathcal {M}, (m,h')\vDash \square _a C$
. Since
$\mathcal {M}, (m,h')\vDash \square _a C$
. Since
![]() $c(C)\sqsubseteq c(A)$
and
$c(C)\sqsubseteq c(A)$
and
![]() $c(A\wedge B)=c(A)\oplus c(B)$
, it follows that
$c(A\wedge B)=c(A)\oplus c(B)$
, it follows that
![]() $c(C)\sqsubseteq c(A\wedge B)$
. Thus,
$c(C)\sqsubseteq c(A\wedge B)$
. Thus,
![]() $\mathcal {M}, (m,h)\vDash (A\wedge B)[a]\!\!\!\rightarrow \! C$
. So
$\mathcal {M}, (m,h)\vDash (A\wedge B)[a]\!\!\!\rightarrow \! C$
. So
![]() $\mathcal {M}, (m,h')\vDash \square _a C$
.
$\mathcal {M}, (m,h')\vDash \square _a C$
.
Suppose
![]() $\mathcal {F}$
doesn’t satisfy
$\mathcal {F}$
doesn’t satisfy
![]() $\mathbb {C}_{cm}$
, then there are pairs
$\mathbb {C}_{cm}$
, then there are pairs
![]() $(m,h), (m,h')$
and sets
$(m,h), (m,h')$
and sets
![]() $Y, X$
such that
$Y, X$
such that
-
1.
 $\forall (m,h')((m,h)R_{\mathbb {I}_a X}(m,h')\Rightarrow ((m,h')\in m_a(Y)\ \&\ (m,h')\in m_a(Z))).$
$\forall (m,h')((m,h)R_{\mathbb {I}_a X}(m,h')\Rightarrow ((m,h')\in m_a(Y)\ \&\ (m,h')\in m_a(Z))).$
-
2.
 $(m,h)R_{\mathbb {I}_a (X\cap Y)}(m,h').$
$(m,h)R_{\mathbb {I}_a (X\cap Y)}(m,h').$
-
3. it is not the case that
 $(m,h')\in m_a(Z).$
$(m,h')\in m_a(Z).$
We choose c such that
![]() $c(q)\sqsubseteq c(p)$
,
$c(q)\sqsubseteq c(p)$
,
![]() $c(r)\sqsubseteq c(p)$
. We choose a valuation
$c(r)\sqsubseteq c(p)$
. We choose a valuation
![]() $v$
such that
$v$
such that
![]() $X=\Vert p\Vert $
,
$X=\Vert p\Vert $
,
![]() $Y=\Vert q\Vert $
,
$Y=\Vert q\Vert $
,
![]() $Z=\Vert r\Vert $
. By 1 and 3, we know that it is not the case that
$Z=\Vert r\Vert $
. By 1 and 3, we know that it is not the case that
![]() $(m,h)R_{\mathbb {I}_a\Vert p\Vert }(m,h')$
. We show that
$(m,h)R_{\mathbb {I}_a\Vert p\Vert }(m,h')$
. We show that
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
and
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
and
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! r$
but
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! r$
but
![]() $\mathcal {M}, (m,h)\nvDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
. The former two we obtain by applying Lemma 5.21 to item 1. By Lemma 5.21, item 2, and definition of truth-sets, we get that
$\mathcal {M}, (m,h)\nvDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
. The former two we obtain by applying Lemma 5.21 to item 1. By Lemma 5.21, item 2, and definition of truth-sets, we get that
 $(m,h)R_{\Vert I_a (p \wedge q)\Vert )}(m,h')$
. By Lemma 5.21 and item 3, it follows that
$(m,h)R_{\Vert I_a (p \wedge q)\Vert )}(m,h')$
. By Lemma 5.21 and item 3, it follows that
![]() $\mathcal {M},(m,h')\nvDash \square _a r$
. Hence
$\mathcal {M},(m,h')\nvDash \square _a r$
. Hence
![]() $\mathcal {M}, (m,h)\nvDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
. For the graphical countermodel see (Figure A.2).
$\mathcal {M}, (m,h)\nvDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
. For the graphical countermodel see (Figure A.2).
Cautious Cut
Proposition 5.26.
![]() $\mathcal {F}\Vdash (((A\wedge B) [a]\!\!\!\rightarrow \! C) \wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
iff
$\mathcal {F}\Vdash (((A\wedge B) [a]\!\!\!\rightarrow \! C) \wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{cc}$
:
$\mathbb {C}_{cc}$
:
 $$ \begin{align*}&\forall (m,h)[(\forall(m,h')((m,h)R_{\mathbb{I}_a(X\cap Y)} (m,h')\Rightarrow (m,h')\in m_a (Z))\ \&\ \\ &\forall(m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y)))\Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X} (m,h')\Rightarrow (m,h')\in m_a(Z))]. \end{align*} $$
$$ \begin{align*}&\forall (m,h)[(\forall(m,h')((m,h)R_{\mathbb{I}_a(X\cap Y)} (m,h')\Rightarrow (m,h')\in m_a (Z))\ \&\ \\ &\forall(m,h')((m,h)R_{\mathbb{I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y)))\Rightarrow \\ &\forall (m,h')((m,h)R_{\mathbb{I}_a X} (m,h')\Rightarrow (m,h')\in m_a(Z))]. \end{align*} $$
Proof. Let
![]() $\mathcal {F}$
be a stit-imagination episode frame satisfying
$\mathcal {F}$
be a stit-imagination episode frame satisfying
![]() $\mathbb {C}_{cc}$
. Let
$\mathbb {C}_{cc}$
. Let
![]() $\mathcal {M}$
be based on
$\mathcal {M}$
be based on
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $(m,h)\in \mathcal {M}$
be such that
$(m,h)\in \mathcal {M}$
be such that
![]() $\mathcal {M} ,(m,h)\vDash ((A\wedge B) [a]\!\!\!\rightarrow \! C) \wedge (A[a]\!\!\!\rightarrow \! B)$
. By the first conjunct, Lemma 5.21, and the definition of truth-sets, we know that
$\mathcal {M} ,(m,h)\vDash ((A\wedge B) [a]\!\!\!\rightarrow \! C) \wedge (A[a]\!\!\!\rightarrow \! B)$
. By the first conjunct, Lemma 5.21, and the definition of truth-sets, we know that
 $\forall (m,h')((m,h)R_{\mathbb {I}_a(\Vert A\Vert \cap \Vert B\Vert )}(m,h')\Rightarrow (m,h')\in m_a(\Vert C\Vert ))$
. By Lemma 5.21 and
$\forall (m,h')((m,h)R_{\mathbb {I}_a(\Vert A\Vert \cap \Vert B\Vert )}(m,h')\Rightarrow (m,h')\in m_a(\Vert C\Vert ))$
. By Lemma 5.21 and
![]() $\mathcal {M} ,(m,h)\vDash A [a]\!\!\!\rightarrow \! B$
, we know that for all
$\mathcal {M} ,(m,h)\vDash A [a]\!\!\!\rightarrow \! B$
, we know that for all
![]() $(m,h')$
,
$(m,h')$
,
![]() $(m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h') \Rightarrow (m,h')\in m_a(\Vert B\Vert )$
.
$(m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h') \Rightarrow (m,h')\in m_a(\Vert B\Vert )$
.

Fig. A.2 Countermodel cautious monotonicity.
We want to show that
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
. Suppose
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
. Suppose
![]() $(m,h')$
is such that
$(m,h')$
is such that
![]() $(m,h)R_{\mathbb {I}_a \Vert A\Vert } (m,h')$
. By
$(m,h)R_{\mathbb {I}_a \Vert A\Vert } (m,h')$
. By
![]() $\mathbb {C}_{cc}$
,
$\mathbb {C}_{cc}$
,
![]() $(m,h')\in m_a(\Vert C\Vert )$
, which by Lemma 5.21 and the definition of truth-sets entails that
$(m,h')\in m_a(\Vert C\Vert )$
, which by Lemma 5.21 and the definition of truth-sets entails that
![]() $\mathcal {M}, (m,h')\vDash \square _a C$
. Since
$\mathcal {M}, (m,h')\vDash \square _a C$
. Since
![]() $c(C)\sqsubseteq c(A\wedge B)=c(A)\oplus c(B)$
and
$c(C)\sqsubseteq c(A\wedge B)=c(A)\oplus c(B)$
and
![]() $c(B)\sqsubseteq c(A)$
, it follows that
$c(B)\sqsubseteq c(A)$
, it follows that
![]() $c(C)\sqsubseteq c(A)$
. Since
$c(C)\sqsubseteq c(A)$
. Since
![]() $(m,h')$
was arbitrary, we conclude
$(m,h')$
was arbitrary, we conclude
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
.
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
.
Let
![]() $\mathcal {F}$
be a frame not satisfying
$\mathcal {F}$
be a frame not satisfying
![]() $\mathbb {C}_{cc}$
. Then there are
$\mathbb {C}_{cc}$
. Then there are
![]() $(m,h), (m,h')$
and sets X, Y, Z such that
$(m,h), (m,h')$
and sets X, Y, Z such that
-
1.
 $\forall (m,h')((m,h)R_{\mathbb {I}_a (X\cap Y)}(m,h') \Rightarrow (m,h')\in m_a(Z)).$
$\forall (m,h')((m,h)R_{\mathbb {I}_a (X\cap Y)}(m,h') \Rightarrow (m,h')\in m_a(Z)).$
-
2.
 $\forall (m,h')((m,h)R_{\mathbb {I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y)).$
$\forall (m,h')((m,h)R_{\mathbb {I}_a X}(m,h') \Rightarrow (m,h')\in m_a(Y)).$
-
3.
 $(m,h)R_{\mathbb {I}_a X} (m,h').$
$(m,h)R_{\mathbb {I}_a X} (m,h').$
-
4. not
 $(m,h')\in m_a(Z)$
.
$(m,h')\in m_a(Z)$
.
We choose a valuation
![]() $v$
such that
$v$
such that
![]() $X=\Vert p\Vert $
,
$X=\Vert p\Vert $
,
![]() $Y=\Vert q\Vert $
,
$Y=\Vert q\Vert $
,
![]() $Z=\Vert r\Vert $
. We choose c such that
$Z=\Vert r\Vert $
. We choose c such that
![]() $c(r)\sqsubseteq c(p)$
and
$c(r)\sqsubseteq c(p)$
and
![]() $c(q)\sqsubseteq c(p)$
.
$c(q)\sqsubseteq c(p)$
.

Fig. A.3 Countermodel cautious cut.
We now show that
![]() $\mathcal {M}, (m,h)\nvDash ((p[a]\!\!\!\rightarrow \! q) \wedge (p\wedge q)[a]\!\!\!\rightarrow \! r)\supset (p[a]\!\!\!\rightarrow \! r)$
. By item 1 and Lemma 5.21, it holds that
$\mathcal {M}, (m,h)\nvDash ((p[a]\!\!\!\rightarrow \! q) \wedge (p\wedge q)[a]\!\!\!\rightarrow \! r)\supset (p[a]\!\!\!\rightarrow \! r)$
. By item 1 and Lemma 5.21, it holds that
![]() $\mathcal {M}, (m,h)\vDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
. By item 2 and Lemma 5.21, it holds that
$\mathcal {M}, (m,h)\vDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
. By item 2 and Lemma 5.21, it holds that
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
. By item 4 and Lemma 5.21, it follows that
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
. By item 4 and Lemma 5.21, it follows that
![]() $\mathcal {M}, (m,h')\nvDash \square _a r$
. By item 3 and Lemma 5.21,
$\mathcal {M}, (m,h')\nvDash \square _a r$
. By item 3 and Lemma 5.21,
![]() $\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! r$
. For the graphical countermodel (again, omitting content assignments), see Figure A.3.
$\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! r$
. For the graphical countermodel (again, omitting content assignments), see Figure A.3.
Substitutivity
Recall
Definition 5.27. Given a frame
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $X\subseteq MH(Tree)$
, we define
$X\subseteq MH(Tree)$
, we define
![]() $f(X, (m,h))=\lbrace (m, h') \in MH(Tree) | (m,h)R_X (m, h'))\rbrace $
.
$f(X, (m,h))=\lbrace (m, h') \in MH(Tree) | (m,h)R_X (m, h'))\rbrace $
.
Proposition 5.28.
![]() $\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! B)\wedge (B [a]\!\!\!\rightarrow \! A) \wedge (A[a]\!\!\!\rightarrow \! C) ) \supset B[a]\!\!\!\rightarrow \! C$
iff
$\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! B)\wedge (B [a]\!\!\!\rightarrow \! A) \wedge (A[a]\!\!\!\rightarrow \! C) ) \supset B[a]\!\!\!\rightarrow \! C$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{pie}$
:
$\mathbb {C}_{pie}$
:
 $$ \begin{align*}&(f(\mathbb{I}_a X, (m,h)) \subseteq m_a(Y)\ \&\ f(\mathbb{I}_a Y, (m,h)) \subseteq m_a(X)\ \&\ f(\mathbb{I}_a X, (m,h)) \subseteq m_a(Z)) \Rightarrow\\ &f(\mathbb{I}_a Y, (m,h)) \subseteq m_a(Z).\end{align*} $$
$$ \begin{align*}&(f(\mathbb{I}_a X, (m,h)) \subseteq m_a(Y)\ \&\ f(\mathbb{I}_a Y, (m,h)) \subseteq m_a(X)\ \&\ f(\mathbb{I}_a X, (m,h)) \subseteq m_a(Z)) \Rightarrow\\ &f(\mathbb{I}_a Y, (m,h)) \subseteq m_a(Z).\end{align*} $$
Proof. Suppose
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{pie}$
. Let
$\mathbb {C}_{pie}$
. Let
![]() $\mathcal {M}$
be based on
$\mathcal {M}$
be based on
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
-
1.
 $M, (m,h)\vDash (A[a]\!\!\!\rightarrow \! C)$
iff
$M, (m,h)\vDash (A[a]\!\!\!\rightarrow \! C)$
iff
 $\ \forall \ h'\in H_m( (m,h)R_{\Vert I_a A\Vert }(m,h') \Rightarrow \Vert C\Vert \in N_a((m,h')) )$
and
$\ \forall \ h'\in H_m( (m,h)R_{\Vert I_a A\Vert }(m,h') \Rightarrow \Vert C\Vert \in N_a((m,h')) )$
and
 $c(C)\sqsubseteq c(A)$
$c(C)\sqsubseteq c(A)$
-
2.
 $M, (m,h)\vDash (A[a]\!\!\!\rightarrow \! B)$
iff
$M, (m,h)\vDash (A[a]\!\!\!\rightarrow \! B)$
iff
 $\ \forall \ h'\in H_m( (m,h)R_{\Vert I_a A\Vert }(m,h') \Rightarrow \Vert B\Vert \in N_a((m,h')) )$
and
$\ \forall \ h'\in H_m( (m,h)R_{\Vert I_a A\Vert }(m,h') \Rightarrow \Vert B\Vert \in N_a((m,h')) )$
and
 $c(B)\sqsubseteq c(A)$
$c(B)\sqsubseteq c(A)$
-
3.
 $M, (m,h)\vDash (B[a]\!\!\!\rightarrow \! A)$
iff
$M, (m,h)\vDash (B[a]\!\!\!\rightarrow \! A)$
iff
 $\ \forall \ h'\in H_m( (m,h)R_{\Vert I_a B\Vert }(m,h') \Rightarrow \Vert A\Vert \in N_a((m,h')) )$
and
$\ \forall \ h'\in H_m( (m,h)R_{\Vert I_a B\Vert }(m,h') \Rightarrow \Vert A\Vert \in N_a((m,h')) )$
and
 $c(A)\sqsubseteq c(B)$
$c(A)\sqsubseteq c(B)$
Hence,
![]() $c(C)\sqsubseteq c(B)$
.
$c(C)\sqsubseteq c(B)$
.
By items 1–3 and Lemma 5.21, we have it that
![]() $f(\mathbb {I}_a\Vert A\Vert , (m,h)) \subseteq m_a(\Vert B\Vert )$
and
$f(\mathbb {I}_a\Vert A\Vert , (m,h)) \subseteq m_a(\Vert B\Vert )$
and
![]() $ f(\mathbb {I}_a\Vert B\Vert , (m,h)) \subseteq m_a(\Vert A\Vert )$
and
$ f(\mathbb {I}_a\Vert B\Vert , (m,h)) \subseteq m_a(\Vert A\Vert )$
and
![]() $ f(\mathbb {I}_a\Vert A\Vert , (m,h)) \subseteq m_a(\Vert C\Vert )$
. Thus, by
$ f(\mathbb {I}_a\Vert A\Vert , (m,h)) \subseteq m_a(\Vert C\Vert )$
. Thus, by
![]() $\mathbb {C}_{pie}$
,
$\mathbb {C}_{pie}$
,
![]() $f(\mathbb {I}_a\Vert B\Vert , (m,h)) \subseteq m_a(\Vert C\Vert )$
.
$f(\mathbb {I}_a\Vert B\Vert , (m,h)) \subseteq m_a(\Vert C\Vert )$
.
We show that
![]() $M, (m,h)\vDash {B[a]\!\!\!\rightarrow \!} C$
. That is,
$M, (m,h)\vDash {B[a]\!\!\!\rightarrow \!} C$
. That is,
![]() $\forall h'\in H_m( (m,h)R_{\Vert I_a B\Vert }(m,h') \Rightarrow \Vert C\Vert \in N_a((m,h')) )$
and
$\forall h'\in H_m( (m,h)R_{\Vert I_a B\Vert }(m,h') \Rightarrow \Vert C\Vert \in N_a((m,h')) )$
and
![]() $c(C)\sqsubseteq c(B)$
. The latter, we already established. Consider an
$c(C)\sqsubseteq c(B)$
. The latter, we already established. Consider an
![]() $(m,h')$
such that
$(m,h')$
such that
![]() $(m,h)R_{\Vert I_a B\Vert }(m,h') $
, i.e.,
$(m,h)R_{\Vert I_a B\Vert }(m,h') $
, i.e.,
![]() $(m,h')\in f(\mathbb {I}_a \Vert B\Vert , (m,h))$
. So,
$(m,h')\in f(\mathbb {I}_a \Vert B\Vert , (m,h))$
. So,
![]() $(m,h')\in m_a (\Vert C\Vert )$
. By Lemma 5.21 and definition of truth-sets, it follows that
$(m,h')\in m_a (\Vert C\Vert )$
. By Lemma 5.21 and definition of truth-sets, it follows that
![]() $\mathcal {M}, (m,h')\vDash \square _a C$
. Since
$\mathcal {M}, (m,h')\vDash \square _a C$
. Since
![]() $(m,h')$
was arbitrary,
$(m,h')$
was arbitrary,
![]() $\mathcal {M}, (m,h)\vDash B[a]\!\!\!\rightarrow \! C$
.
$\mathcal {M}, (m,h)\vDash B[a]\!\!\!\rightarrow \! C$
.
Suppose
![]() $\mathcal {F}$
does not satisfy
$\mathcal {F}$
does not satisfy
![]() $\mathbb {C}_{pie}$
. Then there are agent a,
$\mathbb {C}_{pie}$
. Then there are agent a,
![]() $(m,h)$
and sets
$(m,h)$
and sets
![]() $X, Y, Z$
such that
$X, Y, Z$
such that
-
1.
 $f(\mathbb {I}_a X, (m,h)) \subseteq m_a(Y).$
$f(\mathbb {I}_a X, (m,h)) \subseteq m_a(Y).$
-
2.
 $f(\mathbb {I}_a Y, (m,h)) \subseteq m_a (X).$
$f(\mathbb {I}_a Y, (m,h)) \subseteq m_a (X).$
-
3.
 $f(\mathbb {I}_a X, (m,h)) \subseteq m_a(Z). $
$f(\mathbb {I}_a X, (m,h)) \subseteq m_a(Z). $
-
4.
 $f(\mathbb {I}_a Y, (m,h)) \not \subseteq m_a(Z). $
$f(\mathbb {I}_a Y, (m,h)) \not \subseteq m_a(Z). $
By 4, there is
![]() $(m,h')\in f(\mathbb {I}_a Y, (m,h))$
and
$(m,h')\in f(\mathbb {I}_a Y, (m,h))$
and
![]() $(m,h')\not \in m_a(Z)$
. We choose a valuation
$(m,h')\not \in m_a(Z)$
. We choose a valuation
![]() $v$
such that
$v$
such that
![]() $X=\Vert p\Vert $
,
$X=\Vert p\Vert $
,
![]() $Y=\Vert q\Vert $
,
$Y=\Vert q\Vert $
,
![]() $Z=\Vert r\Vert $
. We choose a content assignment c such that
$Z=\Vert r\Vert $
. We choose a content assignment c such that
![]() $c(r)\sqsubseteq c(p)=c(q)$
. We show that
$c(r)\sqsubseteq c(p)=c(q)$
. We show that
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! r \wedge p[a]\!\!\!\rightarrow \! q \wedge q[a]\!\!\!\rightarrow \! p$
and
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! r \wedge p[a]\!\!\!\rightarrow \! q \wedge q[a]\!\!\!\rightarrow \! p$
and
![]() $\mathcal {M}, (m,h)\nvDash q[a]\!\!\!\rightarrow \! r$
. Consider a pair
$\mathcal {M}, (m,h)\nvDash q[a]\!\!\!\rightarrow \! r$
. Consider a pair
![]() $(m,h')$
such that
$(m,h')$
such that
![]() $(m,h)R_{\Vert I_a p\Vert }(m,h')$
. By Lemma 5.21,
$(m,h)R_{\Vert I_a p\Vert }(m,h')$
. By Lemma 5.21,
 $(m,h)R_{\mathbb {I}_a (\Vert p\Vert )}(m,h')$
. Then by item 1,
$(m,h)R_{\mathbb {I}_a (\Vert p\Vert )}(m,h')$
. Then by item 1,
![]() $(m,h')\in m_a(\Vert q\Vert )$
. Hence, by Lemma 5.21,
$(m,h')\in m_a(\Vert q\Vert )$
. Hence, by Lemma 5.21,
![]() $(m,h')\in \Vert \square _a q\Vert $
. By the definition of truth-sets,
$(m,h')\in \Vert \square _a q\Vert $
. By the definition of truth-sets,
![]() $\mathcal {M}, (m,h')\vDash \square _a q$
. Since
$\mathcal {M}, (m,h')\vDash \square _a q$
. Since
![]() $c(p)=c(q)$
,
$c(p)=c(q)$
,
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
. The case for
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
. The case for
![]() $\mathcal {M}, (m,h)\vDash q[a]\!\!\!\rightarrow \! p$
is analogous and utilises item 2. The case for
$\mathcal {M}, (m,h)\vDash q[a]\!\!\!\rightarrow \! p$
is analogous and utilises item 2. The case for
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! r$
is analogous and uses 3 and the fact that
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! r$
is analogous and uses 3 and the fact that
![]() $c(r)\sqsubseteq c(p)$
.
$c(r)\sqsubseteq c(p)$
.

Fig. A.4 Countermodel substitutivity.
For
![]() $\mathcal {M}, (m,h)\nvDash q[a]\!\!\!\rightarrow \! r$
, we know that there is
$\mathcal {M}, (m,h)\nvDash q[a]\!\!\!\rightarrow \! r$
, we know that there is
![]() $(m,h')\in f(\mathbb {I}_a Y, (m,h))$
and
$(m,h')\in f(\mathbb {I}_a Y, (m,h))$
and
![]() $(m,h')\not \in m_a(Z)$
. By Lemma 5.21,
$(m,h')\not \in m_a(Z)$
. By Lemma 5.21,
![]() $(m,h)R_{\Vert I_a q\Vert }(m,h')$
and
$(m,h)R_{\Vert I_a q\Vert }(m,h')$
and
![]() $(m,h')\not \in \Vert \square _a r\Vert $
. So, by definition of truth-sets,
$(m,h')\not \in \Vert \square _a r\Vert $
. So, by definition of truth-sets,
![]() $\mathcal {M}, (m,h')\nvDash \square _a r$
. Hence,
$\mathcal {M}, (m,h')\nvDash \square _a r$
. Hence,
![]() $\mathcal {M}, (m,h')\nvDash q[a]\!\!\!\rightarrow \! r$
. For the graphical countermodel (again, omitting content assignments), see Figure A.4.
$\mathcal {M}, (m,h')\nvDash q[a]\!\!\!\rightarrow \! r$
. For the graphical countermodel (again, omitting content assignments), see Figure A.4.
Closure under Imagined Implication (eCII)
Proposition 5.29.
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\supset C)) \supset ((A[a]\!\!\!\rightarrow \! B)\supset (A[a]\!\!\!\rightarrow \! C))$
iff
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\supset C)) \supset ((A[a]\!\!\!\rightarrow \! B)\supset (A[a]\!\!\!\rightarrow \! C))$
iff
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{CII}$
:
$\mathbb {C}_{CII}$
:
 $$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow ((m,h')\in m_a((MH(Tree)\setminus Y)\cup Z)\\ &\&\ (m,h')\in m_a(Y)) \Rightarrow \forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow (m,h')\in m_a(Z)))]. \end{align*} $$
$$ \begin{align*} &\forall (m,h)[\forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow ((m,h')\in m_a((MH(Tree)\setminus Y)\cup Z)\\ &\&\ (m,h')\in m_a(Y)) \Rightarrow \forall (m,h')((m,h)R_{\mathbb{I}_a X}(m,h')\Rightarrow (m,h')\in m_a(Z)))]. \end{align*} $$
Proof. Let
![]() $\mathcal {F}$
be a frame satisfying
$\mathcal {F}$
be a frame satisfying
![]() $\mathbb {C}_{CII}$
. Let
$\mathbb {C}_{CII}$
. Let
![]() $\mathcal {M}$
be a model based on
$\mathcal {M}$
be a model based on
![]() $\mathcal {F}$
with
$\mathcal {F}$
with
![]() $(m,h)$
in
$(m,h)$
in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathcal {M}, (m,h)\vDash A [a]\!\!\!\rightarrow \! (B\supset C)$
and
$\mathcal {M}, (m,h)\vDash A [a]\!\!\!\rightarrow \! (B\supset C)$
and
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! B$
. It follows that
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! B$
. It follows that
![]() $c(B\supset C)=c(B)\oplus c(C)\sqsubseteq c(A)$
. By the truth-conditions, the definition of truth-sets and Lemma 5.21, it follows that
$c(B\supset C)=c(B)\oplus c(C)\sqsubseteq c(A)$
. By the truth-conditions, the definition of truth-sets and Lemma 5.21, it follows that
 $$ \begin{align*}&\forall (m,h')((m,h)R_{\mathbb{I}_a \Vert A\Vert}(m,h')\Rightarrow ((m,h')\in m_a((MH(Tree)\setminus \Vert B\Vert)\cup \Vert C\Vert)\\ &\&\ (m,h')\in m_a(\Vert B\Vert))).\end{align*} $$
$$ \begin{align*}&\forall (m,h')((m,h)R_{\mathbb{I}_a \Vert A\Vert}(m,h')\Rightarrow ((m,h')\in m_a((MH(Tree)\setminus \Vert B\Vert)\cup \Vert C\Vert)\\ &\&\ (m,h')\in m_a(\Vert B\Vert))).\end{align*} $$
Thus,
![]() $\forall (m,h')((m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h')\Rightarrow (m,h')\in m_a(\Vert C\Vert ))$
by
$\forall (m,h')((m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h')\Rightarrow (m,h')\in m_a(\Vert C\Vert ))$
by
![]() $\mathbb {C}_{CII}$
.
$\mathbb {C}_{CII}$
.
We show that
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
. Let
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
. Let
![]() $(m,h')$
be such that
$(m,h')$
be such that
![]() $(m,h)R_{\Vert I_a A\Vert }(m,h')$
. By Lemma 5.21, we have
$(m,h)R_{\Vert I_a A\Vert }(m,h')$
. By Lemma 5.21, we have
![]() $(m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h')$
. So, by
$(m,h)R_{\mathbb {I}_a \Vert A\Vert }(m,h')$
. So, by
![]() $\mathbb {C}_{CII}$
,
$\mathbb {C}_{CII}$
,
![]() $(m,h')\in m_a (\Vert C\Vert )$
. By Lemma 5.21 and definition of truth-sets,
$(m,h')\in m_a (\Vert C\Vert )$
. By Lemma 5.21 and definition of truth-sets,
![]() $\mathcal {M},(m,h')\vDash \square _a C$
. Since
$\mathcal {M},(m,h')\vDash \square _a C$
. Since
![]() $c(B\supset C)=c(B)\oplus c(C)\sqsubseteq c(A)$
and
$c(B\supset C)=c(B)\oplus c(C)\sqsubseteq c(A)$
and
![]() $c(C)\sqsubseteq c(B)\oplus c(C)$
, we have that
$c(C)\sqsubseteq c(B)\oplus c(C)$
, we have that
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
.
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
.
Suppose
![]() $\mathcal {F}$
doesn’t satisfy
$\mathcal {F}$
doesn’t satisfy
![]() $\mathbb {C}_{CII}$
. Then there are
$\mathbb {C}_{CII}$
. Then there are
![]() $X,Y,Z$
and
$X,Y,Z$
and
![]() $(m,h)$
and
$(m,h)$
and
![]() $(m,h')$
such that
$(m,h')$
such that
-
1.
 $\forall (m,h')((m,h)R_{\mathbb {I}_a X}(m,h')\Rightarrow ((m,h')\in m_a(((MH(Tree)\setminus Y)\cup Z))\ \&(m,h') \in m_a(Y))).$
$\forall (m,h')((m,h)R_{\mathbb {I}_a X}(m,h')\Rightarrow ((m,h')\in m_a(((MH(Tree)\setminus Y)\cup Z))\ \&(m,h') \in m_a(Y))).$
-
2.
 $(m,h)R_{\mathbb {I}_a X}(m,h').$
$(m,h)R_{\mathbb {I}_a X}(m,h').$
-
3.
 $(m,h')\not \in m_a(Z).$
$(m,h')\not \in m_a(Z).$
We choose a valuation
![]() $v$
such that
$v$
such that
![]() $X=\Vert p\Vert , Y=\Vert q\Vert , Z=\Vert r\Vert $
and a content assignment c such that
$X=\Vert p\Vert , Y=\Vert q\Vert , Z=\Vert r\Vert $
and a content assignment c such that
![]() $c(q)\sqsubseteq c(p)$
and
$c(q)\sqsubseteq c(p)$
and
![]() $c(r)\sqsubseteq c(p)$
. By Lemma 5.21, definition of truth-sets, and the truth-conditions, it follows by item 1 that
$c(r)\sqsubseteq c(p)$
. By Lemma 5.21, definition of truth-sets, and the truth-conditions, it follows by item 1 that
![]() $\mathcal {M}, (m,h)\vDash (p[a]\!\!\!\rightarrow \! (q\supset r))\wedge (p[a]\!\!\!\rightarrow \! q)$
.
$\mathcal {M}, (m,h)\vDash (p[a]\!\!\!\rightarrow \! (q\supset r))\wedge (p[a]\!\!\!\rightarrow \! q)$
.

Fig. A.5 Countermodel CII.
By item 2 and Lemma 5.21,
![]() $(m,h)R_{\Vert I_a p\Vert }(m,h')$
. By item 3, Lemma 5.21 and the definition of truth-sets, it follows that
$(m,h)R_{\Vert I_a p\Vert }(m,h')$
. By item 3, Lemma 5.21 and the definition of truth-sets, it follows that
![]() $\mathcal {M}, (m,h')\nvDash \square _a r$
. Hence
$\mathcal {M}, (m,h')\nvDash \square _a r$
. Hence
![]() $\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! r$
. For the graphical countermodel, where
$\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! r$
. For the graphical countermodel, where
 $\overline {\Vert q\Vert }:= MH(Tree)\setminus \Vert q\Vert $
, and we know that
$\overline {\Vert q\Vert }:= MH(Tree)\setminus \Vert q\Vert $
, and we know that
 $\overline {\Vert q\Vert }\cup \Vert r\Vert \neq \Vert r\Vert $
see (Figure A.5).
$\overline {\Vert q\Vert }\cup \Vert r\Vert \neq \Vert r\Vert $
see (Figure A.5).
Proposition 5.30. Let
![]() $\mathcal {F}$
be a frame. It is not the case that if
$\mathcal {F}$
be a frame. It is not the case that if
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{suc}$
,
$\mathbb {C}_{suc}$
,
![]() $\mathbb {C}_{sim}$
, and
$\mathbb {C}_{sim}$
, and
![]() $\mathbb {C}_{adj}$
, then
$\mathbb {C}_{adj}$
, then
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{cc}$
.
$\mathbb {C}_{cc}$
.
Proof. It suffices to show that there is a model in which
![]() $\mathbb {C}_{suc}$
,
$\mathbb {C}_{suc}$
,
![]() $\mathbb {C}_{sim}$
, and
$\mathbb {C}_{sim}$
, and
![]() $\mathbb {C}_{adj}$
are satisfied but
$\mathbb {C}_{adj}$
are satisfied but
![]() $\mathbb {C}_{cc}$
is not.
$\mathbb {C}_{cc}$
is not.
Let
![]() $\mathcal {M}=\langle Tree, \leq , Ag, Choice, \lbrace N_a \mid a\in Ag\rbrace , R, P, \textsf {C}, \oplus , c, v\rangle $
be a model such that
$\mathcal {M}=\langle Tree, \leq , Ag, Choice, \lbrace N_a \mid a\in Ag\rbrace , R, P, \textsf {C}, \oplus , c, v\rangle $
be a model such that
-
•
 $Tree =\lbrace m, m'', m'\rbrace $
,
$Tree =\lbrace m, m'', m'\rbrace $
, -
•
 $\leq = \lbrace (m, m'), (m,m'), (m,m), (m'',m'), (m'',m') \rbrace $
,
$\leq = \lbrace (m, m'), (m,m'), (m,m), (m'',m'), (m'',m') \rbrace $
, -
•
 $h' = \{(m,m), (m,m'), (m'',m') \}$
,
$h' = \{(m,m), (m,m'), (m'',m') \}$
,
 $h' = \{(m,m), (m,m'), (m'',m') \}$
,
$h' = \{(m,m), (m,m'), (m'',m') \}$
, -
•
 $Ag=\lbrace a\rbrace $
,
$Ag=\lbrace a\rbrace $
, -
•
 $Choice_a(m, h')=\lbrace h'', h'\rbrace $
,
$Choice_a(m, h')=\lbrace h'', h'\rbrace $
,
 $Choice_a(m'', h')=\lbrace h'\rbrace $
$Choice_a(m'', h')=\lbrace h'\rbrace $
-
•
 $N_a((m,h')) = N_a((m,h'))=\varnothing $
,
$N_a((m,h')) = N_a((m,h'))=\varnothing $
,
 $N_a((m'',h'))=\lbrace \Vert p\Vert \cap \Vert q\Vert , \Vert p\Vert , \Vert q\Vert , \Vert r\Vert , \Vert p\Vert \cap \Vert r\Vert , \Vert q\Vert \cap \Vert r\Vert \rbrace $
,
$N_a((m'',h'))=\lbrace \Vert p\Vert \cap \Vert q\Vert , \Vert p\Vert , \Vert q\Vert , \Vert r\Vert , \Vert p\Vert \cap \Vert r\Vert , \Vert q\Vert \cap \Vert r\Vert \rbrace $
,
 $N_a((m'',h'))=\lbrace \Vert p\Vert , \Vert q\Vert , \Vert p\Vert \cap \Vert q\Vert \rbrace $
,
$N_a((m'',h'))=\lbrace \Vert p\Vert , \Vert q\Vert , \Vert p\Vert \cap \Vert q\Vert \rbrace $
, -
•
 $R_{\mathbb {I}_a \Vert p\Vert }=\lbrace ((m,h'),(m'',h'), ((m,h'),(m'',h'))\rbrace $
,
$R_{\mathbb {I}_a \Vert p\Vert }=\lbrace ((m,h'),(m'',h'), ((m,h'),(m'',h'))\rbrace $
,
 $R_{\mathbb {I}_a(\Vert p\Vert \cap \Vert q\Vert )}=\lbrace ((m,h'), (m'',h')),((m,h'),(m'',h')) \rbrace $
, all other relations are empty.
$R_{\mathbb {I}_a(\Vert p\Vert \cap \Vert q\Vert )}=\lbrace ((m,h'), (m'',h')),((m,h'),(m'',h')) \rbrace $
, all other relations are empty. -
•
 $P=\mathcal {P}(MH(Tree))$
,
$P=\mathcal {P}(MH(Tree))$
, -
•
 $\langle \textsf {C}, \oplus , c\rangle $
is a content model with a content assignment c such that
$\langle \textsf {C}, \oplus , c\rangle $
is a content model with a content assignment c such that
 $c(r)\sqsubseteq c(p)$
and
$c(r)\sqsubseteq c(p)$
and
 $c(q)\sqsubseteq c(p)$
.
$c(q)\sqsubseteq c(p)$
. -
•
 $v(p)=\Vert p\Vert =\lbrace (m,h'), (m'',h'), (m'', h')\rbrace $
,
$v(p)=\Vert p\Vert =\lbrace (m,h'), (m'',h'), (m'', h')\rbrace $
,
 $v(q)=\Vert q\Vert =\lbrace (m'',h')\rbrace $
,
$v(q)=\Vert q\Vert =\lbrace (m'',h')\rbrace $
,
 $v(r)=\Vert r\Vert =\lbrace (m'',h')\rbrace $
.
$v(r)=\Vert r\Vert =\lbrace (m'',h')\rbrace $
.
We first show that
![]() $\mathbb {C}_{suc}$
,
$\mathbb {C}_{suc}$
,
![]() $\mathbb {C}_{sim}$
, and
$\mathbb {C}_{sim}$
, and
![]() $\mathbb {C}_{adj}$
are satisfied.
$\mathbb {C}_{adj}$
are satisfied.
![]() $\mathbb {C}_{suc}$
is satisfied: We have to consider only the following instances: the one involving the set of evaluation indices
$\mathbb {C}_{suc}$
is satisfied: We have to consider only the following instances: the one involving the set of evaluation indices
![]() $\Vert p\Vert $
and the pairs of moment/history pairs
$\Vert p\Vert $
and the pairs of moment/history pairs
![]() $((m,h'),((m'',h'))$
and
$((m,h'),((m'',h'))$
and
![]() $((m,h'),(m'',h'))$
for these are the only pairs in
$((m,h'),(m'',h'))$
for these are the only pairs in
![]() $R_{\mathbb {I}_a \Vert p\Vert }$
; and the instance involving set
$R_{\mathbb {I}_a \Vert p\Vert }$
; and the instance involving set
![]() $\Vert p\Vert \cap \Vert q\Vert $
and the pairs of moment/history pairs
$\Vert p\Vert \cap \Vert q\Vert $
and the pairs of moment/history pairs
![]() $((m,h'),(m'',h')), $
and
$((m,h'),(m'',h')), $
and
![]() $((m,h'),(m'',h'))$
for these are the only elements in
$((m,h'),(m'',h'))$
for these are the only elements in
![]() $R_{\mathbb {I}_a(\Vert p\Vert \cap \Vert q\Vert )}$
. For other instances of sets and pairs of moment/history pairs
$R_{\mathbb {I}_a(\Vert p\Vert \cap \Vert q\Vert )}$
. For other instances of sets and pairs of moment/history pairs
![]() $\mathbb {C}_{suc}$
holds vacuously because the antecedent is always false.
$\mathbb {C}_{suc}$
holds vacuously because the antecedent is always false.
Since
![]() $\Vert p\Vert \in N_a((m'',h'))$
, it is the case that
$\Vert p\Vert \in N_a((m'',h'))$
, it is the case that
![]() $(m'',h')\in m_a(\Vert p\Vert )$
. So, the instances of
$(m'',h')\in m_a(\Vert p\Vert )$
. So, the instances of
![]() $\mathbb {C}_{suc}$
with the set
$\mathbb {C}_{suc}$
with the set
![]() $\Vert p\Vert $
and the pairs of moment/history pairs
$\Vert p\Vert $
and the pairs of moment/history pairs
![]() $((m,h'),((m'',h'))$
and
$((m,h'),((m'',h'))$
and
![]() $((m,h'),(m'',h'))$
are satisfied.
$((m,h'),(m'',h'))$
are satisfied.
Similarly, since
![]() $\Vert p\Vert \cap \Vert q\Vert \in N_a((m'',h'))$
it is the case that
$\Vert p\Vert \cap \Vert q\Vert \in N_a((m'',h'))$
it is the case that
![]() $(m'',h')\in m_a(\Vert p\Vert \cap \Vert q\Vert )$
. So the instances of
$(m'',h')\in m_a(\Vert p\Vert \cap \Vert q\Vert )$
. So the instances of
![]() $\mathbb {C}_{suc}$
with the set
$\mathbb {C}_{suc}$
with the set
![]() $\Vert p\Vert \cap \Vert q\Vert $
and the pairs of moment/history pairs
$\Vert p\Vert \cap \Vert q\Vert $
and the pairs of moment/history pairs
![]() $((m,h'),((m'',h'))$
and
$((m,h'),((m'',h'))$
and
![]() $((m,h'),(m'',h'))$
are satisfied.
$((m,h'),(m'',h'))$
are satisfied.
![]() $\mathbb {C}_{sim}$
is satisfied: we have it that
$\mathbb {C}_{sim}$
is satisfied: we have it that
![]() $(m,h')R_{\mathbb {I}_a \Vert p\Vert }(m'',h')$
but
$(m,h')R_{\mathbb {I}_a \Vert p\Vert }(m'',h')$
but
![]() $\Vert q\Vert \cap \Vert r\Vert \not \in N_a((m'',h'))$
. So,
$\Vert q\Vert \cap \Vert r\Vert \not \in N_a((m'',h'))$
. So,
![]() $(m'',h'))\not \in m_a(\Vert q\Vert \cap \Vert r\Vert )$
. So, the antecedent of the main implication in
$(m'',h'))\not \in m_a(\Vert q\Vert \cap \Vert r\Vert )$
. So, the antecedent of the main implication in
![]() $\mathbb {C}_{sim}$
is false, and thus the whole implication is true. Similarly if
$\mathbb {C}_{sim}$
is false, and thus the whole implication is true. Similarly if
![]() $(m,h')R_{\mathbb {I}_a \Vert p\Vert }(m'',h')$
. For each other combination of sets S of evaluation indices and pairs of moment/history pairs
$(m,h')R_{\mathbb {I}_a \Vert p\Vert }(m'',h')$
. For each other combination of sets S of evaluation indices and pairs of moment/history pairs
![]() $(x,y)$
, it is not the case that
$(x,y)$
, it is not the case that
![]() $xR_{\mathbb {I}_a S}y$
. So the antecedent and the consequent of the main implication are both vacuously true.
$xR_{\mathbb {I}_a S}y$
. So the antecedent and the consequent of the main implication are both vacuously true.
![]() $\mathbb {C}_{adj}$
is satisfied: We have to consider only the following instances: the one involving the set of evaluation indices
$\mathbb {C}_{adj}$
is satisfied: We have to consider only the following instances: the one involving the set of evaluation indices
![]() $\Vert p\Vert $
and the pairs of moment/history pairs
$\Vert p\Vert $
and the pairs of moment/history pairs
![]() $((m,h'),((m'',h'))$
and
$((m,h'),((m'',h'))$
and
![]() $((m,h'),(m'',h'))$
for these are the only pairs in
$((m,h'),(m'',h'))$
for these are the only pairs in
![]() $R_{\mathbb {I}_a \Vert p\Vert }$
; and the instance involving set
$R_{\mathbb {I}_a \Vert p\Vert }$
; and the instance involving set
![]() $\Vert p\Vert \cap \Vert q\Vert $
and the pairs of moment/history pairs
$\Vert p\Vert \cap \Vert q\Vert $
and the pairs of moment/history pairs
![]() $((m,h'),(m'',h')), $
and
$((m,h'),(m'',h')), $
and
![]() $((m,h'),(m'',h'))$
for these are the only elements of the relation
$((m,h'),(m'',h'))$
for these are the only elements of the relation
![]() $R_{\mathbb {I}_a(\Vert p\Vert \cap \Vert q\Vert )}$
. For other instances of sets and pairs of moment/history pairs
$R_{\mathbb {I}_a(\Vert p\Vert \cap \Vert q\Vert )}$
. For other instances of sets and pairs of moment/history pairs
![]() $\mathbb {C}_{adj}$
holds because the antecedent and consequent of the main implication are each vacuously true.
$\mathbb {C}_{adj}$
holds because the antecedent and consequent of the main implication are each vacuously true.
Since
![]() $\Vert q\Vert \cap \Vert r\Vert \not \in N_a((m'',h'))$
, it is not the case that
$\Vert q\Vert \cap \Vert r\Vert \not \in N_a((m'',h'))$
, it is not the case that
![]() $(m'',h')\in m_a(\Vert q\Vert \cap \Vert r\Vert )$
. So, the antecedent of the main implication is false for both
$(m'',h')\in m_a(\Vert q\Vert \cap \Vert r\Vert )$
. So, the antecedent of the main implication is false for both
![]() $((m,h'),((m'',h'))$
and
$((m,h'),((m'',h'))$
and
![]() $((m,h'),(m'',h'))$
, making
$((m,h'),(m'',h'))$
, making
![]() $\mathbb {C}_{adj}$
true.
$\mathbb {C}_{adj}$
true.
For set
![]() $\Vert p\Vert \cap \Vert q\Vert $
and the pairs of moment/history pairs
$\Vert p\Vert \cap \Vert q\Vert $
and the pairs of moment/history pairs
![]() $((m,h'),(m'',h'))$
and
$((m,h'),(m'',h'))$
and
![]() $((m,h'),(m'',h'))$
, we have the following. Since
$((m,h'),(m'',h'))$
, we have the following. Since
![]() $\Vert q\Vert \cap \Vert r\Vert \in N_a((m'',h'))$
it is true that
$\Vert q\Vert \cap \Vert r\Vert \in N_a((m'',h'))$
it is true that
![]() $(m'',h')\in m_a(\Vert q\Vert \cap \Vert r\Vert )$
. Hence the consequent of the main implication is true for both instances.
$(m'',h')\in m_a(\Vert q\Vert \cap \Vert r\Vert )$
. Hence the consequent of the main implication is true for both instances.
We now show that
![]() $\mathbb {C}_{cc}$
fails. By correspondence, it suffices to show that
$\mathbb {C}_{cc}$
fails. By correspondence, it suffices to show that
![]() $\mathcal {M}\nVdash (((A\wedge B)[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
. We show that
$\mathcal {M}\nVdash (((A\wedge B)[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
. We show that
![]() $\mathcal {M}, (m,h')\vDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
,
$\mathcal {M}, (m,h')\vDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
,
![]() $\mathcal {M}, (m,h')\vDash p[a]\!\!\!\rightarrow \! q$
and
$\mathcal {M}, (m,h')\vDash p[a]\!\!\!\rightarrow \! q$
and
![]() $\mathcal {M}, (m,h')\nvDash p[a]\!\!\!\rightarrow \! r$
. We have by Lemma 5.21 that
$\mathcal {M}, (m,h')\nvDash p[a]\!\!\!\rightarrow \! r$
. We have by Lemma 5.21 that
 $(m,h')R_{\Vert I_a(p\wedge q)\Vert }(m'',h')$
. By construction we have
$(m,h')R_{\Vert I_a(p\wedge q)\Vert }(m'',h')$
. By construction we have
![]() $\Vert r\Vert \in N_a((m'',h'))$
. So,
$\Vert r\Vert \in N_a((m'',h'))$
. So,
![]() $\mathcal {M}, (m'',h')\vDash \square _a r$
. Moreover,
$\mathcal {M}, (m'',h')\vDash \square _a r$
. Moreover,
![]() $c(r)\sqsubseteq c(p)\sqsubseteq c(p\wedge q)$
. Hence,
$c(r)\sqsubseteq c(p)\sqsubseteq c(p\wedge q)$
. Hence,
![]() $\mathcal {M}, (m,h')\vDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
. We have by Lemma 5.21 that
$\mathcal {M}, (m,h')\vDash (p\wedge q)[a]\!\!\!\rightarrow \! r$
. We have by Lemma 5.21 that
![]() $(m,h')R_{\Vert I_a p\Vert }(m'',h')$
. By construction we have
$(m,h')R_{\Vert I_a p\Vert }(m'',h')$
. By construction we have
![]() $\Vert q\Vert \in N_a((m'',h'))$
. So,
$\Vert q\Vert \in N_a((m'',h'))$
. So,
![]() $\mathcal {M}, (m'',h')\vDash \square _a q$
. Moreover,
$\mathcal {M}, (m'',h')\vDash \square _a q$
. Moreover,
![]() $c(q)\sqsubseteq c(p)$
. Hence,
$c(q)\sqsubseteq c(p)$
. Hence,
![]() $\mathcal {M}, (m,h')\vDash p[a]\!\!\!\rightarrow \! q$
. We have by Lemma 5.21 that
$\mathcal {M}, (m,h')\vDash p[a]\!\!\!\rightarrow \! q$
. We have by Lemma 5.21 that
![]() $(m,h')R_{\Vert I_a p\Vert }(m'',h')$
. By construction we have
$(m,h')R_{\Vert I_a p\Vert }(m'',h')$
. By construction we have
![]() $\Vert r\Vert \not \in N_a((m'',h'))$
. So,
$\Vert r\Vert \not \in N_a((m'',h'))$
. So,
![]() $\mathcal {M}, (m'',h')\nvDash \square _a r$
. Moreover,
$\mathcal {M}, (m'',h')\nvDash \square _a r$
. Moreover,
![]() $c(q)\sqsubseteq c(p)$
. Hence,
$c(q)\sqsubseteq c(p)$
. Hence,
![]() $\mathcal {M}, (m,h')\nvDash p[a]\!\!\!\rightarrow \! r$
. Therefore,
$\mathcal {M}, (m,h')\nvDash p[a]\!\!\!\rightarrow \! r$
. Therefore,
![]() $\mathcal {M}\nVdash (((A\wedge B)[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
and hence
$\mathcal {M}\nVdash (((A\wedge B)[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
and hence
![]() $\mathcal {F}\nVdash (((A\wedge B)[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
. By Proposition 5.26,
$\mathcal {F}\nVdash (((A\wedge B)[a]\!\!\!\rightarrow \! C)\wedge (A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C)$
. By Proposition 5.26,
![]() $\mathcal {F}$
doesn’t satisfy
$\mathcal {F}$
doesn’t satisfy
![]() $\mathbb {C}_{cc}$
. (Figure A.6) shows a graphical countermodel, where the thin arrows indicate the ordering between the moments (we omit reflexive arrows), and we chose dashed and dotted lines for different accessibility relations. Note that
$\mathbb {C}_{cc}$
. (Figure A.6) shows a graphical countermodel, where the thin arrows indicate the ordering between the moments (we omit reflexive arrows), and we chose dashed and dotted lines for different accessibility relations. Note that
![]() $h'$
(
$h'$
(
![]() $h'$
) passes through m and
$h'$
) passes through m and
![]() $m'$
(
$m'$
(
![]() $m'$
).Footnote
28
$m'$
).Footnote
28
Proposition 5.31. Let
![]() $\mathcal {F}$
be a frame such that
$\mathcal {F}$
be a frame such that
![]() $\mathcal {F} \Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
,
$\mathcal {F} \Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! B)$
,
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! C)$
, and
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! (B\wedge C))\supset (A[a]\!\!\!\rightarrow \! C)$
, and
![]() $\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! B)\supset ((A[a]\!\!\!\rightarrow \! C)\supset (A[a]\!\!\!\rightarrow \! (B\wedge C)$
. Then
$\mathcal {F}\Vdash (A[a]\!\!\!\rightarrow \! B)\supset ((A[a]\!\!\!\rightarrow \! C)\supset (A[a]\!\!\!\rightarrow \! (B\wedge C)$
. Then
![]() $\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! (B\supset C)) \supset ((A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C))$
.
$\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! (B\supset C)) \supset ((A[a]\!\!\!\rightarrow \! B))\supset (A[a]\!\!\!\rightarrow \! C))$
.

Fig. A.6 Countermodel cautious cut.
Proof. Let
![]() $\mathcal {F}$
be a frame as in the assumption of the proposition. By frame correspondence,
$\mathcal {F}$
be a frame as in the assumption of the proposition. By frame correspondence,
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{sim}$
and
$\mathbb {C}_{sim}$
and
![]() $\mathbb {C}_{adj}$
.
$\mathbb {C}_{adj}$
.
Let
![]() $\mathcal {M}$
be based on
$\mathcal {M}$
be based on
![]() $\mathcal {F}$
and let
$\mathcal {F}$
and let
![]() $(m,h)\in \mathcal {M}$
be such that
$(m,h)\in \mathcal {M}$
be such that
![]() $\mathcal {M}, (m,h)\vDash [A]B$
and
$\mathcal {M}, (m,h)\vDash [A]B$
and
![]() $\mathcal {M}, (m,h)\vDash [A](B\supset C)$
. By the former, we have
$\mathcal {M}, (m,h)\vDash [A](B\supset C)$
. By the former, we have
![]() $\Vert B\Vert \in N_a((m,h'))$
for each
$\Vert B\Vert \in N_a((m,h'))$
for each
![]() $(m,h')$
that is accessible from
$(m,h')$
that is accessible from
![]() $(m,h)$
by
$(m,h)$
by
![]() $R_{\Vert I_a A\Vert }$
. By the second assumption, we have
$R_{\Vert I_a A\Vert }$
. By the second assumption, we have
![]() $\Vert B\supset C \Vert \in N_a((m,h'))$
for each
$\Vert B\supset C \Vert \in N_a((m,h'))$
for each
![]() $(m,h')$
that is accessible from
$(m,h')$
that is accessible from
![]() $(m,h)$
by
$(m,h)$
by
![]() $R_{\Vert I_a A\Vert }$
. Consider an arbitrary
$R_{\Vert I_a A\Vert }$
. Consider an arbitrary
![]() $(m,h')$
such that
$(m,h')$
such that
![]() $(m,h)R_{\Vert I_a A\Vert }(m,h')$
. So,
$(m,h)R_{\Vert I_a A\Vert }(m,h')$
. So,
![]() $\Vert B\Vert \in N_a((m,h'))$
and
$\Vert B\Vert \in N_a((m,h'))$
and
![]() $\Vert B\supset C \Vert \in N_a((m,h'))$
. The latter entails that that
$\Vert B\supset C \Vert \in N_a((m,h'))$
. The latter entails that that
![]() $\Vert \neg B\Vert \cup \Vert C\Vert \in N_a((m,h'))$
since we are dealing with material implication. By
$\Vert \neg B\Vert \cup \Vert C\Vert \in N_a((m,h'))$
since we are dealing with material implication. By
![]() $\mathbb {C}_{adj}$
, it follows that
$\mathbb {C}_{adj}$
, it follows that
![]() $\Vert B\Vert \cap (\Vert \neg B\Vert \cup \Vert C\Vert )$
, which is just
$\Vert B\Vert \cap (\Vert \neg B\Vert \cup \Vert C\Vert )$
, which is just
![]() $\Vert B\Vert \cap \Vert C\Vert $
, belongs to
$\Vert B\Vert \cap \Vert C\Vert $
, belongs to
![]() $N_a((m,h'))$
. By
$N_a((m,h'))$
. By
![]() $\mathbb {C}_{sim}$
it follows that
$\mathbb {C}_{sim}$
it follows that
![]() $\Vert C\Vert \in N_a((m,h'))$
. So,
$\Vert C\Vert \in N_a((m,h'))$
. So,
![]() $\mathcal {M}, (m,h')\vDash \square _a C$
and hence
$\mathcal {M}, (m,h')\vDash \square _a C$
and hence
![]() $\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
. Since we considered an arbitrary world
$\mathcal {M}, (m,h)\vDash A[a]\!\!\!\rightarrow \! C$
. Since we considered an arbitrary world
![]() $(m,h)$
in
$(m,h)$
in
![]() $\mathcal {M}$
, it follows that
$\mathcal {M}$
, it follows that
![]() $\mathcal {M}\Vdash ((A[a]\!\!\!\rightarrow \! B)\wedge (A[a]\!\!\!\rightarrow \! (B\supset C))\supset (A[a]\!\!\!\rightarrow \! C)$
. Since the model based on
$\mathcal {M}\Vdash ((A[a]\!\!\!\rightarrow \! B)\wedge (A[a]\!\!\!\rightarrow \! (B\supset C))\supset (A[a]\!\!\!\rightarrow \! C)$
. Since the model based on
![]() $\mathcal {F}$
was arbitrary,
$\mathcal {F}$
was arbitrary,
![]() $\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! B)\wedge (A[a]\!\!\!\rightarrow \! (B\supset C))\supset (A[a]\!\!\!\rightarrow \! C)$
. (By frame correspondence,
$\mathcal {F}\Vdash ((A[a]\!\!\!\rightarrow \! B)\wedge (A[a]\!\!\!\rightarrow \! (B\supset C))\supset (A[a]\!\!\!\rightarrow \! C)$
. (By frame correspondence,
![]() $\mathcal {F}$
satisfies
$\mathcal {F}$
satisfies
![]() $\mathbb {C}_{CII}$
.)
$\mathbb {C}_{CII}$
.)
Indeterminacy
Proposition 5.32.
![]() $\not\models (A[a]\!\!\!\rightarrow \! (B\!\vee\! C))\!\supset\! ((A[a]\!\!\!\rightarrow \! B) \!\vee\! (A[a]\!\!\!\rightarrow \! C))$
.
$\not\models (A[a]\!\!\!\rightarrow \! (B\!\vee\! C))\!\supset\! ((A[a]\!\!\!\rightarrow \! B) \!\vee\! (A[a]\!\!\!\rightarrow \! C))$
.
Proof. We define
![]() $\mathcal {M}$
as follows: let
$\mathcal {M}$
as follows: let
![]() $Tree= \lbrace m, n, m'\rbrace $
,
$Tree= \lbrace m, n, m'\rbrace $
,
![]() $\leq =\lbrace (m,m)$
,
$\leq =\lbrace (m,m)$
,
![]() $(n,n)$
,
$(n,n)$
,
![]() $(m'',m')$
,
$(m'',m')$
,
![]() $(m,n)$
,
$(m,n)$
,
![]() $(m, m')\rbrace $
,
$(m, m')\rbrace $
,
![]() $Ag=\lbrace a \rbrace $
. So
$Ag=\lbrace a \rbrace $
. So
![]() $h=(m,n), h'=(m, m')$
. Let
$h=(m,n), h'=(m, m')$
. Let
![]() $v(p)=\lbrace (n,h)\rbrace , v(q)=\lbrace (m,h')\rbrace $
,
$v(p)=\lbrace (n,h)\rbrace , v(q)=\lbrace (m,h')\rbrace $
,
![]() $v(r)=\lbrace (m,h')\rbrace $
. Let
$v(r)=\lbrace (m,h')\rbrace $
. Let
![]() $c(q)\sqsubseteq c(p)$
and
$c(q)\sqsubseteq c(p)$
and
![]() $c(r)\sqsubseteq c(p)$
. Let
$c(r)\sqsubseteq c(p)$
. Let
![]() $Choice:a^m(h)=\lbrace h\rbrace $
,
$Choice:a^m(h)=\lbrace h\rbrace $
,
![]() $Choice:a^m(h')=Choice:a^m(h)=\lbrace h'', h\rbrace $
. Let
$Choice:a^m(h')=Choice:a^m(h)=\lbrace h'', h\rbrace $
. Let
![]() $N_a((m,h))=\varnothing $
,
$N_a((m,h))=\varnothing $
,
![]() $N_a((m,h'))=\lbrace \Vert p\Vert , \Vert q\Vert , \Vert q\vee r\Vert \rbrace $
,
$N_a((m,h'))=\lbrace \Vert p\Vert , \Vert q\Vert , \Vert q\vee r\Vert \rbrace $
,
![]() $N_a((m,h'))=\lbrace \Vert p\Vert , \Vert r\Vert , \Vert q\vee r\Vert \rbrace $
. Let
$N_a((m,h'))=\lbrace \Vert p\Vert , \Vert r\Vert , \Vert q\vee r\Vert \rbrace $
. Let
![]() $R_{\Vert I_a p\Vert }=\lbrace ((m,h),(m,h')), ((m,h),(m,h'))\rbrace $
. Note that
$R_{\Vert I_a p\Vert }=\lbrace ((m,h),(m,h')), ((m,h),(m,h'))\rbrace $
. Note that
![]() $\mathcal {M}, (m,h')\vDash I_a p$
. The histories
$\mathcal {M}, (m,h')\vDash I_a p$
. The histories
![]() $h'',h\in Choice:a^m(h')=Choice:a^m(h)$
are the only elements to consider in each case. We have
$h'',h\in Choice:a^m(h')=Choice:a^m(h)$
are the only elements to consider in each case. We have
![]() $\Vert p\Vert \in N_a((m,h'))$
and
$\Vert p\Vert \in N_a((m,h'))$
and
![]() $\Vert p\Vert \in N_a((m,h'))$
. But also
$\Vert p\Vert \in N_a((m,h'))$
. But also
![]() $\Vert p\Vert \not \in N_a((m,h))$
. We need to show that
$\Vert p\Vert \not \in N_a((m,h))$
. We need to show that
![]() $\mathcal {M} ,(m,h)\vDash p[a]\!\!\!\rightarrow \! (q\vee r)$
and
$\mathcal {M} ,(m,h)\vDash p[a]\!\!\!\rightarrow \! (q\vee r)$
and
![]() $\mathcal {M}, (m,h)\nvDash (p[a]\!\!\!\rightarrow \! q)\vee (p[a]\!\!\!\rightarrow \! r)$
. Since
$\mathcal {M}, (m,h)\nvDash (p[a]\!\!\!\rightarrow \! q)\vee (p[a]\!\!\!\rightarrow \! r)$
. Since
![]() $\Vert q \vee r\Vert \in N_a((m,h'))$
, we have it that
$\Vert q \vee r\Vert \in N_a((m,h'))$
, we have it that
![]() $\mathcal {M}, (m,h')\vDash \square _a (q\vee r)$
. Similarly
$\mathcal {M}, (m,h')\vDash \square _a (q\vee r)$
. Similarly
![]() $\mathcal {M}, (m,h')\vDash \square _a (q\vee r)$
. Since these are the only worlds accessible via
$\mathcal {M}, (m,h')\vDash \square _a (q\vee r)$
. Since these are the only worlds accessible via
![]() $R_{\Vert I_a p\Vert }$
, this establishes
$R_{\Vert I_a p\Vert }$
, this establishes
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! (q\vee r)$
. We have that
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! (q\vee r)$
. We have that
![]() $(m,h)R_{\Vert I_a p\Vert }(m,h')$
. Since
$(m,h)R_{\Vert I_a p\Vert }(m,h')$
. Since
![]() $\Vert r\Vert \notin N_a((m,h'))$
,
$\Vert r\Vert \notin N_a((m,h'))$
,
![]() $\mathcal {M}, (m,h')\nvDash \square _a r$
. Hence
$\mathcal {M}, (m,h')\nvDash \square _a r$
. Hence
![]() $\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! r$
. Similarly for the other disjunct.
$\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! r$
. Similarly for the other disjunct.
Non-monotonicity
Proposition 5.33.
![]() $\not \models (A[a]\!\!\!\rightarrow \! B)\supset ((A\wedge C)[a]\!\!\!\rightarrow \! B)$
.
$\not \models (A[a]\!\!\!\rightarrow \! B)\supset ((A\wedge C)[a]\!\!\!\rightarrow \! B)$
.
Proof. We define
![]() $\mathcal {M}$
as before. We show that
$\mathcal {M}$
as before. We show that
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
and
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
and
![]() $\mathcal {M}, (m,h)\nvDash (p\wedge r)[a]\!\!\!\rightarrow \! q$
. As for the former, the only pair to consider is
$\mathcal {M}, (m,h)\nvDash (p\wedge r)[a]\!\!\!\rightarrow \! q$
. As for the former, the only pair to consider is
![]() $(m,h')$
for it is the only one accessible via
$(m,h')$
for it is the only one accessible via
![]() $R_{\Vert I_a p\Vert }$
. Since
$R_{\Vert I_a p\Vert }$
. Since
![]() $\Vert q\Vert \in N_a((m,h'))$
,
$\Vert q\Vert \in N_a((m,h'))$
,
![]() $\mathcal {M}, (m,h')\vDash \square _a q$
, which is what we needed to show. To show that
$\mathcal {M}, (m,h')\vDash \square _a q$
, which is what we needed to show. To show that
![]() $\mathcal {M}, (m,h)\nvDash (p\wedge r)[a]\!\!\!\rightarrow \! q$
we only have to consider
$\mathcal {M}, (m,h)\nvDash (p\wedge r)[a]\!\!\!\rightarrow \! q$
we only have to consider
![]() $(m,h')$
since it’s the only accessible pair via
$(m,h')$
since it’s the only accessible pair via
![]() $R_{\Vert I_a (p\wedge r)\Vert }$
. Since
$R_{\Vert I_a (p\wedge r)\Vert }$
. Since
![]() $\Vert q\Vert \notin N_a((m,h'))$
, it follows that
$\Vert q\Vert \notin N_a((m,h'))$
, it follows that
![]() $\mathcal {M}, (m,h')\nvDash \square _a q$
, which is what we needed to show. We leave the graphical countermodel as an exercise.
$\mathcal {M}, (m,h')\nvDash \square _a q$
, which is what we needed to show. We leave the graphical countermodel as an exercise.
Non-explosiveness
Proposition 5.34.
![]() $\not \models (A\wedge \neg A)[a]\!\!\!\rightarrow \! B$
.
$\not \models (A\wedge \neg A)[a]\!\!\!\rightarrow \! B$
.
Proof. We define
![]() $\mathcal {M}$
as follows: let
$\mathcal {M}$
as follows: let
![]() $Tree= \lbrace m, n, m'\rbrace $
,
$Tree= \lbrace m, n, m'\rbrace $
,
![]() $\leq =\lbrace (m,m)$
,
$\leq =\lbrace (m,m)$
,
![]() $(n,n)$
,
$(n,n)$
,
![]() $(m'',m')$
,
$(m'',m')$
,
![]() $(m,n)$
,
$(m,n)$
,
![]() $(m, m')\rbrace $
,
$(m, m')\rbrace $
,
![]() $Ag=\lbrace a \rbrace $
. So
$Ag=\lbrace a \rbrace $
. So
![]() $h=(m,n), h'=(m, m')$
. And let
$h=(m,n), h'=(m, m')$
. And let
![]() $v(p)=\lbrace (n,h)\rbrace , v(q)=\lbrace (m,h')\rbrace $
. Let
$v(p)=\lbrace (n,h)\rbrace , v(q)=\lbrace (m,h')\rbrace $
. Let
![]() $c(q)\not \sqsubseteq c(p)$
. Let
$c(q)\not \sqsubseteq c(p)$
. Let
![]() $Choice:a^m(h)=\lbrace h\rbrace $
,
$Choice:a^m(h)=\lbrace h\rbrace $
,
![]() $Choice:a^m(h')=\lbrace h'\rbrace $
. Let
$Choice:a^m(h')=\lbrace h'\rbrace $
. Let
![]() $N_a((m,h))=\varnothing $
,
$N_a((m,h))=\varnothing $
,
![]() $N_a((m,h'))=\lbrace \Vert p\Vert , \Vert q\Vert \rbrace $
. Let
$N_a((m,h'))=\lbrace \Vert p\Vert , \Vert q\Vert \rbrace $
. Let
![]() $R_{\Vert I_a p\Vert }=\lbrace ((m,h),(m,h'))\rbrace $
. To show that
$R_{\Vert I_a p\Vert }=\lbrace ((m,h),(m,h'))\rbrace $
. To show that
![]() $\mathcal {M}, (m,h)\nvDash (p\wedge \neg p)[a]\!\!\!\rightarrow \! q$
, observe that this is just showing that
$\mathcal {M}, (m,h)\nvDash (p\wedge \neg p)[a]\!\!\!\rightarrow \! q$
, observe that this is just showing that
![]() . Since
. Since
![]() $c(q)\not \sqsubseteq c(p)$
and since
$c(q)\not \sqsubseteq c(p)$
and since
![]() $c(\square _a q)=c(q)$
, also
$c(\square _a q)=c(q)$
, also
![]() $c(\square _a q)\not \sqsubseteq c(p)$
. This falsifies the second condition for truth-condition of
$c(\square _a q)\not \sqsubseteq c(p)$
. This falsifies the second condition for truth-condition of
![]() .
.
Relevance
Proposition 5.35.
![]() $\not \models (A[a]\!\!\!\rightarrow \! B)\supset (A[a]\!\!\!\rightarrow \! (B\vee C))$
.
$\not \models (A[a]\!\!\!\rightarrow \! B)\supset (A[a]\!\!\!\rightarrow \! (B\vee C))$
.
Proof. We define
![]() $\mathcal {M}$
as follows: let
$\mathcal {M}$
as follows: let
![]() $Tree= \lbrace m, n, m'\rbrace $
,
$Tree= \lbrace m, n, m'\rbrace $
,
![]() $\leq =\lbrace (m,m)$
,
$\leq =\lbrace (m,m)$
,
![]() $(n,n)$
,
$(n,n)$
,
![]() $(m'',m')$
,
$(m'',m')$
,
![]() $(m,n)$
,
$(m,n)$
,
![]() $(m, m')\rbrace $
,
$(m, m')\rbrace $
,
![]() $Ag=\lbrace a \rbrace $
. So
$Ag=\lbrace a \rbrace $
. So
![]() $h=(m,n), h'=(m, m')$
. And let
$h=(m,n), h'=(m, m')$
. And let
![]() $v(p)=\lbrace (n,h)\rbrace , v(q)=\lbrace (m,h')\rbrace $
,
$v(p)=\lbrace (n,h)\rbrace , v(q)=\lbrace (m,h')\rbrace $
,
![]() $v(r)=\lbrace (m,h)\rbrace $
. Let
$v(r)=\lbrace (m,h)\rbrace $
. Let
![]() $c(q)\sqsubseteq c(p)$
and
$c(q)\sqsubseteq c(p)$
and
![]() $c(p)\sqsubset c(r)$
, i.e.
$c(p)\sqsubset c(r)$
, i.e.
![]() $c(r)\not \subseteq c(p)$
. Let
$c(r)\not \subseteq c(p)$
. Let
![]() $Choice:a^m(h)=\lbrace h\rbrace $
,
$Choice:a^m(h)=\lbrace h\rbrace $
,
![]() $Choice:a^m(h')=\lbrace h'\rbrace $
. Let
$Choice:a^m(h')=\lbrace h'\rbrace $
. Let
![]() $N_a((m,h))=\varnothing $
,
$N_a((m,h))=\varnothing $
,
![]() $N_a((m,h'))=\lbrace \Vert p\Vert , \Vert q\Vert \rbrace $
. Let
$N_a((m,h'))=\lbrace \Vert p\Vert , \Vert q\Vert \rbrace $
. Let
![]() $R_{\Vert I_a p\Vert }=\lbrace ((m,h),(m,h'))\rbrace $
. Again it is straightforward to see that
$R_{\Vert I_a p\Vert }=\lbrace ((m,h),(m,h'))\rbrace $
. Again it is straightforward to see that
![]() $\mathcal {M}, (m,h')\vDash I_a p$
. We show that
$\mathcal {M}, (m,h')\vDash I_a p$
. We show that
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
. The only accessible pair via
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! q$
. The only accessible pair via
![]() $R_{\Vert I_a p\Vert }$
is
$R_{\Vert I_a p\Vert }$
is
![]() $(m,h')$
. Since
$(m,h')$
. Since
![]() $\Vert q\Vert \in N_a((m,h'))$
it holds that
$\Vert q\Vert \in N_a((m,h'))$
it holds that
![]() $\mathcal {M}, (m,h')\vDash \square _a q$
. Moreover
$\mathcal {M}, (m,h')\vDash \square _a q$
. Moreover
![]() $c(q)\sqsubseteq c(p)$
. To show that
$c(q)\sqsubseteq c(p)$
. To show that
![]() $\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! (q\vee r)$
, observe that
$\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! (q\vee r)$
, observe that
![]() $c(\square _a (q\vee r))=c(q\vee r)=c(q)\oplus c(r)$
. Since
$c(\square _a (q\vee r))=c(q\vee r)=c(q)\oplus c(r)$
. Since
![]() $c(r)\not \sqsubseteq c(p)$
, also
$c(r)\not \sqsubseteq c(p)$
, also
![]() $c(q)\oplus c(r)\not \sqsubseteq c(p)$
. According to the definition of truth,
$c(q)\oplus c(r)\not \sqsubseteq c(p)$
. According to the definition of truth,
![]() $\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! (q\vee r)$
iff
$\mathcal {M}, (m,h)\vDash p[a]\!\!\!\rightarrow \! (q\vee r)$
iff
![]() and
and
![]() $c(\square _a (q\vee r))\sqsubseteq c(p)$
. But the second conjunct is not satisfied. Hence,
$c(\square _a (q\vee r))\sqsubseteq c(p)$
. But the second conjunct is not satisfied. Hence,
![]() $\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! (q\vee r)$
.
$\mathcal {M}, (m,h)\nvDash p[a]\!\!\!\rightarrow \! (q\vee r)$
.