No CrossRef data available.
Article contents
SET THEORY AND A MODEL OF THE MIND IN PSYCHOLOGY
Published online by Cambridge University Press: 14 March 2022
Abstract
We investigate the mathematics of a model of the human mind which has been proposed by the psychologist Jens Mammen. Mathematical realizations of this model consists of what the first author (A.T.) has called Mammen spaces, where a Mammen space is a triple 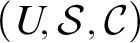 $(U,\mathcal S,\mathcal C)$, where U is a non-empty set (“the universe”),
$(U,\mathcal S,\mathcal C)$, where U is a non-empty set (“the universe”), 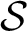 $\mathcal S$ is a perfect Hausdorff topology on U, and
$\mathcal S$ is a perfect Hausdorff topology on U, and 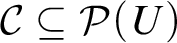 $\mathcal C\subseteq \mathcal P(U)$ together with
$\mathcal C\subseteq \mathcal P(U)$ together with 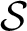 $\mathcal S$ satisfy certain axioms.
$\mathcal S$ satisfy certain axioms.
We refute a conjecture put forward by Hoffmann-Jørgensen, who conjectured that the existence of a “complete” Mammen space implies the Axiom of Choice, by showing that in the first Cohen model, in which ZF holds but AC fails, there is a complete Mammen space. We obtain this by proving that in the first Cohen model, every perfect topology can be extended to a maximal perfect topology.
On the other hand, we also show that if all sets are Lebesgue measurable, or all sets are Baire measurable, then there are no complete Mammen spaces with a countable universe.
Further, we investigate two new cardinal invariants 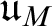 $\mathfrak u_{M}$ and
$\mathfrak u_{M}$ and 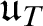 $\mathfrak u_{T}$ associated with complete Mammen spaces and maximal perfect topologies, and establish some basic inequalities that are provable in ZFC. Then we show
$\mathfrak u_{T}$ associated with complete Mammen spaces and maximal perfect topologies, and establish some basic inequalities that are provable in ZFC. Then we show 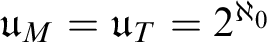 $\mathfrak u_{M}=\mathfrak u_{T}=2^{\aleph _{0}}$ follows from Martin’s Axiom, and, contrastingly, we show that
$\mathfrak u_{M}=\mathfrak u_{T}=2^{\aleph _{0}}$ follows from Martin’s Axiom, and, contrastingly, we show that 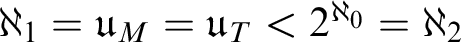 $\aleph _{1}=\mathfrak u_{M}=\mathfrak u_{T}<2^{\aleph _{0}}=\aleph _{2}$ in the Baumgartner–Laver model.
$\aleph _{1}=\mathfrak u_{M}=\mathfrak u_{T}<2^{\aleph _{0}}=\aleph _{2}$ in the Baumgartner–Laver model.
Finally, consequences for psychology are discussed.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


