1 Introduction
The question whether there are nonclassical formal systems of primitive truth that can achieve significant proof-theoretic strength has received much attention in the recent literature. Solomon Feferman [Reference Feferman3] famously claimed that ‘nothing like sustained ordinary reasoning can be carried on’ in the standard nonclassical systems that support strong forms of inter-substitutivity of A and ‘“A” is true’. One way of understanding this claim is by measuring how much mathematics can be encoded in such systems. Since the strength of mathematical systems (whether classical or nonclassical) is traditionally measured in terms of the ordinals that can be well-ordered by them, the ordinal analysis of nonclassical systems of truth becomes relevant.
We are mainly interested in the proof-theoretic analysis of nonclassical systems inspired by fixed-point semantics [Reference Kripke18]. Since fixed-point semantics has nice axiomatizations, both classical and nonclassical, it represents a particularly convenient arena to measure the impact of weakening the logic on proof-theoretic strength. The axiomatization of fixed-point semantics in classical logic—a.k.a.
![]() $\textbf {KF}$
—is known to have the proof-theoretic ordinal
$\textbf {KF}$
—is known to have the proof-theoretic ordinal
![]() $\varphi _{\varepsilon _0}0$
[Reference Cantini1, Reference Feferman4].Footnote
1
Halbach and Horsten have proposed in [Reference Halbach and Horsten15] a nonclassical axiomatization, known as
$\varphi _{\varepsilon _0}0$
[Reference Cantini1, Reference Feferman4].Footnote
1
Halbach and Horsten have proposed in [Reference Halbach and Horsten15] a nonclassical axiomatization, known as
![]() $\textbf {PKF}$
, and showed that it has proof-theoretic ordinal
$\textbf {PKF}$
, and showed that it has proof-theoretic ordinal
![]() $\varphi _{\omega } 0$
. There have been some attempts to overcome this mismatch in strength on the nonclassical side. Nicolai [Reference Nicolai22] showed that even without expanding the logical resources of the theory,
$\varphi _{\omega } 0$
. There have been some attempts to overcome this mismatch in strength on the nonclassical side. Nicolai [Reference Nicolai22] showed that even without expanding the logical resources of the theory,
![]() $\textbf {PKF}$
can be extended with suitable instances of transfinite induction to recover all classical true theorems of
$\textbf {PKF}$
can be extended with suitable instances of transfinite induction to recover all classical true theorems of
![]() $\textbf {KF}$
. Fischer et al. [Reference Fischer, Horsten and Nicolai10] showed that a simple theory featuring nonclassical initial sequents of the form
$\textbf {KF}$
. Fischer et al. [Reference Fischer, Horsten and Nicolai10] showed that a simple theory featuring nonclassical initial sequents of the form
![]() $A\Rightarrow \texttt {Tr}\ulcorner A\urcorner $
and
$A\Rightarrow \texttt {Tr}\ulcorner A\urcorner $
and
![]() $\texttt {Tr}\ulcorner A\urcorner \Rightarrow A$
can be closed under special reflection principles to recover the arithmetical strength of
$\texttt {Tr}\ulcorner A\urcorner \Rightarrow A$
can be closed under special reflection principles to recover the arithmetical strength of
![]() $\textbf {PKF}$
and
$\textbf {PKF}$
and
![]() $\textbf {KF}$
. More recently, Field showed in [Reference Field8] that, by enlarging the primitive concepts of
$\textbf {KF}$
. More recently, Field showed in [Reference Field8] that, by enlarging the primitive concepts of
![]() $\textbf {PKF}$
with a predicate for ‘classicality’, one can achieve the proof-theoretic strength of
$\textbf {PKF}$
with a predicate for ‘classicality’, one can achieve the proof-theoretic strength of
![]() $\textbf {KF}$
in both the schematic and non-schematic versions.
$\textbf {KF}$
in both the schematic and non-schematic versions.
In the paper we explore a different option, which in a sense completes the picture above. We enlarge the standard four-valued logic of
![]() $\textbf {PKF}$
with a new conditional, which is based on the logic
$\textbf {PKF}$
with a new conditional, which is based on the logic
![]() $\mathbf {HYPE}$
recently proposed by [Reference Leitgeb19]. The conditional has several features that resemble an intuitionistic conditional, but its weaker interaction with the
$\mathbf {HYPE}$
recently proposed by [Reference Leitgeb19]. The conditional has several features that resemble an intuitionistic conditional, but its weaker interaction with the
![]() $\mathbf {FDE}$
-negation makes it possible to sustain the intersubstitutivity of A and ‘“A” is true’ for sentences not containing the conditional. This extended theory, that we call
$\mathbf {FDE}$
-negation makes it possible to sustain the intersubstitutivity of A and ‘“A” is true’ for sentences not containing the conditional. This extended theory, that we call
![]() ${\textbf {KFL}}$
, is shown to be proof-theoretically equivalent to
${\textbf {KFL}}$
, is shown to be proof-theoretically equivalent to
![]() $\textbf {KF}$
. Its extension with a schematic substitution rule, called
$\textbf {KF}$
. Its extension with a schematic substitution rule, called
![]() $\textbf {KFL}^{*}$
, is shown to be proof-theoretically equivalent to the schematic extension of
$\textbf {KFL}^{*}$
, is shown to be proof-theoretically equivalent to the schematic extension of
![]() $\textbf {KF}$
—called
$\textbf {KF}$
—called
![]() $\texttt {Ref}^*(\texttt {PA}(P))$
in [Reference Feferman4].
$\texttt {Ref}^*(\texttt {PA}(P))$
in [Reference Feferman4].
In particular, we show that the conditional of the logic
![]() $\mathbf {HYPE}$
enables one to mimic, when carefully handled, the standard lower bound proofs by Gentzen and Feferman–Schütte for transfinite induction in classical arithmetic (Theorem 1) and predicative analysis (Proposition 4), respectively. This enables us to define, in our theories
$\mathbf {HYPE}$
enables one to mimic, when carefully handled, the standard lower bound proofs by Gentzen and Feferman–Schütte for transfinite induction in classical arithmetic (Theorem 1) and predicative analysis (Proposition 4), respectively. This enables us to define, in our theories
![]() ${\textbf {KFL}}$
and
${\textbf {KFL}}$
and
![]() $\textbf {KFL}^{*}$
, ramified truth predicates indexed by ordinals smaller than
$\textbf {KFL}^{*}$
, ramified truth predicates indexed by ordinals smaller than
![]() $\varepsilon _0$
(Corollary 4) and
$\varepsilon _0$
(Corollary 4) and
![]() $\Gamma _0$
(Corollary 7). Moreover, the proof-theoretic analysis of
$\Gamma _0$
(Corollary 7). Moreover, the proof-theoretic analysis of
![]() ${\textbf {KFL}}$
and
${\textbf {KFL}}$
and
![]() $\textbf {KFL}^{*}$
is completed by showing that their truth predicates can be suitably interpreted in their classical counterparts
$\textbf {KFL}^{*}$
is completed by showing that their truth predicates can be suitably interpreted in their classical counterparts
![]() $\textbf {KF}$
and
$\textbf {KF}$
and
![]() $\texttt {Ref}^*(\texttt {PA}(P))$
without altering the arithmetical vocabulary (Propositions 2 and 5).
$\texttt {Ref}^*(\texttt {PA}(P))$
without altering the arithmetical vocabulary (Propositions 2 and 5).
2 HYPE
In this section we will present the logical basis of our systems of truth. We will work with a sequent calculus variant of the logic
![]() $\mathbf {HYPE}$
introduced by Leitgeb in [Reference Leitgeb19] by means of a Hilbert style calculus. Essentially, the calculus is obtained by extending First-Degree Entailment with an intuitionistic conditional and with rules for it in a multi-conclusion style.
$\mathbf {HYPE}$
introduced by Leitgeb in [Reference Leitgeb19] by means of a Hilbert style calculus. Essentially, the calculus is obtained by extending First-Degree Entailment with an intuitionistic conditional and with rules for it in a multi-conclusion style.
2.1
 $\mathbf{G1h_{cd}}$
$\mathbf{G1h_{cd}}$
We present a multi-conclusion system based on a multi-conclusion calculus for intuitionistic logic:Footnote
2
we call it
![]() $\mathbf {G1h}_{\mathbf {cd}}$
for Gentzen system for the logic
$\mathbf {G1h}_{\mathbf {cd}}$
for Gentzen system for the logic
![]() $\mathbf {HYPE}$
with constant domains. Sequents are understood as pairs of multisets. We work with a language whose logical symbols are
$\mathbf {HYPE}$
with constant domains. Sequents are understood as pairs of multisets. We work with a language whose logical symbols are
![]() $\neg $
,
$\neg $
,
![]() $\vee $
,
$\vee $
,
![]() $\rightarrow $
,
$\rightarrow $
,
![]() $\forall $
,
$\forall $
,
![]() $\bot $
. For
$\bot $
. For
![]() $\Gamma =\gamma _1,\ldots ,\gamma _n$
a multiset
$\Gamma =\gamma _1,\ldots ,\gamma _n$
a multiset
![]() $\neg \Gamma $
is the multiset
$\neg \Gamma $
is the multiset
![]() $\neg \gamma _1,\ldots ,\neg \gamma _n$
. The logical constants
$\neg \gamma _1,\ldots ,\neg \gamma _n$
. The logical constants
![]() $\wedge , \exists ,\leftrightarrow $
can be defined as usual and
$\wedge , \exists ,\leftrightarrow $
can be defined as usual and
![]() $\top $
is defined as
$\top $
is defined as
![]() $\neg \bot $
. Moreover, we can define ‘intuitionistic’ negation
$\neg \bot $
. Moreover, we can define ‘intuitionistic’ negation
![]() $\sim A$
as
$\sim A$
as
![]() $A \rightarrow \bot $
, the material conditional
$A \rightarrow \bot $
, the material conditional
![]() $A\supset B$
as
$A\supset B$
as
![]() $\neg A\vee B$
, and material equivalence
$\neg A\vee B$
, and material equivalence
![]() $A\equiv B$
as
$A\equiv B$
as
![]() $(A\supset B)\land (B\supset A)$
. For A a formula, we write
$(A\supset B)\land (B\supset A)$
. For A a formula, we write
![]() $\texttt {FV}(A)$
for the set of its free variables, and
$\texttt {FV}(A)$
for the set of its free variables, and
![]() $\texttt {FV}(\Gamma )$
for the set of free variables in all formulas in
$\texttt {FV}(\Gamma )$
for the set of free variables in all formulas in
![]() $\Gamma $
.
$\Gamma $
.
The system
![]() $\mathbf {G1h}_{\mathbf {cd}}$
consists of the following initial sequents and rules:
$\mathbf {G1h}_{\mathbf {cd}}$
consists of the following initial sequents and rules:


We write
![]() $\texttt {rk}(A)$
for the logical complexity of A, defined as the number of nodes in the longest branch of its syntactic tree. For a derivation d we let
$\texttt {rk}(A)$
for the logical complexity of A, defined as the number of nodes in the longest branch of its syntactic tree. For a derivation d we let
-
•
 $\texttt {hgt}(d) := \texttt {sup}_{i<n} \{\texttt {hgt} (d_i) + 1\, |\, d_i \text { an immediate subderivation of } d\}$
(the height of the derivation), where
$\texttt {hgt}(d) := \texttt {sup}_{i<n} \{\texttt {hgt} (d_i) + 1\, |\, d_i \text { an immediate subderivation of } d\}$
(the height of the derivation), where
 $d_0, \ldots , d_{n}$
are the immediate subderivations of d.
$d_0, \ldots , d_{n}$
are the immediate subderivations of d.
We say that a formula A is derivable in a system, if the sequent
![]() $\Rightarrow A$
is derivable in it.
$\Rightarrow A$
is derivable in it.
The next lemma collects some basic facts about
![]() $\mathbf {G1h}_{\mathbf {cd}}$
. They mostly concern the admissibility of some basic inferences in
$\mathbf {G1h}_{\mathbf {cd}}$
. They mostly concern the admissibility of some basic inferences in
![]() $\mathbf {G1h}_{\mathbf {cd}}$
.
$\mathbf {G1h}_{\mathbf {cd}}$
.
-
(i) The sequents
 $\Rightarrow \top $
,
$\Rightarrow \top $
,
 $A \Rightarrow \neg \neg A$
,
$A \Rightarrow \neg \neg A$
,
 $\neg \neg A \Rightarrow A$
are derivable in
$\neg \neg A \Rightarrow A$
are derivable in
 $\mathbf {G1h}_{\mathbf {cd}}$
.
$\mathbf {G1h}_{\mathbf {cd}}$
. -
(ii) The rule of contraposition
is admissible in
 $\mathbf {G1h}_{\mathbf {cd}}$
.
$\mathbf {G1h}_{\mathbf {cd}}$
.
-
(iii) The following rules are admissible in
 $\mathbf {G1h}_{\mathbf {cd}}$
:
$\mathbf {G1h}_{\mathbf {cd}}$
:
-
(iv) Intersubstitutivity: If
 $\chi \Rightarrow \chi '$
and
$\chi \Rightarrow \chi '$
and
 $\chi ' \Rightarrow \chi $
, as well as
$\chi ' \Rightarrow \chi $
, as well as
 $\psi $
are derivable in
$\psi $
are derivable in
 $\mathbf {G1h}_{\mathbf {cd}}$
, then
$\mathbf {G1h}_{\mathbf {cd}}$
, then
 $\psi (\chi ' / \chi )$
is derivable, where
$\psi (\chi ' / \chi )$
is derivable, where
 $\psi (\chi ' / \chi )$
is obtained by replacing all occurrences of
$\psi (\chi ' / \chi )$
is obtained by replacing all occurrences of
 $\chi $
in
$\chi $
in
 $\psi $
by
$\psi $
by
 $\chi '$
.
$\chi '$
.
Proof. Claims (i)–(iii) are direct consequences of the contraposition rules (ConCp) and (ClCp). (iv) is proved by a straightforward induction on the height of the derivation in
![]() $\mathbf {G1h}_{\mathbf {cd}}$
.□
$\mathbf {G1h}_{\mathbf {cd}}$
.□
We opted for this specific formulation of
![]() $\mathbf {G1h}_{\mathbf {cd}}$
mainly because it substantially simplifies the presentation of the results of the next sections 3–5, which are the main focus of the paper. From a proof-theoretic point of view, the calculus has some drawbacks even at the propositional level, as the rules ConCp and ClCp compromise the induction needed for cut-elimination. In the propositional case, even if one removes ConCp and ClCp and splits the contraposition rule of Lemma 1(ii) on a case by case manner, problems for cut-elimination remain [Reference Fischer9]. Moreover, when one moves to the quantificational system, there are deeper problems. The same counterexample that is employed to show that cut is not admissible in systems of intuitionistic logic with constant domains can be employed for the systems we are investigating.Footnote
3
Both problems can be addressed by employing techniques from Kashima and Shimura [Reference Kashima and Shimura17], which however rely on the extension of the systems with additional resources.
$\mathbf {G1h}_{\mathbf {cd}}$
mainly because it substantially simplifies the presentation of the results of the next sections 3–5, which are the main focus of the paper. From a proof-theoretic point of view, the calculus has some drawbacks even at the propositional level, as the rules ConCp and ClCp compromise the induction needed for cut-elimination. In the propositional case, even if one removes ConCp and ClCp and splits the contraposition rule of Lemma 1(ii) on a case by case manner, problems for cut-elimination remain [Reference Fischer9]. Moreover, when one moves to the quantificational system, there are deeper problems. The same counterexample that is employed to show that cut is not admissible in systems of intuitionistic logic with constant domains can be employed for the systems we are investigating.Footnote
3
Both problems can be addressed by employing techniques from Kashima and Shimura [Reference Kashima and Shimura17], which however rely on the extension of the systems with additional resources.
Since cut elimination is not the main focus of our paper, we opt for a more compact presentation of
![]() $\mathbf {G1h}_{\mathbf {cd}}$
that fits nicely our purpose of extending it with arithmetic and truth rules.
$\mathbf {G1h}_{\mathbf {cd}}$
that fits nicely our purpose of extending it with arithmetic and truth rules.
2.2 Semantics
In this section we present the semantics of
![]() $\mathbf {G1h}_{\mathbf {cd}}$
(and therefore of
$\mathbf {G1h}_{\mathbf {cd}}$
(and therefore of
![]() $\mathbf {HYPE}$
) and sketch the completeness of
$\mathbf {HYPE}$
) and sketch the completeness of
![]() $\mathbf {G1h}_{\mathbf {cd}}$
. We follow a simplification of the semantics in Leitgeb [Reference Leitgeb19] suggested by Speranski [Reference Speranski25]. Speranski connects
$\mathbf {G1h}_{\mathbf {cd}}$
. We follow a simplification of the semantics in Leitgeb [Reference Leitgeb19] suggested by Speranski [Reference Speranski25]. Speranski connects
![]() $\mathbf {HYPE}$
-models with Routley semantics. A Routley frame
$\mathbf {HYPE}$
-models with Routley semantics. A Routley frame
![]() $\mathfrak {F}$
is a triple
$\mathfrak {F}$
is a triple
![]() $\langle W, \leq , * \rangle $
, where:
$\langle W, \leq , * \rangle $
, where:
-
(i) W is a non-empty set of states;
-
(ii)
 $\leq $
is a preorder;
$\leq $
is a preorder; -
(iii)
 $*$
is a function from W to W, which is:
$*$
is a function from W to W, which is:-
– antimonotone, i.e., for all
 $w,v \in W$
, if
$w,v \in W$
, if
 $w \leq v$
, then
$w \leq v$
, then
 $v^* \leq w^*$
;
$v^* \leq w^*$
; -
– involutive, i.e., for all
 $w \in W$
,
$w \in W$
,
 $w^{**} = w$
.
$w^{**} = w$
.
-
A constant domain model
![]() $\mathfrak {M}$
for
$\mathfrak {M}$
for
![]() $\mathbf {HYPE}$
is a triple
$\mathbf {HYPE}$
is a triple
![]() $(\mathfrak {F}, {D},I)$
where
$(\mathfrak {F}, {D},I)$
where
![]() $\mathfrak {F}$
is a Routley frame,
$\mathfrak {F}$
is a Routley frame,
![]() ${D}$
is a non-empty set (the domain of the model), and I is an interpretation function. In particular, I assigns to every constant c an element of D and it associates with each state w and n-place predicate P a set
${D}$
is a non-empty set (the domain of the model), and I is an interpretation function. In particular, I assigns to every constant c an element of D and it associates with each state w and n-place predicate P a set
![]() $P^{w} \subseteq D^n$
. Constants are interpreted rigidly and, although domains do not grow, we impose the following hereditariness condition: for all
$P^{w} \subseteq D^n$
. Constants are interpreted rigidly and, although domains do not grow, we impose the following hereditariness condition: for all
![]() $v,w \in W$
, if
$v,w \in W$
, if
![]() $v \leq w$
, then for all predicates P,
$v \leq w$
, then for all predicates P,
![]() $P^{v} \subseteq P^{w}$
.
$P^{v} \subseteq P^{w}$
.
Let
![]() $\mathfrak {M}$
be a constant domain model,
$\mathfrak {M}$
be a constant domain model,
![]() $w \in W$
and
$w \in W$
and
![]() $\sigma \colon \text {VAR}\to D$
a variable assignment on D, then the forcing relation
$\sigma \colon \text {VAR}\to D$
a variable assignment on D, then the forcing relation
![]() $\mathfrak {M}, w, \sigma \Vdash A$
is defined inductively:
$\mathfrak {M}, w, \sigma \Vdash A$
is defined inductively:
 $$ \begin{align*} \begin{array}{lc@{\quad}l} \mathfrak{M}, w, \sigma \Vdash P (x_1,\ldots,x_n) & &\text{ iff } (\sigma (x_1),\ldots, \sigma(x_n)) \in P^{w}; \\ \mathfrak{M}, w, \sigma \Vdash \neg A & & \text{ iff } \mathfrak{M}, w^*, \sigma \nVdash A; \\ \mathfrak{M}, w, \sigma \Vdash A \vee B & & \text{ iff } \mathfrak{M}, w, \sigma \Vdash A \text{ or } \mathfrak{M}, w, \sigma{} \Vdash B; \\ \mathfrak{M}, w, \sigma \Vdash A \rightarrow B & & \text{ iff } \text{ for all } v, \text{ with } w \leq v \text{, if } \mathfrak{M}, v, \sigma \Vdash A \text{, then } \mathfrak{M}, v, \sigma \Vdash B; \\ \mathfrak{M}, w, \sigma \Vdash \forall x A & & \text{ iff } \text{ for all } x\text{-variants } \sigma' \text{ of } \sigma, \mathfrak{M}, w, \sigma' \Vdash A; \\ \mathfrak{M}, w, \sigma \nVdash \bot. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lc@{\quad}l} \mathfrak{M}, w, \sigma \Vdash P (x_1,\ldots,x_n) & &\text{ iff } (\sigma (x_1),\ldots, \sigma(x_n)) \in P^{w}; \\ \mathfrak{M}, w, \sigma \Vdash \neg A & & \text{ iff } \mathfrak{M}, w^*, \sigma \nVdash A; \\ \mathfrak{M}, w, \sigma \Vdash A \vee B & & \text{ iff } \mathfrak{M}, w, \sigma \Vdash A \text{ or } \mathfrak{M}, w, \sigma{} \Vdash B; \\ \mathfrak{M}, w, \sigma \Vdash A \rightarrow B & & \text{ iff } \text{ for all } v, \text{ with } w \leq v \text{, if } \mathfrak{M}, v, \sigma \Vdash A \text{, then } \mathfrak{M}, v, \sigma \Vdash B; \\ \mathfrak{M}, w, \sigma \Vdash \forall x A & & \text{ iff } \text{ for all } x\text{-variants } \sigma' \text{ of } \sigma, \mathfrak{M}, w, \sigma' \Vdash A; \\ \mathfrak{M}, w, \sigma \nVdash \bot. \end{array} \end{align*} $$
Finally, we define logical consequence. We write, for
![]() sets of sentences:
sets of sentences:
-
•
 iff: if
iff: if
 $\mathfrak {M},w\Vdash \gamma $
for all
$\mathfrak {M},w\Vdash \gamma $
for all
 $\gamma \in \Gamma $
, then
$\gamma \in \Gamma $
, then
 for some
for some
 ;
; -
•
 iff for all
iff for all
 $\mathfrak {M},w$
:
$\mathfrak {M},w$
:
 .
.
The system
![]() $\mathbf {G1h}_{\mathbf {cd}}$
is equivalent to the Hilbert-style system
$\mathbf {G1h}_{\mathbf {cd}}$
is equivalent to the Hilbert-style system
![]() $\mathbf {QN}^{\circ }$
featuring the axiom schemata
$\mathbf {QN}^{\circ }$
featuring the axiom schemata
 $$ \begin{align*} &A\rightarrow (B\rightarrow A) &&A\rightarrow (B\rightarrow C)\rightarrow ((A\rightarrow B)\rightarrow (A\rightarrow C))\\ &A\land B\rightarrow A && A\land B\rightarrow B\\ &A\rightarrow A\vee B &&B\rightarrow A\vee B\\ &A\rightarrow (B\rightarrow A\land B) && (A\rightarrow C) \rightarrow ((B\rightarrow C)\rightarrow (A\vee B\rightarrow C))\\ & \neg\neg A\rightarrow A && A \rightarrow \neg \neg A\\ &\forall x A \rightarrow A(t)&& A(t)\rightarrow \exists x A \end{align*} $$
$$ \begin{align*} &A\rightarrow (B\rightarrow A) &&A\rightarrow (B\rightarrow C)\rightarrow ((A\rightarrow B)\rightarrow (A\rightarrow C))\\ &A\land B\rightarrow A && A\land B\rightarrow B\\ &A\rightarrow A\vee B &&B\rightarrow A\vee B\\ &A\rightarrow (B\rightarrow A\land B) && (A\rightarrow C) \rightarrow ((B\rightarrow C)\rightarrow (A\vee B\rightarrow C))\\ & \neg\neg A\rightarrow A && A \rightarrow \neg \neg A\\ &\forall x A \rightarrow A(t)&& A(t)\rightarrow \exists x A \end{align*} $$
and the following rules of inference:

![]() $\mathbf {QN}^{\circ }$
is a neater presentation of
$\mathbf {QN}^{\circ }$
is a neater presentation of
![]() $\mathbf {HYPE}$
where a few redundant principles are dropped. The consequences of the two systems are identical.
$\mathbf {HYPE}$
where a few redundant principles are dropped. The consequences of the two systems are identical.
That our system
![]() $\mathbf {G1h}_{\mathbf {cd}}$
is equivalent to
$\mathbf {G1h}_{\mathbf {cd}}$
is equivalent to
![]() $\mathbf {QN}^{\circ }$
can be seen as follows.
$\mathbf {QN}^{\circ }$
can be seen as follows.
![]() $\mathbf {G1h}_{\mathbf {cd}}$
is an extension of intuitionistic logic (modulo the definition of
$\mathbf {G1h}_{\mathbf {cd}}$
is an extension of intuitionistic logic (modulo the definition of
![]() $\sim A$
as
$\sim A$
as
![]() $A\rightarrow \bot )$
. Therefore, since all axioms of
$A\rightarrow \bot )$
. Therefore, since all axioms of
![]() $\mathbf {QN}^{\circ }$
except for the double negation axioms are intuitionistically valid, Lemma 1 enables us to show that all axioms of
$\mathbf {QN}^{\circ }$
except for the double negation axioms are intuitionistically valid, Lemma 1 enables us to show that all axioms of
![]() $\mathbf {QN}^{\circ }$
are consequences of
$\mathbf {QN}^{\circ }$
are consequences of
![]() $\mathbf {G1h}_{\mathbf {cd}}$
. Additionally, Lemma 1 shows that contraposition is admissible in
$\mathbf {G1h}_{\mathbf {cd}}$
. Additionally, Lemma 1 shows that contraposition is admissible in
![]() $\mathbf {G1h}_{\mathbf {cd}}$
. Rules for quantifiers are easily established in
$\mathbf {G1h}_{\mathbf {cd}}$
. Rules for quantifiers are easily established in
![]() $\mathbf {G1h}_{\mathbf {cd}}$
. For the other direction a proof on the length of the derivation is sufficient. The fact that the deduction theorem holds in
$\mathbf {G1h}_{\mathbf {cd}}$
. For the other direction a proof on the length of the derivation is sufficient. The fact that the deduction theorem holds in
![]() $\mathbf {QN}^{\circ }$
renders the proof particularly simple. Therefore, we have:
$\mathbf {QN}^{\circ }$
renders the proof particularly simple. Therefore, we have:
Lemma 2.
![]() iff
iff
![]() .
.
Lemma 2 then entails that
![]() $\mathbf {G1h}_{\mathbf {cd}}$
is equivalent to Leitgeb’s
$\mathbf {G1h}_{\mathbf {cd}}$
is equivalent to Leitgeb’s
![]() $\mathbf {HYPE}$
.
$\mathbf {HYPE}$
.
Speranski [Reference Speranski25] establishes a strong completeness result (for countable signatures) for
![]() $\mathbf {QN}^{\circ }$
.Footnote
4
Speranski uses a Henkin-style proof similar to the strategy employed in Gabbay et al. [Reference Gabbay, Shehtman and Skvortsov11, sec. 7.2] for intuitionistic logic with constant domains. Leitgeb [Reference Leitgeb19] establishes a (weak) completeness proof for his Hilbert style system based on the work of Görnemann [Reference Görnemann12]. By Lemma 2 we can employ Speranski’s completeness result for our system
$\mathbf {QN}^{\circ }$
.Footnote
4
Speranski uses a Henkin-style proof similar to the strategy employed in Gabbay et al. [Reference Gabbay, Shehtman and Skvortsov11, sec. 7.2] for intuitionistic logic with constant domains. Leitgeb [Reference Leitgeb19] establishes a (weak) completeness proof for his Hilbert style system based on the work of Görnemann [Reference Görnemann12]. By Lemma 2 we can employ Speranski’s completeness result for our system
![]() $\mathbf {G1h}_{\mathbf {cd}}$
with respect to Routley semantics:
$\mathbf {G1h}_{\mathbf {cd}}$
with respect to Routley semantics:
Proposition 1 (Completeness of G 1 h cd [Reference Speranski25])
![]() iff there is a finite
iff there is a finite
![]() , such that
, such that
![]() .
.
We now turn to investigating how much classical reasoning can be reproduced in our logic. Such questions will turn out to be essential components of the analysis of truth theories over
![]() $\mathbf {HYPE}$
.
$\mathbf {HYPE}$
.
2.3 HYPE and recapture
One of the desirable properties of the nonclassical logics employed in the debate on semantic paradoxes is the capability of recapturing classical reasoning in domains where there is no risk of paradoxicality, such as mathematics [Reference Field7, chap. 4].Footnote 5
The following lemma summarizes the recapture properties of
![]() $\mathbf {G1h}_{\mathbf {cd}}$
and extensions thereof. It essentially states that, in systems based on
$\mathbf {G1h}_{\mathbf {cd}}$
and extensions thereof. It essentially states that, in systems based on
![]() $\mathbf {G1h}_{\mathbf {cd}}$
, once we restrict our attention to a fragment of the language satisfying the excluded middle and/or explosion, the native HYPE-negation and conditional, as well as the defined intuitionistic negation, all behave classically.
$\mathbf {G1h}_{\mathbf {cd}}$
, once we restrict our attention to a fragment of the language satisfying the excluded middle and/or explosion, the native HYPE-negation and conditional, as well as the defined intuitionistic negation, all behave classically.
-
(i) The following rules are admissible in extensions of
 $\mathbf {G1h}_{\mathbf {cd}}$
:
$\mathbf {G1h}_{\mathbf {cd}}$
:
-
(ii) The previous fact can be used to show, by an induction on
 $\texttt {rk}(A)$
, that
$\texttt {rk}(A)$
, that
 $\Rightarrow A,\neg A$
is derivable for any formula whenever
$\Rightarrow A,\neg A$
is derivable for any formula whenever
 $\Rightarrow P,\neg P$
is derivable for any atomic P in A.
$\Rightarrow P,\neg P$
is derivable for any atomic P in A.
Proof. We prove the claims for the crucial cases in which a conditional is involved:
For (i):

For (ii):

□
Remark 1. The induction involved in Lemma 3(ii) does not go through in intuitionistic logic with the
![]() $\mathbf {HYPE}$
-negation
$\mathbf {HYPE}$
-negation
![]() $\neg $
replaced by the intuitionistic negation
$\neg $
replaced by the intuitionistic negation
![]() $\sim $
.
$\sim $
.
2.4 Equality
For our purposes it’s important to extend
![]() $\mathbf {G1h}_{\mathbf {cd}}$
with a theory of equality.
$\mathbf {G1h}_{\mathbf {cd}}$
with a theory of equality.
![]() $\mathbf {G1h_{cd}^=}$
is obtained by adding to
$\mathbf {G1h_{cd}^=}$
is obtained by adding to
![]() $\mathbf {G1h}_{\mathbf {cd}}$
the following initial sequents for equality.
$\mathbf {G1h}_{\mathbf {cd}}$
the following initial sequents for equality.
By an essential use of
![]() $\texttt {ConCp}$
, we can establish in
$\texttt {ConCp}$
, we can establish in
![]() $\mathbf {G1h_{cd}^=}$
that identity statements behave classically.
$\mathbf {G1h_{cd}^=}$
that identity statements behave classically.
Lemma 4.
![]() $\mathbf {G1h_{cd}^=}$
derives
$\mathbf {G1h_{cd}^=}$
derives
![]() $\Rightarrow s = t, \neg s = t$
and
$\Rightarrow s = t, \neg s = t$
and
![]() $s = t, \neg s = t \Rightarrow $
.
$s = t, \neg s = t \Rightarrow $
.
Proof. We use the identity sequents:

□
Lemma 4 reveals some subtle issues concerning the treatment of identity in subclassical logics generally employed to deal with semantical paradoxes. It tells us that identity is essentially treated as a classical notion in
![]() $\mathbf {G1h}_{\mathbf {cd}}^{=}$
. To obtain a similar phenomenon in absence of
$\mathbf {G1h}_{\mathbf {cd}}^{=}$
. To obtain a similar phenomenon in absence of
![]() $\texttt {ConCp}$
and
$\texttt {ConCp}$
and
![]() $\texttt {ClCp}$
, one would have to add the counterpositives of
$\texttt {ClCp}$
, one would have to add the counterpositives of
![]() $\texttt {Rep}$
and
$\texttt {Rep}$
and
![]() $\texttt {Ref}$
to the system. A nonclassical treatment of identity would require some non-trivial changes to
$\texttt {Ref}$
to the system. A nonclassical treatment of identity would require some non-trivial changes to
![]() $\texttt {Rep}$
and
$\texttt {Rep}$
and
![]() $\texttt {Ref}$
. That identity is a classical notion is perfectly in line with our framework, in which identity is a non-semantic notion akin to mathematical notions.
$\texttt {Ref}$
. That identity is a classical notion is perfectly in line with our framework, in which identity is a non-semantic notion akin to mathematical notions.
3 Arithmetic in HYPE
Starting with the logical constants introduced above and the identity symbol, we now work with a suitable expansion of the usual signature
![]() $\{0,\texttt {S},+,\times \}$
by finitely many function symbols for selected primitive recursive functions. Such function symbols are needed for a smooth representation of formal syntax. We call this language
$\{0,\texttt {S},+,\times \}$
by finitely many function symbols for selected primitive recursive functions. Such function symbols are needed for a smooth representation of formal syntax. We call this language
![]() $\mathcal {L}_{\mathbb {N}}^{\rightarrow }$
. We will also make use of the
$\mathcal {L}_{\mathbb {N}}^{\rightarrow }$
. We will also make use of the
![]() $\rightarrow $
-free fragment of the language of arithmetic, which we label as
$\rightarrow $
-free fragment of the language of arithmetic, which we label as
![]() $\mathcal {L}_{\mathbb {N}}$
. Our base theory will then be obtained by extending the logic
$\mathcal {L}_{\mathbb {N}}$
. Our base theory will then be obtained by extending the logic
![]() $\mathbf {G1h_{cd}^=}$
with the basic axioms for
$\mathbf {G1h_{cd}^=}$
with the basic axioms for
![]() $0,\texttt {S},+,\times $
(axioms
$0,\texttt {S},+,\times $
(axioms
![]() $\mathbf {Q}1$
–
$\mathbf {Q}1$
–
![]() $2$
,
$2$
,
![]() $\mathbf {Q}4$
–
$\mathbf {Q}4$
–
![]() $7$
of [Reference Hájek and Pudlák13]), and the recursive clauses for these additional function symbols. The resulting system will be called
$7$
of [Reference Hájek and Pudlák13]), and the recursive clauses for these additional function symbols. The resulting system will be called
![]() $\mathbf {HYA}^-$
.
$\mathbf {HYA}^-$
.
In the following, the role of rule and axiom schemata will be crucial. It will be particularly important to keep track of the classes of instances of a particular schema, and therefore we will always relativize schemata to specific languages and understand the schema as the set of all its instances in that language. For example, in the case of the induction axioms we use the label
![]() $\texttt {IND}^{\rightarrow } (\mathcal {L})$
to refer to the set of all sequents of the form
$\texttt {IND}^{\rightarrow } (\mathcal {L})$
to refer to the set of all sequents of the form
where A is a formula of
![]() $\mathcal {L}$
. Similarly, induction rules
$\mathcal {L}$
. Similarly, induction rules
![]() $\texttt {IND}^{\texttt {R}}(\mathcal {L})$
will refer to all rule instances
$\texttt {IND}^{\texttt {R}}(\mathcal {L})$
will refer to all rule instances

for A a formula of
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
We call
![]() $\mathbf {HYA}$
the extension of
$\mathbf {HYA}$
the extension of
![]() $\mathbf {HYA}^-$
by the induction axiom
$\mathbf {HYA}^-$
by the induction axiom
![]() $\texttt {IND}^{\rightarrow }(\mathcal {L})$
.
$\texttt {IND}^{\rightarrow }(\mathcal {L})$
.
![]() $\mathbf {HYA}$
is equivalent to Peano Arithmetic
$\mathbf {HYA}$
is equivalent to Peano Arithmetic
![]() $\mathbf {PA}$
. This is essentially because of the recapture properties of our logic. For formulas A containing only classical vocabulary, the properties stated in Lemma 3 entail that the rule and sequent formulations of induction are equivalent.
$\mathbf {PA}$
. This is essentially because of the recapture properties of our logic. For formulas A containing only classical vocabulary, the properties stated in Lemma 3 entail that the rule and sequent formulations of induction are equivalent.
Lemma 5. Let
![]() $\mathcal {L}\supseteq \mathcal {L}_{\mathbb {N}}^{\rightarrow }$
. Over
$\mathcal {L}\supseteq \mathcal {L}_{\mathbb {N}}^{\rightarrow }$
. Over
![]() $\mathbf {HYA}^-: \texttt {IND}^{\texttt {R}}(\mathcal {L})$
and
$\mathbf {HYA}^-: \texttt {IND}^{\texttt {R}}(\mathcal {L})$
and
![]() $\texttt {IND}^{\rightarrow }(\mathcal {L})$
are equivalent when restricted to formulas A such that
$\texttt {IND}^{\rightarrow }(\mathcal {L})$
are equivalent when restricted to formulas A such that
![]() $\Rightarrow A, \neg A$
.
$\Rightarrow A, \neg A$
.
Since for
![]() $A \in \mathcal {L}_{\mathbb {N}}^{\rightarrow }$
,
$A \in \mathcal {L}_{\mathbb {N}}^{\rightarrow }$
,
![]() $\Rightarrow A, \neg A$
and
$\Rightarrow A, \neg A$
and
![]() $A, \neg A \Rightarrow $
are derivable in
$A, \neg A \Rightarrow $
are derivable in
![]() $\mathbf {G1h_{cd}}$
, we have the immediate corollary that:
$\mathbf {G1h_{cd}}$
, we have the immediate corollary that:
Corollary 1.
![]() $\mathbf {HYA}$
and
$\mathbf {HYA}$
and
![]() $\mathbf {PA}$
are identical theories.
$\mathbf {PA}$
are identical theories.
Corollary 1 tells us that, in the absence of non-arithmetical predicates, such as the truth predicate, the conditional of HYPE collapses into the material conditional. It is only in the presence of semantical predicates interacting with the conditional that allows for full proof-theoretic strength of classical reasoning.
It is important to highlight that
![]() $\mathbf {HYA}$
is the base theory for our theory of truth, which is not the same as the object-theory for which our theory of truth is formulated.
$\mathbf {HYA}$
is the base theory for our theory of truth, which is not the same as the object-theory for which our theory of truth is formulated.
![]() $\mathbf {HYA}$
contains already some tools that will be essential for the formulation of the theory of truth, such as induction principles extended with the conditional of HYPE.
$\mathbf {HYA}$
contains already some tools that will be essential for the formulation of the theory of truth, such as induction principles extended with the conditional of HYPE.
3.1 Ordinals and transfinite induction
Our notational conventions for schemata generalize to schemata other than induction. A prominent role in the paper will be played by transfinite induction schemata. In order to introduce them, we need to assume a notation system
![]() $(\texttt {OT},\prec )$
for ordinals up to the Feferman–Schütte ordinal
$(\texttt {OT},\prec )$
for ordinals up to the Feferman–Schütte ordinal
![]() $\Gamma _0$
as it can be found, for instance, in [Reference Pohlers23, chap. 2].
$\Gamma _0$
as it can be found, for instance, in [Reference Pohlers23, chap. 2].
![]() $\texttt {OT}$
is a primitive recursive set of ordinal codes and
$\texttt {OT}$
is a primitive recursive set of ordinal codes and
![]() $\prec $
a primitive recursive relation on
$\prec $
a primitive recursive relation on
![]() $\texttt {OT}$
that is isomorphic to the usual ordering of ordinals up to
$\texttt {OT}$
that is isomorphic to the usual ordering of ordinals up to
![]() $\Gamma _0$
. We distinguish between fixed ordinal codes, which we denote with
$\Gamma _0$
. We distinguish between fixed ordinal codes, which we denote with
![]() $\alpha ,\beta ,\gamma ,\ldots $
, and
$\alpha ,\beta ,\gamma ,\ldots $
, and
![]() $\zeta ,\eta ,\theta ,\xi ,\ldots $
as abbreviations for variables ranging over elements of OT. Our representation of ordinals satisfies all standard properties. In particular, we will make implicit use of the properties listed in [Reference Troelstra and Schwichtenberg28, p. 322].
$\zeta ,\eta ,\theta ,\xi ,\ldots $
as abbreviations for variables ranging over elements of OT. Our representation of ordinals satisfies all standard properties. In particular, we will make implicit use of the properties listed in [Reference Troelstra and Schwichtenberg28, p. 322].
We will make extensive use of the following abbreviations. We call a formula progressive if it is preserved upward by the ordinals:
where
![]() $\forall \zeta \prec \eta \, A(\zeta )$
is short for
$\forall \zeta \prec \eta \, A(\zeta )$
is short for
![]() $\forall \zeta (\zeta \prec \eta \rightarrow A(\zeta ))$
. We will use this (standard) notational convention in several occasions in what follows. Similarly, we will write
$\forall \zeta (\zeta \prec \eta \rightarrow A(\zeta ))$
. We will use this (standard) notational convention in several occasions in what follows. Similarly, we will write
![]() $\exists \zeta \prec \eta \, A(\zeta )$
for
$\exists \zeta \prec \eta \, A(\zeta )$
for
![]() $\exists \zeta (\zeta \prec \eta \land A(\zeta ))$
.
$\exists \zeta (\zeta \prec \eta \land A(\zeta ))$
.
This formulation of progressiveness is
![]() $\mathbf {HYA}$
-equivalent to a formulation as a sequent
$\mathbf {HYA}$
-equivalent to a formulation as a sequent
![]() $\forall \zeta \prec \eta \, A(\zeta ) \Rightarrow A (\eta )$
. Moreover, if
$\forall \zeta \prec \eta \, A(\zeta ) \Rightarrow A (\eta )$
. Moreover, if
![]() $A(x)\vee \neg A(x)$
is provable, then
$A(x)\vee \neg A(x)$
is provable, then
![]() $\texttt {Prog}(A)$
is
$\texttt {Prog}(A)$
is
![]() $\mathbf {HYA}$
-equivalent to:
$\mathbf {HYA}$
-equivalent to:
Transfinite induction up to the ordinal
![]() $\alpha \; (\prec \Gamma _0)$
will be formulated as the following sequent:
$\alpha \; (\prec \Gamma _0)$
will be formulated as the following sequent:
An alternative would be to use a rule-formulation:

![]() $\texttt {TI}_{\alpha }^{\texttt {r}}(A)$
differs from the standard rule formulation of transfinite induction (see, e.g., [Reference Halbach14]) in that its premise features only one formula in the succedent: this is because of the intuitionistic nature of the
$\texttt {TI}_{\alpha }^{\texttt {r}}(A)$
differs from the standard rule formulation of transfinite induction (see, e.g., [Reference Halbach14]) in that its premise features only one formula in the succedent: this is because of the intuitionistic nature of the
![]() $\mathbf {HYPE}$
-conditional that is apparent in the rule
$\mathbf {HYPE}$
-conditional that is apparent in the rule
![]() $(\texttt {R}\!\rightarrow )$
.
$(\texttt {R}\!\rightarrow )$
.
The two formulations of induction just introduced are equivalent over
![]() $\mathbf {HYA}^-$
, i.e., given
$\mathbf {HYA}^-$
, i.e., given
![]() $\texttt {TI}_{\alpha }(A)$
,
$\texttt {TI}_{\alpha }(A)$
,
![]() $\texttt {TI}_{\alpha }^{\texttt {r}}(A)$
is admissible, and given
$\texttt {TI}_{\alpha }^{\texttt {r}}(A)$
is admissible, and given
![]() $\texttt {TI}_{\alpha }^{\texttt {r}}(A)$
,
$\texttt {TI}_{\alpha }^{\texttt {r}}(A)$
,
![]() $\texttt {TI}_{\alpha }(A)$
is derivable.Footnote
6
$\texttt {TI}_{\alpha }(A)$
is derivable.Footnote
6
![]() $\texttt {TI}_{\alpha }(\mathcal {L})$
is short for
$\texttt {TI}_{\alpha }(\mathcal {L})$
is short for
![]() $\texttt {TI}_{\alpha } (A)$
for every formula A of the language
$\texttt {TI}_{\alpha } (A)$
for every formula A of the language
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
![]() $\texttt {TI}_{< \alpha } (\mathcal {L})$
is short for
$\texttt {TI}_{< \alpha } (\mathcal {L})$
is short for
![]() $\texttt {TI}_{\beta } (\mathcal {L})$
for all
$\texttt {TI}_{\beta } (\mathcal {L})$
for all
![]() $\beta \prec \alpha $
. The function
$\beta \prec \alpha $
. The function
![]() $\omega _n$
is recursively defined in the standard way as:
$\omega _n$
is recursively defined in the standard way as:
![]() $\omega _0=1$
,
$\omega _0=1$
,
![]() $\omega _{n+1}=\omega ^{\omega _n}$
.
$\omega _{n+1}=\omega ^{\omega _n}$
.
3.2 Transfinite induction and nonclassical predicates
Our main purpose in this paper is to study the proof-theoretic properties of extensions of
![]() $\mathbf {HYA}$
with additional predicates that may not behave classically—i.e., they may not satisfy Lemma 5. In fact, in the case of the pure arithmetical language, Lemma 5 gives us immediately that
$\mathbf {HYA}$
with additional predicates that may not behave classically—i.e., they may not satisfy Lemma 5. In fact, in the case of the pure arithmetical language, Lemma 5 gives us immediately that
![]() $\mathbf {HYA}$
derives
$\mathbf {HYA}$
derives
![]() $\texttt {TI}_{< \varepsilon _0} ( \mathcal {L}_{\mathbb {N}}^{\rightarrow } )$
. In this section we show directly that Gentzen’s original proof of
$\texttt {TI}_{< \varepsilon _0} ( \mathcal {L}_{\mathbb {N}}^{\rightarrow } )$
. In this section we show directly that Gentzen’s original proof of
![]() $\texttt {TI}_{< \varepsilon _0} ( \mathcal {L}_{\mathbb {N}}^{\rightarrow } )$
can be carried out in
$\texttt {TI}_{< \varepsilon _0} ( \mathcal {L}_{\mathbb {N}}^{\rightarrow } )$
can be carried out in
![]() $\mathbf {HYA}$
for suitable expansions of
$\mathbf {HYA}$
for suitable expansions of
![]() $\mathcal {L}_{\mathbb {N}}^{\rightarrow }$
.Footnote
7
To abuse slightly of notation, we will keep the label HYA for the versions of HYA formulated in languages with additional predicate symbols.
$\mathcal {L}_{\mathbb {N}}^{\rightarrow }$
.Footnote
7
To abuse slightly of notation, we will keep the label HYA for the versions of HYA formulated in languages with additional predicate symbols.
Theorem 1. Let
![]() $\mathcal {L}^+$
be a language expansion of
$\mathcal {L}^+$
be a language expansion of
![]() $\mathcal {L}_{\mathbb {N}}^{\rightarrow }$
by finitely many predicate symbols. Then
$\mathcal {L}_{\mathbb {N}}^{\rightarrow }$
by finitely many predicate symbols. Then
![]() $\mathbf {HYA} \vdash \texttt {TI}_{< \varepsilon _0} (\mathcal {L}^+)$
.
$\mathbf {HYA} \vdash \texttt {TI}_{< \varepsilon _0} (\mathcal {L}^+)$
.
The rest of this subsection will be devoted to the proof of Theorem 1, which will involve several preliminary lemmata.
A key ingredient of Gentzen’s proof—which will also play an important role in sections 4 and 5—is Gentzen’s jump formula:
Lemma 6. For any
![]() $A\in \mathcal {L}^+$
,
$A\in \mathcal {L}^+$
,
![]() $\mathbf {HYA}$
proves
$\mathbf {HYA}$
proves
![]() $\texttt {Prog} (A) \Rightarrow \texttt {Prog}(A^+)$
.
$\texttt {Prog} (A) \Rightarrow \texttt {Prog}(A^+)$
.
Proof. The argument is as follows: We assume
![]() $\texttt {Prog}(A)$
and we want to show
$\texttt {Prog}(A)$
and we want to show
![]() $\texttt {Prog}(A^+)$
, i.e.,
$\texttt {Prog}(A^+)$
, i.e.,
![]() $\forall \zeta \prec \theta \, A^+ (\zeta ) \rightarrow A^+ (\theta )$
. So we also assume
$\forall \zeta \prec \theta \, A^+ (\zeta ) \rightarrow A^+ (\theta )$
. So we also assume
![]() $\forall \zeta \prec \theta \, A^+ (\zeta )$
and
$\forall \zeta \prec \theta \, A^+ (\zeta )$
and
![]() $\forall \zeta (\zeta \prec \xi \rightarrow A(\zeta ))$
and
$\forall \zeta (\zeta \prec \xi \rightarrow A(\zeta ))$
and
![]() $\eta \prec \xi + \omega ^{\theta }$
to show
$\eta \prec \xi + \omega ^{\theta }$
to show
![]() $A(\eta )$
.
$A(\eta )$
.
Informally, we make a case distinction: Either
![]() $\theta = 0$
or
$\theta = 0$
or
![]() $\theta \succ 0$
.
$\theta \succ 0$
.
Case 1: If
![]() $\theta = 0$
, then
$\theta = 0$
, then
We have, by the reflexivity sequents and logical rules:
Again by reflexivity and the identity axioms:
By (2)–(4) and (Cut), we obtain
Case 2:
![]() $\theta \succ 0$
. Then by a derivable version of Cantor’s Normal Form Theorem:
$\theta \succ 0$
. Then by a derivable version of Cantor’s Normal Form Theorem:
Given that induction for ordinal notations up to
![]() $\omega $
is provable in
$\omega $
is provable in
![]() $\mathbf {HYA}$
, we will show by induction on
$\mathbf {HYA}$
, we will show by induction on
![]() $n\prec \omega $
that
$n\prec \omega $
that
The base case is straightforward because the following is trivially derivable (by property (ord6) in [Reference Troelstra and Schwichtenberg28, p. 322]):
For the induction step, we start by noticing that by instantiating
![]() $\xi $
in
$\xi $
in
![]() $A^+(\theta _0)$
with
$A^+(\theta _0)$
with
![]() $\xi +\omega ^{\theta _0}\cdot n$
, we obtain
$\xi +\omega ^{\theta _0}\cdot n$
, we obtain
As mentioned, by letting
![]() $\textbf {HYA}$
proves the
$\textbf {HYA}$
proves the
![]() $\omega $
-induction principle (with
$\omega $
-induction principle (with
![]() $n\prec \omega $
)
$n\prec \omega $
)
Therefore, by a series of cuts, we obtain
From (8) we obtain
Therefore, we can instantiate n and
![]() $\zeta $
(with
$\zeta $
(with
![]() $\eta $
), and move the antecedent of
$\eta $
), and move the antecedent of
![]() $\eta \prec \xi + \omega ^{\theta _0} \cdot n \rightarrow A (\eta )$
from the right-hand side to the left hand side of the sequent arrow. Since both n and
$\eta \prec \xi + \omega ^{\theta _0} \cdot n \rightarrow A (\eta )$
from the right-hand side to the left hand side of the sequent arrow. Since both n and
![]() $\eta $
are general, we can existentially generalize over them to get
$\eta $
are general, we can existentially generalize over them to get
which in turn by
![]() gives us
gives us
Now we combine the two cases. Together with our (5) in Case 1, the last sequent enables us to derive
By the provability of
![]() $\theta = 0 \vee \theta \succ 0$
and applications of the rules
$\theta = 0 \vee \theta \succ 0$
and applications of the rules
![]() $(\texttt {R} \rightarrow )$
and
$(\texttt {R} \rightarrow )$
and
![]() $(\texttt {R} \forall )$
we finally get
$(\texttt {R} \forall )$
we finally get
□
The progressiveness of Gentzen’s jump formula enables us then to establish:
Lemma 7. If
![]() $\texttt {TI}_{\alpha } (\mathcal {L}^+)$
is derivable in
$\texttt {TI}_{\alpha } (\mathcal {L}^+)$
is derivable in
![]() $\textbf {HYA}$
, then
$\textbf {HYA}$
, then
![]() ${ \texttt {TI}}_{\omega ^{\alpha }}({\mathcal L}^+)$
is derivable in
${ \texttt {TI}}_{\omega ^{\alpha }}({\mathcal L}^+)$
is derivable in
![]() $\bf {HYA}$
.
$\bf {HYA}$
.
Proof. We assume
![]() $\texttt {TI}_{\alpha } (\mathcal {L}^+)$
. Specifically we have
$\texttt {TI}_{\alpha } (\mathcal {L}^+)$
. Specifically we have
By the meaning of
![]() $\texttt {Prog}(A^+)$
, we obtain
$\texttt {Prog}(A^+)$
, we obtain
By the previous Lemma 6 and cut we also have
which is
But also
and therefore by (15) taking
![]() $\xi = 0$
, we obtain
$\xi = 0$
, we obtain
as desired.□
Corollary 2. If A is such that
![]() $\mathbf {HYA}$
proves
$\mathbf {HYA}$
proves
![]() $A(x)\vee \neg A(x)$
, we have that, if
$A(x)\vee \neg A(x)$
, we have that, if
![]() $\mathbf {HYA}$
proves the classical transfinite induction axiom schema for
$\mathbf {HYA}$
proves the classical transfinite induction axiom schema for
![]() $\alpha $
$\alpha $
then
![]() $\mathbf {HYA}$
proves
$\mathbf {HYA}$
proves
By Lemmas 3(ii) and 4,
![]() $\mathbf {HYA}$
proves
$\mathbf {HYA}$
proves
![]() $A(x)\vee \neg A(x)$
for any formula
$A(x)\vee \neg A(x)$
for any formula
![]() $A(x)$
of
$A(x)$
of
![]() $\mathcal {L}_{\mathbb {N}}$
. Therefore, Corollary 2 entails the proof above can be carried out by replacing the
$\mathcal {L}_{\mathbb {N}}$
. Therefore, Corollary 2 entails the proof above can be carried out by replacing the
![]() $\mathbf {HYPE}$
-conditional with the material conditional when arithmetical properties are at stake.
$\mathbf {HYPE}$
-conditional with the material conditional when arithmetical properties are at stake.
All is set up to finally prove the main result of this section, the admissibility in
![]() $\mathbf {HYA}$
of the required schema of transfinite induction up to any ordinal
$\mathbf {HYA}$
of the required schema of transfinite induction up to any ordinal
![]() $\alpha \prec \varepsilon _0$
.
$\alpha \prec \varepsilon _0$
.
Proof of Theorem 1
The result follows immediately from Lemma 7. Since
![]() $\texttt {TI}_{\omega _0}(A)$
is trivially derivable in
$\texttt {TI}_{\omega _0}(A)$
is trivially derivable in
![]() $\mathbf {HYA}$
, the lemma tells us that
$\mathbf {HYA}$
, the lemma tells us that
![]() $\texttt {TI}_{\omega _n}(A)$
, for each n, can be reached in finitely many proof steps.
$\texttt {TI}_{\omega _n}(A)$
, for each n, can be reached in finitely many proof steps.
Theorem 1 is key to our proof-theoretic analysis of a theory of truth over
![]() $\mathbf {HYPE}$
. We now turn to the definition of such a truth theory.
$\mathbf {HYPE}$
. We now turn to the definition of such a truth theory.
4 The theory of truth
 ${\textbf {KFL}}$
${\textbf {KFL}}$
In this section we introduce the theory of truth
![]() ${\textbf {KFL}}$
, standing for Kripke–Feferman–Leitgeb. The theory is formulated in the language
${\textbf {KFL}}$
, standing for Kripke–Feferman–Leitgeb. The theory is formulated in the language
![]() $\mathcal L_{\texttt {Tr}}^{\rightarrow }:=\mathcal {L}_{\mathbb {N}}^{\rightarrow } \cup \{\texttt {Tr}\}$
, where
$\mathcal L_{\texttt {Tr}}^{\rightarrow }:=\mathcal {L}_{\mathbb {N}}^{\rightarrow } \cup \{\texttt {Tr}\}$
, where
![]() $\texttt {Tr}$
is a unary predicate for truth.
$\texttt {Tr}$
is a unary predicate for truth.
![]() ${\textbf {KFL}}$
is a theory of truth for a
${\textbf {KFL}}$
is a theory of truth for a
![]() $\rightarrow $
-free language
$\rightarrow $
-free language
![]() $\mathcal L_{\texttt {Tr}}$
, which is simply the
$\mathcal L_{\texttt {Tr}}$
, which is simply the
![]() $\rightarrow $
-free fragment of
$\rightarrow $
-free fragment of
![]() $\mathcal L_{\texttt {Tr}}^{\rightarrow }$
. Semantically (cf. Section 4.1), the conditional amounts to a device to navigate between fixed-point models of
$\mathcal L_{\texttt {Tr}}^{\rightarrow }$
. Semantically (cf. Section 4.1), the conditional amounts to a device to navigate between fixed-point models of
![]() $\mathcal L_{\texttt {Tr}}$
in the sense of [Reference Kripke18]. The basic idea is that, given different interpretations of the truth predicate corresponding to different fixed-point models, the conditional enables us to evaluate hypothetical claims involving truth ascriptions that belong to ‘non-actual’ extensions. In other words, in evaluating a conditional
$\mathcal L_{\texttt {Tr}}$
in the sense of [Reference Kripke18]. The basic idea is that, given different interpretations of the truth predicate corresponding to different fixed-point models, the conditional enables us to evaluate hypothetical claims involving truth ascriptions that belong to ‘non-actual’ extensions. In other words, in evaluating a conditional
![]() $A \rightarrow B$
at a state (fixed point) s, we are in fact analyzing whether the satisfaction of A in expansions
$A \rightarrow B$
at a state (fixed point) s, we are in fact analyzing whether the satisfaction of A in expansions
![]() $s'$
of the extension of the truth predicate at s implies the satisfaction of B at
$s'$
of the extension of the truth predicate at s implies the satisfaction of B at
![]() $s'$
. For instance, if our structure of fixed points comprises the minimal and maximal fixed points only, the conditional
$s'$
. For instance, if our structure of fixed points comprises the minimal and maximal fixed points only, the conditional
![]() $\tau \rightarrow \texttt {Tr}\ulcorner \tau \urcorner $
—with
$\tau \rightarrow \texttt {Tr}\ulcorner \tau \urcorner $
—with
![]() $\tau $
a truth-teller sentence—will be satisfied at the minimal fixed point because of the properties of the other fixed point. We elaborate further on the role of the conditional in Section 6. However, we would like to stress that the specific semantic interpretation of the conditional is not our primary concern in this work, but we are mainly concerned with its proof-theoretic properties.
$\tau $
a truth-teller sentence—will be satisfied at the minimal fixed point because of the properties of the other fixed point. We elaborate further on the role of the conditional in Section 6. However, we would like to stress that the specific semantic interpretation of the conditional is not our primary concern in this work, but we are mainly concerned with its proof-theoretic properties.
Definition 1 (The language
 $\mathcal L_{\texttt {Tr}}$
)
$\mathcal L_{\texttt {Tr}}$
)
The logical symbols of
![]() $\mathcal L_{\texttt {Tr}}$
are
$\mathcal L_{\texttt {Tr}}$
are
![]() $\bot , \neg ,\vee ,\forall $
. In addition, we have the identity symbol
$\bot , \neg ,\vee ,\forall $
. In addition, we have the identity symbol
![]() $=$
. Its non-logical vocabulary amounts to the arithmetical vocabulary of
$=$
. Its non-logical vocabulary amounts to the arithmetical vocabulary of
![]() $\mathcal {L}_{\mathbb {N}}$
and the truth predicate
$\mathcal {L}_{\mathbb {N}}$
and the truth predicate
![]() $\texttt {Tr}$
.
$\texttt {Tr}$
.
We assume a canonical representation of the syntax of
![]() $\mathcal L_{\texttt {Tr}}$
in
$\mathcal L_{\texttt {Tr}}$
in
![]() $\mathbf {HYA}$
. Given the equivalence of
$\mathbf {HYA}$
. Given the equivalence of
![]() $\mathbf {HYA}$
and
$\mathbf {HYA}$
and
![]() $\mathbf {PA}$
for arithmetical vocabulary stated in Corollary 1, we can assume one of the standard ways of achieving this (e.g., [Reference Cantini1]). We apply most of the notational conventions—e.g., Feferman’s dot notation—described in [Reference Halbach14, sec. I.5].
$\mathbf {PA}$
for arithmetical vocabulary stated in Corollary 1, we can assume one of the standard ways of achieving this (e.g., [Reference Cantini1]). We apply most of the notational conventions—e.g., Feferman’s dot notation—described in [Reference Halbach14, sec. I.5].
Definition 2 (The theory KFL)
![]() ${\textbf {KFL}}$
extends
${\textbf {KFL}}$
extends
![]() $\mathbf {HYA}$
formulated in
$\mathbf {HYA}$
formulated in
![]() $\mathcal L_{\texttt {Tr}}^ \rightarrow $
—i.e., with the induction schema extended to
$\mathcal L_{\texttt {Tr}}^ \rightarrow $
—i.e., with the induction schema extended to
![]() $\mathcal L_{\texttt {Tr}}^{\rightarrow }$
—with the following truth initial sequents:
$\mathcal L_{\texttt {Tr}}^{\rightarrow }$
—with the following truth initial sequents:

In
![]() ${\textbf {KFL}}$
5,
${\textbf {KFL}}$
5,
![]() $x(y/v)$
denotes the result of substituting, in the formula with code x, the variable with code v with the closed term coded by y. In particular, in
$x(y/v)$
denotes the result of substituting, in the formula with code x, the variable with code v with the closed term coded by y. In particular, in
![]() ${\textbf {KFL}}$
2,
${\textbf {KFL}}$
2,
![]() stands for the result of substituting, in the code of
stands for the result of substituting, in the code of
![]() $\texttt {Tr} v$
, the variable v with the numeral for x.
$\texttt {Tr} v$
, the variable v with the numeral for x.
According to Lemma 3 we have that
![]() $\bot $
,
$\bot $
,
![]() $\supset $
and
$\supset $
and
![]() $\rightarrow $
obey the classical introduction and elimination rules when the antecedent is a formula of
$\rightarrow $
obey the classical introduction and elimination rules when the antecedent is a formula of
![]() $\mathcal {L}^{\rightarrow }_{\mathbb {N}}$
. An important property of
$\mathcal {L}^{\rightarrow }_{\mathbb {N}}$
. An important property of
![]() ${\textbf {KFL}}$
is that it entails an object-linguistic version of the
${\textbf {KFL}}$
is that it entails an object-linguistic version of the
![]() $\texttt {Tr}$
-schema for sentences that do not contain the conditional
$\texttt {Tr}$
-schema for sentences that do not contain the conditional
![]() $\rightarrow $
. We will return to the philosophical implications of this property in Section 6.
$\rightarrow $
. We will return to the philosophical implications of this property in Section 6.
Lemma 8. The following are provable in
![]() ${\textbf {KFL}}$
:
${\textbf {KFL}}$
:
-
(i)

-
(ii) For
 $A\in \mathcal L_{\texttt {Tr}}$
,
$A\in \mathcal L_{\texttt {Tr}}$
,
 $\Rightarrow \texttt {Tr}\ulcorner A\urcorner \leftrightarrow A$
.
$\Rightarrow \texttt {Tr}\ulcorner A\urcorner \leftrightarrow A$
.
Proof. (i) is immediate by the axioms of
![]() ${\textbf {KFL}}$
, and (ii) is obtained by an external induction on the rank of A.□
${\textbf {KFL}}$
, and (ii) is obtained by an external induction on the rank of A.□
4.1 Semantics
The intended interpretation of our theory of truth is based on Kripke’s fixed point semantics [Reference Kripke18] and stems from the
![]() $\mathbf { HYPE}$
-models presented in Leitgeb [Reference Leitgeb19, sec. 7]. Our model will feature a state space, whose states are fixed-points of the usual monotone operator associated with the four-valued evaluation schema as stated in [Reference Visser29, Reference Woodruff30].
$\mathbf { HYPE}$
-models presented in Leitgeb [Reference Leitgeb19, sec. 7]. Our model will feature a state space, whose states are fixed-points of the usual monotone operator associated with the four-valued evaluation schema as stated in [Reference Visser29, Reference Woodruff30].
Let
![]() $\Phi \colon \mathcal {P}\omega \longrightarrow \mathcal {P}\omega $
be the monotone operator defined in [Reference Halbach14, lemma 15.6]: given some set X of codes of sentences of
$\Phi \colon \mathcal {P}\omega \longrightarrow \mathcal {P}\omega $
be the monotone operator defined in [Reference Halbach14, lemma 15.6]: given some set X of codes of sentences of
![]() $\mathcal L_{\texttt {Tr}}$
,
$\mathcal L_{\texttt {Tr}}$
,
![]() $\Phi (X)$
returns its closure under the
$\Phi (X)$
returns its closure under the
![]() $\mathbf {FDE}$
-evaluation. States will have the form
$\mathbf {FDE}$
-evaluation. States will have the form
![]() $(\mathbb {N}, S)$
, where S is a fixed point of
$(\mathbb {N}, S)$
, where S is a fixed point of
![]() $\Phi $
. Since we are interested in constant domains and in keeping the interpretation of the arithmetical vocabulary fixed, we omit reference to
$\Phi $
. Since we are interested in constant domains and in keeping the interpretation of the arithmetical vocabulary fixed, we omit reference to
![]() $\mathbb {N}$
and identify states with the fixed points themselves. Therefore, we let
$\mathbb {N}$
and identify states with the fixed points themselves. Therefore, we let
 $$ \begin{align*} & \mathbb{W}:=\{ X \subseteq \texttt{Sent}_{\mathcal L_{\texttt{Tr}}}\;|\; \Phi(X) = X \}, \tag{17} \\ & S \leq_{\mathbb{W}} S' :\Leftrightarrow S \subseteq S', \tag{18} \\ & S^* := \omega \setminus \overline{S}, \text{ with } \overline{X}=\{\neg \varphi\;|\; \varphi\in X\}, \tag{19} \\ & \text{the interpretation of } \texttt{Tr} \text{ is denoted with } \texttt{Tr}^S := S. \tag{20} \end{align*} $$
$$ \begin{align*} & \mathbb{W}:=\{ X \subseteq \texttt{Sent}_{\mathcal L_{\texttt{Tr}}}\;|\; \Phi(X) = X \}, \tag{17} \\ & S \leq_{\mathbb{W}} S' :\Leftrightarrow S \subseteq S', \tag{18} \\ & S^* := \omega \setminus \overline{S}, \text{ with } \overline{X}=\{\neg \varphi\;|\; \varphi\in X\}, \tag{19} \\ & \text{the interpretation of } \texttt{Tr} \text{ is denoted with } \texttt{Tr}^S := S. \tag{20} \end{align*} $$
The intended full model
![]() $\mathfrak {M}_{\Phi }$
is the
$\mathfrak {M}_{\Phi }$
is the
![]() $\mathbf {HYPE}$
model based on the frame
$\mathbf {HYPE}$
model based on the frame
![]() $( \mathbb {W},\leq _{\mathbb {W}}, * )$
with the constant domain
$( \mathbb {W},\leq _{\mathbb {W}}, * )$
with the constant domain
![]() $\omega $
. The intended minimal model
$\omega $
. The intended minimal model
![]() $\mathfrak {M}_{\Phi }^{\texttt {min}}$
is given by restricting the set of states to the minimal and maximal fixed points. By a straightforward induction on the height of the derivation in
$\mathfrak {M}_{\Phi }^{\texttt {min}}$
is given by restricting the set of states to the minimal and maximal fixed points. By a straightforward induction on the height of the derivation in
![]() ${\textbf {KFL}}$
, we obtain:
${\textbf {KFL}}$
, we obtain:
Lemma 9. If
![]() , then
, then
![]() .
.
4.2 Proof theory: lower bound
We show that
![]() ${\textbf {KFL}}$
can define (and therefore prove the well-foundedness of) Tarskian truth predicates for any
${\textbf {KFL}}$
can define (and therefore prove the well-foundedness of) Tarskian truth predicates for any
![]() $\alpha \prec \varepsilon _0$
. By the techniques employed in Feferman and Cantini’s analyses of the proof theory of
$\alpha \prec \varepsilon _0$
. By the techniques employed in Feferman and Cantini’s analyses of the proof theory of
![]() $\textbf {KF}$
[Reference Cantini1, Reference Feferman4], this entails that
$\textbf {KF}$
[Reference Cantini1, Reference Feferman4], this entails that
![]() ${\textbf {KFL}}$
can prove
${\textbf {KFL}}$
can prove
 $\texttt {TI}_{<\varphi _{\varepsilon _0}0}(\mathcal {L}_{\mathbb {N}})$
.
$\texttt {TI}_{<\varphi _{\varepsilon _0}0}(\mathcal {L}_{\mathbb {N}})$
.
We first define the Tarskian languages.
Definition 3. For
![]() $0\leq \alpha <\Gamma _0$
, we let
$0\leq \alpha <\Gamma _0$
, we let

We then write
 $$ \begin{align*} \texttt{Sent}_{\mathcal L_{\texttt{Tr}}}^{<\alpha}(x):\leftrightarrow\;& \exists \zeta \prec \alpha \,\texttt{Sent}_{\mathcal L_{\texttt{Tr}}}(\zeta,x), \\ \texttt{Tr}_{\alpha} (x) :\leftrightarrow \;& \texttt{Sent}^{< \alpha}_{\mathcal L_{\texttt{Tr}}} (x) \wedge \texttt{Tr} (x). \end{align*} $$
$$ \begin{align*} \texttt{Sent}_{\mathcal L_{\texttt{Tr}}}^{<\alpha}(x):\leftrightarrow\;& \exists \zeta \prec \alpha \,\texttt{Sent}_{\mathcal L_{\texttt{Tr}}}(\zeta,x), \\ \texttt{Tr}_{\alpha} (x) :\leftrightarrow \;& \texttt{Sent}^{< \alpha}_{\mathcal L_{\texttt{Tr}}} (x) \wedge \texttt{Tr} (x). \end{align*} $$
As we mentioned in Section 3, the arithmetical vocabulary behaves classically in
![]() ${\textbf {KFL}}$
.
${\textbf {KFL}}$
.
Lemma 10.
![]() .
.
Proof. By formal induction on the complexity of the ‘sentence’
![]() $x\in \mathcal {L}_{\mathbb {N}}$
.□
$x\in \mathcal {L}_{\mathbb {N}}$
.□
The next two claims establish that the previous fact can be extended to all Tarskian languages whose indices can be proved to be well-founded. First, one shows that the claim ‘sentences in
 $\texttt {Sent}_{\mathcal L_{\texttt {Tr}}}^{<\eta }$
are either determinately true or determinately false’ is progressive.
$\texttt {Sent}_{\mathcal L_{\texttt {Tr}}}^{<\eta }$
are either determinately true or determinately false’ is progressive.
Lemma 11.
![]() ${\textbf {KFL}}$
proves:
${\textbf {KFL}}$
proves:
Proof. By the definition of
![]() $\texttt {OT}$
,
$\texttt {OT}$
,
![]() ${\textbf {KFL}}$
proves that
${\textbf {KFL}}$
proves that
![]() $\eta \in \texttt {OT}$
is either
$\eta \in \texttt {OT}$
is either
![]() $0$
, or a successor ordinal, or a limit. By arguing informally in
$0$
, or a successor ordinal, or a limit. By arguing informally in
![]() ${\textbf {KFL}}$
, we show that the statement of the lemma holds, thereby establishing the claim.
${\textbf {KFL}}$
, we show that the statement of the lemma holds, thereby establishing the claim.
Lemma 10 gives us the base case. The limit case follows immediately by the definition of
![]() $\texttt {Sent}_{\mathcal L_{\texttt {Tr}}}(\lambda ,x)$
. For the successor step, one needs to establish (cf.[Reference Nicolai22, lemma 7]):
$\texttt {Sent}_{\mathcal L_{\texttt {Tr}}}(\lambda ,x)$
. For the successor step, one needs to establish (cf.[Reference Nicolai22, lemma 7]):
Claim (21) is obtained by a formal induction on the complexity of y. Crucially, the proof rests on the following
![]() ${\textbf {KFL}}$
-derivable claims, which provide the cases required by the induction:
${\textbf {KFL}}$
-derivable claims, which provide the cases required by the induction:

□
By Theorem 1, we obtain:
Corollary 3. For any
![]() $\alpha < \varepsilon _0$
,
$\alpha < \varepsilon _0$
,
![]() .
.
Since, by Theorem 1,
![]() ${\textbf {KFL}}$
proves transfinite induction up to ordinals smaller than
${\textbf {KFL}}$
proves transfinite induction up to ordinals smaller than
![]() $\varepsilon _0$
, it follows that we are able to establish the fundamental properties of Tarskian truth predicates up to any ordinal smaller than
$\varepsilon _0$
, it follows that we are able to establish the fundamental properties of Tarskian truth predicates up to any ordinal smaller than
![]() $\varepsilon _0$
. For
$\varepsilon _0$
. For
![]() $\alpha <\Gamma _0$
,
$\alpha <\Gamma _0$
,
![]() $\mathbf { RT}_{<\alpha }$
refers to the theory of ramified truth predicates up to
$\mathbf { RT}_{<\alpha }$
refers to the theory of ramified truth predicates up to
![]() $\alpha $
, as defined in [Reference Halbach14, sec. 9.1].
$\alpha $
, as defined in [Reference Halbach14, sec. 9.1].
Corollary 4.
![]() ${\textbf {KFL}}$
defines the truth predicates of
${\textbf {KFL}}$
defines the truth predicates of
![]() $\mathbf {RT}_{<\alpha }$
, for
$\mathbf {RT}_{<\alpha }$
, for
![]() $\alpha \prec \varepsilon _0$
.
$\alpha \prec \varepsilon _0$
.
By the proof-theoretic equivalence of systems of ramified truth and ramified analysis established by Feferman [Reference Feferman2, Reference Feferman4], we obtain:
Corollary 5.
![]() ${\textbf {KFL}}$
proves
${\textbf {KFL}}$
proves
 $\texttt {TI}_{<\varphi _{\varepsilon _0}0}(\mathcal {L}_{\mathbb {N}})$
.
$\texttt {TI}_{<\varphi _{\varepsilon _0}0}(\mathcal {L}_{\mathbb {N}})$
.
Feferman and Cantini established that
![]() $\textbf {KF}$
is proof-theoretically equivalent to
$\textbf {KF}$
is proof-theoretically equivalent to
![]() $\mathbf {RT}_{<\varepsilon _0}$
. Our results so far then establish that
$\mathbf {RT}_{<\varepsilon _0}$
. Our results so far then establish that
![]() ${\textbf {KFL}}$
is proof-theoretically at least as strong as
${\textbf {KFL}}$
is proof-theoretically at least as strong as
![]() $\textbf {KF}$
. In subsection 4.3, we will show that
$\textbf {KF}$
. In subsection 4.3, we will show that
![]() ${\textbf {KFL}}$
and
${\textbf {KFL}}$
and
![]() $\textbf {KF}$
are in fact proof-theoretically equivalent.
$\textbf {KF}$
are in fact proof-theoretically equivalent.
4.3 Proof theory: upper bound
We interpret
![]() ${\textbf {KFL}}$
in the Kripke–Feferman system
${\textbf {KFL}}$
in the Kripke–Feferman system
![]() $\textbf {KF}$
. For definiteness, we consider the version of
$\textbf {KF}$
. For definiteness, we consider the version of
![]() $\textbf {KF}$
formulated in a language
$\textbf {KF}$
formulated in a language
![]() $\mathcal {L}_{{\mathbb {T,F}}}$
featuring truth (
$\mathcal {L}_{{\mathbb {T,F}}}$
featuring truth (
![]() $\mathbb {T}$
) and falsity (
$\mathbb {T}$
) and falsity (
![]() $\mathbb {F}$
) predicates. Such a version of
$\mathbb {F}$
) predicates. Such a version of
![]() $\textbf {KF}$
is basically the one presented in [Reference Cantini1, sec. 2], but without the consistency axiom that rules out truth-value gluts.
$\textbf {KF}$
is basically the one presented in [Reference Cantini1, sec. 2], but without the consistency axiom that rules out truth-value gluts.
In order to interpret
![]() ${\textbf {KFL}}$
into
${\textbf {KFL}}$
into
![]() $\textbf {KF}$
, we consider a two-layered translation that differentiates between the external and internal structures of
$\textbf {KF}$
, we consider a two-layered translation that differentiates between the external and internal structures of
![]() $\mathcal L_{\texttt {Tr}}^{\rightarrow }$
-formulas. Essentially, the external translation fully commutes with negation, and translates the
$\mathcal L_{\texttt {Tr}}^{\rightarrow }$
-formulas. Essentially, the external translation fully commutes with negation, and translates the
![]() $\mathbf { HYPE}$
conditional as classical material implication. The internal translation treats negated truth ascriptions as falsity ascriptions, and is defined by an induction on the positive complexity of formulas that adheres to the semantic clauses of
$\mathbf { HYPE}$
conditional as classical material implication. The internal translation treats negated truth ascriptions as falsity ascriptions, and is defined by an induction on the positive complexity of formulas that adheres to the semantic clauses of
![]() $\mathbf {FDE}$
-style fixed-point models. The internal translation therefore translates truth and non-truth of
$\mathbf {FDE}$
-style fixed-point models. The internal translation therefore translates truth and non-truth of
![]() ${\textbf {KFL}}$
as truth and falsity of
${\textbf {KFL}}$
as truth and falsity of
![]() $\textbf {KF}$
, respectively. Since we want to uniformly translate formulas and their codes inside the truth predicate, we essentially employ the recursion theorem, as described for instance by [Reference Halbach14, sec. 5.3].
$\textbf {KF}$
, respectively. Since we want to uniformly translate formulas and their codes inside the truth predicate, we essentially employ the recursion theorem, as described for instance by [Reference Halbach14, sec. 5.3].
Definition 4. We define the translations
![]() $\tau \colon \mathcal L_{\texttt {Tr}} \longrightarrow \mathcal {L}_{{\mathbb {T,F}}}$
, and
$\tau \colon \mathcal L_{\texttt {Tr}} \longrightarrow \mathcal {L}_{{\mathbb {T,F}}}$
, and
![]() $\sigma \colon \mathcal L_{\texttt {Tr}}^{\rightarrow }\longrightarrow \mathcal {L}_{{\mathbb {T,F}}}$
as follows:
$\sigma \colon \mathcal L_{\texttt {Tr}}^{\rightarrow }\longrightarrow \mathcal {L}_{{\mathbb {T,F}}}$
as follows:
-
(i)
 $$ \begin{align*} &( s = t)^{\tau}= s = t & & ( s \neq t)^{\tau}= s \neq t \\ &(\texttt{Tr} \,t)^{\tau}={\mathbb T}\tau(t) &&(\neg \texttt{Tr}\, t)^{\tau}= {\mathbb F}\tau(t)\\ &(\neg\neg \varphi)^{\tau}=(\varphi)^{\tau}\\ &(\varphi\vee \psi)^{\tau}=(\varphi)^{\tau}\vee (\psi)^{\tau}&&(\neg(\varphi\vee\psi))^{\tau}=(\neg \varphi)^{\tau}\land (\neg \psi)^{\tau}\\ &(\forall x\varphi)^{\tau}=\forall x \varphi^{\tau}&&(\neg\forall x\varphi)^{\tau}=\exists x (\neg \varphi)^{\tau}. \end{align*} $$
$$ \begin{align*} &( s = t)^{\tau}= s = t & & ( s \neq t)^{\tau}= s \neq t \\ &(\texttt{Tr} \,t)^{\tau}={\mathbb T}\tau(t) &&(\neg \texttt{Tr}\, t)^{\tau}= {\mathbb F}\tau(t)\\ &(\neg\neg \varphi)^{\tau}=(\varphi)^{\tau}\\ &(\varphi\vee \psi)^{\tau}=(\varphi)^{\tau}\vee (\psi)^{\tau}&&(\neg(\varphi\vee\psi))^{\tau}=(\neg \varphi)^{\tau}\land (\neg \psi)^{\tau}\\ &(\forall x\varphi)^{\tau}=\forall x \varphi^{\tau}&&(\neg\forall x\varphi)^{\tau}=\exists x (\neg \varphi)^{\tau}. \end{align*} $$
-
(ii)
 $$ \begin{align*} &(s = t)^{\sigma} = s = t \\ &(\texttt{Tr} \,t)^{\sigma}={\mathbb T}\tau(t) && \\ &(\neg\varphi)^{\sigma}=\begin{cases} {\mathbb F}\tau(t), \text{if } \varphi \text{ is } \texttt{Tr} \,t,\\ s\neq t, \text{if } \varphi \text{ is } s=t,\\ \neg\varphi^{\sigma}, \text{else.} \end{cases}&& \\ &(\varphi \vee \psi)^{\sigma}=(\varphi)^{\sigma} \vee (\psi)^{\sigma}\\ &(\forall x \varphi)^{\sigma} = \forall x \varphi^{\sigma}\\ &(\varphi\rightarrow \psi)^{\sigma}= \neg (\varphi)^{\sigma} \vee (\psi)^{\sigma}. \end{align*} $$
$$ \begin{align*} &(s = t)^{\sigma} = s = t \\ &(\texttt{Tr} \,t)^{\sigma}={\mathbb T}\tau(t) && \\ &(\neg\varphi)^{\sigma}=\begin{cases} {\mathbb F}\tau(t), \text{if } \varphi \text{ is } \texttt{Tr} \,t,\\ s\neq t, \text{if } \varphi \text{ is } s=t,\\ \neg\varphi^{\sigma}, \text{else.} \end{cases}&& \\ &(\varphi \vee \psi)^{\sigma}=(\varphi)^{\sigma} \vee (\psi)^{\sigma}\\ &(\forall x \varphi)^{\sigma} = \forall x \varphi^{\sigma}\\ &(\varphi\rightarrow \psi)^{\sigma}= \neg (\varphi)^{\sigma} \vee (\psi)^{\sigma}. \end{align*} $$
![]() ${\textbf {KFL}}$
-proofs can then be turned, by the translation
${\textbf {KFL}}$
-proofs can then be turned, by the translation
![]() $\sigma $
, into
$\sigma $
, into
![]() $\textbf {KF}$
-proofs, as the next proposition shows.
$\textbf {KF}$
-proofs, as the next proposition shows.
Proposition 2. If
![]() , then
, then
![]() .
.
Proof. The proof is by induction on the height of the derivation in
![]() ${\textbf {KFL}}$
and follows almost directly from the definition of the translation
${\textbf {KFL}}$
and follows almost directly from the definition of the translation
![]() $\sigma $
. Only the case of (KFL3) is slightly more involved: we require that (with
$\sigma $
. Only the case of (KFL3) is slightly more involved: we require that (with
![]() $\equiv $
expressing material equivalence)
$\equiv $
expressing material equivalence)
However, this can be proved by formal induction on the complexity of x.□
The combination of Proposition 2 and Corollary 4 yields that
![]() $\textbf {KF}$
and
$\textbf {KF}$
and
![]() ${\textbf {KFL}}$
have the same arithmetical theorems, and in particular they have the same proof-theoretic ordinal—cf. [Reference Pohlers23, sec. 6.7].
${\textbf {KFL}}$
have the same arithmetical theorems, and in particular they have the same proof-theoretic ordinal—cf. [Reference Pohlers23, sec. 6.7].
Corollary 6.
![]() $|{\textbf {KFL}}|=|\textbf {KF}|=\varphi _{\varepsilon _0}0$
.
$|{\textbf {KFL}}|=|\textbf {KF}|=\varphi _{\varepsilon _0}0$
.
In Section 5, we extend our results to schematic extensions of
![]() ${\textbf {KFL}}$
and
${\textbf {KFL}}$
and
![]() $\textbf {KF}$
.
$\textbf {KF}$
.
5 Schematic extension
5.1
 $\textbf {KFL}^{*}$
: rules and semantics
$\textbf {KFL}^{*}$
: rules and semantics
In this section we study the schematic extension of
![]() ${\textbf {KFL}}$
in the sense of [Reference Feferman4]. This is obtained by extending
${\textbf {KFL}}$
in the sense of [Reference Feferman4]. This is obtained by extending
![]() ${\textbf {KFL}}$
with a special substitution rule that enables us to uniformly replace the distinguished predicate P in arithmetical theorems
${\textbf {KFL}}$
with a special substitution rule that enables us to uniformly replace the distinguished predicate P in arithmetical theorems
![]() $A(P)$
of our extended theory for arbitrary formulas of
$A(P)$
of our extended theory for arbitrary formulas of
![]() $\mathcal L_{\texttt {Tr}}^{\rightarrow }$
. More precisely, following Feferman, we will employ a schematic language
$\mathcal L_{\texttt {Tr}}^{\rightarrow }$
. More precisely, following Feferman, we will employ a schematic language
![]() $\mathcal L_{\texttt {Tr}}^{\rightarrow } (P)$
(and sub-languages thereof) featuring a fresh schematic predicate symbol P, which is assumed to behave classically.
$\mathcal L_{\texttt {Tr}}^{\rightarrow } (P)$
(and sub-languages thereof) featuring a fresh schematic predicate symbol P, which is assumed to behave classically.
Definition 5. The system
![]() $\textbf {KFL}^{*}$
in
$\textbf {KFL}^{*}$
in
![]() $\mathcal L_{\texttt {Tr}}^{\rightarrow } (P)$
extends
$\mathcal L_{\texttt {Tr}}^{\rightarrow } (P)$
extends
![]() ${\textbf {KFL}}$
with:
${\textbf {KFL}}$
with:
-
(i) The induction schema
 $\texttt {IND}^{\rightarrow }(\mathcal L_{\texttt {Tr}}^{\rightarrow } (P));$
$\texttt {IND}^{\rightarrow }(\mathcal L_{\texttt {Tr}}^{\rightarrow } (P));$
-
(ii)
 $\forall x (P (x) \vee \neg P(x));$
$\forall x (P (x) \vee \neg P(x));$
-
(iii) Disquotational axiom for
 $P$
: (KFLP)
$P$
: (KFLP)
-
(iv) The substitution rule:

The properties of
![]() ${\textbf {KFL}}$
expressed by Lemma 8 transfer directly to
${\textbf {KFL}}$
expressed by Lemma 8 transfer directly to
![]() $\textbf {KFL}^{*}$
, and are proved in an analogous fashion.
$\textbf {KFL}^{*}$
, and are proved in an analogous fashion.
The semantics given in Section 4.1 can be modified to provide a class of fixed-point models for
![]() $\textbf {KFL}^{*}$
. We call
$\textbf {KFL}^{*}$
. We call
![]() $\Phi _X$
the result of relativizing the operator from Section 4.1 to an arbitrary
$\Phi _X$
the result of relativizing the operator from Section 4.1 to an arbitrary
![]() $X\subseteq \omega $
.Footnote
8
In particular, this means supplementing the positive inductive definition associated with
$X\subseteq \omega $
.Footnote
8
In particular, this means supplementing the positive inductive definition associated with
![]() $\Phi $
with the clause:
$\Phi $
with the clause:
a sentence
![]() $P z$
, with z a closed term of
$P z$
, with z a closed term of
![]() $\mathcal L_{\texttt {Tr}}$
, is in the extension of the truth predicate (relativized to X) iff
$\mathcal L_{\texttt {Tr}}$
, is in the extension of the truth predicate (relativized to X) iff
![]() $\texttt {val}(z)\in X$
.
$\texttt {val}(z)\in X$
.
This modification clearly does not compromise the monotonicity of the operator. Therefore, let
![]() $\texttt {MIN}_{\Phi _X}$
be the minimal fixed point of
$\texttt {MIN}_{\Phi _X}$
be the minimal fixed point of
![]() $\Phi _X$
, and
$\Phi _X$
, and
![]() $\texttt {MAX}_{\Phi _X}$
its maximal one. For any X, we then obtain the minimal
$\texttt {MAX}_{\Phi _X}$
its maximal one. For any X, we then obtain the minimal
![]() $\mathbf {HYPE}$
model
$\mathbf {HYPE}$
model
 $$ \begin{align*} \mathfrak{M}^{\texttt{min}}_{\Phi_X}:=(\{\texttt{MIN}_{\Phi_X},\texttt{MAX}_{\Phi_X}\},\subseteq, *). \end{align*} $$
$$ \begin{align*} \mathfrak{M}^{\texttt{min}}_{\Phi_X}:=(\{\texttt{MIN}_{\Phi_X},\texttt{MAX}_{\Phi_X}\},\subseteq, *). \end{align*} $$
Again in
 $\mathfrak {M}^{\texttt {min}}_{\Phi _X}$
all arithmetical vocabulary is interpreted standardly at its two states (fixed-points). Only the interpretation of the truth predicate varies. Our notation reflects this.
$\mathfrak {M}^{\texttt {min}}_{\Phi _X}$
all arithmetical vocabulary is interpreted standardly at its two states (fixed-points). Only the interpretation of the truth predicate varies. Our notation reflects this.
Proposition 3. If
![]() , then for all X,
, then for all X,
 .
.
Proof. By induction on the length of the derivation in
![]() $\textbf {KFL}^{*}$
.
$\textbf {KFL}^{*}$
.
We consider the case of the substitution rule applied to an arithmetical sequent
. That is, our proof ends with

with
![]() $B(x)$
an arbitrary formula of
$B(x)$
an arbitrary formula of
![]() $\mathcal L_{\texttt {Tr}}^{\rightarrow }$
.
$\mathcal L_{\texttt {Tr}}^{\rightarrow }$
.
By induction hypothesis, for all X,
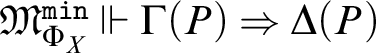
. Since
is arithmetical, for all interpretations Y of P,
. Then, following [Reference Feferman4], we can let Y be

to obtain that

□
5.2 Proof-theoretic analysis
We first consider the proof-theoretic lower-bound for
![]() $\textbf {KFL}^{*}$
. We adapt to the present setting the strategy outlined in [Reference Feferman and Strahm6, p. 84]. In particular, Feferman and Strahm formalize the notion of A-jump hierarchy, which is a hierarchy of sets of natural numbers obtained by iterating an arithmetical operator expressed by an arithmetical formula
$\textbf {KFL}^{*}$
. We adapt to the present setting the strategy outlined in [Reference Feferman and Strahm6, p. 84]. In particular, Feferman and Strahm formalize the notion of A-jump hierarchy, which is a hierarchy of sets of natural numbers obtained by iterating an arithmetical operator expressed by an arithmetical formula
![]() $A(X,\theta ,y)$
. An A-jump hierarchy is relativized when the starting point is a specific set of natural numbers expressed by some predicate P. The notion of A-jump hierarchy is quite general, and has as special cases familiar hierarchies such as the Turing-jump hierarchy.
$A(X,\theta ,y)$
. An A-jump hierarchy is relativized when the starting point is a specific set of natural numbers expressed by some predicate P. The notion of A-jump hierarchy is quite general, and has as special cases familiar hierarchies such as the Turing-jump hierarchy.
For our purposes, it’s useful to consider A-jump hierarchies in which membership in second-order parameters is replaced by the notion of satisfaction. In order to achieve this, we employ Feferman’s strategy in [Reference Feferman4] in which the stages of the Turing jump-hierarchy are represented by means of suitable primitive recursive functions on codes of
![]() $\mathcal L_{\texttt {Tr}}$
-formulas. Specifically, we encode in suitable primitive recursive functions the stages of a hierarchy in which the formula A is the Veblen-jump formula that will be introduced shortly.
$\mathcal L_{\texttt {Tr}}$
-formulas. Specifically, we encode in suitable primitive recursive functions the stages of a hierarchy in which the formula A is the Veblen-jump formula that will be introduced shortly.
We denote with
![]() ${A}(\texttt {Tr} f^A,\eta ,y)$
the result of replacing every occurrence of
${A}(\texttt {Tr} f^A,\eta ,y)$
the result of replacing every occurrence of
![]() $(u, v) \in X$
in
$(u, v) \in X$
in
![]() $A(X,\eta ,y)$
with
$A(X,\eta ,y)$
with
where the functions
![]() $f^A_x(y)$
are recursively defined as follows:
$f^A_x(y)$
are recursively defined as follows:

In the clause for
![]() $f^{A,\zeta }$
, the input x is intended to be an ordered pair
$f^{A,\zeta }$
, the input x is intended to be an ordered pair
![]() $(x_0,x_1)$
. As in the definitions of translations
$(x_0,x_1)$
. As in the definitions of translations
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
above, the existence of the function
$\tau $
above, the existence of the function
![]() $f^A$
can be obtained by employing the recursion theorem, as it needs to apply to its arithmetical code.
$f^A$
can be obtained by employing the recursion theorem, as it needs to apply to its arithmetical code.
Recall the general pattern of the Gentzen jump formula—with
![]() $\rightarrow $
the
$\rightarrow $
the
![]() $\mathbf {HYPE}$
conditional:
$\mathbf {HYPE}$
conditional:
We build our
![]() $\mathcal {A}$
-hierarchy on the more complex Veblen-jump formula
$\mathcal {A}$
-hierarchy on the more complex Veblen-jump formula
![]() $\mathcal {A}$
, as stated by Schütte in [Reference Schütte24, p. 185], which is crucial for the proof-theoretic analysis of predicative systems.
$\mathcal {A}$
, as stated by Schütte in [Reference Schütte24, p. 185], which is crucial for the proof-theoretic analysis of predicative systems.
One first defines the functions:
 $$ \begin{align*} \begin{array}{ll} \texttt{e}(0)=0 & \texttt{h}(0)=0\\ \texttt{e}(\omega^{\eta})=\eta & \texttt{h}(\omega^{\eta})=0\\ \texttt{e}(\omega^{\eta_1}+\cdots +\omega^{\eta_n})=\eta_n &\texttt{h}(\omega^{\eta_1}+\cdots +\omega^{\eta_n})=\omega^{\eta_1}+\cdots +\omega^{\eta_{n-1}} \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \texttt{e}(0)=0 & \texttt{h}(0)=0\\ \texttt{e}(\omega^{\eta})=\eta & \texttt{h}(\omega^{\eta})=0\\ \texttt{e}(\omega^{\eta_1}+\cdots +\omega^{\eta_n})=\eta_n &\texttt{h}(\omega^{\eta_1}+\cdots +\omega^{\eta_n})=\omega^{\eta_1}+\cdots +\omega^{\eta_{n-1}} \end{array} \end{align*} $$
with
![]() $\eta _n\preceq \cdots \preceq \eta _1$
.
$\eta _n\preceq \cdots \preceq \eta _1$
.
The Veblen-jump formula
![]() $\mathcal {A}$
is then the following:
$\mathcal {A}$
is then the following:
 $$ \begin{align*} \mathcal{A} (\texttt{Tr} f^{\mathcal{A}} ,\xi, y) := \forall \zeta (\texttt{h}(\xi) \preccurlyeq \zeta \prec \xi \, \mathcal{J} ( \texttt{Tr} f^{\mathcal{A}}_{\zeta} , \varphi_{\texttt{e}(\xi)}y)). \end{align*} $$
$$ \begin{align*} \mathcal{A} (\texttt{Tr} f^{\mathcal{A}} ,\xi, y) := \forall \zeta (\texttt{h}(\xi) \preccurlyeq \zeta \prec \xi \, \mathcal{J} ( \texttt{Tr} f^{\mathcal{A}}_{\zeta} , \varphi_{\texttt{e}(\xi)}y)). \end{align*} $$
It expresses that, given some ordinal
![]() $\xi $
, the
$\xi $
, the
![]() $\mathcal {A}$
-jump hierarchy in the interval between the ordinal
$\mathcal {A}$
-jump hierarchy in the interval between the ordinal
![]() $\texttt {h}(\xi )$
and
$\texttt {h}(\xi )$
and
![]() $\xi $
itself is closed under the Gentzen jump relative to
$\xi $
itself is closed under the Gentzen jump relative to
![]() $\varphi _{\texttt {e}(\xi )}y$
(with y a parameter). In the following we will omit the superscripts specifying the formula, since we will keep
$\varphi _{\texttt {e}(\xi )}y$
(with y a parameter). In the following we will omit the superscripts specifying the formula, since we will keep
![]() $\mathcal A$
fixed.
$\mathcal A$
fixed.
An essential ingredient of the lower-bound proof for
![]() $\textbf {KFL}^{*}$
is the ‘disquotational’ behavior of our truth predicate for stages in the hierarchy that are provably well-founded.
$\textbf {KFL}^{*}$
is the ‘disquotational’ behavior of our truth predicate for stages in the hierarchy that are provably well-founded.
Lemma 12. If we have
![]() $\texttt {TI}_{\alpha }(\mathcal L_{\texttt {Tr}}^{\rightarrow })$
, then for all
$\texttt {TI}_{\alpha }(\mathcal L_{\texttt {Tr}}^{\rightarrow })$
, then for all
![]() $\eta $
, with
$\eta $
, with
![]() $0 \prec \eta \prec \alpha $
$0 \prec \eta \prec \alpha $

Proof. For all
![]() $\eta $
and all n, we can show that
$\eta $
and all n, we can show that
![]() $\texttt {Sent}_{\eta } (f^{\eta }((n_0,n_1)))$
and
$\texttt {Sent}_{\eta } (f^{\eta }((n_0,n_1)))$
and
![]() $\texttt {Sent}_{\eta } (f_{\eta } (n))$
by transfinite induction on
$\texttt {Sent}_{\eta } (f_{\eta } (n))$
by transfinite induction on
![]() $\eta $
making use of the properties of the ramified truth predicates such as, for
$\eta $
making use of the properties of the ramified truth predicates such as, for
![]() $\lambda \prec \alpha $
limit:
$\lambda \prec \alpha $
limit:
 $$ \begin{align*} \forall \zeta \prec \lambda \big( \texttt{Tr}_{\lambda} (\texttt{Tr}_{\zeta} t)\leftrightarrow \texttt{Tr}_{\zeta}\texttt{val}(t)\big). \end{align*} $$
$$ \begin{align*} \forall \zeta \prec \lambda \big( \texttt{Tr}_{\lambda} (\texttt{Tr}_{\zeta} t)\leftrightarrow \texttt{Tr}_{\zeta}\texttt{val}(t)\big). \end{align*} $$
Such properties just state that Tarskian truth predicates are fully compositional for ordinals for which we have transfinite induction ([Reference Feferman4], [Reference Halbach14, sec. 9.1]).
Since all truth predicates in
 are provably compositional by
are provably compositional by
![]() $\texttt {TI}_{\alpha }(\mathcal L_{\texttt {Tr}}^{\rightarrow })$
, the claim is obtained by the fact that full compositionality entails disquotation as shown by [Reference Tarski, Berka and Kreiser27].□
$\texttt {TI}_{\alpha }(\mathcal L_{\texttt {Tr}}^{\rightarrow })$
, the claim is obtained by the fact that full compositionality entails disquotation as shown by [Reference Tarski, Berka and Kreiser27].□
The disquotational properties allow us to establish some fundamental properties of the
![]() $\mathcal {A}$
-jump hierarchy. In particular, we show that the
$\mathcal {A}$
-jump hierarchy. In particular, we show that the
![]() $\mathcal {A}$
-jump hierarchy can be elegantly expressed by truth ascriptions on the functions
$\mathcal {A}$
-jump hierarchy can be elegantly expressed by truth ascriptions on the functions
![]() $f_{\alpha }$
. This is because the truth predicate enables us to quantify over the stages of the construction of the
$f_{\alpha }$
. This is because the truth predicate enables us to quantify over the stages of the construction of the
![]() $\mathcal {A}$
-jump hierarchy, and also to retrieve specific information about all the previous stages of the hierarchy, thanks to the disquotational property.
$\mathcal {A}$
-jump hierarchy, and also to retrieve specific information about all the previous stages of the hierarchy, thanks to the disquotational property.
Lemma 13. If
![]() $\texttt {TI}_{\alpha }(\mathcal L_{\texttt {Tr}}^{\rightarrow })$
is derivable in
$\texttt {TI}_{\alpha }(\mathcal L_{\texttt {Tr}}^{\rightarrow })$
is derivable in
![]() $\textbf {KFL}^{*}$
for some
$\textbf {KFL}^{*}$
for some
![]() $\alpha> 0$
, then we can derive in
$\alpha> 0$
, then we can derive in
![]() $\textbf {KFL}^{*}$
:
$\textbf {KFL}^{*}$
:
 $$ \begin{align*} \forall y ( P (y) \!\!\leftrightarrow\!\! \texttt{Tr} f_0 (y)) \wedge \forall\! \zeta [& 0 \prec \zeta \prec \alpha\!\!\rightarrow\!\! \forall\! y [ \texttt{Tr} f_{\zeta} (y) \!\!\leftrightarrow\!\! \forall z ( \texttt{h} (\zeta) \preccurlyeq z \prec \zeta \\&\quad\rightarrow\! \mathcal{J}(\texttt{Tr} f_z,\varphi_{\texttt{e}(\zeta)}y)) ]]. \end{align*} $$
$$ \begin{align*} \forall y ( P (y) \!\!\leftrightarrow\!\! \texttt{Tr} f_0 (y)) \wedge \forall\! \zeta [& 0 \prec \zeta \prec \alpha\!\!\rightarrow\!\! \forall\! y [ \texttt{Tr} f_{\zeta} (y) \!\!\leftrightarrow\!\! \forall z ( \texttt{h} (\zeta) \preccurlyeq z \prec \zeta \\&\quad\rightarrow\! \mathcal{J}(\texttt{Tr} f_z,\varphi_{\texttt{e}(\zeta)}y)) ]]. \end{align*} $$
Proof. By our disquotational axioms for P, it immediately follows that
![]() $\forall y ( P(y) \leftrightarrow \texttt {Tr} f_0 (y) )$
.
$\forall y ( P(y) \leftrightarrow \texttt {Tr} f_0 (y) )$
.
Let’s assume now that
![]() $0 \prec \zeta \prec \alpha $
. We have
$0 \prec \zeta \prec \alpha $
. We have

the right hand side is equivalent by the disquotational property to
By the definition of
![]() $f^{\zeta }$
, the latter formula is in turn equivalent to
$f^{\zeta }$
, the latter formula is in turn equivalent to
which is again equivalent to

By applying the disquotational property to (27), we obtain
□
Just like the Gentzen jump enabled us to establish the preservation of properties via ‘steps’ determined by fundamental sequence of ordinals
![]() $\omega _n$
up to
$\omega _n$
up to
![]() $\varepsilon _0$
, the Veblen jump allows us to establish the preservation of properties along the ‘steps’ governed by a fundamental sequence of ordinals up to
$\varepsilon _0$
, the Veblen jump allows us to establish the preservation of properties along the ‘steps’ governed by a fundamental sequence of ordinals up to
![]() $\Gamma _0$
. The progressiveness of the Veblen jump is the main engine that enables us to climb the
$\Gamma _0$
. The progressiveness of the Veblen jump is the main engine that enables us to climb the
![]() $\mathcal {A}$
-hierarchy: this is what the next lemma establishes, which is analogous to Schütte’s Lemma 9 in [Reference Schütte24, p. 186], a lemma that has become a standard tool in predicative proof-theory.
$\mathcal {A}$
-hierarchy: this is what the next lemma establishes, which is analogous to Schütte’s Lemma 9 in [Reference Schütte24, p. 186], a lemma that has become a standard tool in predicative proof-theory.
Lemma 14. If
![]() $\texttt {TI}_{\alpha }(\mathcal L_{\texttt {Tr}}^{\rightarrow })$
is provable in
$\texttt {TI}_{\alpha }(\mathcal L_{\texttt {Tr}}^{\rightarrow })$
is provable in
![]() $\textbf {KFL}^{*}$
for
$\textbf {KFL}^{*}$
for
![]() $\alpha <\Gamma _0$
, then
$\alpha <\Gamma _0$
, then
![]() $\textbf {KFL}^{*}$
proves
$\textbf {KFL}^{*}$
proves
Proof. Let
![]() $\texttt {l}(\cdot )$
be the function that keeps track of the syntactic complexity of an ordinal code. One first shows that the following claims
$\texttt {l}(\cdot )$
be the function that keeps track of the syntactic complexity of an ordinal code. One first shows that the following claims
 $$ \begin{align*} & \zeta\prec \alpha \tag{28} \\ & \forall x \prec \zeta \,\texttt{Prog} (\texttt{Tr} f_x) \tag{29} \\ & \forall y\prec \eta \,\texttt{Tr} f_{\zeta} (y) \tag{30} \\ & \forall y(\texttt{l}(y)<\texttt{l}(\theta)\rightarrow (y \prec \varphi_{\texttt{e}(\zeta)} \eta \rightarrow ( \forall z ( \texttt{h} (\zeta ) \preccurlyeq z \prec \zeta \rightarrow \mathcal{J} ( \texttt{Tr} f_z, y)))) \tag{31} \\ & \theta \prec \varphi_{\texttt{e} (\zeta)}\eta \tag{32} \\ & \texttt{h}(\zeta)\preceq \xi\prec \zeta \tag{33} \end{align*} $$
$$ \begin{align*} & \zeta\prec \alpha \tag{28} \\ & \forall x \prec \zeta \,\texttt{Prog} (\texttt{Tr} f_x) \tag{29} \\ & \forall y\prec \eta \,\texttt{Tr} f_{\zeta} (y) \tag{30} \\ & \forall y(\texttt{l}(y)<\texttt{l}(\theta)\rightarrow (y \prec \varphi_{\texttt{e}(\zeta)} \eta \rightarrow ( \forall z ( \texttt{h} (\zeta ) \preccurlyeq z \prec \zeta \rightarrow \mathcal{J} ( \texttt{Tr} f_z, y)))) \tag{31} \\ & \theta \prec \varphi_{\texttt{e} (\zeta)}\eta \tag{32} \\ & \texttt{h}(\zeta)\preceq \xi\prec \zeta \tag{33} \end{align*} $$
entail
![]() $\mathcal {J}(\texttt {Tr} f_{\xi },\theta )$
.
$\mathcal {J}(\texttt {Tr} f_{\xi },\theta )$
.
First we apply the principle of induction on the syntactic composition of ordinal codes [Reference Schütte24, theorem 20.10, p. 173] (provable in
![]() $\textbf {KFL}^{*}$
):
$\textbf {KFL}^{*}$
):
to the formula
Since we can prove that
 $$ \begin{align*} \forall x & \prec \zeta \,\texttt{Prog}(\texttt{Tr} f_x)\rightarrow \big( \forall y\prec \theta \, (\texttt{l}(y)<\texttt{l}(\theta) \rightarrow (y\prec \varphi_{\texttt{e}(\zeta)}\theta \rightarrow \forall z(\texttt{h}(\zeta)\preccurlyeq z \\ &\prec \zeta \;\mathcal{J}(\texttt{Tr} f_z,y))))\big), \end{align*} $$
$$ \begin{align*} \forall x & \prec \zeta \,\texttt{Prog}(\texttt{Tr} f_x)\rightarrow \big( \forall y\prec \theta \, (\texttt{l}(y)<\texttt{l}(\theta) \rightarrow (y\prec \varphi_{\texttt{e}(\zeta)}\theta \rightarrow \forall z(\texttt{h}(\zeta)\preccurlyeq z \\ &\prec \zeta \;\mathcal{J}(\texttt{Tr} f_z,y))))\big), \end{align*} $$
we obtain by the above-mentioned induction principle
 $$ \begin{align} \forall x & \prec \zeta \,\texttt{Prog}(\texttt{Tr} f_x)\rightarrow ( \forall y\prec \eta \,\texttt{Tr} f_{\zeta}(y)\rightarrow ( \theta\prec \varphi_{\texttt{e}(\zeta)}\eta\rightarrow \forall z(\texttt{h}(\zeta)\preccurlyeq z\nonumber \\ &\prec \zeta \;\mathcal{J}(\texttt{Tr} f_z,\theta)) )). \end{align} $$
$$ \begin{align} \forall x & \prec \zeta \,\texttt{Prog}(\texttt{Tr} f_x)\rightarrow ( \forall y\prec \eta \,\texttt{Tr} f_{\zeta}(y)\rightarrow ( \theta\prec \varphi_{\texttt{e}(\zeta)}\eta\rightarrow \forall z(\texttt{h}(\zeta)\preccurlyeq z\nonumber \\ &\prec \zeta \;\mathcal{J}(\texttt{Tr} f_z,\theta)) )). \end{align} $$
By the definition of progressiveness we obtain
Therefore, by combining the previous two claims, we obtain
 $$ \begin{align} \forall x\prec \zeta \,\texttt{Prog}(\texttt{Tr} f_x)\rightarrow \big(\forall y\prec \eta \,\texttt{Tr} f_{\zeta}(y)\rightarrow\forall z(\texttt{h}(\zeta)\preccurlyeq z \prec \zeta \;\mathcal{J} (\texttt{Tr} f_z,\varphi_{\texttt{e}(\zeta)}\eta))\big). \end{align} $$
$$ \begin{align} \forall x\prec \zeta \,\texttt{Prog}(\texttt{Tr} f_x)\rightarrow \big(\forall y\prec \eta \,\texttt{Tr} f_{\zeta}(y)\rightarrow\forall z(\texttt{h}(\zeta)\preccurlyeq z \prec \zeta \;\mathcal{J} (\texttt{Tr} f_z,\varphi_{\texttt{e}(\zeta)}\eta))\big). \end{align} $$
Finally, by Lemma 13 applied to (37), we can conclude that
 $$ \begin{align} \forall x\prec \zeta \,\texttt{Prog}(\texttt{Tr} f_x)\rightarrow \big(\forall y\prec \eta \,\texttt{Tr} f_{\zeta}(y)\rightarrow \texttt{Tr} f_{\zeta}(\eta))\big). \end{align} $$
$$ \begin{align} \forall x\prec \zeta \,\texttt{Prog}(\texttt{Tr} f_x)\rightarrow \big(\forall y\prec \eta \,\texttt{Tr} f_{\zeta}(y)\rightarrow \texttt{Tr} f_{\zeta}(\eta))\big). \end{align} $$
□
Let’s characterize the fundamental series of ordinals
![]() $<\Gamma _0$
as functions of natural numbers in the standard way:
$<\Gamma _0$
as functions of natural numbers in the standard way:
![]() $\gamma _0:=\omega $
, and
$\gamma _0:=\omega $
, and
![]() $\gamma _{n+1}:= \varphi _{\gamma _n}0$
. Then, we have:
$\gamma _{n+1}:= \varphi _{\gamma _n}0$
. Then, we have:
Proposition 4. If
![]() $\texttt {TI}_{\gamma _n} (P)$
is derivable in
$\texttt {TI}_{\gamma _n} (P)$
is derivable in
![]() $\textbf {KFL}^{*}$
, then
$\textbf {KFL}^{*}$
, then
 $\texttt {TI}_{\varphi _{\gamma _n} 0}(P)$
is derivable in
$\texttt {TI}_{\varphi _{\gamma _n} 0}(P)$
is derivable in
![]() $\textbf {KFL}^{*}$
.
$\textbf {KFL}^{*}$
.
Proof. We assume
![]() $\texttt {Prog}(P)$
. If
$\texttt {Prog}(P)$
. If
![]() $\texttt {TI}_{\gamma _n} (P)$
is derivable in
$\texttt {TI}_{\gamma _n} (P)$
is derivable in
![]() $\textbf {KFL}^{*}$
, then by Corollary 2 and the determinateness of P we can show
$\textbf {KFL}^{*}$
, then by Corollary 2 and the determinateness of P we can show
![]() $\texttt {TI}_{\omega ^{\gamma _n} +1} (P)$
. By the substitution rule we get that the hierarchy predicates are well-defined. Additionally we can prove that
$\texttt {TI}_{\omega ^{\gamma _n} +1} (P)$
. By the substitution rule we get that the hierarchy predicates are well-defined. Additionally we can prove that
Notice that by (39) we can reformulate this fragment of the hierarchy by replacing all the occurrences of the
![]() ${ \bf HYPE}$
-conditional by the material conditional. Therefore, we have
${ \bf HYPE}$
-conditional by the material conditional. Therefore, we have
 $$ \begin{align} \forall \zeta \prec \omega^{\gamma_n} +1 ( \texttt{Tr} f_{\zeta} (x) \leftrightarrow {\mathcal A} (\texttt{Tr} f^{\zeta}, \zeta,x) ). \end{align} $$
$$ \begin{align} \forall \zeta \prec \omega^{\gamma_n} +1 ( \texttt{Tr} f_{\zeta} (x) \leftrightarrow {\mathcal A} (\texttt{Tr} f^{\zeta}, \zeta,x) ). \end{align} $$
By the previous lemma, for
![]() $a\prec \omega ^{\gamma _n}+1$
,
$a\prec \omega ^{\gamma _n}+1$
,
and therefore, by the substitution rule applied to
![]() $\texttt {TI}_{\gamma _n} (P)$
and (41), we have that
$\texttt {TI}_{\gamma _n} (P)$
and (41), we have that
![]() $\texttt {Prog}(\texttt {Tr} f_{\omega ^{\gamma _n}})$
, which entails
$\texttt {Prog}(\texttt {Tr} f_{\omega ^{\gamma _n}})$
, which entails
![]() $\texttt {Tr} f_{\omega ^{\gamma _n}}({0})$
.
$\texttt {Tr} f_{\omega ^{\gamma _n}}({0})$
.
Using (40), we have
However, since
![]() $\texttt {h}(\omega ^{\gamma _n}) = 0$
and
$\texttt {h}(\omega ^{\gamma _n}) = 0$
and
![]() $\texttt {e}(\omega ^{\gamma _n}) = \gamma _n$
we can then infer
$\texttt {e}(\omega ^{\gamma _n}) = \gamma _n$
we can then infer
By letting
![]() $\zeta =y=0$
, we obtain
$\zeta =y=0$
, we obtain
![]() $\forall x\prec \varphi _{\texttt {e}(\omega ^{\gamma _n})}0\;P(x)$
, as desired.□
$\forall x\prec \varphi _{\texttt {e}(\omega ^{\gamma _n})}0\;P(x)$
, as desired.□
Corollary 7.
![]() $\textbf {KFL}^{*}$
defines the truth predicates of
$\textbf {KFL}^{*}$
defines the truth predicates of
![]() $\mathbf {RT}_{<\alpha }$
, for
$\mathbf {RT}_{<\alpha }$
, for
![]() $\alpha \prec \Gamma _0$
.
$\alpha \prec \Gamma _0$
.
Following the characterization of predicative analysis in terms of ramified systems given in [Reference Feferman2, Reference Feferman4], and the relationships between ramified truth and ramified analysis studied there, one can then conclude that the systems of ramified analysis below
![]() $\Gamma _0$
are proof-theoretically reducible to our system
$\Gamma _0$
are proof-theoretically reducible to our system
![]() $\textbf {KFL}^{*}$
.
$\textbf {KFL}^{*}$
.
In subsection 4.3 we showed that
![]() ${\textbf {KFL}}$
can be proof-theoretically reduced—w.r.t. arithmetical sentences—to
${\textbf {KFL}}$
can be proof-theoretically reduced—w.r.t. arithmetical sentences—to
![]() $\textbf {KF}$
. That argument can be lifted to
$\textbf {KF}$
. That argument can be lifted to
![]() $\textbf {KFL}^{*}$
. One can consider the system
$\textbf {KFL}^{*}$
. One can consider the system
![]() $\textbf {KF}^*$
—
$\textbf {KF}^*$
—
![]() $\texttt {Ref}^{*}(\texttt {PA}(P))$
in [Reference Feferman4]—and slightly modify the translations
$\texttt {Ref}^{*}(\texttt {PA}(P))$
in [Reference Feferman4]—and slightly modify the translations
![]() $\sigma $
,
$\sigma $
,
![]() $\tau $
from Definition 4: in particular, we let
$\tau $
from Definition 4: in particular, we let
Then, by induction on the length of proof in
![]() $\textbf {KFL}^{*}$
, we can prove:
$\textbf {KFL}^{*}$
, we can prove:
Proposition 5. If
![]() , then
, then
![]() .
.
Given the analysis of
![]() $\textbf {KF}^*$
given in [Reference Feferman4], the combination of Propositions 5 and 4 yields a sharp proof-theoretic analysis also for
$\textbf {KF}^*$
given in [Reference Feferman4], the combination of Propositions 5 and 4 yields a sharp proof-theoretic analysis also for
![]() $\textbf {KFL}^{*}$
:
$\textbf {KFL}^{*}$
:
Corollary 8.
![]() $|\textbf {KFL}^{*}|=|\textbf {KF}^*|=\Gamma _0$
.
$|\textbf {KFL}^{*}|=|\textbf {KF}^*|=\Gamma _0$
.
6 Laws of truth and intensionality
The main aim of the paper is to show that
![]() ${\textbf {KFL}}$
and
${\textbf {KFL}}$
and
![]() $\textbf {KFL}^{*}$
are proof-theoretically strong. We now conclude by discussing some of their philosophical virtues. We focus on
$\textbf {KFL}^{*}$
are proof-theoretically strong. We now conclude by discussing some of their philosophical virtues. We focus on
![]() ${\textbf {KFL}}$
, but our discussion transfers with little modification to
${\textbf {KFL}}$
, but our discussion transfers with little modification to
![]() $\textbf {KFL}^{*}$
. In particular, we now argue that
$\textbf {KFL}^{*}$
. In particular, we now argue that
![]() ${\textbf {KFL}}$
displays some advantages with respect to its direct competitors in classical logic (
${\textbf {KFL}}$
displays some advantages with respect to its direct competitors in classical logic (
![]() $\textbf {KF}$
) and nonclassical logic (
$\textbf {KF}$
) and nonclassical logic (
![]() $\textbf {PKF}$
).
$\textbf {PKF}$
).
Even truth theorists that consider classical logic as superior do not question the importance of the disquotational intuition for our philosophical notion of truth [Reference Feferman and Berger5, p. 189]. Theories such as
![]() $\textbf {KF}$
can only approximate such intuition, by restricting it to sentences that are ‘grounded’, in the sense of being provably true or false.
$\textbf {KF}$
can only approximate such intuition, by restricting it to sentences that are ‘grounded’, in the sense of being provably true or false.
![]() ${\textbf {KFL}}$
can preserve such intuition in great generality, by validating the
${\textbf {KFL}}$
can preserve such intuition in great generality, by validating the
![]() $\texttt {Tr}$
-schema for sentences not containing the conditional
$\texttt {Tr}$
-schema for sentences not containing the conditional
![]() $\rightarrow $
. Typically, however, nonclassical theories pay tribute to this greater vicinity to the unrestricted
$\rightarrow $
. Typically, however, nonclassical theories pay tribute to this greater vicinity to the unrestricted
![]() $\texttt {Tr}$
-schema (cf. Lemma 8) with a substantial loss in logical and deductive power. This is not so for
$\texttt {Tr}$
-schema (cf. Lemma 8) with a substantial loss in logical and deductive power. This is not so for
![]() ${\textbf {KFL}}$
: its proof-theoretic strength matches the one of
${\textbf {KFL}}$
: its proof-theoretic strength matches the one of
![]() $\textbf {KF}$
.
$\textbf {KF}$
.
![]() ${\textbf {KFL}}$
appears also to improve on the philosophical rationale behind the fully disquotational truth predicate of
${\textbf {KFL}}$
appears also to improve on the philosophical rationale behind the fully disquotational truth predicate of
![]() $\textbf {PKF}$
. Because of their missing conditional, all variants of
$\textbf {PKF}$
. Because of their missing conditional, all variants of
![]() $\textbf {PKF}$
do not have the means to express in the object language their basic principles of truth.
$\textbf {PKF}$
do not have the means to express in the object language their basic principles of truth.
![]() ${\textbf {KFL}}$
overcomes these limitations by replacing this metatheoretic inferential apparatus by truth theoretic laws formulated by means of the
${\textbf {KFL}}$
overcomes these limitations by replacing this metatheoretic inferential apparatus by truth theoretic laws formulated by means of the
![]() $\mathbf { HYPE}$
conditional. This also enables us to formulate fully in the language of
$\mathbf { HYPE}$
conditional. This also enables us to formulate fully in the language of
![]() ${\textbf {KFL}}$
principles of ‘mixed’ nature, such as induction principles open to the truth predicate or, in the case of
${\textbf {KFL}}$
principles of ‘mixed’ nature, such as induction principles open to the truth predicate or, in the case of
![]() $\textbf {KFL}^{*}$
, additional predicates. This is the root of the increased proof-theoretic strength of
$\textbf {KFL}^{*}$
, additional predicates. This is the root of the increased proof-theoretic strength of
![]() ${\textbf {KFL}}$
. As a consequence, we are also able to speak more fully about the truth (and falsity) of non-semantic sentences of
${\textbf {KFL}}$
. As a consequence, we are also able to speak more fully about the truth (and falsity) of non-semantic sentences of
![]() $\mathcal L_{\texttt {Tr}}^{\rightarrow }$
[Reference Leitgeb19, p. 391]: for instance, if compared to
$\mathcal L_{\texttt {Tr}}^{\rightarrow }$
[Reference Leitgeb19, p. 391]: for instance, if compared to
![]() $\textbf {PKF}$
,
$\textbf {PKF}$
,
![]() ${\textbf {KFL}}$
can prove many more iterations of the truth predicate over basic non-semantic truths such as
${\textbf {KFL}}$
can prove many more iterations of the truth predicate over basic non-semantic truths such as
![]() $0=0$
(Corollary 4).
$0=0$
(Corollary 4).
For a full philosophical defense of
![]() ${\textbf {KFL}}$
—which, however, is not the main aim of this paper—it is important to say something about the role of the conditional of
${\textbf {KFL}}$
—which, however, is not the main aim of this paper—it is important to say something about the role of the conditional of
![]() $\mathbf {HYPE}$
and its interaction with the truth predicate of
$\mathbf {HYPE}$
and its interaction with the truth predicate of
![]() ${\textbf {KFL}}$
. There are at least two ways of doing so. One could follow Leitgeb in providing a semantic explanation of the intensional nature of the
${\textbf {KFL}}$
. There are at least two ways of doing so. One could follow Leitgeb in providing a semantic explanation of the intensional nature of the
![]() $\mathbf {HYPE}$
conditional. According to Leitgeb, truth ascriptions are evaluated locally, at each fixed-point, whereas conditional statements are evaluated globally, that is, by looking at the entire structure of fixed points. Therefore, if the
$\mathbf {HYPE}$
conditional. According to Leitgeb, truth ascriptions are evaluated locally, at each fixed-point, whereas conditional statements are evaluated globally, that is, by looking at the entire structure of fixed points. Therefore, if the
![]() $\texttt {Tr}$
-schema held also for conditional claims, a truth ascription that contains the conditional would need to be evaluated both locally and globally, which would amount to a category mistake in
$\texttt {Tr}$
-schema held also for conditional claims, a truth ascription that contains the conditional would need to be evaluated both locally and globally, which would amount to a category mistake in
![]() $\mathfrak {M}_{\Phi }$
.
$\mathfrak {M}_{\Phi }$
.
Alternatively, one could attempt a direct proof-theoretic explanation of the interaction of the truth predicate and the
![]() $\mathbf {HYPE}$
-conditional. Leon Horsten [Reference Horsten16] defends
$\mathbf {HYPE}$
-conditional. Leon Horsten [Reference Horsten16] defends
![]() $\textbf {PKF}$
on the basis of inferential deflationism: the basic principles of disquotational truth are given inferentially, and essentially so [Reference Horsten16, sec. 10.2]. Horsten claims in particular that the laws of truth can only be expressed against the background of an inferential apparatus which is not part of the language to which truth is applied. One might extend Horsten’s inferential approach to the present case, and argue that
$\textbf {PKF}$
on the basis of inferential deflationism: the basic principles of disquotational truth are given inferentially, and essentially so [Reference Horsten16, sec. 10.2]. Horsten claims in particular that the laws of truth can only be expressed against the background of an inferential apparatus which is not part of the language to which truth is applied. One might extend Horsten’s inferential approach to the present case, and argue that
![]() ${\textbf {KFL}}$
characterizes truth in a similar fashion. The laws of truth are given against the background of a theoretical apparatus that essentially involves the conditional of
${\textbf {KFL}}$
characterizes truth in a similar fashion. The laws of truth are given against the background of a theoretical apparatus that essentially involves the conditional of
![]() $\mathbf {HYPE}$
. Such theoretical apparatus amounts to the inferential structure of the truth laws of
$\mathbf {HYPE}$
. Such theoretical apparatus amounts to the inferential structure of the truth laws of
![]() $\textbf {PKF}$
, but now formulated in the language of our theory of truth. This would also explain why the
$\textbf {PKF}$
, but now formulated in the language of our theory of truth. This would also explain why the
![]() $\texttt {Tr}$
-schema only holds for sentences that do not contain the
$\texttt {Tr}$
-schema only holds for sentences that do not contain the
![]() $\mathbf {HYPE}$
-conditional. On this picture, one should not expect the conditional of
$\mathbf {HYPE}$
-conditional. On this picture, one should not expect the conditional of
![]() $\mathbf {HYPE}$
to appear in truth ascriptions in
$\mathbf {HYPE}$
to appear in truth ascriptions in
![]() ${\textbf {KFL}}$
, in the same way as one should not expect inferential devices of
${\textbf {KFL}}$
, in the same way as one should not expect inferential devices of
![]() $\textbf {PKF}$
(such as sequent arrows) to appear under the scope of its truth predicate.
$\textbf {PKF}$
(such as sequent arrows) to appear under the scope of its truth predicate.
As mentioned, a full philosophical defense of
![]() ${\textbf {KFL}}$
is outside the scope of our paper, and it will be carried out in future work.
${\textbf {KFL}}$
is outside the scope of our paper, and it will be carried out in future work.
Acknowledgments
The authors would like to thank Rosalie Iemhoff and Hannes Leitgeb for helpful discussion on topics treated in the paper, and Stanislav Speranski for the permission to cite his unpublished work. Martin Fischer would like to thank the audience of the FSB-seminar in Bristol. His project was funded by the DFG: “Gefördert durch die Deutsche Forschungsgemeinschaft (DFG)—Projektnummer 407312485.” Pablo Dopico’s research was partially funded by a King’s College London Undergraduate Research Fellowship (KURF) under the supervision of Carlo Nicolai. Special thanks go to Maria Beatrice Buonaguidi and Boaz Laan, who actively contributed to the KURF project.









