No topic which we have discussed approaches closer to the problem of a uniform and universal language in mathematics than does the topic of symbolic logic. The problem of efficient and uniform notations is perhaps the most serious one facing the mathematical public. No group of workers has been more active in the endeavor to find a solution of that problem than those who have busied themselves with symbolic logic … Each proposed a list of symbols, with the hope, no doubt, that mathematicians in general would adopt them. That expectation has not been realized.
Cajori (Reference Cajori1929, p. 314)1 The mystery of ‘
 $\boldsymbol \vee $
’
$\boldsymbol \vee $
’
The symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for inclusive disjunction is almost universally accepted. This contrasts with every other logical operator: negation is symbolized by ‘
$\mathbin {\boldsymbol {\vee }}$
’ for inclusive disjunction is almost universally accepted. This contrasts with every other logical operator: negation is symbolized by ‘
![]() $\mathord {\boldsymbol {\neg }}$
’, ‘
$\mathord {\boldsymbol {\neg }}$
’, ‘
![]() $\mathord {\boldsymbol {\sim }}$
’, ‘
$\mathord {\boldsymbol {\sim }}$
’, ‘
![]() $\boldsymbol {-}$
’, or an overline, conjunction is symbolized by ‘
$\boldsymbol {-}$
’, or an overline, conjunction is symbolized by ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’, ‘
$\mathbin {\boldsymbol {\wedge }}$
’, ‘
![]() $\&$
’, and ‘
$\&$
’, and ‘
![]() ’, and (material) implication is symbolized by ‘
’, and (material) implication is symbolized by ‘
![]() $\boldsymbol {\rightarrow }$
’ and ‘
$\boldsymbol {\rightarrow }$
’ and ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’. So where do we get ‘
$\mathbin {\boldsymbol {\supset }}$
’. So where do we get ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ from and why have logicians more or less settled on this one symbol? We answer this question here and show that we get the ubiquitous ‘
$\mathbin {\boldsymbol {\vee }}$
’ from and why have logicians more or less settled on this one symbol? We answer this question here and show that we get the ubiquitous ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction from Whitehead and Russell’s pre-Principia work in formal logic.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction from Whitehead and Russell’s pre-Principia work in formal logic.
Our answer to this question differs from that given by earlier studies of formal logic and its notations. The earliest use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction recorded in the encyclopedic list given by Cajori (Reference Cajori1929, p. 307) is in Whitehead and Russell’s 1910 Principia. The Kneales say that “the system [which includes ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction recorded in the encyclopedic list given by Cajori (Reference Cajori1929, p. 307) is in Whitehead and Russell’s 1910 Principia. The Kneales say that “the system [which includes ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’] is that introduced by Peano in his Notations de logique mathématique of 1894, developed in the successive editions of his Formulaire de mathématiques, and then perfected by Whitehead and Russell in their Principia Mathematica of 1910” (Kneale & Kneale, Reference Kneale and Kneale1962, p. 520). In fact, however, Peano always used ‘
$\mathbin {\boldsymbol {\vee }}$
’] is that introduced by Peano in his Notations de logique mathématique of 1894, developed in the successive editions of his Formulaire de mathématiques, and then perfected by Whitehead and Russell in their Principia Mathematica of 1910” (Kneale & Kneale, Reference Kneale and Kneale1962, p. 520). In fact, however, Peano always used ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ for inclusive disjunction and did not use ‘
$\mathrel {\boldsymbol {\cup }}$
’ for inclusive disjunction and did not use ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ at all. So one might suspect that the symbol for disjunction is one of the improvements introduced by Whitehead and Russell in Principia Mathematica. But is that true? Why was ‘
$\mathbin {\boldsymbol {\vee }}$
’ at all. So one might suspect that the symbol for disjunction is one of the improvements introduced by Whitehead and Russell in Principia Mathematica. But is that true? Why was ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ chosen specifically? And why was it then universally adopted even as logicians introduced alternatives for all of Principia’s other logical symbols?
$\mathbin {\boldsymbol {\vee }}$
’ chosen specifically? And why was it then universally adopted even as logicians introduced alternatives for all of Principia’s other logical symbols?
The story has two parts: The first part concerns the introduction of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ by Whitehead and Russell, who were working within the notational and formal logical tradition of Peano. We suggest here that the initial introduction of ‘
$\mathbin {\boldsymbol {\vee }}$
’ by Whitehead and Russell, who were working within the notational and formal logical tradition of Peano. We suggest here that the initial introduction of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ was motivated by a shared commitment to two design principles for logical symbolisms (Schlimm, Reference Schlimm2018, Reference Schlimm2021; Toader, Reference Toader2021).Footnote
1
The first principle is that symbols should be unambiguous—one shouldn’t use the same symbol in different meanings. The second principle is that analogous notions—better, notions satisfying analogous logical laws (say, associativity)—should get similar symbols: similar notions should have a similar, though not identical, notation.Footnote
2
$\mathbin {\boldsymbol {\vee }}$
’ was motivated by a shared commitment to two design principles for logical symbolisms (Schlimm, Reference Schlimm2018, Reference Schlimm2021; Toader, Reference Toader2021).Footnote
1
The first principle is that symbols should be unambiguous—one shouldn’t use the same symbol in different meanings. The second principle is that analogous notions—better, notions satisfying analogous logical laws (say, associativity)—should get similar symbols: similar notions should have a similar, though not identical, notation.Footnote
2
As we suggest below, this first design principle led Peano to adopt a new symbol, namely ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’, to indicate a kind of logical union or addition, and to avoid the then-prevalent symbol ‘
$\mathrel {\boldsymbol {\cup }}$
’, to indicate a kind of logical union or addition, and to avoid the then-prevalent symbol ‘
![]() $+$
’ for this use. The point of this was to distinguish arithmetic and logical addition. Russell followed Peano’s practice here, as we will see below.Footnote
3
Subsequently, in the early logical investigations which ultimately led to Principia, Russell introduced the symbol ‘
$+$
’ for this use. The point of this was to distinguish arithmetic and logical addition. Russell followed Peano’s practice here, as we will see below.Footnote
3
Subsequently, in the early logical investigations which ultimately led to Principia, Russell introduced the symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ motivated by that same design principle that Peano held: Russell wanted to distinguish notationally between two kinds of logical addition, namely, propositional disjunction (a.k.a. “propositional addition”) and class union (a.k.a. “class addition”). In this, Russell out-Peanoed Peano, who used ‘
$\mathbin {\boldsymbol {\vee }}$
’ motivated by that same design principle that Peano held: Russell wanted to distinguish notationally between two kinds of logical addition, namely, propositional disjunction (a.k.a. “propositional addition”) and class union (a.k.a. “class addition”). In this, Russell out-Peanoed Peano, who used ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ for both.Footnote
4
But Russell followed the second design principle, that analogous notions should have similar symbols, in adopting ‘
$\mathrel {\boldsymbol {\cup }}$
’ for both.Footnote
4
But Russell followed the second design principle, that analogous notions should have similar symbols, in adopting ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ as a sharpening of ‘
$\mathbin {\boldsymbol {\vee }}$
’ as a sharpening of ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ so as to stress the analogy between propositional sum and class union. Russell did not think that this analogy was perfect. He held that the formal laws for propositional addition and class addition differed; hence he felt a need for a different, yet similar, symbol.Footnote
5
But even where the formal laws are identical, Russell wanted to mark the distinction between operations on different terms, as in the case of class union and relation union. This pattern is noticeable in, for instance, Russell’s development of many symbols of his logic of relations, which are usually distinguished only by an accenting mark, suggesting that Russell tacitly followed the second design principle, albeit a weaker version of it than Peano apparently endorsed.
$\mathrel {\boldsymbol {\cup }}$
’ so as to stress the analogy between propositional sum and class union. Russell did not think that this analogy was perfect. He held that the formal laws for propositional addition and class addition differed; hence he felt a need for a different, yet similar, symbol.Footnote
5
But even where the formal laws are identical, Russell wanted to mark the distinction between operations on different terms, as in the case of class union and relation union. This pattern is noticeable in, for instance, Russell’s development of many symbols of his logic of relations, which are usually distinguished only by an accenting mark, suggesting that Russell tacitly followed the second design principle, albeit a weaker version of it than Peano apparently endorsed.
All of that is the first part of the story. The second part of the story is that of the adoption of
![]() $\mathbin {\boldsymbol {\vee }}$
in the period after Principia, when a number of logical symbolisms (and indeed, logical methodologies) were in use simultaneously. The main rivals of Principia were the algebraic approach of the tradition of Boole, Peirce, and Schröder, and the axiomatic logic of Hilbert, with their respective notations. Despite being heavily influenced by both Principia and the algebraic notation of Schröder (which goes back to Peirce and the Boolean school), Hilbert introduced different symbols for all the logical connectives—except disjunction.
$\mathbin {\boldsymbol {\vee }}$
in the period after Principia, when a number of logical symbolisms (and indeed, logical methodologies) were in use simultaneously. The main rivals of Principia were the algebraic approach of the tradition of Boole, Peirce, and Schröder, and the axiomatic logic of Hilbert, with their respective notations. Despite being heavily influenced by both Principia and the algebraic notation of Schröder (which goes back to Peirce and the Boolean school), Hilbert introduced different symbols for all the logical connectives—except disjunction.
One upshot of the above findings is to uproot a misconception about the origins of the modern symbol for disjunction. A common story in textbooks is that
![]() $\mathbin {\boldsymbol {\vee }}$
really is a version of the letter ‘v’, the initial letter of vel, the Latin word for “or.” We wanted to find out whether this was a typographical accident, and later writers simply thought the similarity between ‘
$\mathbin {\boldsymbol {\vee }}$
really is a version of the letter ‘v’, the initial letter of vel, the Latin word for “or.” We wanted to find out whether this was a typographical accident, and later writers simply thought the similarity between ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ and the initial of vel should be suggested as a mnemonic device to students, or whether it actually played a role in the choice of the symbol. Here we argue that although there is a single use of ‘v’ as a logical symbol abbreviating vel in Leibniz, this played no known role in Peano’s choice or in Whitehead and Russell’s choice of notation for disjunction. However, this historical connection may, at least in part, have lead Hilbert to adopt it.
$\mathbin {\boldsymbol {\vee }}$
’ and the initial of vel should be suggested as a mnemonic device to students, or whether it actually played a role in the choice of the symbol. Here we argue that although there is a single use of ‘v’ as a logical symbol abbreviating vel in Leibniz, this played no known role in Peano’s choice or in Whitehead and Russell’s choice of notation for disjunction. However, this historical connection may, at least in part, have lead Hilbert to adopt it.
As usual in the history of mathematics, there is no simple answer to the question of who deserves credit for ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’. In one sense, it can be answered simply by recording the earliest use of the symbol. But the earliest occurrence is often not the use to which the current practice of the use of the symbol is historically connected. For instance, Peirce in fact used ‘
$\mathbin {\boldsymbol {\vee }}$
’. In one sense, it can be answered simply by recording the earliest use of the symbol. But the earliest occurrence is often not the use to which the current practice of the use of the symbol is historically connected. For instance, Peirce in fact used ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction before Whitehead or Russell did—but this use was independent and played no role in the historical development of logical notation systems. (In this case we know this for a fact because Peirce’s relevant writings were not published until long after the use of ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction before Whitehead or Russell did—but this use was independent and played no role in the historical development of logical notation systems. (In this case we know this for a fact because Peirce’s relevant writings were not published until long after the use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ was already entrenched, in 1933.) So it is only by tracing the adoption of Russell’s symbol that we can establish Russell as the originator of “our” ‘
$\mathbin {\boldsymbol {\vee }}$
’ was already entrenched, in 1933.) So it is only by tracing the adoption of Russell’s symbol that we can establish Russell as the originator of “our” ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’.
$\mathbin {\boldsymbol {\vee }}$
’.
There is a related question, namely that of what should count as a symbol for propositional disjunction in the first place. Is Peano’s ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ a symbol for disjunction, or is it a symbol for something else, perhaps an ambiguous combination of disjunction and union? Who invented disjunction in the sense we now use it—as a connective between truth-apt expressions? This is certainly a deeper and more interesting question, but one we cannot answer here. Our contribution is more modest: to trace the history of the symbol ‘
$\mathrel {\boldsymbol {\cup }}$
’ a symbol for disjunction, or is it a symbol for something else, perhaps an ambiguous combination of disjunction and union? Who invented disjunction in the sense we now use it—as a connective between truth-apt expressions? This is certainly a deeper and more interesting question, but one we cannot answer here. Our contribution is more modest: to trace the history of the symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ only, and not the concept it expresses.Footnote
6
We do this not by merely recording its first use, but by placing it in the context of the development of logical symbolisms. Of course, even this is a much larger context which we cannot do justice here—we focus only on the parts that are relevant to ‘
$\mathbin {\boldsymbol {\vee }}$
’ only, and not the concept it expresses.Footnote
6
We do this not by merely recording its first use, but by placing it in the context of the development of logical symbolisms. Of course, even this is a much larger context which we cannot do justice here—we focus only on the parts that are relevant to ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’.
$\mathbin {\boldsymbol {\vee }}$
’.
Both of these considerations lead us to reject the claim that Leibniz’s use of ‘v’ should be considered the origin of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’. As we will show, (a) it had no known influence on the eventual introduction and development of ‘
$\mathbin {\boldsymbol {\vee }}$
’. As we will show, (a) it had no known influence on the eventual introduction and development of ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ and ‘
$\mathrel {\boldsymbol {\cup }}$
’ and ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ by Peano, Whitehead, or Russell, and (b) Leibniz’s ‘v’ was not a symbol for propositional disjunction.
$\mathbin {\boldsymbol {\vee }}$
’ by Peano, Whitehead, or Russell, and (b) Leibniz’s ‘v’ was not a symbol for propositional disjunction.
We settle the questions of who invented the use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction (Whitehead or Russell) and whether this use of ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction (Whitehead or Russell) and whether this use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ was in fact introduced as an abbreviation for vel (it was not). We suggest, however, that even though these questions may seem trivial, they are not uninteresting, and we will mention, along the way, other interesting aspects of the development of logical symbolism. Further, the story serves as a case study in how the choice and adoption of symbols and the organization of a symbolic system (a kind of conceptual framework) can be determined by methodological commitments but also by extrinsic factors such as the availability or cost of printer’s type or the influence that textbooks have on the adoption of symbolisms. In this instance, in addition to the commitment to unambiguous notations in Peano and Russell mentioned above, another factor concerns the reasons that led Russell to choose disjunction as a primitive of the logical system of Principia.
$\mathbin {\boldsymbol {\vee }}$
’ was in fact introduced as an abbreviation for vel (it was not). We suggest, however, that even though these questions may seem trivial, they are not uninteresting, and we will mention, along the way, other interesting aspects of the development of logical symbolism. Further, the story serves as a case study in how the choice and adoption of symbols and the organization of a symbolic system (a kind of conceptual framework) can be determined by methodological commitments but also by extrinsic factors such as the availability or cost of printer’s type or the influence that textbooks have on the adoption of symbolisms. In this instance, in addition to the commitment to unambiguous notations in Peano and Russell mentioned above, another factor concerns the reasons that led Russell to choose disjunction as a primitive of the logical system of Principia.
2 Leibniz
Leibniz deserves some credit for the first use of ‘v’ as a symbol for ‘or’ in some sense.Footnote 7 But Leibniz’s use of ‘v’ is not for propositional disjunction, and occurs in only one manuscript, his 1679 “Matheseos universalis pars prior: De terminis incomplexis” (Figure 1):
Also, in the way that
![]() $+$
is a conjunctive mark or sign of aggregation corresponding to the word and—as in
$+$
is a conjunctive mark or sign of aggregation corresponding to the word and—as in
![]() $a + b$
, that is, a and b together—so a disjunctive mark or sign of alternation is also given, which corresponds to the word or [vel], so
$a + b$
, that is, a and b together—so a disjunctive mark or sign of alternation is also given, which corresponds to the word or [vel], so
![]() signifies a or b to me. It also has a use in calculus, for if we have
signifies a or b to me. It also has a use in calculus, for if we have
![]() $xx + ab = \overline {a + b}x$
, then x will be equal to
$xx + ab = \overline {a + b}x$
, then x will be equal to
![]() , whether it signifies a or whether it signifies b. In this respect it will have an ambiguous value. For example, if
, whether it signifies a or whether it signifies b. In this respect it will have an ambiguous value. For example, if
![]() $xx + 6 = 5x$
, x can be
$xx + 6 = 5x$
, x can be
![]() $2$
, but x can also be
$2$
, but x can also be
![]() $3$
. For if x is
$3$
. For if x is
![]() $2$
, then from
$2$
, then from
![]() $xx + 6 = 5x$
, we get
$xx + 6 = 5x$
, we get
![]() $4 + 6 = 10$
; and if x is
$4 + 6 = 10$
; and if x is
![]() $3$
, then from
$3$
, then from
![]() $xx = 6 = 5x$
, we get
$xx = 6 = 5x$
, we get
![]() $9 + 6 = 15$
. However, many values of this unknown [variable] or of the present equation cannot be given roots, as will be clear in the appropriate place below.
$9 + 6 = 15$
. However, many values of this unknown [variable] or of the present equation cannot be given roots, as will be clear in the appropriate place below.

Fig. 1 Use of
![]() in Leibniz Reference Leibniz1679).
in Leibniz Reference Leibniz1679).
Hence, ambiguous signs also have a use, and this will be clear in the appropriate place below, ambiguity being the font of irrationality in calculus; and so when I write
![]() $x = 3 + \sqrt 4$
, this can be explicated by
$x = 3 + \sqrt 4$
, this can be explicated by
![]() $3 + \sqrt 4$
or
$3 + \sqrt 4$
or
![]() $3 + 2$
or
$3 + 2$
or
![]() $5$
, just as when I write
$5$
, just as when I write
![]() $3 - \sqrt 4$
, it is explicated either by
$3 - \sqrt 4$
, it is explicated either by
![]() $3 - 2$
or
$3 - 2$
or
![]() $1$
; thus, we get
$1$
; thus, we get
![]() . For in order for us to remove the irrationality, let
. For in order for us to remove the irrationality, let
![]() $x - 3 = \sqrt 4$
; therefore
$x - 3 = \sqrt 4$
; therefore
![]() $xx - 6x + 9 = 4$
, whether
$xx - 6x + 9 = 4$
, whether
![]() $xx - 6x + 5 = 0$
or
$xx - 6x + 5 = 0$
or
![]() $xx + 5 = 6x$
, where it is clear that it would satisfy
$xx + 5 = 6x$
, where it is clear that it would satisfy
![]() $5$
as much as
$5$
as much as
![]() $1$
. For if x were given the value
$1$
. For if x were given the value
![]() $5$
, we would get
$5$
, we would get
![]() $25 + 5 = 30$
; if x is given the value
$25 + 5 = 30$
; if x is given the value
![]() $1$
, we get
$1$
, we get
![]() $1 + 5 = 6$
.Footnote
8
$1 + 5 = 6$
.Footnote
8
This occurrence of ‘
![]() ’ is the first use of a ‘
’ is the first use of a ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’-like symbol for ‘or’ (in some sense) that we know of.Footnote
9
However, Leibniz does not seem to use the symbol here as a sign for disjunction of (truth-apt) propositions as is usually the case today. Indeed, the surrounding context does not include any uses of ‘a’ or ‘b’ for propositions. Rather, Leibniz seems to be using ‘a’ and ‘b’ here as standing for (truth-inapt) terms, and using ‘
$\mathbin {\boldsymbol {\vee }}$
’-like symbol for ‘or’ (in some sense) that we know of.Footnote
9
However, Leibniz does not seem to use the symbol here as a sign for disjunction of (truth-apt) propositions as is usually the case today. Indeed, the surrounding context does not include any uses of ‘a’ or ‘b’ for propositions. Rather, Leibniz seems to be using ‘a’ and ‘b’ here as standing for (truth-inapt) terms, and using ‘
![]() ’ to indicate ambiguity, that is, one of two alternatives without a specific one being indicated, as in phrases like “either chocolate or vanilla” or “7 or 8.”Footnote
10
That use of ‘
’ to indicate ambiguity, that is, one of two alternatives without a specific one being indicated, as in phrases like “either chocolate or vanilla” or “7 or 8.”Footnote
10
That use of ‘
![]() ’ for alternation between truth-inapt terms is consistent with the other two uses ‘
’ for alternation between truth-inapt terms is consistent with the other two uses ‘
![]() ’ and ‘
’ and ‘
![]() ’, where the symbol is flanked by (variables for) numbers and serves to produce an ambiguously referring term.Footnote
11
’, where the symbol is flanked by (variables for) numbers and serves to produce an ambiguously referring term.Footnote
11
These three uses, in this one manuscript, seem to be the only uses of the symbol ‘
![]() ’ in the entirety of his Mathematische Schriften (Leibniz, Reference Leibniz1863). We also found it nowhere else in Leibniz’s writings. So this manuscript may record the only uses of ‘
’ in the entirety of his Mathematische Schriften (Leibniz, Reference Leibniz1863). We also found it nowhere else in Leibniz’s writings. So this manuscript may record the only uses of ‘
![]() ’ for alternation of (truth-inapt) terms in Leibniz’s corpus. The manuscript was not edited or published until 1863. It is perhaps unsurprising, then, that Leibniz’s use of ‘
’ for alternation of (truth-inapt) terms in Leibniz’s corpus. The manuscript was not edited or published until 1863. It is perhaps unsurprising, then, that Leibniz’s use of ‘
![]() ’ for disjunction (which, so far as we can tell, was confined to this one manuscript) found no imitators: even Arnauld’s (Reference Arnauld1683) La logique ou l’art de penser, which was an especially influential book in the 1700s and in the 1800s before Boole’s work, omits ‘v’ for disjunction. Logicians in the 1700s and 1800s largely used symbols, when they did at all, for the relations between terms in categorical logic and not propositional disjunction; indeed, most logicians either did not symbolize propositional disjunction and argued it was eliminable as a form of reasoning, or else did not discuss it all (see Hailperin, Reference Hailperin, Gabbay and Woods2004, p. 339, for discussion).Footnote
12
’ for disjunction (which, so far as we can tell, was confined to this one manuscript) found no imitators: even Arnauld’s (Reference Arnauld1683) La logique ou l’art de penser, which was an especially influential book in the 1700s and in the 1800s before Boole’s work, omits ‘v’ for disjunction. Logicians in the 1700s and 1800s largely used symbols, when they did at all, for the relations between terms in categorical logic and not propositional disjunction; indeed, most logicians either did not symbolize propositional disjunction and argued it was eliminable as a form of reasoning, or else did not discuss it all (see Hailperin, Reference Hailperin, Gabbay and Woods2004, p. 339, for discussion).Footnote
12
To qualify this slightly, a close textual reading of one or another figure may extract, induce, or produce a propositional logic in some sense.Footnote
13
Even so, our interest lies in the story of how ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ became so widespread as a symbol for disjunction in modern usage. It is our contention that Leibniz and other logicians working primarily with categorical logics—between Leibniz and Boole, we might say—did not inspire or cause the usage that we now have today.
$\mathbin {\boldsymbol {\vee }}$
’ became so widespread as a symbol for disjunction in modern usage. It is our contention that Leibniz and other logicians working primarily with categorical logics—between Leibniz and Boole, we might say—did not inspire or cause the usage that we now have today.
3 The nineteenth century
In the course of mathematically analyzing logical principles using algebraic equations, Boole used ‘
![]() $+$
’ as a symbol for something akin to ‘
$+$
’ as a symbol for something akin to ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’. In Boole’s algebra, however, ‘
$\mathbin {\boldsymbol {\vee }}$
’. In Boole’s algebra, however, ‘
![]() $+$
’ is not a symbol for disjunction in our sense, since the expressions that flank ‘
$+$
’ is not a symbol for disjunction in our sense, since the expressions that flank ‘
![]() $+$
’ are not signs for propositions or statements, but for concept expressions,Footnote
14
and so has rightly been thought of as an algebra of classes (as we might put it), or as an algebra of concepts in extension (as Boole seems to put it).
$+$
’ are not signs for propositions or statements, but for concept expressions,Footnote
14
and so has rightly been thought of as an algebra of classes (as we might put it), or as an algebra of concepts in extension (as Boole seems to put it).
Boole can appropriately use ‘
![]() $1$
’ for the universe, multiplication for class intersection, and subtraction for complementation (Boole, Reference Boole1847, p. 20). Although Boole’s operators ‘
$1$
’ for the universe, multiplication for class intersection, and subtraction for complementation (Boole, Reference Boole1847, p. 20). Although Boole’s operators ‘
![]() $+$
’ and ‘
$+$
’ and ‘
![]() $\cdot $
’ applied primarily to classes, he also considered symbols ‘x’ for propositions as expressing the “cases” where the proposition X in question is true. The expression ‘
$\cdot $
’ applied primarily to classes, he also considered symbols ‘x’ for propositions as expressing the “cases” where the proposition X in question is true. The expression ‘
![]() $x+y$
’ then expresses the union of the cases where X and Y are true—assuming, however, that these classes are disjoint. Claims about the propositions are made using equations involving
$x+y$
’ then expresses the union of the cases where X and Y are true—assuming, however, that these classes are disjoint. Claims about the propositions are made using equations involving
![]() $1$
and
$1$
and
![]() $0$
(the empty class). Multiplication is re-interpreted to define (the algebraic analogue of) propositional conjunction; similarly subtraction is re-interpreted as (the algebraic analogue of) propositional negation. Then these operations so-interpreted are similarly used to define (the algebraic analogues of) propositional implication and propositional disjunction. In Boole’s system, that either X is true or Y is true would be expressed using the equation
$0$
(the empty class). Multiplication is re-interpreted to define (the algebraic analogue of) propositional conjunction; similarly subtraction is re-interpreted as (the algebraic analogue of) propositional negation. Then these operations so-interpreted are similarly used to define (the algebraic analogues of) propositional implication and propositional disjunction. In Boole’s system, that either X is true or Y is true would be expressed using the equation
![]() $x+y-xy=1$
(Boole, Reference Boole1847, p. 51).
$x+y-xy=1$
(Boole, Reference Boole1847, p. 51).
Of course, Boole’s choice of ‘
![]() $+$
’ for disjunction (Boole, Reference Boole1847, Reference Boole1854) had a more immediate influence on notation for disjunction in the 1800s.Footnote
15
Subsequent choices of symbols for operations on classes were influenced by Boole even when logicians departed from Boole’s philosophical program to varying degrees. For example, Jevons (Reference Jevons1883) uses ‘
$+$
’ for disjunction (Boole, Reference Boole1847, Reference Boole1854) had a more immediate influence on notation for disjunction in the 1800s.Footnote
15
Subsequent choices of symbols for operations on classes were influenced by Boole even when logicians departed from Boole’s philosophical program to varying degrees. For example, Jevons (Reference Jevons1883) uses ‘
![]() $\cdot |\cdot $
’ for non-disjoint union, to distinguish it from Boole’s ‘
$\cdot |\cdot $
’ for non-disjoint union, to distinguish it from Boole’s ‘
![]() $+$
’.Footnote
16
Peirce (Reference Peirce1870, p. 9) similarly uses ‘
$+$
’.Footnote
16
Peirce (Reference Peirce1870, p. 9) similarly uses ‘
![]() $+$
’ for disjoint union and adopts ‘
$+$
’ for disjoint union and adopts ‘
![]() $\mathbin {+\mkern -2mu,}$
’ for non-disjoint union.Footnote
17
In “The Simplest Mathematics” (Reference Peirce1902), which was not published until 1933, Peirce actually used ‘
$\mathbin {+\mkern -2mu,}$
’ for non-disjoint union.Footnote
17
In “The Simplest Mathematics” (Reference Peirce1902), which was not published until 1933, Peirce actually used ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ interchangeably with his ‘
$\mathbin {\boldsymbol {\vee }}$
’ interchangeably with his ‘
![]() ’ symbol for inclusive or. By 1933, of course, the use of ‘
’ symbol for inclusive or. By 1933, of course, the use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction was already entrenched. Other important writers on the algebra of logic, such as Schröder (Reference Schröder1877, Reference Schröder1890), MacColl (Reference McColl1877), and Ladd-Franklin (Reference Ladd and Peirce1883), all use ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction was already entrenched. Other important writers on the algebra of logic, such as Schröder (Reference Schröder1877, Reference Schröder1890), MacColl (Reference McColl1877), and Ladd-Franklin (Reference Ladd and Peirce1883), all use ‘
![]() $+$
’ for union, and so does Whitehead (Reference Whitehead1898) originally. Even Nagy (Reference Nagy1890), writing in Italian and familiar with Peano’s work, sticks to Boole’s notation.
$+$
’ for union, and so does Whitehead (Reference Whitehead1898) originally. Even Nagy (Reference Nagy1890), writing in Italian and familiar with Peano’s work, sticks to Boole’s notation.
Common to the followers of Boole is not just the choice of symbols, but also the exclusive focus on equations. Using equations, they express relations between class terms, and provide translations of syllogistic reasoning into such equations. However, MacColl (Reference McColl1877), Peirce (Reference Peirce1885), Ladd-Franklin (Reference Ladd and Peirce1883), and Schröder (Reference Schröder1891) took the further step of showing that terms could translate propositionally valid inferential relationships. They allowed operators like ‘
![]() $+$
’ to connect not just terms for classes or concepts but also terms for propositions or statements, and developed systems of formulas, not just of equations. In their work, the symbol ‘
$+$
’ to connect not just terms for classes or concepts but also terms for propositions or statements, and developed systems of formulas, not just of equations. In their work, the symbol ‘
![]() $+$
’ serves as a genuine propositional disjunction (in the inclusive sense).Footnote
18
$+$
’ serves as a genuine propositional disjunction (in the inclusive sense).Footnote
18
Working alongside the algebraic logicians were Frege and Peano, who both were important sources for Russell. Frege had his own two-dimensional notation (first introduced in Begriffsschrift and later developed in Grundgesetze). He was able to define disjunction using the content strokes for implication and negation, but did not introduce a separate symbol for it (Frege, Reference Frege1879, p. 11). Regarding Frege’s notational influence on the story of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’, the record shows that Frege’s actual notations and two-dimensional style were rarely adopted (and sometimes were ignored or even maligned) by others (with the exception of his popular turnstile ‘
$\mathbin {\boldsymbol {\vee }}$
’, the record shows that Frege’s actual notations and two-dimensional style were rarely adopted (and sometimes were ignored or even maligned) by others (with the exception of his popular turnstile ‘
![]() ’). But Frege’s notational influence on Russell was nonetheless felt: indeed, Frege’s views on design principles for notation seem to have been quite influential on Russell, even though his choice of actual symbols was not. Russell’s engagement with Frege’s writings seems to have led Russell to later distinguish propositional sum and class sum, for which purpose he introduced our ‘
’). But Frege’s notational influence on Russell was nonetheless felt: indeed, Frege’s views on design principles for notation seem to have been quite influential on Russell, even though his choice of actual symbols was not. Russell’s engagement with Frege’s writings seems to have led Russell to later distinguish propositional sum and class sum, for which purpose he introduced our ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’—as we will see. First, however, we consider the influence of Peano’s notations and logical framework on the development of Principia.
$\mathbin {\boldsymbol {\vee }}$
’—as we will see. First, however, we consider the influence of Peano’s notations and logical framework on the development of Principia.
4 Peano
Peano is responsible for much of the notations in Principia, and Russell’s notational imitations of Peano likely led him to introduce ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction. Indeed, Peano seems to be responsible for suggesting to later readers that ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction. Indeed, Peano seems to be responsible for suggesting to later readers that ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ was a sensible (Latin-inspired) choice of symbol for disjunction.
$\mathbin {\boldsymbol {\vee }}$
’ was a sensible (Latin-inspired) choice of symbol for disjunction.
Peano, however, did not use ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ (or the letter ‘v’) for disjunction or class union. From his Calcolo geometrico onward, he instead used ‘
$\mathbin {\boldsymbol {\vee }}$
’ (or the letter ‘v’) for disjunction or class union. From his Calcolo geometrico onward, he instead used ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ for both (and ‘
$\mathrel {\boldsymbol {\cup }}$
’ for both (and ‘
![]() $\mathrel {\boldsymbol {\cap }}$
’ for conjunction and class intersection).
$\mathrel {\boldsymbol {\cap }}$
’ for conjunction and class intersection).
2. By the expression
![]() $A \mathrel {\boldsymbol {\cap }} B \mathrel {\boldsymbol {\cap }} C\mathrel {\boldsymbol {\cap }} \dots $
, or
$A \mathrel {\boldsymbol {\cap }} B \mathrel {\boldsymbol {\cap }} C\mathrel {\boldsymbol {\cap }} \dots $
, or
![]() $ABC\dots $
, we mean the largest class contained in the classes A, B, C, … or the class formed by all the entities which are at the same time in A and B and C, etc. The sign
$ABC\dots $
, we mean the largest class contained in the classes A, B, C, … or the class formed by all the entities which are at the same time in A and B and C, etc. The sign
![]() $\mathrel {\boldsymbol {\cap }}$
is read and; the operation is indicated by the sign
$\mathrel {\boldsymbol {\cap }}$
is read and; the operation is indicated by the sign
![]() $\mathrel {\boldsymbol {\cap }}$
is logical conjunction. We shall also call it logical multiplication, and say that the classes
$\mathrel {\boldsymbol {\cap }}$
is logical conjunction. We shall also call it logical multiplication, and say that the classes
![]() $A, B, \dots $
are factors of the product
$A, B, \dots $
are factors of the product
![]() $AB\dots $
$AB\dots $
3. By the expression
![]() $A \mathrel {\boldsymbol {\cup }} B \mathrel {\boldsymbol {\cup }} C \dots $
, we mean the smallest class which contains the classes A, B, C, … or the class formed by all the entities which are in A or B or C, etc. The sign
$A \mathrel {\boldsymbol {\cup }} B \mathrel {\boldsymbol {\cup }} C \dots $
, we mean the smallest class which contains the classes A, B, C, … or the class formed by all the entities which are in A or B or C, etc. The sign
![]() $\mathrel {\boldsymbol {\cup }}$
is read or; the operation is indicated by the sign
$\mathrel {\boldsymbol {\cup }}$
is read or; the operation is indicated by the sign
![]() $\mathrel {\boldsymbol {\cup }}$
is logical disjunction. We shall also call it logical addition, and say that the classes A, B, … are terms of the sum
$\mathrel {\boldsymbol {\cup }}$
is logical disjunction. We shall also call it logical addition, and say that the classes A, B, … are terms of the sum
![]() $A \mathrel {\boldsymbol {\cup }} B \mathrel {\boldsymbol {\cup }} \dots $
(Peano, Reference Peano1888, pp. 1–2; Reference Peano1973, p. 76)
$A \mathrel {\boldsymbol {\cup }} B \mathrel {\boldsymbol {\cup }} \dots $
(Peano, Reference Peano1888, pp. 1–2; Reference Peano1973, p. 76)
Similarly, Peano uses ‘
![]() $-A$
’ and ‘
$-A$
’ and ‘
![]() $\overline {A}$
’ for set complementation and interprets it also as negation; he uses ‘
$\overline {A}$
’ for set complementation and interprets it also as negation; he uses ‘
![]() $\bigcirc $
’ for the empty class and interprets
$\bigcirc $
’ for the empty class and interprets
![]() $A=\bigcirc $
as “there is no A”; and he uses ‘
$A=\bigcirc $
as “there is no A”; and he uses ‘
![]() ’ for the universal class and interprets
’ for the universal class and interprets
![]() as “everything is an A or a B” (Peano, Reference Peano1888, pp. 76–77).
as “everything is an A or a B” (Peano, Reference Peano1888, pp. 76–77).
Peano was of course aware of the then-entrenched use of ‘
![]() $+$
’ and ‘
$+$
’ and ‘
![]() $\cdot $
’ or ‘
$\cdot $
’ or ‘
![]() $\times $
’ for both disjunction and conjunction and for union and intersection in the algebra of logic tradition. He deliberately avoided using the same symbols in his own work, however:
$\times $
’ for both disjunction and conjunction and for union and intersection in the algebra of logic tradition. He deliberately avoided using the same symbols in his own work, however:
It seemed useful to substitute the symbols
![]() $\mathrel {\boldsymbol {\cap }}$
,
$\mathrel {\boldsymbol {\cap }}$
,
![]() $\mathrel {\boldsymbol {\cup }}$
,
$\mathrel {\boldsymbol {\cup }}$
,
![]() $- A$
,
$- A$
,
![]() $\bigcirc $
,
$\bigcirc $
,
![]() for the logical symbols
for the logical symbols
![]() $\times $
,
$\times $
,
![]() $+$
,
$+$
,
![]() $A_{\mathrm {i}}$
,
$A_{\mathrm {i}}$
,
![]() $0$
,
$0$
,
![]() $1$
used by Schröder, in order to forestall any possible confusion between the symbols of logic and those of mathematics (a thing otherwise advised by Schröder himself).Footnote
19
$1$
used by Schröder, in order to forestall any possible confusion between the symbols of logic and those of mathematics (a thing otherwise advised by Schröder himself).Footnote
19
The symbols ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ and ‘
$\mathrel {\boldsymbol {\cup }}$
’ and ‘
![]() $\mathrel {\boldsymbol {\cap }}$
’ are most likely adopted as typographical variants of ‘
$\mathrel {\boldsymbol {\cap }}$
’ are most likely adopted as typographical variants of ‘
![]() $\mathrel {\boldsymbol {\smallsmile }}$
’ and ‘
$\mathrel {\boldsymbol {\smallsmile }}$
’ and ‘
![]() $\mathrel {\boldsymbol {\smallfrown }}$
’ introduced by Grassmann (Reference Grassmann1844). Grassmann had used ‘
$\mathrel {\boldsymbol {\smallfrown }}$
’ introduced by Grassmann (Reference Grassmann1844). Grassmann had used ‘
![]() $\mathrel {\boldsymbol {\smallfrown }}$
’ as both a sign for an arbitrary operation (Verknüpfung) and as the sign for a kind of geometrical product. Leibniz had also sometimes used ‘
$\mathrel {\boldsymbol {\smallfrown }}$
’ as both a sign for an arbitrary operation (Verknüpfung) and as the sign for a kind of geometrical product. Leibniz had also sometimes used ‘
![]() $\mathrel {\boldsymbol {\smallfrown }}$
’ as a symbol for multiplication (e.g., Leibniz, Reference Leibniz1690, p. 5; reprinted in Leibniz, Reference Leibniz1858, p. 15), which Peano cites in Calcolo). Although Peano does not say, at least not in Calcolo, these uses may have suggested to him that ‘
$\mathrel {\boldsymbol {\smallfrown }}$
’ as a symbol for multiplication (e.g., Leibniz, Reference Leibniz1690, p. 5; reprinted in Leibniz, Reference Leibniz1858, p. 15), which Peano cites in Calcolo). Although Peano does not say, at least not in Calcolo, these uses may have suggested to him that ‘
![]() $\mathrel {\boldsymbol {\cap }}$
’ (or ‘
$\mathrel {\boldsymbol {\cap }}$
’ (or ‘
![]() $\mathrel {\boldsymbol {\smallfrown }}$
’) would be suitable to express logical multiplication (conjunction). He mentions Leibniz’s use of ‘
$\mathrel {\boldsymbol {\smallfrown }}$
’) would be suitable to express logical multiplication (conjunction). He mentions Leibniz’s use of ‘
![]() $\mathrel {\boldsymbol {\smallfrown }}$
’ for multiplication a decade later in the Formulaire:
$\mathrel {\boldsymbol {\smallfrown }}$
’ for multiplication a decade later in the Formulaire:
The sign
![]() $\mathrel {\boldsymbol {\smallfrown }}$
was adopted by Leibniz to indicate the arithmetical product. We adopt it for the logical product, since the arithmetical product is today indicated by
$\mathrel {\boldsymbol {\smallfrown }}$
was adopted by Leibniz to indicate the arithmetical product. We adopt it for the logical product, since the arithmetical product is today indicated by
![]() $\times $
.Footnote
20
$\times $
.Footnote
20
The propositional (re)interpretation of set-theoretic operators is purposeful: he extends (really, reaffirms) his propositional interpretation of the set-theoretic symbols in his treatment of propositions in Sections 1.4–1.11 on deductive logic, as was common practice among (other than Frege) logicians in the 1800s. Still, Peano explicitly uses ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ for propositional disjunction, e.g.:
$\mathrel {\boldsymbol {\cup }}$
’ for propositional disjunction, e.g.:
![]() $\alpha \mathrel {\boldsymbol {\cup }} \beta $
expresses the condition that
$\alpha \mathrel {\boldsymbol {\cup }} \beta $
expresses the condition that
![]() $\alpha $
is true or
$\alpha $
is true or
![]() $\beta $
is true. (Peano, Reference Peano1888, p. 82)
$\beta $
is true. (Peano, Reference Peano1888, p. 82)
Peano’s lower-case Greek letters may be (re)interpreted such that
![]() $\alpha \mathrel {\boldsymbol {\cup }} \beta $
is a union of classes wherever convenient. This sort of dual usage of symbols for classes or propositions, and for class operations or propositional connectives, allowed him to double-count proofs for analogous theorems.
$\alpha \mathrel {\boldsymbol {\cup }} \beta $
is a union of classes wherever convenient. This sort of dual usage of symbols for classes or propositions, and for class operations or propositional connectives, allowed him to double-count proofs for analogous theorems.
Peano persists in this dual usage in The Principles of Arithmetic (Peano, Reference Peano1889), where he used ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ as disjunction and class union, and ‘
$\mathrel {\boldsymbol {\cup }}$
’ as disjunction and class union, and ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ for both subset and implication (Peano, Reference Peano1889, pp. 105 and 108). Such dual usage drew a lengthy impeachment from Frege (Reference Frege1896, pp. 242–247). But in fairness to Peano, it leveraged Boole-style algebraic treatments in multiple domains at once, and Peano had philosophical reasons to so-use symbols.Footnote
21
By his principle of permanence, since the formal laws for propositional and class operators were identical (in his view), Peano rightly used the same notation for these different operators. This does not violate the first design principle of symbolism prohibiting ambiguous symbols: any symbol in a theorem or its proof must be unambiguous and the syntax is unimpeachable on this score. The intended interpretation, on the other hand, may vary in those limited cases such that the formal laws—even the theorems and their proofs—do not differ. Indeed, Peano was generally very thoughtful in his selection and use of symbols (see Schlimm, Reference Schlimm2021, for an insightful discussion). The “design principles” Peano employed explain, for instance, why he chose pairs of inverted symbols for dual operations like ‘
$\mathbin {\boldsymbol {\supset }}$
’ for both subset and implication (Peano, Reference Peano1889, pp. 105 and 108). Such dual usage drew a lengthy impeachment from Frege (Reference Frege1896, pp. 242–247). But in fairness to Peano, it leveraged Boole-style algebraic treatments in multiple domains at once, and Peano had philosophical reasons to so-use symbols.Footnote
21
By his principle of permanence, since the formal laws for propositional and class operators were identical (in his view), Peano rightly used the same notation for these different operators. This does not violate the first design principle of symbolism prohibiting ambiguous symbols: any symbol in a theorem or its proof must be unambiguous and the syntax is unimpeachable on this score. The intended interpretation, on the other hand, may vary in those limited cases such that the formal laws—even the theorems and their proofs—do not differ. Indeed, Peano was generally very thoughtful in his selection and use of symbols (see Schlimm, Reference Schlimm2021, for an insightful discussion). The “design principles” Peano employed explain, for instance, why he chose pairs of inverted symbols for dual operations like ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ and ‘
$\mathrel {\boldsymbol {\cup }}$
’ and ‘
![]() $\mathrel {\boldsymbol {\cap }}$
’.Footnote
22
$\mathrel {\boldsymbol {\cap }}$
’.Footnote
22
Peano’s habit of using one symbol for different notions—that is, for allowing the intended interpretation to vary in order to economize the amount of thought required to master the new symbols—is important to note because it helps explain the genealogy of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’. Russell will at first copy Peano’s practice, although Russell was more uncomfortable than Peano with using the same symbol under two distinct intended interpretations. Even where the formal laws were identical, as in the case of class notions and their relational analogues, Principia avoids using the exact same symbol for two different notions. Rather, the distinction is marked in the syntax of the system by using a different symbol entirely for different kinds of terms, as we will see in the next section. Still, Russell did use similar symbols for notions whose formal laws were close analogues, distinguishing these different symbols often by a small change, like a dot or an accent, in a Peano-like fashion. Thus Russell first used ‘
$\mathbin {\boldsymbol {\vee }}$
’. Russell will at first copy Peano’s practice, although Russell was more uncomfortable than Peano with using the same symbol under two distinct intended interpretations. Even where the formal laws were identical, as in the case of class notions and their relational analogues, Principia avoids using the exact same symbol for two different notions. Rather, the distinction is marked in the syntax of the system by using a different symbol entirely for different kinds of terms, as we will see in the next section. Still, Russell did use similar symbols for notions whose formal laws were close analogues, distinguishing these different symbols often by a small change, like a dot or an accent, in a Peano-like fashion. Thus Russell first used ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for a set-theoretic notion (relational product) and for propositional disjunction, and then later uses it just for propositional disjunction.Footnote
23
What Russell never does is to use the exact same symbol for distinct intended interpretations: these are always marked in the formal grammar by a different, even if highly similar, symbol.
$\mathbin {\boldsymbol {\vee }}$
’ for a set-theoretic notion (relational product) and for propositional disjunction, and then later uses it just for propositional disjunction.Footnote
23
What Russell never does is to use the exact same symbol for distinct intended interpretations: these are always marked in the formal grammar by a different, even if highly similar, symbol.
This is not to impeach Peano’s practice. Peano may have felt justified in his ambiguous use of ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ and ‘
$\mathrel {\boldsymbol {\cup }}$
’ and ‘
![]() $\mathrel {\boldsymbol {\cap }}$
’ by the principle of permanence, according to which operations obeying the same laws in different domains should be symbolized by the same notation (e.g., ‘
$\mathrel {\boldsymbol {\cap }}$
’ by the principle of permanence, according to which operations obeying the same laws in different domains should be symbolized by the same notation (e.g., ‘
![]() $+$
’ and ‘
$+$
’ and ‘
![]() $\cdot $
’ applied to different sets of numbers, say, integers and reals), and if not, they should be symbolized differently. Since the laws governing class union and intersection, and the laws for propositional disjunction and conjunction are the same, this justifies the use of the same symbols for both. By contrast, the arithmetical operations
$\cdot $
’ applied to different sets of numbers, say, integers and reals), and if not, they should be symbolized differently. Since the laws governing class union and intersection, and the laws for propositional disjunction and conjunction are the same, this justifies the use of the same symbols for both. By contrast, the arithmetical operations
![]() $+$
and
$+$
and
![]() $\cdot $
obey different laws, e.g., idempotence fails (see Toader, Reference Toader2021, for discussion). Moreover, context disambiguates between the different meanings of ‘
$\cdot $
obey different laws, e.g., idempotence fails (see Toader, Reference Toader2021, for discussion). Moreover, context disambiguates between the different meanings of ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ and ‘
$\mathrel {\boldsymbol {\cup }}$
’ and ‘
![]() $\mathrel {\boldsymbol {\cap }}$
’. By contrast, Peano’s class-theoretic construction of numbers in Arithmetices principia and later the Formulaire has him using both ‘
$\mathrel {\boldsymbol {\cap }}$
’. By contrast, Peano’s class-theoretic construction of numbers in Arithmetices principia and later the Formulaire has him using both ‘
![]() $+$
’ and ‘
$+$
’ and ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ between class terms, and so using the same symbol here would lead to ineliminable ambiguity.Footnote
24
$\mathrel {\boldsymbol {\cup }}$
’ between class terms, and so using the same symbol here would lead to ineliminable ambiguity.Footnote
24
We have already mentioned that Peano adapted his symbol ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ from Grassmann’s ‘
$\mathrel {\boldsymbol {\cup }}$
’ from Grassmann’s ‘
![]() $\mathrel {\boldsymbol {\smallsmile }}$
’. Is there any evidence that Peano was influenced in his choice also by the similarity to the initial v of vel, or specifically by Leibniz’s use of ‘
$\mathrel {\boldsymbol {\smallsmile }}$
’. Is there any evidence that Peano was influenced in his choice also by the similarity to the initial v of vel, or specifically by Leibniz’s use of ‘
![]() ’ for “or”? Peano was already aware of Leibniz’s use of ‘
’ for “or”? Peano was already aware of Leibniz’s use of ‘
![]() ’ as a symbol for disjunction when he introduced his own: he cites the very page of Mathematische Schriften where it occurs in Calcolo (Peano, Reference Peano1888, p. x). In his subsequent writings on logic, he often mentions the fact that Leibniz had used ‘v’ this way (though Peano omits the accent), and specifically that he did it because ‘v’ is the initial letter of vel:Footnote
25
’ as a symbol for disjunction when he introduced his own: he cites the very page of Mathematische Schriften where it occurs in Calcolo (Peano, Reference Peano1888, p. x). In his subsequent writings on logic, he often mentions the fact that Leibniz had used ‘v’ this way (though Peano omits the accent), and specifically that he did it because ‘v’ is the initial letter of vel:Footnote
25
Instead of
![]() $a\mathrel {\boldsymbol {\cup }} b$
Leibniz has
$a\mathrel {\boldsymbol {\cup }} b$
Leibniz has
![]() $a \mathbin {\mathrm {u}} b$
(where u is the initial of uel)…Footnote
26
$a \mathbin {\mathrm {u}} b$
(where u is the initial of uel)…Footnote
26
The sign
![]() $\circ $
corresponds to Latin aut; the sign
$\circ $
corresponds to Latin aut; the sign
![]() $\mathrel {\boldsymbol {\cup }}$
to vel.Footnote
27
$\mathrel {\boldsymbol {\cup }}$
to vel.Footnote
27
Leibniz, in his Schriften, vol. VII p. 57, indicates logical addition by ‘
![]() $a \mathbin {\mathrm {u}} b$
’; the letter u is the initial of the word uel.Footnote
28
$a \mathbin {\mathrm {u}} b$
’; the letter u is the initial of the word uel.Footnote
28
However, Peano avoided a symbol reminiscent of ‘v’ for disjunction to avoid confusion with other symbols: indeed, Peano already used ‘v’ for the universal class (Peano, Reference Peano1895, p. 139, Reference Peano1897, p. 13). Peano merely suggests that ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ for disjunction can be thought of as a deformation of the ‘v’ in vel:Footnote
29
$\mathrel {\boldsymbol {\cup }}$
’ for disjunction can be thought of as a deformation of the ‘v’ in vel:Footnote
29
![]() Let p and q be P [propositions];
Let p and q be P [propositions];
![]() $p \mathrel {\boldsymbol {\cup }} q$
means “at least one of these P is true”
$p \mathrel {\boldsymbol {\cup }} q$
means “at least one of these P is true”
One may read the sign “
![]() $\mathrel {\boldsymbol {\cup }}$
” as “or”; this operation is called logical addition.…
$\mathrel {\boldsymbol {\cup }}$
” as “or”; this operation is called logical addition.…
Leibniz has indicated the operation
![]() $\mathrel {\boldsymbol {\cup }}$
by the sign
$\mathrel {\boldsymbol {\cup }}$
by the sign
![]() $+$
(Leibniz, Reference Leibniz1890, p. 229); later (p. 237) by the same sign inside a circle. We cannot use a common sign for arithmetical and logical additions without producing ambiguities …
$+$
(Leibniz, Reference Leibniz1890, p. 229); later (p. 237) by the same sign inside a circle. We cannot use a common sign for arithmetical and logical additions without producing ambiguities …
One may consider the sign
![]() $\mathrel {\boldsymbol {\cup }}$
as a deformation of v, the initial letter of “vel,” used by Leibniz as well for the same purpose. However, in the “Arithmetices principia” (Peano, Reference Peano1889), which contains the first theory rendered in symbols, I have chosen the shape of logical signs in such a way as to avoid any confusion.Footnote
30
$\mathrel {\boldsymbol {\cup }}$
as a deformation of v, the initial letter of “vel,” used by Leibniz as well for the same purpose. However, in the “Arithmetices principia” (Peano, Reference Peano1889), which contains the first theory rendered in symbols, I have chosen the shape of logical signs in such a way as to avoid any confusion.Footnote
30
So even though Peano often suggested a connection between the symbol for disjunction and the Latin vel, it is unlikely that his choice of ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ for “or” was originally motivated by this connection. Russell likely got the idea of using ‘
$\mathrel {\boldsymbol {\cup }}$
’ for “or” was originally motivated by this connection. Russell likely got the idea of using ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction from Peano, whom he read closely.Footnote
31
This is not terribly surprising: indeed, it is hard to overstate Peano’s influence on Principia’s notations. Even Whitehead (Reference Whitehead1898) followed Boole and symbolized disjunction and conjunction as addition and multiplication before encountering Peano’s work. After becoming thoroughly familiar with Peano’s work through Russell, Whitehead (Reference Whitehead1902) also adopted Peano’s ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction from Peano, whom he read closely.Footnote
31
This is not terribly surprising: indeed, it is hard to overstate Peano’s influence on Principia’s notations. Even Whitehead (Reference Whitehead1898) followed Boole and symbolized disjunction and conjunction as addition and multiplication before encountering Peano’s work. After becoming thoroughly familiar with Peano’s work through Russell, Whitehead (Reference Whitehead1902) also adopted Peano’s ‘
![]() $\mathrel {\boldsymbol {\cap }}$
’ and ‘
$\mathrel {\boldsymbol {\cap }}$
’ and ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’. Whitehead & Russell (Reference Whitehead and Russell1910, p. vii) fully acknowledge Peano’s notational impact: “In the matter of notation, we have as far as possible followed Peano…”
$\mathrel {\boldsymbol {\cup }}$
’. Whitehead & Russell (Reference Whitehead and Russell1910, p. vii) fully acknowledge Peano’s notational impact: “In the matter of notation, we have as far as possible followed Peano…”
Yet in using ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction, Principia departs from Peano’s notations. As we will see in the next section, Whitehead and Russell are jointly responsible for this. The earliest surviving use of ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction, Principia departs from Peano’s notations. As we will see in the next section, Whitehead and Russell are jointly responsible for this. The earliest surviving use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction we could find is in a Whitehead manuscript, but Russell may well be the one who introduced the symbol. He first separated the notations for class union and propositional disjunction. Russell also used ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction we could find is in a Whitehead manuscript, but Russell may well be the one who introduced the symbol. He first separated the notations for class union and propositional disjunction. Russell also used ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction in solo published work some years before the co-authored Principia was published. The next section supplies the evidence for this summary.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction in solo published work some years before the co-authored Principia was published. The next section supplies the evidence for this summary.
5 Whitehead and Russell
We give Whitehead and Russell joint credit for first using ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction. The relevant surviving manuscripts from Whitehead and Russell were written in close proximity, but the relative dating is uncertain. Moreover, many manuscripts from the time of the writing of Principia are lost. In any case, one of Whitehead and Russell, or both jointly, first used ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction. The relevant surviving manuscripts from Whitehead and Russell were written in close proximity, but the relative dating is uncertain. Moreover, many manuscripts from the time of the writing of Principia are lost. In any case, one of Whitehead and Russell, or both jointly, first used ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction. Their use of this notation, through the influence of Principia, is the reason for today’s wide acceptance of it (as we argue in the next section).
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction. Their use of this notation, through the influence of Principia, is the reason for today’s wide acceptance of it (as we argue in the next section).
After framing the timeline for our discussion, we trace the genealogy of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ in the surviving manuscripts. We will start from what is definitely known and conclude this section with what is merely probable. In our genealogy of Whitehead and Russell’s design principles for notation we also focus on Russell’s publications and manuscripts because few of Whitehead’s pre-Principia manuscripts from this period survive.Footnote
32
Our aim is to correctly trace the evolution of Principia’s notations, and the design principles for choosing them. Crediting either Russell or Whitehead with any specific decision is difficult for the above reasons. Thus, even where we consider a single-authored manuscript or publication and write of, e.g., as Russell introducing a symbol, we do not mean to imply that Russell alone deserves the credit. We have no doubt that Whitehead and Russell agreed on the design principles for notations as they are manifested in Principia.
$\mathbin {\boldsymbol {\vee }}$
’ in the surviving manuscripts. We will start from what is definitely known and conclude this section with what is merely probable. In our genealogy of Whitehead and Russell’s design principles for notation we also focus on Russell’s publications and manuscripts because few of Whitehead’s pre-Principia manuscripts from this period survive.Footnote
32
Our aim is to correctly trace the evolution of Principia’s notations, and the design principles for choosing them. Crediting either Russell or Whitehead with any specific decision is difficult for the above reasons. Thus, even where we consider a single-authored manuscript or publication and write of, e.g., as Russell introducing a symbol, we do not mean to imply that Russell alone deserves the credit. We have no doubt that Whitehead and Russell agreed on the design principles for notations as they are manifested in Principia.
Here is the time frame for the remainder of this section: in his 1901 “The Logic of Relations” (Reference Russell1901), Russell took implication as a primitive symbol. In Whitehead and Russell’s 1910 Principia, ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction is now primitive (Whitehead & Russell, Reference Whitehead and Russell1910, p. 93). This raises two questions about Russell’s development: (1) When and why was disjunction taken as primitive? and (2) When and why was ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction is now primitive (Whitehead & Russell, Reference Whitehead and Russell1910, p. 93). This raises two questions about Russell’s development: (1) When and why was disjunction taken as primitive? and (2) When and why was ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ introduced for disjunction?
$\mathbin {\boldsymbol {\vee }}$
’ introduced for disjunction?
We first take up (1). To answer the “why” part: disjunction is taken as primitive because the resulting system is simpler in that it has fewer primitive propositions.Footnote
33
In Principia, Whitehead & Russell (Reference Whitehead and Russell1910, p. 130) comment on
![]() , which is
, which is
![]() :
:
From
![]() it appears that we might have taken implication, instead of disjunction, as a primitive idea, and have defined “
it appears that we might have taken implication, instead of disjunction, as a primitive idea, and have defined “
![]() $p \mathbin {\boldsymbol {\vee }} q$
” as meaning “
$p \mathbin {\boldsymbol {\vee }} q$
” as meaning “
![]() .” This course, however, requires more primitive propositions than are required by the method we have adopted.
.” This course, however, requires more primitive propositions than are required by the method we have adopted.
If we set aside inference rules and consider just propositional axioms or axiom schemata, the texts bear out this claim. “The Theory of Implication” (Russell, Reference Russell1906) gives seven axioms for propositional logic; Principia instead has five.Footnote 34
The “when” part of question (1) can be answered using the Couturat–Russell letters translated in the headnote to Russell (Reference Russell1906). The first known evidence of the switch from ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ being primitive to ‘
$\mathbin {\boldsymbol {\supset }}$
’ being primitive to ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ being primitive is from August 21, 1906.
$\mathbin {\boldsymbol {\vee }}$
’ being primitive is from August 21, 1906.
Russell wrote “The Theory of Implication” in the summer of 1905, and it was published in the American Journal of Mathematics in April 1906. Again, Russell adopts (material) implication as a primitive therein. Russell justifies ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ being primitive explicitly on much the same grounds as he later justifies replacing ‘
$\mathbin {\boldsymbol {\supset }}$
’ being primitive explicitly on much the same grounds as he later justifies replacing ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ with ‘
$\mathbin {\boldsymbol {\supset }}$
’ with ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ as primitive: “it avoids hypotheses which are otherwise necessary” (Russell, Reference Russell1906, p. 162). What hypotheses does Russell avoid in the 1906 paper? As a footnote makes clear (Russell, Reference Russell1906, p. 162), these hypotheses are to the effect that for any p and q, if
$\mathbin {\boldsymbol {\vee }}$
’ as primitive: “it avoids hypotheses which are otherwise necessary” (Russell, Reference Russell1906, p. 162). What hypotheses does Russell avoid in the 1906 paper? As a footnote makes clear (Russell, Reference Russell1906, p. 162), these hypotheses are to the effect that for any p and q, if
![]() $p \mathbin {\boldsymbol {\supset }} q$
, then p and q are propositions, and so are truth-apt. These hypotheses are adopted in The Principles of Mathematics (Russell, Reference Russell1903c) to prevent the relation of material implication from obtaining between any non-propositional (truth-inapt) entities.
$p \mathbin {\boldsymbol {\supset }} q$
, then p and q are propositions, and so are truth-apt. These hypotheses are adopted in The Principles of Mathematics (Russell, Reference Russell1903c) to prevent the relation of material implication from obtaining between any non-propositional (truth-inapt) entities.
Recall that Russell’s “calculus of propositions,” also known as the substitutional theory, allowed for variables to range over everything without restriction (Linsky, Reference Linsky and Costreie2016, p. 224). Landini (Reference Landini1996, p. 558) calls this “the doctrine of the unrestricted variable” because on this theory variables range over all entities whatever (rather than, say, different sorts of variables ranging over objects and predicates, as is now common in presentations of second-order logic). This was only possible because the notions of ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ in Russell (Reference Russell1903c, Reference Russell1906) were quite different from the modern one and that of the 1910 Principia. On the earlier substitutional theory, the sign ‘
$\mathbin {\boldsymbol {\supset }}$
’ in Russell (Reference Russell1903c, Reference Russell1906) were quite different from the modern one and that of the 1910 Principia. On the earlier substitutional theory, the sign ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ is a relation sign: it connects terms to make a term, so that “Socrates
$\mathbin {\boldsymbol {\supset }}$
’ is a relation sign: it connects terms to make a term, so that “Socrates
![]() $\mathbin {\boldsymbol {\supset }}$
Socrates” was well-formed in Russell’s early systems. The modern sign for implication ‘
$\mathbin {\boldsymbol {\supset }}$
Socrates” was well-formed in Russell’s early systems. The modern sign for implication ‘
![]() $\rightarrow $
’, like the symbol ‘
$\rightarrow $
’, like the symbol ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ in Principia, behaves very differently: it connects well-formed formulas to make a well-formed formula, so that “Socrates
$\mathbin {\boldsymbol {\supset }}$
’ in Principia, behaves very differently: it connects well-formed formulas to make a well-formed formula, so that “Socrates
![]() $\rightarrow $
Socrates” is syntactically ill-formed (much like “a
$\rightarrow $
Socrates” is syntactically ill-formed (much like “a
![]() $\rightarrow $
a” is ungrammatical in most modern systems).
$\rightarrow $
a” is ungrammatical in most modern systems).
Of course, the primitive postulates in Russell (Reference Russell1903c, sec. 18) precluded any material implication relations obtaining between non-propositional entities even though such strings could be syntactically well-formed: one does not want to allow that “Socrates implies Socrates” is a truth of one’s formal system (and this is not a theorem in either early system). How did Russell prevent, say, “Socrates
![]() $\mathbin {\boldsymbol {\supset }}$
Socrates” from being even vacuously true in the 1903 system while preserving the doctrine of the unrestricted variable under which any term is substitutable for a variable? Russell built into some primitive propositions of the 1903 system the antecedent condition that p is a proposition. For example, in place of the axiom
$\mathbin {\boldsymbol {\supset }}$
Socrates” from being even vacuously true in the 1903 system while preserving the doctrine of the unrestricted variable under which any term is substitutable for a variable? Russell built into some primitive propositions of the 1903 system the antecedent condition that p is a proposition. For example, in place of the axiom
![]() $p \mathbin {\boldsymbol {\supset }} p$
, Russell had
$p \mathbin {\boldsymbol {\supset }} p$
, Russell had
![]() , which on Russell’s intended interpretation is tantamount to adding the condition “whatever implies anything is a proposition” (Russell, Reference Russell1903c, sec. 18).
, which on Russell’s intended interpretation is tantamount to adding the condition “whatever implies anything is a proposition” (Russell, Reference Russell1903c, sec. 18).
In “Theory of Implication,” (Russell, Reference Russell1906,
![]() ) instead interprets ‘
) instead interprets ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ in such a way that it may be just vacuously false whenever truth-inapt terms flank it, making the further hypothesis that whatever implies anything is a proposition redundant.Footnote
35
Russell’s intended interpretation of the 1906 system effects some simplification of the primitive propositions in the 1906 system as compared with the 1903 one.Footnote
36
$\mathbin {\boldsymbol {\supset }}$
’ in such a way that it may be just vacuously false whenever truth-inapt terms flank it, making the further hypothesis that whatever implies anything is a proposition redundant.Footnote
35
Russell’s intended interpretation of the 1906 system effects some simplification of the primitive propositions in the 1906 system as compared with the 1903 one.Footnote
36
At any rate, in 1906 Russell still takes ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ as primitive. Russell finally introduces ‘
$\mathbin {\boldsymbol {\supset }}$
’ as primitive. Russell finally introduces ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction in
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction in
![]() (Russell, Reference Russell1906, p. 176), which defines
(Russell, Reference Russell1906, p. 176), which defines
![]() $p \mathbin {\boldsymbol {\vee }} q$
as
$p \mathbin {\boldsymbol {\vee }} q$
as
![]() $\mathord {\boldsymbol {\sim }} p \mathbin {\boldsymbol {\supset }} q$
. The first passage of the section makes clear that ‘
$\mathord {\boldsymbol {\sim }} p \mathbin {\boldsymbol {\supset }} q$
. The first passage of the section makes clear that ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ means disjunction (“propositional sum”):
$\mathbin {\boldsymbol {\vee }}$
’ means disjunction (“propositional sum”):
In this section we shall be concerned with the fundamental properties of the propositional product and the propositional sum of two entities p and q… The propositional sum of p and q is practically “either p is true or q is true.” We avoid a new primitive idea by taking as the propositional sum
![]() $\mathord {\boldsymbol {\sim }} p \mathbin {\boldsymbol {\supset }} q$
, i.e., “if p is not true, then q is true.” There are some advantages in taking the propositional sum as a primitive idea instead of ‘
$\mathord {\boldsymbol {\sim }} p \mathbin {\boldsymbol {\supset }} q$
, i.e., “if p is not true, then q is true.” There are some advantages in taking the propositional sum as a primitive idea instead of ‘
![]() $p \mathbin {\boldsymbol {\supset }} q$
’; we then define ‘
$p \mathbin {\boldsymbol {\supset }} q$
’; we then define ‘
![]() $p \mathbin {\boldsymbol {\supset }} q$
’ as the propositional sum of
$p \mathbin {\boldsymbol {\supset }} q$
’ as the propositional sum of
![]() $\mathord {\boldsymbol {\sim }} p$
and q. The choice is a matter of taste. (Russell, Reference Russell1906, p. 175)
$\mathord {\boldsymbol {\sim }} p$
and q. The choice is a matter of taste. (Russell, Reference Russell1906, p. 175)
As this quotation shows, Russell was obviously not wedded to one or another choice of primitive in his 1906 paper and allows that either one can define the other. This is a significant shift from his view in Principles, where he explicitly argues that implication cannot be defined, even in terms of equivalent formulas using other connectives (Russell, Reference Russell1903c, sec. 16).
Shortly after publication of “Theory of implication,” Russell found a reason to prefer disjunction as a primitive notion over implication: it reduced the number of axioms needed for propositional logic. Couturat and Russell exchanged letters about Russell’s 1906 paper. On August 21, 1906, Russell wrote to Couturat to announce his discovery that taking ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ as primitive simplifies the development of his logic:
$\mathbin {\boldsymbol {\vee }}$
’ as primitive simplifies the development of his logic:
One can take as a primitive idea
![]() $p \mathbin {\boldsymbol {\vee }} q$
, while defining
$p \mathbin {\boldsymbol {\vee }} q$
, while defining
In this way two primitive propositions are made superfluous. (Russell, Reference Russell and Schmid2001, #216)
This answers question (1): by August 21, 1906, Russell took disjunction as primitive instead of material implication, and he did this because it was logically simpler, that is, it reduced the number of axioms needed in propositional logic.
Now for question (2): when and why did Whitehead and/or Russell first choose the symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction? Unlike Peano, Whitehead and Russell never explicitly explained this choice of notation. So we will have to reconstruct their reasons.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction? Unlike Peano, Whitehead and Russell never explicitly explained this choice of notation. So we will have to reconstruct their reasons.
The two natural conjectures are that (A) Whitehead and Russell adopted ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ because Leibniz used ‘
$\mathbin {\boldsymbol {\vee }}$
’ because Leibniz used ‘
![]() ’ and (B) Whitehead and Russell adopted ‘
’ and (B) Whitehead and Russell adopted ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ as a modification of the already available notation ‘
$\mathbin {\boldsymbol {\vee }}$
’ as a modification of the already available notation ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’. Given the available evidence, we endorse (B). First let us consider why (A) is improbable.
$\mathrel {\boldsymbol {\cup }}$
’. Given the available evidence, we endorse (B). First let us consider why (A) is improbable.
If one supposes that Whitehead and Russell got ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ from Leibniz, the next question to answer is, ‘How did Whitehead and Russell come across it?’ Here there are two natural possibilities: (A1) Whitehead and Russell found a use of ‘
$\mathbin {\boldsymbol {\vee }}$
’ from Leibniz, the next question to answer is, ‘How did Whitehead and Russell come across it?’ Here there are two natural possibilities: (A1) Whitehead and Russell found a use of ‘
![]() ’ in Leibniz independently, or (A2) Whitehead and Russell found out about this possibility through Peano, who, as we saw, did notice Leibniz’s use of ‘
’ in Leibniz independently, or (A2) Whitehead and Russell found out about this possibility through Peano, who, as we saw, did notice Leibniz’s use of ‘
![]() ’.
’.
Against (A1), there is no textual evidence, for instance, in Russell (Reference Russell1900a), that Whitehead or Russell encountered, on their own, Leibniz’s sole manuscript in which ‘
![]() ’ is used for disjunction. Indeed, there is no evidence that Whitehead or Russell ever owned Leibnizens mathematische Schriften. No notes on these volumes occur in Russell’s Leibniz notebooks (Arthur & Griffin, Reference Arthur and Griffin2017). Leibnizens mathematische Schriften are also not in Russell’s library, which is held at the Bertrand Russell Research Centre. By contrast, Russell’s library has all seven volumes of the Philosophischen Schriften, which he annotated heavily; these annotations were published by Arthur, Galaugher, & Griffin (Reference Arthur, Galaugher and Griffin2017). Furthermore, Russell kept a list of books he was reading from 1891 to 1902 (Russell, Reference Russell1891). None of Leibnizens mathematische Schriften appear on this list of books (O’Briant, Reference O’Briant1979, pp. 165–166). Finally, Russell’s citations of Leibnizens mathematische Schriften are sparse enough to have been pulled from other authors who quoted from them directly.Footnote
37
So it is probable that Russell never saw the manuscript in question, or even the volume in which it was available.Footnote
38
Similar reasoning applies to Whitehead, whose 1898 A Treatise on Universal Algebra cites Leibniz (as “Leibnitz”) just once, discussing a theorem about resultant forces. And Whitehead reports, “My knowledge of Leibniz’s investigations [when I wrote the Treatise] was entirely based on Couturat’s book, La Logique de Leibniz, published in 1901” (Whitehead, Reference Whitehead and Schilpp1941, p. 10). In summary, it is consistent with the available evidence that neither Whitehead nor Russell ever directly saw Leibniz’s use of ‘
’ is used for disjunction. Indeed, there is no evidence that Whitehead or Russell ever owned Leibnizens mathematische Schriften. No notes on these volumes occur in Russell’s Leibniz notebooks (Arthur & Griffin, Reference Arthur and Griffin2017). Leibnizens mathematische Schriften are also not in Russell’s library, which is held at the Bertrand Russell Research Centre. By contrast, Russell’s library has all seven volumes of the Philosophischen Schriften, which he annotated heavily; these annotations were published by Arthur, Galaugher, & Griffin (Reference Arthur, Galaugher and Griffin2017). Furthermore, Russell kept a list of books he was reading from 1891 to 1902 (Russell, Reference Russell1891). None of Leibnizens mathematische Schriften appear on this list of books (O’Briant, Reference O’Briant1979, pp. 165–166). Finally, Russell’s citations of Leibnizens mathematische Schriften are sparse enough to have been pulled from other authors who quoted from them directly.Footnote
37
So it is probable that Russell never saw the manuscript in question, or even the volume in which it was available.Footnote
38
Similar reasoning applies to Whitehead, whose 1898 A Treatise on Universal Algebra cites Leibniz (as “Leibnitz”) just once, discussing a theorem about resultant forces. And Whitehead reports, “My knowledge of Leibniz’s investigations [when I wrote the Treatise] was entirely based on Couturat’s book, La Logique de Leibniz, published in 1901” (Whitehead, Reference Whitehead and Schilpp1941, p. 10). In summary, it is consistent with the available evidence that neither Whitehead nor Russell ever directly saw Leibniz’s use of ‘
![]() ’.
’.
It is of course true that Whitehead and Russell had some first-hand acquaintance with Latin and Greek thanks to their pre-college education. Russell was educated in Latin and Greek, in addition to being fluent in French and German. Might it be possible that Russell wanted to associate propositional disjunction with ‘vel’ even if he never saw the occurrence in Leibniz? We find this quite unlikely because Russell despised Latin (and Greek), writing in his (Russell, Reference Russell1967, p. 36), “I hated Latin and Greek, and thought it merely foolish to learn a language that nobody speaks.” (Happily, he did not feel similarly about logical languages.) Moreover, as Lenz (Reference Lenz1987, p. 105) notes, “The learning of Latin and Greek played only a small role in [Russell’s] tutelage.” Even if Peano’s remarks about Leibniz may have caused Russell to think of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ when deciding on a symbol to represent disjunction, there is no reason to think that a connection to vel motivated Russell’s choice of ‘
$\mathbin {\boldsymbol {\vee }}$
’ when deciding on a symbol to represent disjunction, there is no reason to think that a connection to vel motivated Russell’s choice of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’, and some reason to think that Latin associations would have been, if anything, wholly repugnant to him. Whitehead also studied Latin and Greek early on, but there is little evidence to suggest this connection with vel would have occurred to Whitehead (or have felt apt to impress the new symbol’s meaning upon the mathematical community). Indeed, Whitehead’s education early on let Latin take a backseat to mathematics: “I was excused in the composition of Latin Verse and the reading of some Latin poetry, in order to give more time for mathematics” (Whitehead, Reference Whitehead and Schilpp1941, p. 6).
$\mathbin {\boldsymbol {\vee }}$
’, and some reason to think that Latin associations would have been, if anything, wholly repugnant to him. Whitehead also studied Latin and Greek early on, but there is little evidence to suggest this connection with vel would have occurred to Whitehead (or have felt apt to impress the new symbol’s meaning upon the mathematical community). Indeed, Whitehead’s education early on let Latin take a backseat to mathematics: “I was excused in the composition of Latin Verse and the reading of some Latin poetry, in order to give more time for mathematics” (Whitehead, Reference Whitehead and Schilpp1941, p. 6).
On the other hand, in support of (A2), Whitehead and Russell were close readers of Peano’s works, including the Formulaire, throughout the period from 1900 to 1903. In multiple works, Peano explicitly noted Leibniz’s use of ‘
![]() ’. So if one is to accept the view that ‘
’. So if one is to accept the view that ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ comes to us from Leibniz, Peano is the most probable intermediary source of Whitehead and Russell’s using ‘
$\mathbin {\boldsymbol {\vee }}$
’ comes to us from Leibniz, Peano is the most probable intermediary source of Whitehead and Russell’s using ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction, even if Peano never adopted Whitehead and Russell’s notation for disjunction. But against this proposal, there was a years-long delay between Whitehead and Russell’s close study of Peano’s works and their first uses of ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction, even if Peano never adopted Whitehead and Russell’s notation for disjunction. But against this proposal, there was a years-long delay between Whitehead and Russell’s close study of Peano’s works and their first uses of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’. Russell studied Peano’s works extensively in September 1900, just after the July 1900 Congress (Russell, Reference Russell1891, p. 363). Whitehead references the first three volumes of the Formulaire and praises the “admirable work” of Peano’s school in a footnote to his April 1901 “Memoir on the Algebra of Symbolic Logic” (Whitehead, Reference Whitehead1901, p. 140). However, as we will see, Russell first used ‘
$\mathbin {\boldsymbol {\vee }}$
’. Russell studied Peano’s works extensively in September 1900, just after the July 1900 Congress (Russell, Reference Russell1891, p. 363). Whitehead references the first three volumes of the Formulaire and praises the “admirable work” of Peano’s school in a footnote to his April 1901 “Memoir on the Algebra of Symbolic Logic” (Whitehead, Reference Whitehead1901, p. 140). However, as we will see, Russell first used ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ in his spring 1902 “On Likeness” manuscript, and Whitehead first uses it in his contemporaneous “The Logic of Propositional Functions” manuscript. So neither Whitehead nor Russell used this notation until many months after their deep study of Peano. This suggests it was not Leibniz’s notational choices that led Whitehead and Russell to adopt ‘
$\mathbin {\boldsymbol {\vee }}$
’ in his spring 1902 “On Likeness” manuscript, and Whitehead first uses it in his contemporaneous “The Logic of Propositional Functions” manuscript. So neither Whitehead nor Russell used this notation until many months after their deep study of Peano. This suggests it was not Leibniz’s notational choices that led Whitehead and Russell to adopt ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction, but some other development. We describe just such a development, consistent with hypothesis (B), that explains why Whitehead and Russell modified ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction, but some other development. We describe just such a development, consistent with hypothesis (B), that explains why Whitehead and Russell modified ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ to use ‘
$\mathrel {\boldsymbol {\cup }}$
’ to use ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction. Accordingly, we reject hypothesis (A).
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction. Accordingly, we reject hypothesis (A).
We saw above that Peano used ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ for both disjunction and class union—not ambiguously in a problematic sense, but so that one could follow a different intended interpretation of the symbol and retain all the formal laws governing ‘
$\mathrel {\boldsymbol {\cup }}$
’ for both disjunction and class union—not ambiguously in a problematic sense, but so that one could follow a different intended interpretation of the symbol and retain all the formal laws governing ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ and the proofs involving occurrences of ‘
$\mathrel {\boldsymbol {\cup }}$
’ and the proofs involving occurrences of ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’. This accords with the “design principle” for notations, the principle of permanence, discussed above. Russell seems to have accepted a similar principle, but not quite the same one. Indeed, even where the formal laws are identical, Principia distinguishes between different kinds of terms. So in Principia we find ‘
$\mathrel {\boldsymbol {\cup }}$
’. This accords with the “design principle” for notations, the principle of permanence, discussed above. Russell seems to have accepted a similar principle, but not quite the same one. Indeed, even where the formal laws are identical, Principia distinguishes between different kinds of terms. So in Principia we find ‘
![]() $\alpha \mathrel {\boldsymbol {\cup }} \beta $
’ for class union in
$\alpha \mathrel {\boldsymbol {\cup }} \beta $
’ for class union in
![]() $\mathord {\ast } 22$
and ‘
$\mathord {\ast } 22$
and ‘
![]() ’ for relational union (i.e., a union of ordered couples) in
’ for relational union (i.e., a union of ordered couples) in
![]() $\mathord {\ast } 23$
. This is despite the fact that “the definitions and propositions of this number [
$\mathord {\ast } 23$
. This is despite the fact that “the definitions and propositions of this number [
![]() $\mathord {\ast } 23$
] are to be exact analogues of those of
$\mathord {\ast } 23$
] are to be exact analogues of those of
![]() $\mathord {\ast } 22$
” (Whitehead & Russell, Reference Whitehead and Russell1910, p. 226).
$\mathord {\ast } 22$
” (Whitehead & Russell, Reference Whitehead and Russell1910, p. 226).
So Russell cannot have held that different notions should get the same notation even when the formal laws are identical. In rejecting Peano’s design principle here, Russell was likely further influenced by Frege’s sharp criticisms of Peano’s conceptual notations.Footnote
39
Indeed, as we will see below, the very manuscript wherein Russell first introduces ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction is written after Russell’s engagement with Frege’s writings (although Russell seems to have been moving in this direction already; see Urquhart, Reference Urquhart1994, p. xvii). Furthermore, Frege explicitly criticizes Peano’s alleged “twofold use” of symbols for propositional and class notions.Footnote
40
So if Russell introduced ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction is written after Russell’s engagement with Frege’s writings (although Russell seems to have been moving in this direction already; see Urquhart, Reference Urquhart1994, p. xvii). Furthermore, Frege explicitly criticizes Peano’s alleged “twofold use” of symbols for propositional and class notions.Footnote
40
So if Russell introduced ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ to distinguish propositional sum and class sum, as we think he did, the fact that Russell had just taken extensive notes on Frege’s writings (and Schröder’s writings—Schröder likewise criticized Peano for alleged dual uses of notation for propositional and class notions), it is no coincidence (Linsky, Reference Linsky2004).Footnote
41
All this supports conjecture (B): Russell introduced ‘
$\mathbin {\boldsymbol {\vee }}$
’ to distinguish propositional sum and class sum, as we think he did, the fact that Russell had just taken extensive notes on Frege’s writings (and Schröder’s writings—Schröder likewise criticized Peano for alleged dual uses of notation for propositional and class notions), it is no coincidence (Linsky, Reference Linsky2004).Footnote
41
All this supports conjecture (B): Russell introduced ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ to separate notations for two different notions—propositional sum and class sum—and was further influenced by Frege’s writings to do this.
$\mathbin {\boldsymbol {\vee }}$
’ to separate notations for two different notions—propositional sum and class sum—and was further influenced by Frege’s writings to do this.
Still, ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ did not appear ex nihilo. Rather, this symbol was a modification of the symbol ‘
$\mathbin {\boldsymbol {\vee }}$
’ did not appear ex nihilo. Rather, this symbol was a modification of the symbol ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’. Russell’s apparent practice, even after engaging with Frege’s work, was that similar notions should have similar notations. Admittedly, Russell never explicitly lays this down as a design principle for symbolism—he is far less explicit than Peano in this regard—but we know that Russell was, as he described himself, “fussy” about even minute aspects of how his writing appeared, such as where punctuation and paragraph breaks occurred, whether a colon or semicolon should be used, and formatting issues like italics (Blackwell, Reference Blackwell1983). Needless to say, Russell was a consciously conscientious designer of notations, even if he never made his design principles for notations explicit.
$\mathrel {\boldsymbol {\cup }}$
’. Russell’s apparent practice, even after engaging with Frege’s work, was that similar notions should have similar notations. Admittedly, Russell never explicitly lays this down as a design principle for symbolism—he is far less explicit than Peano in this regard—but we know that Russell was, as he described himself, “fussy” about even minute aspects of how his writing appeared, such as where punctuation and paragraph breaks occurred, whether a colon or semicolon should be used, and formatting issues like italics (Blackwell, Reference Blackwell1983). Needless to say, Russell was a consciously conscientious designer of notations, even if he never made his design principles for notations explicit.
That Russell embraced this design principle can be inferred from his notational design principles of (1) using similar symbols for similar notions (ones obeying analogous laws), and of (2) using distinct (even if similar) notations for distinct notions. There are many examples in Principia supporting that these two design principles were Russell’s apparent (if implicit) practice. For example, we find ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ and ‘
$\mathbin {\boldsymbol {\supset }}$
’ and ‘
![]() $\mathrel {\boldsymbol {\subset }}$
’ used in Principia for implication and class inclusion, respectively. We find ‘2’ and ‘
$\mathrel {\boldsymbol {\subset }}$
’ used in Principia for implication and class inclusion, respectively. We find ‘2’ and ‘
![]() $\dot {2}$
’ for the cardinal number 2 and the ordinal number 2, respectively. The formal laws governing these pairs of notions differ; nonetheless, Principia uses similar notations for them because they are analogous. Crucially, Principia never uses the same symbol for distinct notions whose formal laws differ.
$\dot {2}$
’ for the cardinal number 2 and the ordinal number 2, respectively. The formal laws governing these pairs of notions differ; nonetheless, Principia uses similar notations for them because they are analogous. Crucially, Principia never uses the same symbol for distinct notions whose formal laws differ.
This fact helps us answer the ‘why’ part of question (2): we maintain that Russell chose ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction because he was keen to separate symbols for propositional and class notions because he held that their formal laws differed. In this Russell was unlike Peano who deliberately wed them together, since he held that the formal laws that each obeyed were the same. Russell’s choice of ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction because he was keen to separate symbols for propositional and class notions because he held that their formal laws differed. In this Russell was unlike Peano who deliberately wed them together, since he held that the formal laws that each obeyed were the same. Russell’s choice of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ thus mimics Peano’s practice of using some symbols dually for propositional connectives and class operators: Russell wants to analogize the notions expressed by ‘
$\mathbin {\boldsymbol {\vee }}$
’ thus mimics Peano’s practice of using some symbols dually for propositional connectives and class operators: Russell wants to analogize the notions expressed by ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ and ‘
$\mathrel {\boldsymbol {\cup }}$
’ and ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’. But because the analogy was imperfect, in Russell’s view, Russell chose a new but similar symbol for propositional disjunction, namely, a sharpened, pointed ‘
$\mathbin {\boldsymbol {\vee }}$
’. But because the analogy was imperfect, in Russell’s view, Russell chose a new but similar symbol for propositional disjunction, namely, a sharpened, pointed ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’.
$\mathrel {\boldsymbol {\cup }}$
’.
Why did Russell think that ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ and ‘
$\mathbin {\boldsymbol {\vee }}$
’ and ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ obeyed distinct formal laws? In “The Theory of Implication” (Russell, Reference Russell1906, p. 190) he remarks:
$\mathrel {\boldsymbol {\cup }}$
’ obeyed distinct formal laws? In “The Theory of Implication” (Russell, Reference Russell1906, p. 190) he remarks:
The analogues, for classes, of
![]() , are false. Take, e.g.,
, are false. Take, e.g.,
![]() , and put
, and put
![]() $p = $
English people,
$p = $
English people,
![]() $q = $
men,
$q = $
men,
![]() $r = $
women. Then p is contained in q or r, but is not contained in q and is not contained in r.
$r = $
women. Then p is contained in q or r, but is not contained in q and is not contained in r.
This exact remark is repeated in Principia following
![]() . And Russell’s distinction of the propositional and class calculus goes back to Principles. In Section 25 of Principles (Russell, Reference Russell1903c), titled “Relation [of the calculus of classes] to propositional calculus,” Russell gives an example of a formula that “can only be truly interpreted in the propositional calculus: in the class-calculus it is false.” Russell then says this about disjunction:
. And Russell’s distinction of the propositional and class calculus goes back to Principles. In Section 25 of Principles (Russell, Reference Russell1903c), titled “Relation [of the calculus of classes] to propositional calculus,” Russell gives an example of a formula that “can only be truly interpreted in the propositional calculus: in the class-calculus it is false.” Russell then says this about disjunction:
The disjunction is what I shall call a variable disjunction, as opposed to a constant one: that is, in some cases one alternative is true, in others the other, whereas in a constant disjunction there is one of the alternatives (though it is not stated which) that is always true. Wherever disjunctions occur in regard to propositional functions, they will only be transformable into statements in the class-calculus in cases where the disjunction is constant.
Though the vocabulary is unfamiliar, the underlying point is familiar to modern readers, who might put it as follows: a disjunction of
![]() $p \mathbin {\boldsymbol {\vee }} q$
might be such that p is always true, as when p is replaced by ‘
$p \mathbin {\boldsymbol {\vee }} q$
might be such that p is always true, as when p is replaced by ‘
![]() $0=0$
’, or might be such that one of p or q is true, though neither is always true, as when we have p replaced by ‘a is human’ or ‘a is non-human’. The relevance of this passage is that it shows Russell holds that the formal laws in the calculus of classes and those in the calculus of propositions differ. Accordingly, as early as his 1902 manuscripts where ‘
$0=0$
’, or might be such that one of p or q is true, though neither is always true, as when we have p replaced by ‘a is human’ or ‘a is non-human’. The relevance of this passage is that it shows Russell holds that the formal laws in the calculus of classes and those in the calculus of propositions differ. Accordingly, as early as his 1902 manuscripts where ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ is introduced, Russell wants a new symbol to distinguish disjunction and class union.
$\mathbin {\boldsymbol {\vee }}$
’ is introduced, Russell wants a new symbol to distinguish disjunction and class union.
The hypothesis that Russell chose ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ to logically distinguish disjunction as obeying different formal laws, while still preserving its analogy with ‘
$\mathbin {\boldsymbol {\vee }}$
’ to logically distinguish disjunction as obeying different formal laws, while still preserving its analogy with ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’, is further supported by his letter to Frank Morley, the editor of the American Journal of Mathematics, concerning the publication of his 1906 “The Theory of Implication.” The symbol ‘
$\mathrel {\boldsymbol {\cup }}$
’, is further supported by his letter to Frank Morley, the editor of the American Journal of Mathematics, concerning the publication of his 1906 “The Theory of Implication.” The symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ and others were so unfamiliar to Morley that he wrote to Russell about it and noting, perhaps ominously, that authors occasionally had to bear “any heavy expense for new type.” Russell wrote back:
$\mathbin {\boldsymbol {\vee }}$
’ and others were so unfamiliar to Morley that he wrote to Russell about it and noting, perhaps ominously, that authors occasionally had to bear “any heavy expense for new type.” Russell wrote back:
Thank you for your letter. I do not think that any new type ought to be needed, seeing that you have already printed Whitehead’s memoirs. I suppose the sign ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ is doubtful. It is very desirable that it should be pointed, not round; but otherwise it doesn’t matter much whether it is large or small, though I think it would be better small. Of course I will share the expense willingly if it is heavy. (Russell, Reference Russell and Moore2014, p. 15)
$\mathbin {\boldsymbol {\vee }}$
’ is doubtful. It is very desirable that it should be pointed, not round; but otherwise it doesn’t matter much whether it is large or small, though I think it would be better small. Of course I will share the expense willingly if it is heavy. (Russell, Reference Russell and Moore2014, p. 15)
Perhaps we owe to the editorial largess of Morley the modern symbol for disjunction, for, as Russell intimates, ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ does not occur in any of Whitehead’s publications prior to Russell’s 1906 piece. Consequently, one reckons that Morley needed new type (of unknown cost) for ‘
$\mathbin {\boldsymbol {\vee }}$
’ does not occur in any of Whitehead’s publications prior to Russell’s 1906 piece. Consequently, one reckons that Morley needed new type (of unknown cost) for ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’. This amusing episode in the history of ‘
$\mathbin {\boldsymbol {\vee }}$
’. This amusing episode in the history of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ teaches us that editors should not scrimp on notations, and further, that an erstwhile boon of co-authorship was sharing the cost of new type.Footnote
42
$\mathbin {\boldsymbol {\vee }}$
’ teaches us that editors should not scrimp on notations, and further, that an erstwhile boon of co-authorship was sharing the cost of new type.Footnote
42
The crucial point, however, is that Russell expresses to Morley the importance of not printing the disjunction sign as a round symbol. He does not care about its size, but definitely wants it to be pointed. A clear rationale for this is that Russell wants readers to readily distinguish disjunction from class union, a distinction that Russell had been concerned to make going back to Russell (Reference Russell1903c, chap. II). If the exact same sign was used for both, this could confuse the reader concerning the logical distinction between disjunction and union. This is why the size, in contrast, does not matter, so long as the symbol is pointed: it has to be clearly distinguishable on sight from its class theoretic analogue.
The 1906 paper accounts for the first published use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction, but it is worth mentioning that the first unpublished (and so the very first known) systematic uses of ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction, but it is worth mentioning that the first unpublished (and so the very first known) systematic uses of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction (and only for disjunction) occur somewhat earlier in Whitehead and Russell’s writings. Initially, Russell’s practice was the reverse of the modern one: he used the symbol ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction (and only for disjunction) occur somewhat earlier in Whitehead and Russell’s writings. Initially, Russell’s practice was the reverse of the modern one: he used the symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for class union and ‘
$\mathbin {\boldsymbol {\vee }}$
’ for class union and ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ for “propositional addition” (disjunction). In his spring 1902 “On Likeness,” (Russell, Reference Russell1902, p. 440) which was only published after Russell’s death, we find:Footnote
43
$\mathrel {\boldsymbol {\cup }}$
’ for “propositional addition” (disjunction). In his spring 1902 “On Likeness,” (Russell, Reference Russell1902, p. 440) which was only published after Russell’s death, we find:Footnote
43
This definition mashes notation from Peano’s Formulaire with some symbols Russell independently devised in his 1901 “The Logic of Relations” where he insisted on distinguishing relational products and relational intersections (Russell, Reference Russell1901b, p. 315). The key point is that in his 1902 “On Likeness” manuscript, Russell is using the symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for the first time, although not for disjunction. Note that he nonetheless distinguishes propositional disjunction from its analogues for classes and relations. Again, this distinction could be maligned or, as Peano would have it, exploited, but Russell is keen to symbolically separate the two (formally different) notions.
$\mathbin {\boldsymbol {\vee }}$
’ for the first time, although not for disjunction. Note that he nonetheless distinguishes propositional disjunction from its analogues for classes and relations. Again, this distinction could be maligned or, as Peano would have it, exploited, but Russell is keen to symbolically separate the two (formally different) notions.
Russell switches the symbols for disjunction and union in his early 1903 manuscript “Classes,” some of which is now lost. Here we find Russell’s first known use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction (and only for disjunction) (Russell, Reference Russell1903a, p. 9; Figure 2):
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction (and only for disjunction) (Russell, Reference Russell1903a, p. 9; Figure 2):
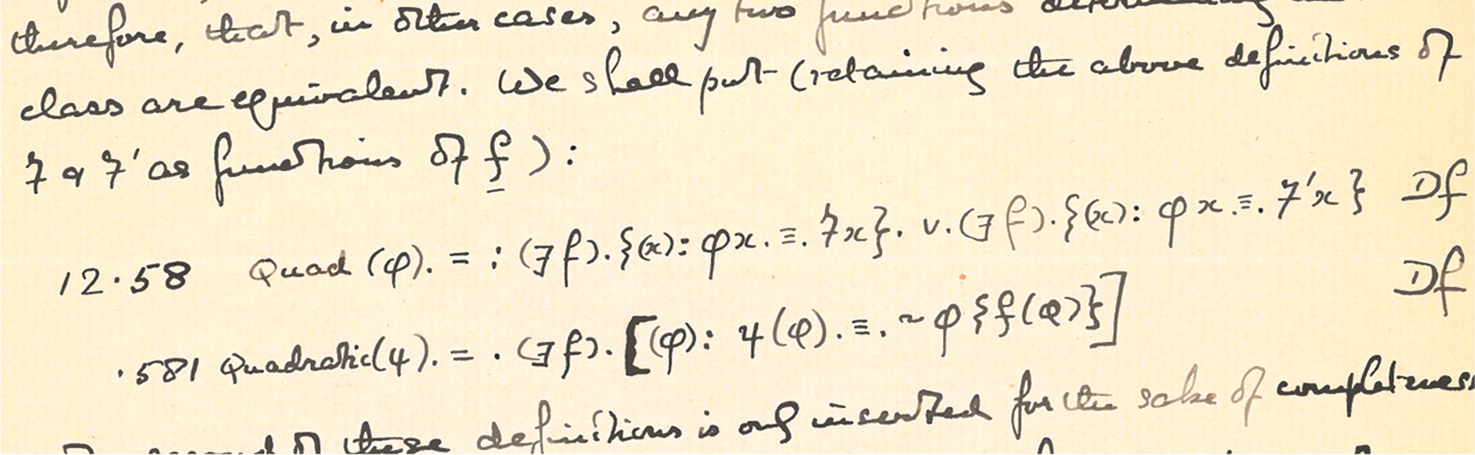
Fig. 2 Use of
![]() $\mathbin {\boldsymbol {\vee }}$
for disjunction in Russell (Reference Russell1903a).
$\mathbin {\boldsymbol {\vee }}$
for disjunction in Russell (Reference Russell1903a).
Comments on a subsequent definition show that Russell here uses ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ only for disjunction:
$\mathbin {\boldsymbol {\vee }}$
’ only for disjunction:
If a and b are classes,
![]() $a\mathrel {\boldsymbol {\cup }} b$
is their logical sum, i.e., the class formed by adding the two. If x is either a member of a or a member of b, then x is a member of
$a\mathrel {\boldsymbol {\cup }} b$
is their logical sum, i.e., the class formed by adding the two. If x is either a member of a or a member of b, then x is a member of
![]() $a\mathrel {\boldsymbol {\cup }} b$
, but not otherwise. The symbol ‘
$a\mathrel {\boldsymbol {\cup }} b$
, but not otherwise. The symbol ‘
![]() $a\mathrel {\boldsymbol {\cup }} b$
’ is read ‘a or b’… The function
$a\mathrel {\boldsymbol {\cup }} b$
’ is read ‘a or b’… The function
![]() $a \mathrel {\boldsymbol {\cup }} b$
is the analogue for classes of
$a \mathrel {\boldsymbol {\cup }} b$
is the analogue for classes of
![]() $p \mathbin {\boldsymbol {\vee }} q$
for propositions. (Russell, Reference Russell1903a, p. 19)
$p \mathbin {\boldsymbol {\vee }} q$
for propositions. (Russell, Reference Russell1903a, p. 19)
Thus, ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction was born in early 1903 (although Russell used it for class union in 1902), and ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction was born in early 1903 (although Russell used it for class union in 1902), and ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction made its first public appearance in April 1906.Footnote
44
This answers the ‘when’ part of question (2). The ‘why’ part, as we saw, stemmed from Russell’s desire to symbolically distinguish class union and propositional disjunction.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction made its first public appearance in April 1906.Footnote
44
This answers the ‘when’ part of question (2). The ‘why’ part, as we saw, stemmed from Russell’s desire to symbolically distinguish class union and propositional disjunction.
There are two complications about this period between Russell’s spring 1902 “On Likeness” (wherein the symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ is first introduced) and the 1903 “Classes” manuscript. First, as was pointed out to us by Urquhart, in a manuscript contemporaneous with the early 1903 “On Classes,” Russell uses ‘
$\mathbin {\boldsymbol {\vee }}$
’ is first introduced) and the 1903 “Classes” manuscript. First, as was pointed out to us by Urquhart, in a manuscript contemporaneous with the early 1903 “On Classes,” Russell uses ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction (and only for disjunction) as well. This manuscript consists of notes Russell made on Frege’s Grundgesetze Vol. II and its attempted solution to the contradiction—hence their title, “Frege on the contradiction.” In one of the last definitions in this manuscript, Russell defines class union using propositional sum, symbolized by ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction (and only for disjunction) as well. This manuscript consists of notes Russell made on Frege’s Grundgesetze Vol. II and its attempted solution to the contradiction—hence their title, “Frege on the contradiction.” In one of the last definitions in this manuscript, Russell defines class union using propositional sum, symbolized by ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ (Figure 3):
$\mathbin {\boldsymbol {\vee }}$
’ (Figure 3):
Urquhart’s dating of this manuscript is supported by a letter that Russell wrote to Frege, dated February 20, 1903, thanking him for sending Volume II of Grundgesetze and asking about its solution to the contradiction. Given the content of these notes, it is likely they were written at nearly the same time as the “On Classes” manuscript. So we strictly speaking have two candidates for the first use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction—and imperfect information as to which one came first!
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction—and imperfect information as to which one came first!
The other complicating factor is that Whitehead also uses ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction (and only for disjunction) in a manuscript that is also from early 1903, “The Logic of Propositional Functions” (Whitehead, Reference Whitehead1903; Figure 4):
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction (and only for disjunction) in a manuscript that is also from early 1903, “The Logic of Propositional Functions” (Whitehead, Reference Whitehead1903; Figure 4):

Fig. 3 Use of
![]() $\mathbin {\boldsymbol {\vee }}$
for disjunction in Russell (Reference Russell1903b).
$\mathbin {\boldsymbol {\vee }}$
for disjunction in Russell (Reference Russell1903b).

Fig. 4 Use of
![]() $\mathbin {\boldsymbol {\vee }}$
for disjunction in Whitehead (Reference Whitehead1903).
$\mathbin {\boldsymbol {\vee }}$
for disjunction in Whitehead (Reference Whitehead1903).
This is a familiar quantification theorem:
(In modern notation:
![]() $\forall x\,\varphi (x) \mathbin {\boldsymbol {\vee }} \forall y\,\psi (y) \mathbin {\boldsymbol {\supset }} \forall x(\varphi (x) \mathbin {\boldsymbol {\vee }} \psi (x))$
). It is not known for certain when this manuscript was written, though the internal evidence suggests it was either late 1902 or early 1903.Footnote
45
Either way, Whitehead’s manuscript dates from after “On Likeness” wherein ‘
$\forall x\,\varphi (x) \mathbin {\boldsymbol {\vee }} \forall y\,\psi (y) \mathbin {\boldsymbol {\supset }} \forall x(\varphi (x) \mathbin {\boldsymbol {\vee }} \psi (x))$
). It is not known for certain when this manuscript was written, though the internal evidence suggests it was either late 1902 or early 1903.Footnote
45
Either way, Whitehead’s manuscript dates from after “On Likeness” wherein ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ is first used by Russell (though not for disjunction). It is difficult beyond that to assign priority for using ‘
$\mathbin {\boldsymbol {\vee }}$
’ is first used by Russell (though not for disjunction). It is difficult beyond that to assign priority for using ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction. The earlier parts of Russell (Reference Russell1903a) were manuscripts on propositional logic and likely included a definition of ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction. The earlier parts of Russell (Reference Russell1903a) were manuscripts on propositional logic and likely included a definition of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ in terms of ‘
$\mathbin {\boldsymbol {\vee }}$
’ in terms of ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ and ‘
$\mathbin {\boldsymbol {\supset }}$
’ and ‘
![]() $\mathord {\boldsymbol {\sim }}$
’. But it is not known whether Whitehead’s or Russell’s manuscript came first. For this reason, we here give joint credit to Whitehead and Russell.Footnote
46
$\mathord {\boldsymbol {\sim }}$
’. But it is not known whether Whitehead’s or Russell’s manuscript came first. For this reason, we here give joint credit to Whitehead and Russell.Footnote
46
Russell’s use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction persists in Russell’s writings and through the 1910 publication of the co-authored Principia. The rest, as they say, is history: the symbol became widely adopted following Principia’s publication. In the next section, we sketch how this state of affairs, which persists today, came about.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction persists in Russell’s writings and through the 1910 publication of the co-authored Principia. The rest, as they say, is history: the symbol became widely adopted following Principia’s publication. In the next section, we sketch how this state of affairs, which persists today, came about.
As a coda to this part of the story, our suggestion that Russell chose ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ as a modification of ‘
$\mathbin {\boldsymbol {\vee }}$
’ as a modification of ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ is further supported by the surprisingly similar genealogy of ‘
$\mathrel {\boldsymbol {\cup }}$
’ is further supported by the surprisingly similar genealogy of ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ and of dots for conjunction. Russell uses ‘
$\mathbin {\boldsymbol {\wedge }}$
’ and of dots for conjunction. Russell uses ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ for the first time in “On Likeness” for class intersection rather than for propositional product, as in the above definition
$\mathbin {\boldsymbol {\wedge }}$
’ for the first time in “On Likeness” for class intersection rather than for propositional product, as in the above definition
![]() . But the story curiously diverges in the 1903 “Classes” manuscript: there Russell introduces ‘
. But the story curiously diverges in the 1903 “Classes” manuscript: there Russell introduces ‘
![]() $\mathbin {\boldsymbol {\wedge }}`m$
’ for a class-operator—the conjunction of a class m of propositions (
$\mathbin {\boldsymbol {\wedge }}`m$
’ for a class-operator—the conjunction of a class m of propositions (
![]() )—and similarly introduces ‘
)—and similarly introduces ‘
![]() $\mathbin {\boldsymbol {\vee }}`m$
’ for its dual class-operator—for the disjunction of a class m of propositions (
$\mathbin {\boldsymbol {\vee }}`m$
’ for its dual class-operator—for the disjunction of a class m of propositions (
![]() ). Despite this, even though Russell also uses ‘
). Despite this, even though Russell also uses ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for propositional disjunction, he uses Peano’s square dots for conjunction as well as scope by 1903. Russell was thus quite close to also giving us ‘
$\mathbin {\boldsymbol {\vee }}$
’ for propositional disjunction, he uses Peano’s square dots for conjunction as well as scope by 1903. Russell was thus quite close to also giving us ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ for conjunction, having used it briefly himself, but chose an alternative.
$\mathbin {\boldsymbol {\wedge }}$
’ for conjunction, having used it briefly himself, but chose an alternative.
Oddly, Russell seems not to have used ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ for conjunction anywhere else. Why did Russell not seize this opportunity? A partial explanation is provided by the fact that the ‘
$\mathbin {\boldsymbol {\wedge }}$
’ for conjunction anywhere else. Why did Russell not seize this opportunity? A partial explanation is provided by the fact that the ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ notation “rarely occurs” (Russell, Reference Russell1903a, p. 20). So the ‘
$\mathbin {\boldsymbol {\wedge }}$
’ notation “rarely occurs” (Russell, Reference Russell1903a, p. 20). So the ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ symbol was not much on Russell’s mind even once he introduced it. Perhaps more importantly, Russell had used dots for conjunction well before he introduced either ‘
$\mathbin {\boldsymbol {\wedge }}$
’ symbol was not much on Russell’s mind even once he introduced it. Perhaps more importantly, Russell had used dots for conjunction well before he introduced either ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ or ‘
$\mathbin {\boldsymbol {\vee }}$
’ or ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’. For example, in his “Logic of Relations” (Russell, Reference Russell1901a) Russell uses dots for conjunction and for scope, reserving concatenation for relational products. In contrast, Peano never used dots for conjunction: he only used dots for scope (Schlimm, Reference Schlimm2021, pp. 118–119). Peano (Reference Peano1895, sec. 1) instead uses concatenation for propositional conjunction and ‘
$\mathbin {\boldsymbol {\wedge }}$
’. For example, in his “Logic of Relations” (Russell, Reference Russell1901a) Russell uses dots for conjunction and for scope, reserving concatenation for relational products. In contrast, Peano never used dots for conjunction: he only used dots for scope (Schlimm, Reference Schlimm2021, pp. 118–119). Peano (Reference Peano1895, sec. 1) instead uses concatenation for propositional conjunction and ‘
![]() $\mathrel {\boldsymbol {\cap }}$
’ for class intersection. So Russell perhaps inserted dots for conjunction to distinguish conjunction from relational products. By the time he thought to use ‘
$\mathrel {\boldsymbol {\cap }}$
’ for class intersection. So Russell perhaps inserted dots for conjunction to distinguish conjunction from relational products. By the time he thought to use ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for anything, he had an established practice of using dots for propositional conjunction. This squeezed out using ‘
$\mathbin {\boldsymbol {\vee }}$
’ for anything, he had an established practice of using dots for propositional conjunction. This squeezed out using ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ for that notion. This episode similarly shows that Russell was keen to introduce new symbols to distinguish logical notions—like propositional and relational “conjunction”—and further supports our hypothesis that this common feature of Russell’s notational design led to introduction of ‘
$\mathbin {\boldsymbol {\wedge }}$
’ for that notion. This episode similarly shows that Russell was keen to introduce new symbols to distinguish logical notions—like propositional and relational “conjunction”—and further supports our hypothesis that this common feature of Russell’s notational design led to introduction of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ rather than any love for Latin or Leibniz.
$\mathbin {\boldsymbol {\vee }}$
’ rather than any love for Latin or Leibniz.
6 The adoption of ‘
 $\boldsymbol \vee $
’
$\boldsymbol \vee $
’
The influence of Principia cemented the use of the Peano–Russell system of symbols among philosophers. This is true first of all of the logicians directly influenced by Principia, including Wittgenstein (Reference Wittgenstein1921) and Ramsey (Reference Ramsey1926). Carnap (Reference Carnap1929), a simplified exposition of the type theory of Principia, uses the same notation, as does Quine (Reference Quine1934). Early philosophy textbooks on logic that adopt a symbolic approach (such as Langer, Reference Langer1937; Lewis, Reference Lewis1918; Nagel & Cohen, Reference Nagel and Cohen1934) also use the symbols of Principia. Notable exceptions, however, are the Polish logicians of the Lwów–Warsaw school, who used Polish notation (usually
![]() $Apq$
for the alternation of p and q).
$Apq$
for the alternation of p and q).
Mathematicians working in the algebra of logic, such as Löwenheim (Reference Löwenheim1915), Skolem (Reference Skolem1920), and Huntington (Reference Huntington1933), continued to use the Boole–Peirce–Schröder notation through the 1930s.Footnote
47
Beginning in the late 1920s, mathematicians more and more converted to the notation made popular by Grundzüge der theoretischen Logik (Hilbert& Ackermann, Reference Hilbert and Ackermann1928): overline for negation, ‘
![]() $\rightarrow $
’ for the material conditional, ‘&’ for conjunction—and ‘
$\rightarrow $
’ for the material conditional, ‘&’ for conjunction—and ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction.
Hilbert and many of his students had mainly relied on Schröder (Reference Schröder1890) as their source of logic, until 1918, when Hilbert tasked Behmann with investigating the new approach to the foundations of mathematics of Principia (see Behmann, Reference Behmann1918; Mancosu, Reference Mancosu1999). In his 1917/18 and 1920 lectures on logic (Reference Behmann1918, Reference Hilbert1920), Hilbert used ‘
![]() $+$
’ and ‘
$+$
’ and ‘
![]() $\times $
’ (or just juxtaposition) for conjunction and disjunction (with overline for negation)—the opposite of the way ‘
$\times $
’ (or just juxtaposition) for conjunction and disjunction (with overline for negation)—the opposite of the way ‘
![]() $+$
’ and ‘
$+$
’ and ‘
![]() $\cdot $
’ are used in the algebraic tradition. Behmann (Reference Behmann1922, Reference Behmann1927) was the only one to use this notation in print.Footnote
48
However, he did this for the specific purpose of logical calculation, where compactness and ease of manipulation are important. He generally endorsed the symbolism of Principia on grounds of uniformity, writing at the beginning of Behmann (Reference Behmann1922),
$\cdot $
’ are used in the algebraic tradition. Behmann (Reference Behmann1922, Reference Behmann1927) was the only one to use this notation in print.Footnote
48
However, he did this for the specific purpose of logical calculation, where compactness and ease of manipulation are important. He generally endorsed the symbolism of Principia on grounds of uniformity, writing at the beginning of Behmann (Reference Behmann1922),
One of the most important requirements for the following investigation is that we provide a suitable symbolism. It may seem to be a given that we should replace the old symbolism of Schröder by the newer one which is currently the most highly regarded and seems to have the best chance of becoming widely adopted, namely the one of Principia Mathematica by Whitehead and Russell.Footnote 49
The treatment of logic in both Hilbert’s lectures and in Behmann’s work is already axiomatic (as in Principia), and not algebraic.
The idiosyncratic notation of 1920 was replaced, in the lecture notes to the 1921/22 course “Foundations of mathematics” (Reference Hilbert1922), by the Hilbert–Ackermann notation, which used the symbols ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’, ‘&’, ‘
$\mathbin {\boldsymbol {\vee }}$
’, ‘&’, ‘
![]() $\to $
’, and overlining for negation. A handwritten note by Bernays in the copy of Hilbert (Reference Hilbert1920) filed in the Göttingen mathematics library, headed “Suggestions for nomenclature [Vorschläge zur Bezeichnung],” reads in part:
$\to $
’, and overlining for negation. A handwritten note by Bernays in the copy of Hilbert (Reference Hilbert1920) filed in the Göttingen mathematics library, headed “Suggestions for nomenclature [Vorschläge zur Bezeichnung],” reads in part:
![]() $X \mathbin {\boldsymbol {\vee }} Y$
: X or Y (abbreviation) (“
$X \mathbin {\boldsymbol {\vee }} Y$
: X or Y (abbreviation) (“
![]() $\mathbin {\boldsymbol {\vee }}$
” is Russell’s symbol, v initial letter of “vel”).Footnote
50
$\mathbin {\boldsymbol {\vee }}$
” is Russell’s symbol, v initial letter of “vel”).Footnote
50
It thus seems likely that the motivation to adopt ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction in the Hilbert school was two-fold: first, to follow Russell’s established usage, and second, because the symbol is reminiscent of vel.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction in the Hilbert school was two-fold: first, to follow Russell’s established usage, and second, because the symbol is reminiscent of vel.
The first use of this system of logical notation in print is in Hilbert (Reference Hilbert1923), and it was adopted in all subsequent publications on logic in Hilbert’s school.Footnote 51 Hilbert & Ackermann (Reference Hilbert and Ackermann1928) proved extremely influential. With it, Hilbert’s way of writing formulas became widely adopted, especially after Gödel (Reference Gödel1930, Reference Gödel1931)—even Skolem used it exclusively from the late 1930s onward (see, e.g., Skolem, Reference Skolem1935).
Tarski was catholic in his use of notations: he used whatever seemed most appropriate. In his dissertation on the logic of Principia, he applied the notation of Principia (Tajtelbaum, Reference Tajtelbaum1923). Writing on propositional calculi with Łukasiewicz, he used Polish notation (Łukasiewicz & Tarski, Reference Łukasiewicz and Tarski1930). Writing for an audience of set theorists, he used algebraic notation (Kuratowski & Tarski, Reference Kuratowski and Tarski1931). Writing for an audience of philosophers (in Erkenntnis, the journal of the Vienna Circle), he used the notation of Principia (Tarski, Reference Tarski1935). And when he wrote for his mathematical colleagues in Vienna (Hahn, Gödel), his logical language used the Hilbert–Ackermann symbols (Tarski, Reference Tarski1933).Footnote 52
Bernays (Reference Bernays1926) mentions that ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ is to have the inclusive meaning of the Latin “vel.” Bernays & Schönfinkel (Reference Bernays and Schönfinkel1928) and Hilbert & Ackermann (Reference Hilbert and Ackermann1928, p. 4) likewise mention this, and also note that ‘
$\mathbin {\boldsymbol {\vee }}$
’ is to have the inclusive meaning of the Latin “vel.” Bernays & Schönfinkel (Reference Bernays and Schönfinkel1928) and Hilbert & Ackermann (Reference Hilbert and Ackermann1928, p. 4) likewise mention this, and also note that ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’—typeset in the latter as a lowercase ‘v’—is not to be confused with exclusive or “in the sense of the Latin ‘aut–aut’.” The identification of vel with inclusive and aut with exclusive or is already made in Schröder (Reference Schröder1890, p. 226), who however used ‘
$\mathbin {\boldsymbol {\vee }}$
’—typeset in the latter as a lowercase ‘v’—is not to be confused with exclusive or “in the sense of the Latin ‘aut–aut’.” The identification of vel with inclusive and aut with exclusive or is already made in Schröder (Reference Schröder1890, p. 226), who however used ‘
![]() $+$
’ and never ‘
$+$
’ and never ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’.Footnote
53
$\mathbin {\boldsymbol {\vee }}$
’.Footnote
53
Quine’s Mathematical logic of 1940 may be the source of the connection between ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ and the initial letter of vel in English textbooks.Footnote
54
He first discusses the exclusive and inclusive use of ‘or’ in English:
$\mathbin {\boldsymbol {\vee }}$
’ and the initial letter of vel in English textbooks.Footnote
54
He first discusses the exclusive and inclusive use of ‘or’ in English:
We must decide whether ‘or’ is to be construed in an exclusive sense, corresponding to the Latin ‘aut’, or in an inclusive sense, corresponding to the Latin ‘vel’. …When ‘or’ is used in the inclusive sense, on the other hand, the compound is regarded as true if at least one of the components is true; joint truth of the components verifies the compound. … In mathematical logic the ambiguity of ordinary usage is resolved by adopting a special symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’, suggestive of ‘vel’, to take the place of ‘or’ in the inclusive sense. Alternation is identified with this usage … The exclusive use of ‘or’ is not frequent enough in technical developments to warrant a special name and symbol. (Quine, Reference Quine1940, pp. 12–13)
$\mathbin {\boldsymbol {\vee }}$
’, suggestive of ‘vel’, to take the place of ‘or’ in the inclusive sense. Alternation is identified with this usage … The exclusive use of ‘or’ is not frequent enough in technical developments to warrant a special name and symbol. (Quine, Reference Quine1940, pp. 12–13)
From Mathematical Logic, the idea that aut and vel in Latin represent the exclusive and inclusive sense of ‘or’, and the use of the symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for the latter, percolates into other introductory logic texts, first Quine’s own Methods of logic:
$\mathbin {\boldsymbol {\vee }}$
’ for the latter, percolates into other introductory logic texts, first Quine’s own Methods of logic:
Latin has distinct words for the two senses of ‘or’: vel for the nonexclusive and aut for the exclusive. In modern logic it is customary to write ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’, reminiscent of vel, for ‘or’ in the nonexclusive sense: ‘
$\mathbin {\boldsymbol {\vee }}$
’, reminiscent of vel, for ‘or’ in the nonexclusive sense: ‘
![]() $p \mathbin {\boldsymbol {\vee }} q$
’. It is this mode of compounding statements, and only this, that is called alternation. (Quine, Reference Quine1950, p. 5)
$p \mathbin {\boldsymbol {\vee }} q$
’. It is this mode of compounding statements, and only this, that is called alternation. (Quine, Reference Quine1950, p. 5)
Quine adds a section on “Alternation and duality” to the revised edition of Elementary logic:
Special symbols are commonly added for ‘or’ and ‘if’. For ‘p or q’ the notation is ‘
![]() $p \mathbin {\boldsymbol {\vee }} q$
’; here ‘
$p \mathbin {\boldsymbol {\vee }} q$
’; here ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ stands for the Latin vel, which means ‘or’ in the inclusive sense. (Quine, Reference Quine1965, p. 52)Footnote
55
$\mathbin {\boldsymbol {\vee }}$
’ stands for the Latin vel, which means ‘or’ in the inclusive sense. (Quine, Reference Quine1965, p. 52)Footnote
55
As we saw above, though, Quine’s alleged connection between ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ and vel is likely spurious: given the textual evidence that we have, the only way this conjecture would hold good would be if Russell saw Peano’s mention of the “
$\mathbin {\boldsymbol {\vee }}$
’ and vel is likely spurious: given the textual evidence that we have, the only way this conjecture would hold good would be if Russell saw Peano’s mention of the “
![]() $\mathbin {\boldsymbol {\vee }}$
is for vel” story about Leibniz and, for that reason, Russell decided to use that notation himself. We argued above that this was a very remote possibility for which there is no surviving evidence, and that there is a highly plausible alternative explanation that fits with a common feature of Whitehead and Russell’s notational design practices.
$\mathbin {\boldsymbol {\vee }}$
is for vel” story about Leibniz and, for that reason, Russell decided to use that notation himself. We argued above that this was a very remote possibility for which there is no surviving evidence, and that there is a highly plausible alternative explanation that fits with a common feature of Whitehead and Russell’s notational design practices.
The work of Whitehead and Russell, and of Hilbert and his students, was defining for the further development of logic in the twentieth century. This gives us an answer to the further question, “why do we (still) use ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’?” The answer is that we have inherited our logical notations from two influential research projects, namely that of Principia and the project of formalizing first-order logic and investigating its properties (completeness, undecidability, etc.) begun by Hilbert. Both of these used ‘
$\mathbin {\boldsymbol {\vee }}$
’?” The answer is that we have inherited our logical notations from two influential research projects, namely that of Principia and the project of formalizing first-order logic and investigating its properties (completeness, undecidability, etc.) begun by Hilbert. Both of these used ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction. Textbook presentations cemented this use further, and Quine’s texts were likely mainly responsible for the spread of the myth that ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction. Textbook presentations cemented this use further, and Quine’s texts were likely mainly responsible for the spread of the myth that ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ abbreviates vel.Footnote
56
$\mathbin {\boldsymbol {\vee }}$
’ abbreviates vel.Footnote
56
7 Other symbols
The symbol ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ is special in that it now is almost universally used for disjunction. But it has been used for other purposes as well; and other symbols also have interesting stories.
$\mathbin {\boldsymbol {\vee }}$
’ is special in that it now is almost universally used for disjunction. But it has been used for other purposes as well; and other symbols also have interesting stories.
Ladd-Franklin (Ladd, Reference Ladd and Peirce1883, pp. 25–26) used ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ and ‘
$\mathbin {\boldsymbol {\vee }}$
’ and ‘
![]() ’ in her dissertation, but only for the copula, that is, for predications among classes and not for propositional connectives. So, Ladd says that ‘
’ in her dissertation, but only for the copula, that is, for predications among classes and not for propositional connectives. So, Ladd says that ‘
![]() $A \mathbin {\boldsymbol {\vee }} B$
’ means “A is in part B,” that is, “some A is B,” and ‘
$A \mathbin {\boldsymbol {\vee }} B$
’ means “A is in part B,” that is, “some A is B,” and ‘
![]() ’ means “A is-not B,” or “No A is B.” The uses of ‘
’ means “A is-not B,” or “No A is B.” The uses of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ and ‘
$\mathbin {\boldsymbol {\vee }}$
’ and ‘
![]() ’ thus correspond to, as Ladd puts it, (Boolean class) “inclusions” and “exclusions” (Ladd, Reference Ladd and Peirce1883, p. 26). She deals, rather, with an analogue of propositional disjunction from a Boolean perspective, where the symbol occurs between categorical terms or concepts rather than between truth-apt formulas.Footnote
57
’ thus correspond to, as Ladd puts it, (Boolean class) “inclusions” and “exclusions” (Ladd, Reference Ladd and Peirce1883, p. 26). She deals, rather, with an analogue of propositional disjunction from a Boolean perspective, where the symbol occurs between categorical terms or concepts rather than between truth-apt formulas.Footnote
57
Tarski (Reference Tarski1933) was one of the first to combine ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ with ‘
$\mathbin {\boldsymbol {\vee }}$
’ with ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ for conjunction. Heyting (Reference Heyting1930) predates this use, however, and is perhaps the first to use ‘
$\mathbin {\boldsymbol {\wedge }}$
’ for conjunction. Heyting (Reference Heyting1930) predates this use, however, and is perhaps the first to use ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ in print as the symbol for conjunction. The first use of ‘
$\mathbin {\boldsymbol {\wedge }}$
’ in print as the symbol for conjunction. The first use of ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ for conjunction in a textbook is probably Tarski (Reference Tarski1941) (the original Polish and German editions did not use logical symbols).
$\mathbin {\boldsymbol {\wedge }}$
’ for conjunction in a textbook is probably Tarski (Reference Tarski1941) (the original Polish and German editions did not use logical symbols).
Sheffer (Reference Sheffer1913) used ‘
![]() $\mathbin {\boldsymbol {\wedge }}$
’ as the symbol for “neither … nor” (nor), i.e., the logical connective corresponding to the operator in Boolean algebra which he symbolized ‘
$\mathbin {\boldsymbol {\wedge }}$
’ as the symbol for “neither … nor” (nor), i.e., the logical connective corresponding to the operator in Boolean algebra which he symbolized ‘
![]() $\boldsymbol \mid $
’. Nicod (Reference Nicod1917) used ‘
$\boldsymbol \mid $
’. Nicod (Reference Nicod1917) used ‘
![]() $\boldsymbol \mid $
’ instead for “not both” (nand), and gave a reduction of the logical constants of Principia to it (the reason being that the resulting definitions of other connectives turn out to be much simpler than with Sheffer’s nor). This has stuck; “Sheffer stroke” now universally means nand. We should point out here, however, that the first published discussion of nand and nor, including proofs that the usual primitives can be expressed by either, and an axiomatization of Boolean algebra in terms of them, is neither Sheffer (Reference Sheffer1913) nor Nicod (Reference Nicod1917), but Stamm (Reference Stamm1911).Footnote
58
$\boldsymbol \mid $
’ instead for “not both” (nand), and gave a reduction of the logical constants of Principia to it (the reason being that the resulting definitions of other connectives turn out to be much simpler than with Sheffer’s nor). This has stuck; “Sheffer stroke” now universally means nand. We should point out here, however, that the first published discussion of nand and nor, including proofs that the usual primitives can be expressed by either, and an axiomatization of Boolean algebra in terms of them, is neither Sheffer (Reference Sheffer1913) nor Nicod (Reference Nicod1917), but Stamm (Reference Stamm1911).Footnote
58
The “neither … nor” connective (nor) is now commonly called the Peirce arrow, and written ‘
![]() $\boldsymbol \downarrow $
’. However, Peirce himself did not use ‘
$\boldsymbol \downarrow $
’. However, Peirce himself did not use ‘
![]() $\boldsymbol \downarrow $
’ for nor, rather, it was introduced by Quine (Reference Quine1940):
$\boldsymbol \downarrow $
’ for nor, rather, it was introduced by Quine (Reference Quine1940):
The fact that
![]() denies
denies
![]() $\ulcorner (\phi \mathbin {\boldsymbol {\vee }} \psi )\urcorner $
is reflected in ordinary language, indeed, by the cancellatory ‘n’ which turns ‘either—or’ into ‘neither—nor’. The vertical mark in ‘
$\ulcorner (\phi \mathbin {\boldsymbol {\vee }} \psi )\urcorner $
is reflected in ordinary language, indeed, by the cancellatory ‘n’ which turns ‘either—or’ into ‘neither—nor’. The vertical mark in ‘
![]() ’ may be thought of as having the same cancellatory effect upon the sign ‘
’ may be thought of as having the same cancellatory effect upon the sign ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’; it is like the vertical mark in the inequality sign ‘
$\mathbin {\boldsymbol {\vee }}$
’; it is like the vertical mark in the inequality sign ‘
![]() ’ of arithmetic. (p. 46)
’ of arithmetic. (p. 46)
Although Quine himself does not call his ‘
![]() ’ the ‘Peirce arrow’, he does credit Peirce for his work on it in footnote 1 on page 49:
’ the ‘Peirce arrow’, he does credit Peirce for his work on it in footnote 1 on page 49:
The definability of denial, conjunction, and alternation in terms of joint denial [nor, the Peirce arrow] was first pointed out by Sheffer (Reference Sheffer1913); and similarly for alternative denial [nand, the Sheffer stroke]. The adequacy of joint denial was known to Peirce in 1880, and both facts were known to him in 1902; but his notes on the subject remained unpublished until Reference Peirce1933 (4.12, 4.264).
As Quine remarks, Peirce’s writings on nor had only recently become available. In the manuscripts mentioned by Quine, Peirce first simply used juxtaposition: “Two propositions written in a pair are considered both denied. Thus,
![]() $AB$
means that the propositions A and B are both false” (Peirce Reference Peirce1880, p. 13). In Peirce (Reference Peirce1902), he introduced the symbol ‘
$AB$
means that the propositions A and B are both false” (Peirce Reference Peirce1880, p. 13). In Peirce (Reference Peirce1902), he introduced the symbol ‘
![]() ’, which he called “ampheck” (p. 215).
’, which he called “ampheck” (p. 215).
Quine (Reference Quine1940) also gave an origin story for ‘
![]() $\sim $
’:Footnote
59
$\sim $
’:Footnote
59
In mathematical logic the denial of a statement is formed by prefixing the tilde ‘
![]() $\sim $
’, which is a modified ‘n’ and is conveniently read ‘not’. (p. 14)
$\sim $
’, which is a modified ‘n’ and is conveniently read ‘not’. (p. 14)
The history recounted in this paper shows that we should be wary of just-so stories about the origins of notations like Quine tells here. If we had to make a conjecture, we would agree with Moore (Reference Moore2014, p. lxi) that Russell began using a tilde for negation for reasons that conform to his well-attested to practice of distinguishing different notions in his symbolism whenever the formal laws differed, so that ‘
![]() $\mathord {\boldsymbol {\sim }}$
’ was introduced to distinguish propositional negation from class (or arithmetic) subtraction.
$\mathord {\boldsymbol {\sim }}$
’ was introduced to distinguish propositional negation from class (or arithmetic) subtraction.
The two standard symbols for the material conditional (implication) are ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ and ‘
$\mathbin {\boldsymbol {\supset }}$
’ and ‘
![]() $\to $
’. The latter, as noted above, was introduced by Hilbert (Reference Hilbert1918, Reference Hilbert1920) and become widely adopted after it was used in the influential Grundzüge textbook (Hilbert & Ackermann, Reference Hilbert and Ackermann1928). The origin of ‘
$\to $
’. The latter, as noted above, was introduced by Hilbert (Reference Hilbert1918, Reference Hilbert1920) and become widely adopted after it was used in the influential Grundzüge textbook (Hilbert & Ackermann, Reference Hilbert and Ackermann1928). The origin of ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ is a bit more complicated: Peano introduced ‘
$\mathbin {\boldsymbol {\supset }}$
’ is a bit more complicated: Peano introduced ‘
![]() ’ as a symbol for both the conditional and for class containment, as the rotated version of ‘c’, abbreviating “est consequentia” and “continet,” Latin for “is a consequence of” and “contains”:
’ as a symbol for both the conditional and for class containment, as the rotated version of ‘c’, abbreviating “est consequentia” and “continet,” Latin for “is a consequence of” and “contains”:
[The sign c means is a consequence of; thus
![]() is read b is a consequence of the proposition a. But we never use this sign.]
is read b is a consequence of the proposition a. But we never use this sign.]
The sign
![]() means one deduces; thus
means one deduces; thus
![]() means the same as
means the same as
![]() .Footnote
60
.Footnote
60
The sign
![]() means is contained. Thus
means is contained. Thus
![]() means the class a is contained in the class b. …The signs
means the class a is contained in the class b. …The signs
![]() $\Lambda $
and
$\Lambda $
and
![]() have meanings here which are slightly different from the preceding, but no ambiguity will arise, for if propositions are being considered, the signs are read absurd and one deduces, but if classes are being considered, they are read empty and is contained.Footnote
61
have meanings here which are slightly different from the preceding, but no ambiguity will arise, for if propositions are being considered, the signs are read absurd and one deduces, but if classes are being considered, they are read empty and is contained.Footnote
61
Beginning with Peano (Reference Peano1898), the symbol ‘
![]() ’ is replaced with ‘
’ is replaced with ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ but with the same ambiguous use.Footnote
62
Russell of course derived his ‘
$\mathbin {\boldsymbol {\supset }}$
’ but with the same ambiguous use.Footnote
62
Russell of course derived his ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ from Peano and used it as early as Russell (Reference Russell1901a). This was a French translation of a 1900 manuscript (Russell, Reference Russell1900b), published in Peano’s Revue de mathématiques. Therein the symbol was typeset interchangeably as ‘
$\mathbin {\boldsymbol {\supset }}$
’ from Peano and used it as early as Russell (Reference Russell1901a). This was a French translation of a 1900 manuscript (Russell, Reference Russell1900b), published in Peano’s Revue de mathématiques. Therein the symbol was typeset interchangeably as ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’ and as ‘
$\mathbin {\boldsymbol {\supset }}$
’ and as ‘
![]() ’.Footnote
63
Later, including in Principia, Russell had it typeset as ‘
’.Footnote
63
Later, including in Principia, Russell had it typeset as ‘
![]() $\mathbin {\boldsymbol {\supset }}$
’.
$\mathbin {\boldsymbol {\supset }}$
’.
8 Conclusion
Logicians and historians of logic have suggested various origin stories for ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ as the symbol for disjunction. As we saw above, Peano suggests that Leibniz chose ‘
$\mathbin {\boldsymbol {\vee }}$
’ as the symbol for disjunction. As we saw above, Peano suggests that Leibniz chose ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for the Latin vel. Kneale and Kneale suggest that Peano first chose it. Cajori attributes the first use to Principia. According to Quine, ‘
$\mathbin {\boldsymbol {\vee }}$
’ for the Latin vel. Kneale and Kneale suggest that Peano first chose it. Cajori attributes the first use to Principia. According to Quine, ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ stands for, or at least suggests, the Latin vel. The evidence discussed in this paper indicates that ‘
$\mathbin {\boldsymbol {\vee }}$
’ stands for, or at least suggests, the Latin vel. The evidence discussed in this paper indicates that ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction is not a straightforward Latin abbreviation, and that logicians and historians of logic have often attributed the first use of ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction is not a straightforward Latin abbreviation, and that logicians and historians of logic have often attributed the first use of ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction to the wrong author or to the wrong text.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction to the wrong author or to the wrong text.
The appealing story often told that our ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction comes from the Latin vel is not well-supported by the textual record. It was Whitehead and Russell who first systematically used ‘
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction comes from the Latin vel is not well-supported by the textual record. It was Whitehead and Russell who first systematically used ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction, and it is more likely given Whitehead and Russell’s notational habits (and Russell’s disgust for Latin) that this choice of notation was to stress the analogy of propositional addition with class union.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction, and it is more likely given Whitehead and Russell’s notational habits (and Russell’s disgust for Latin) that this choice of notation was to stress the analogy of propositional addition with class union.
This may all seem like nothing more than logical Trivial Pursuit. However, our discussion also highlights features of the trajectory of the development of logical notations that is not trivial. We have seen that the considerations for or against the choice of a symbol used for ‘or’ were often deeper than just whether or not it serves as a good mnemonic device (a symbol reminiscent of vel). The mathematical tradition of the algebra of logic stressed the similarity of class union and propositional (or truth-value) disjunction with algebraic operations, and thus often chose the same symbols used in algebra (‘
![]() $+$
’ or ‘
$+$
’ or ‘
![]() $\times $
’). Other writers were concerned with separating arithmetical or algebraic notations (or defining them) from more general logical notations. This, e.g., led Peano to use a different symbol for (logical) union and disjunction than the algebraic ‘
$\times $
’). Other writers were concerned with separating arithmetical or algebraic notations (or defining them) from more general logical notations. This, e.g., led Peano to use a different symbol for (logical) union and disjunction than the algebraic ‘
![]() $+$
’, and it led Whitehead and Russell to use distinct symbols for class union and propositional disjunction. These concerns for mathematical uniformity and philosophically relevant distinctions, of course, extend to symbols and notions other than “or.”
$+$
’, and it led Whitehead and Russell to use distinct symbols for class union and propositional disjunction. These concerns for mathematical uniformity and philosophically relevant distinctions, of course, extend to symbols and notions other than “or.”
The story connects with other important concerns that influenced the development of a system of notation which, since Cajori penned the passage we opened the paper with, has become almost standardized. These include the motivations for choosing the particular set of primitives that have become commonplace, e.g., why we take inclusive and not exclusive disjunction as a primitive. It also connects with the question of why and when different approaches to logic (and notation) became more widespread or lost appeal: the choice of notations of the pioneering writers of the early to mid-twentieth century provides insight into their influences and methodological commitments. We have only touched upon these deeper topics, but they suggest fruitful directions for further research.
If nothing else, we now have an answer to the question: “Why
![]() $\mathbin {\boldsymbol {\vee }}$
?” We owe it to Whitehead and Russell, who in spring 1902 wanted a symbol different from Peano’s (and Grassmann’s) symbol ‘
$\mathbin {\boldsymbol {\vee }}$
?” We owe it to Whitehead and Russell, who in spring 1902 wanted a symbol different from Peano’s (and Grassmann’s) symbol ‘
![]() $\mathrel {\boldsymbol {\cup }}$
’ to distinguish union and propositional disjunction in his symbolism. After, and in part because Hilbert endorsed Whitehead and Russell’s choice to use ‘
$\mathrel {\boldsymbol {\cup }}$
’ to distinguish union and propositional disjunction in his symbolism. After, and in part because Hilbert endorsed Whitehead and Russell’s choice to use ‘
![]() $\mathbin {\boldsymbol {\vee }}$
’ for disjunction in Principia, the symbol became ubiquitous.
$\mathbin {\boldsymbol {\vee }}$
’ for disjunction in Principia, the symbol became ubiquitous.
Acknowledgments
We thank the hosts Alexander Klein and Sandra Lapointe as well as the participants of the Fall 2020 Bertrand Russell Research Centre and Journal of the History of Analytical Philosophy graduate seminar, who raised insightful questions and gave helpful comments. The paper was also discussed with the History and Philosophy of Mathematics Reading Group at McGill University, and we especially thank Moritz Bodner, Julien Ouellette-Michaud, David Waszek, and Dirk Schlimm for their questions and suggestions. We are also grateful to Katalin Bimbó, Edward Buckney, Bernard Linsky, Paolo Mancosu, Marcus Rossberg, Sara L. Uckelman, Rafał Urbaniak, and especially Massimo Mugnai, Brent Odland, Alasdair Urquhart, Jack Zupko, and the reviewer for the RSL, all of whose suggestions and comments improved the manuscript. We’d also like to acknowledge the Bertrand Russell Archives at McMaster University and the Gottfried Wilhelm Leibniz Bibliothek for providing scans of the Whitehead, Russell, and Leibniz manuscripts. Much of this research was done while Elkind was a Killam Postdoctoral Fellow at the University of Alberta. Elkind thanks the Killam Trusts for their support. The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Program.
















