No CrossRef data available.
Published online by Cambridge University Press: 08 June 2018
Abstract algebraic logic is a theory that provides general tools for the algebraic study of arbitrary propositional logics. According to this theory, every logic 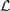 ${\cal L}$ is associated with a matrix semantics
${\cal L}$ is associated with a matrix semantics  $Mo{d^{\rm{*}}}{\cal L}$. This article is a contribution to the systematic study of the so-called truth sets of the matrices in
$Mo{d^{\rm{*}}}{\cal L}$. This article is a contribution to the systematic study of the so-called truth sets of the matrices in 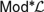 $Mo{d^{\rm{*}}}{\cal L}$. In particular, we show that the fact that the truth sets of
$Mo{d^{\rm{*}}}{\cal L}$. In particular, we show that the fact that the truth sets of 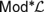 $Mo{d^{\rm{*}}}{\cal L}$ can be defined by means of equations with universally quantified parameters is captured by an order-theoretic property of the Leibniz operator restricted to deductive filters of
$Mo{d^{\rm{*}}}{\cal L}$ can be defined by means of equations with universally quantified parameters is captured by an order-theoretic property of the Leibniz operator restricted to deductive filters of 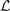 ${\cal L}$. This result was previously known for equational definability without parameters. Similarly, it was known that the truth sets of
${\cal L}$. This result was previously known for equational definability without parameters. Similarly, it was known that the truth sets of 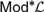 $Mo{d^{\rm{*}}}{\cal L}$ are implicitly definable if and only if the Leibniz operator is injective on deductive filters of
$Mo{d^{\rm{*}}}{\cal L}$ are implicitly definable if and only if the Leibniz operator is injective on deductive filters of 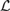 ${\cal L}$ over every algebra. However, it was an open problem whether the injectivity of the Leibniz operator transfers from the theories of
${\cal L}$ over every algebra. However, it was an open problem whether the injectivity of the Leibniz operator transfers from the theories of 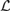 ${\cal L}$ to its deductive filters over arbitrary algebras. We show that this is the case for logics expressed in a countable language, and that it need not be true in general. Finally we consider an intermediate condition on the truth sets in
${\cal L}$ to its deductive filters over arbitrary algebras. We show that this is the case for logics expressed in a countable language, and that it need not be true in general. Finally we consider an intermediate condition on the truth sets in 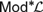 $Mo{d^{\rm{*}}}{\cal L}$ that corresponds to the order-reflection of the Leibniz operator.
$Mo{d^{\rm{*}}}{\cal L}$ that corresponds to the order-reflection of the Leibniz operator.