Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Salomaa, Arto
Salomaa, Kai
and
Yu, Sheng
2007.
State complexity of combined operations.
Theoretical Computer Science,
Vol. 383,
Issue. 2-3,
p.
140.
Holzer, Markus
and
Kutrib, Martin
2008.
Implementation and Applications of Automata.
Vol. 5148,
Issue. ,
p.
1.
Brzozowski, Janusz
2009.
Quotient Complexity of Regular Languages.
Electronic Proceedings in Theoretical Computer Science,
Vol. 3,
Issue. ,
p.
17.
HOLZER, MARKUS
and
KUTRIB, MARTIN
2009.
NONDETERMINISTIC FINITE AUTOMATA — RECENT RESULTS ON THE DESCRIPTIONAL AND COMPUTATIONAL COMPLEXITY.
International Journal of Foundations of Computer Science,
Vol. 20,
Issue. 04,
p.
563.
Jirásková, Galina
and
Okhotin, Alexander
2009.
Nondeterministic State Complexity of Positional Addition.
Electronic Proceedings in Theoretical Computer Science,
Vol. 3,
Issue. ,
p.
151.
Gruber, Hermann
and
Holzer, Markus
2009.
Language operations with regular expressions of polynomial size.
Theoretical Computer Science,
Vol. 410,
Issue. 35,
p.
3281.
Jirásková, Galina
and
Krausová, Monika
2010.
Complexity in Prefix-Free Regular Languages.
Electronic Proceedings in Theoretical Computer Science,
Vol. 31,
Issue. ,
p.
197.
Jirásková, Galina
and
Masopust, Tomáš
2010.
Developments in Language Theory.
Vol. 6224,
Issue. ,
p.
255.
JIRÁSKOVÁ, GALINA
and
MASOPUST, TOMÁŠ
2011.
COMPLEXITY IN UNION-FREE REGULAR LANGUAGES.
International Journal of Foundations of Computer Science,
Vol. 22,
Issue. 07,
p.
1639.
Jirásková, Galina
and
Masopust, Tomáš
2012.
Theoretical Computer Science.
Vol. 7604,
Issue. ,
p.
164.
Bianchi, Maria Paola
Holzer, Markus
Jakobi, Sebastian
and
Pighizzini, Giovanni
2012.
Descriptional Complexity of Formal Systems.
Vol. 7386,
Issue. ,
p.
89.
Cui, Bo
Gao, Yuan
Kari, Lila
and
Yu, Sheng
2012.
State complexity of combined operations with two basic operations.
Theoretical Computer Science,
Vol. 437,
Issue. ,
p.
82.
Jirásek, Jozef
and
Jirásková, Galina
2013.
Computer Science – Theory and Applications.
Vol. 7913,
Issue. ,
p.
246.
Čevorová, Kristína
Jirásková, Galina
Mlynárčik, Peter
Palmovský, Matúš
and
Šebej, Juraj
2014.
Operations on Automata with All States Final.
Electronic Proceedings in Theoretical Computer Science,
Vol. 151,
Issue. ,
p.
201.
Davies, Sylvie
2018.
Developments in Language Theory.
Vol. 11088,
Issue. ,
p.
256.
Okhotin, Alexander
and
Salomaa, Kai
2019.
Further closure properties of input-driven pushdown automata.
Theoretical Computer Science,
Vol. 798,
Issue. ,
p.
65.
Caron, Pascal
Hamel-de le Court, Edwin
and
Luque, Jean-Gabriel
2019.
Algebraic and Combinatorial Tools for State Complexity : Application to the Star-Xor Problem.
Electronic Proceedings in Theoretical Computer Science,
Vol. 305,
Issue. ,
p.
154.
Gabric, Daniel
Holub, Štěpán
and
Shallit, Jeffrey
2019.
Descriptional Complexity of Formal Systems.
Vol. 11612,
Issue. ,
p.
137.
Hospodár, Michal
and
Mlynárčik, Peter
2020.
Developments in Language Theory.
Vol. 12086,
Issue. ,
p.
122.
Okhotin, Alexander
and
Sorokin, Alexey
2020.
Language and Automata Theory and Applications.
Vol. 12038,
Issue. ,
p.
287.
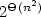 state complexity.
We also establish a tight 2n2+1 lower bound for
the nondeterministic state complexity of this operation using a binary alphabet.
state complexity.
We also establish a tight 2n2+1 lower bound for
the nondeterministic state complexity of this operation using a binary alphabet.