Published online by Cambridge University Press: 15 April 2002
We investigate the complexity of languages described by some expressions
containing shuffle operator and intersection. We show that deciding whether
the shuffle of two words has a nonempty intersection with a regular set
(or fulfills some regular pattern) is NL-complete.
Furthermore we show that the class of languages of the form $L\cap R$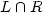 ,
with a shuffle language L and a regular language R, contains
non-semilinear languages and does not form a family of mildly
context- sensitive languages.
,
with a shuffle language L and a regular language R, contains
non-semilinear languages and does not form a family of mildly
context- sensitive languages.