Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
EL Ghami, M.
Bai, Y. Q.
and
Roos, C.
2009.
Kernel-function Based Algorithms for Semidefinite Optimization.
RAIRO - Operations Research,
Vol. 43,
Issue. 2,
p.
189.
CHO, G. M.
CHO, Y. Y.
and
LEE, Y. H.
2010.
A PRIMAL-DUAL INTERIOR-POINT ALGORITHM BASED ON A NEW KERNEL FUNCTION.
The ANZIAM Journal,
Vol. 51,
Issue. 4,
p.
476.
Cho, Gyeong-Mi
2011.
An interior-point algorithm for linear optimization based on a new barrier function.
Applied Mathematics and Computation,
Vol. 218,
Issue. 2,
p.
386.
Vieira, Manuel V. C.
2012.
The Accuracy of Interior-Point Methods Based on Kernel Functions.
Journal of Optimization Theory and Applications,
Vol. 155,
Issue. 2,
p.
637.
El Ghami, M.
Guennoun, Z.A.
Bouali, S.
and
Steihaug, T.
2012.
Interior-point methods for linear optimization based on a kernel function with a trigonometric barrier term.
Journal of Computational and Applied Mathematics,
Vol. 236,
Issue. 15,
p.
3613.
Cai, Xinzhong
Wu, Lin
Yue, Yujing
Li, Minmin
and
Wang, Guoqiang
2014.
Kernel-function-based primal-dual interior-point methods for convex quadratic optimization over symmetric cone.
Journal of Inequalities and Applications,
Vol. 2014,
Issue. 1,
Peyghami, M. Reza
Hafshejani, S. Fathi
and
Shirvani, L.
2014.
Complexity of interior-point methods for linear optimization based on a new trigonometric kernel function.
Journal of Computational and Applied Mathematics,
Vol. 255,
Issue. ,
p.
74.
Peyghami, M. Reza
and
Hafshejani, S. Fathi
2014.
Complexity analysis of an interior-point algorithm for linear optimization based on a new proximity function.
Numerical Algorithms,
Vol. 67,
Issue. 1,
p.
33.
Bouafia, Mousaab
Benterki, Djamel
and
Yassine, Adnan
2015.
Modelling, Computation and Optimization in Information Systems and Management Sciences.
Vol. 359,
Issue. ,
p.
357.
Hafshejani, S. Fathi
Fatemi, M.
and
Peyghami, M. Reza
2015.
An interior-point method for $$P_*(\kappa )$$ P ∗ ( κ ) -linear complementarity problem based on a trigonometric kernel function.
Journal of Applied Mathematics and Computing,
Vol. 48,
Issue. 1-2,
p.
111.
Touil, Imene
Chikouche, Wided
Benterki, Djamel
and
Zerari, Amina
2025.
An Efficient Hyperbolic Kernel Function Yielding the Best Known Iteration Bounds for Linear Programming.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 41,
Issue. 1,
p.
133.
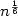 when compared with the method based on the use of the classical logarithmic barrier function. For small-update interior point methods the iteration bound is $O(\sqrt{n}\log\frac{n}{\epsilon}),$
when compared with the method based on the use of the classical logarithmic barrier function. For small-update interior point methods the iteration bound is $O(\sqrt{n}\log\frac{n}{\epsilon}),$ 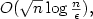 which is currently the best-known bound for primal-dual IPMs.
which is currently the best-known bound for primal-dual IPMs.
