Article contents
Computational schemes for two exponential servers where the first has a finite buffer
Published online by Cambridge University Press: 10 May 2011
Abstract
We consider a system consisting of two not necessarily identicalexponential servers having a common Poisson arrival process. Uponarrival, customers inspect the first queue and join it if it isshorter than some threshold n. Otherwise, they join the secondqueue. This model was dealt with, among others, by Altman et al. [Stochastic Models 20 (2004) 149–172].We first derive an explicitexpression for the Laplace-Stieltjes transform of the distributionunderlying the arrival (renewal) process to the second queue. Second,we observe that given that the second serveris busy, the two queue lengths are independent.Third, we develop two computational schemes for thestationary distribution of the two-dimensional Markov process underlying thismodel, one with a complexity of$O(n \log\delta^{-1})$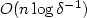 , the other with a complexity of $O(\log n\log^2\delta^{-1})$
, the other with a complexity of $O(\log n\log^2\delta^{-1})$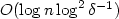 , where δ is the tolerance criterion.
, where δ is the tolerance criterion.
Information
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, ROADEF, SMAI, 2011
References
- 6
- Cited by

