Introduction
Single molecules (SMs) have emerged as powerful, noninvasive probes for studies spanning biology, biochemistry, biophysics, and material science (Metskas and Rhoades, Reference Metskas and Rhoades2020; Möckl and Moerner, Reference Möckl and Moerner2020; Lelek et al., Reference Lelek, Gyparaki, Beliu, Schueder, Griffié, Manley, Jungmann, Sauer, Lakadamyali and Zimmer2021; Bustamante et al., Reference Bustamante, Chemla, Liu and Wang2021) since they were first observed using optical methods over three decades ago (Moerner and Kador, Reference Moerner and Kador1989; Betzig and Chichester, Reference Betzig and Chichester1993; Xie, Reference Xie1996). Their capability to discern and quantify intricate nanoscale processes at the molecular level continues to drive innovation in the field of microscopy. Over the last few decades, single-molecule localization microscopy (SMLM) (Betzig et al., Reference Betzig, Patterson, Sougrat, Lindwasser, Olenych, Bonifacino, Davidson, Lippincott-Schwartz and Hess2006; Hess et al., Reference Hess, Girirajan and Mason2006; Rust et al., Reference Rust, Bates and Zhuang2006; Sharonov and Hochstrasser, Reference Sharonov and Hochstrasser2006) has revolutionized our ability to visualize cellular structures with unprecedented resolution surpassing the Abbé diffraction limit of ~250 nm. These techniques leverage the active control of fluorescence “on–off” states to reduce the concentration of emitting molecules, precisely localize the SMs, and reconstruct an image of the underlying structure with a typical resolution on the order of 10 nanometers (Moerner, Reference Moerner2015). During the past two decades, the field continues to innovate with sequential (Reinhardt et al., Reference Reinhardt, Masullo, Baudrexel, Steen, Kowalewski, Eklund, Strauss, Unterauer, Schlichthaerle, Strauss, Klein and Jungmann2023), energy-transfer (Ghosh et al., Reference Ghosh, Sharma, Chizhik, Isbaner, Ruhlandt, Tsukanov, Gregor, Karedla and Enderlein2019; Hauke et al., Reference Hauke, Isbaner, Ghosh, Guido, Turco, Chizhik, Gregor, Karedla, Rehfeldt and Enderlein2023; Chen et al., Reference Chen, Karedla and Enderlein2024a), interferometric (Shtengel et al., Reference Shtengel, Galbraith, Galbraith, Lippincott-Schwartz, Gillette, Manley, Sougrat, Waterman, Kanchanawong, Davidson, Fetter and Hess2009; Aquino et al., Reference Aquino, Schönle, Geisler, Middendorff, Wurm, Okamura, Lang, Hell and Egner2011; Huang et al., Reference Huang, Sirinakis, Allgeyer, Schroeder, Duim, Kromann, Phan, Rivera-Molina, Myers, Irnov, Lessard, Zhang, Handel, Jacobs-Wagner, Lusk, Rothman, Toomre, Booth and Bewersdorf2016), and adaptive (Balzarotti et al., Reference Balzarotti, Eilers, Gwosch, Gynnå, Westphal, Stefani, Elf and Hell2017; Cnossen et al., Reference Cnossen, Hinsdale, Thorsen, Siemons, Schueder, Jungmann, Smith, Rieger and Stallinga2020; Gwosch et al., Reference Gwosch, Pape, Balzarotti, Hoess, Ellenberg, Ries and Hell2020; Weber et al., Reference Weber, Von Der Emde, Leutenegger, Gunkel, Sambandan, Khan, Keller-Findeisen, Cordes and Hell2023; Sahl et al., Reference Sahl, Matthias, Inamdar, Weber, Khan, Brüser, Jakobs, Becker, Griesinger, Broichhagen and Hell2024) imaging techniques, pushing practical localization precision to the molecular scale (<1 nm).
In the decade since the Nobel Prize in Chemistry 2014, developments have shifted toward functional imaging, i.e., sophisticated methods capable of imaging physicochemical properties beyond where molecules are located (Steves et al., Reference Steves, He and Xu2024). Examples include measuring the emission spectrum (Zhang et al., Reference Zhang, Kenny, Hauser, Li and Xu2015; Bongiovanni et al., Reference Bongiovanni, Godet, Horrocks, Tosatto, Carr, Wirthensohn, Ranasinghe, Lee, Ponjavic, Fritz, Dobson, Klenerman and Lee2016; Brenner et al., Reference Brenner, Sun, Raymo and Zhang2023), fluorescence lifetime (Thiele et al., Reference Thiele, Helmerich, Oleksiievets, Tsukanov, Butkevich, Sauer, Nevskyi and Enderlein2020; Oleksiievets et al., Reference Oleksiievets, Mathew, Thiele, Gallea, Nevskyi, Gregor, Weber, Tsukanov and Enderlein2022), and orientation and rotational diffusion, i.e., “wobble,” (Backlund et al., Reference Backlund, Lew, Backer, Sahl and Moerner2014; Valades Cruz et al., Reference Valades Cruz, Shaban, Kress, Bertaux, Monneret, Mavrakis, Savatier and Brasselet2016; Shaban et al., Reference Shaban, Valades-Cruz, Savatier and Brasselet2017) of individual molecules. Methods that simultaneously image molecular positions and orientations, termed single-molecule orientation-localization microscopy (SMOLM), have been shown to improve localization accuracy in SMLM since changes in orientation can be mistakenly perceived as changes in molecular position (Engelhardt et al., Reference Engelhardt, Keller, Hoyer, Reuss, Staudt and Hell2011; Backlund et al., Reference Backlund, Lew, Backer, Sahl, Grover, Agrawal, Piestun and Moerner2012, Reference Backlund, Lew, Backer, Sahl and Moerner2014; Lew and Moerner, Reference Lew and Moerner2014; Backlund et al., Reference Backlund, Arbabi, Petrov, Arbabi, Saurabh, Faraon and Moerner2016). Moreover, SMOLM offers profound insights into molecular structures and dynamics at the nanoscale that cannot be resolved in SMLM, such as the organization of amyloid aggregates (Shaban et al., Reference Shaban, Valades-Cruz, Savatier and Brasselet2017; Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020; Ding and Lew, Reference Ding and Lew2021; Zhou et al., Reference Zhou, O’Neill, Ding, Zhang, Rudra and Lew2024a; Sun et al., Reference Sun, Ding, Zhou, Porter and Lew2024), conformations of DNA strands (Ha et al., Reference Ha, Enderle, Chemla, Selvin and Weiss1996, Reference Ha, Glass, Th, Chemla and Weiss1998; Backer et al., Reference Backer, Lee and Moerner2016, Reference Backer, Biebricher, King, Wuite, Heller and Peterman2019; Mazidi et al., Reference Mazidi, King, Zhang, Nehorai and Lew2019; Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021), structure of actin networks (Valades Cruz et al., Reference Valades Cruz, Shaban, Kress, Bertaux, Monneret, Mavrakis, Savatier and Brasselet2016; Curcio et al., Reference Curcio, Alemán-Castañeda, Brown, Brasselet and Alonso2020; Rimoli et al., Reference Rimoli, Valades-Cruz, Curcio, Mavrakis and Brasselet2022), and the dynamic movements of molecular motors (Sosa et al., Reference Sosa, Peterman, Moerner and Goldstein2001; Peterman et al., Reference Peterman, Sosa, Goldstein and Moerner2001; Forkey et al., Reference Forkey, Quinlan, Alexander Shaw, Corrie and Goldman2003; Beausang et al., Reference Beausang, Shroder, Nelson and Goldman2013; Lippert et al., Reference Lippert, Dadosh, Hadden, Karnawat, Diroll, Murray, Holzbaur, Schulten, Reck-Peterson and Goldman2017).
In a typical SMOLM experiment, the target is labeled with fluorescent probes whose orientations convey useful information. Importantly, the fluorescent probe and labeling method must be chosen carefully. For example, a rigid bifunctional attachment strategy useful for probing the rotational motions of molecular motors is unlikely to be adaptable for characterizing the conformations of disordered proteins. In addition, fluorogenic “turn-on” probes, in contrast to conventional fluorophores, offer a degree of environmental sensitivity that can synergistically complement the orientational data measured by SMOLM.
The emitted fluorescence is then collected and modulated by an imaging system, and images are captured using photon-counting cameras. Since a standard fluorescence microscope has poor sensitivity for measuring molecular orientation, it must be modified to measure fluorescence emission under varying pumping polarization, manipulate the polarization and/or phase of the fluorescence emission, or both. These advancements, combined with algorithms capable of detecting dim fluorescent emitters and robustly estimating 2D/3D position and 2D/3D orientation simultaneously, are essential to quantify the rotational dynamics of SMs precisely and accurately.
In this review, we discuss new developments in these aspects of SMOLM and organize our coverage as follows. (Techniques that used polarized light to measure micro- and mesoscale biological structures are covered excellently elsewhere (Alonso, Reference Alonso2023; Brasselet and Alonso, Reference Brasselet and Alonso2023).) In the first section, we introduce various biophysical applications of SMOLM and labeling strategies that enable fluorophore orientations to sensitively probe the target of interest. We then discuss how light interacts with fluorescent molecules and vice versa, which establishes how microscope images can be used to sensitively measure molecular orientation. We next describe various methods for measuring SM orientations, followed by coverage of image analysis methods, including iterative methods for solving inverse problems and deep learning-based algorithms. The review concludes with an outlook suggesting future directions for SMOLM.
Sensing biomolecular architectures at the nanoscale: labeling strategies and applications
SMOLM can be applied to study a wide variety of targets, e.g., protein assemblies, nucleic acids, and lipids, and a broad variety of labeling and photochemistry have been harnessed to enable fluorophore orientations to faithfully probe the organization of biomolecules within the sample. We summarize recently reported labeling strategies in SMOLM in Figure 1 and their applications in Figures 2–4 and Table 1.

Figure 1. Representative labeling techniques in SMOLM. (a) Alexa Fluor 488-phalloidin conjugate labeling an actin filament (F-actin) (adapted from Rimoli et al., Reference Rimoli, Valades-Cruz, Curcio, Mavrakis and Brasselet2022). (b) Position and orientation of bis-((N-iodoacetyl)piperazinyl) sulfonerhodamine (BSR) on the kinesin protein structure (adapted from Sosa et al., Reference Sosa, Peterman, Moerner and Goldstein2001). (c) B-form double-stranded DNA internally labeled with covalently attached Cy3 and Cy5 dyes (adapted from Mortensen et al., Reference Mortensen, Sung, Flyvbjerg and Spudich2015). (d) Concept of molecular tension DNA probes (adapted from Brockman et al., Reference Brockman, Blanchard, Pui-Yan, Derricotte, Zhang, Fay, Lam, Evangelista, Mattheyses and Salaita2018). (e) Molecular rotors transiently bind to amyloid fibrils (adapted from Sarkar et al., Reference Sarkar, Namboodiri and Kumbhakar2023). (f) SYTOX orange dye intercalating within λ-DNA (adapted from Backer et al., Reference Backer, Lee and Moerner2016). (g) 1,1′-Dioctadecyl-3,3,3′,3′-Tetramethylindocarbocyanine Perchlorate (DiI) and merocyanine 540 (MC540) bound to gel- and fluid-like supported lipid bilayers, respectively (adapted from Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020).
Table 1. Labeling strategies for SMOLM and their applications

Emitters other than single molecules, with various labeling strategies and applications: Fluorescence from quantum rods (Lippert et al., Reference Lippert, Dadosh, Hadden, Karnawat, Diroll, Murray, Holzbaur, Schulten, Reck-Peterson and Goldman2017; Ohmachi et al., Reference Ohmachi, Komori, Iwane, Fujii, Jin and Yanagida2012), scattered light from gold nanorods (Beckwith and Yang, Reference Beckwith and Yang2021), and optically detected magnetic resonance imaging using nitrogen-vacancy centers in diamond (Backlund et al., Reference Backlund, Kehayias and Walsworth2017).
Covalent labeling of target structures
Many SMLM techniques, e.g., stochastic optical reconstruction microscopy (STORM) (Rust et al., Reference Rust, Bates and Zhuang2006) and (fluorescence) photoactivation localization microscopy [(f)PALM] (Betzig et al., Reference Betzig, Patterson, Sougrat, Lindwasser, Olenych, Bonifacino, Davidson, Lippincott-Schwartz and Hess2006; Hess et al., Reference Hess, Girirajan and Mason2006) achieve SM blinking via specific photochemical conditions, e.g., by using specific illumination intensities and/or chemical imaging buffers. The target is labeled by covalently attaching an organic fluorophore or via fusing it to a fluorescent protein (Li and Vaughan, Reference Li and Vaughan2018). Due to the high rotational mobility of many chemical linkers (Sahoo et al., Reference Sahoo, Roccatano, Hennig and Nau2007; Doose et al., Reference Doose, Neuweiler, Barsch and Sauer2007; Sindbert et al., Reference Sindbert, Kalinin, Nguyen, Kienzler, Clima, Bannwarth, Appel, Müller and Seidel2011; Chen et al., Reference Chen, Zaro and Shen2013; Beane et al., Reference Beane, Boldt, Kirkwood and Mulvaney2014; Gräwe and Stein, Reference Gräwe and Stein2021), fluorescent probes usually rotate independently of the target molecule. Therefore, the probe and its attachment to the target must be carefully designed for SMOLM measurements. Here, we introduce labeling strategies that constrain the orientation of the fluorophores in a controlled relationship to the target structure.
Organization of actin filaments via covalent conjugation to phalloidin
The structural organization of actin filaments is crucial for various cellular processes, including motility, division, and force generation, all of which are fundamental to understanding cell mechanics. Accurately interpreting the orientational dynamics of fluorescent probes when studying actin filaments depends significantly on the rigidity of the linker connecting the fluorophore to the target molecule. Importantly, the orientational dynamics of fluorescent probes are influenced by both environmental forces (e.g., solvent collisions) and forces induced by the target of interest. It has been shown that even though phalloidin binds sufficiently rigidly to actin filaments, different linkers between the fluorophore and phalloidin exhibit different rigidities (Figure 1a).
Measuring the orientations of phalloidin-conjugated fluorescent molecules under identical labeling conditions, Valades Cruz et al. show that Atto 633-phalloidin exhibits a perpendicular orientation to actin stress fibers with a small wobble angle, whereas Alexa 488-phalloidin exhibits parallel orientations to actin stress fibers with slightly greater wobble angle (Figure 2a) (Valades Cruz et al., Reference Valades Cruz, Shaban, Kress, Bertaux, Monneret, Mavrakis, Savatier and Brasselet2016). Alexa 647-phalloidin freely rotates due to its larger structure, which makes it inappropriate for studying actin fiber architectures using SMOLM. Comparing the wobbling behavior of differently charged dye molecules, including negatively charged Alexa 488, positively charged Atto 633, and neutral Atto 565, the authors surmise that the differences in wobbling of phalloidin conjugates are mostly attributed to the linker length; the linker length of Atto 565 is similar to that of Alexa 488, and they exhibit similar wobbling behavior. Similar relative degrees of rotational flexibility were also observed by (Figure 2b) Bruggeman et al. (Reference Bruggeman, Zhang, Needham, Körbel, Daly, Cheetham, Peters, Wu, Klymchenko, Davis, Paluch, Klenerman, Lew, O’Holleran and Lee2024).

Figure 2. Imaging protein assemblies using SMOLM. (a) Polar-dSTORM imaging of actin stress fibers labeled with Alexa Fluor 488, Atto 633, and Alexa Fluor 647. Colors indicate the polarization factor P, equivalent here to linear dichroism LD, superimposed on grayscale dSTORM images (adapted from Valades Cruz et al., Reference Valades Cruz, Shaban, Kress, Bertaux, Monneret, Mavrakis, Savatier and Brasselet2016). (b) Representative raw and hue-saturation-value (HSV) images of phalloidin-AF488 and phalloidin-AF647 bound to actin in fixed HeLa cells and distributions of the average degree of linear polarization (DoLP) for both fluorophores. Hue: angle of linear polarization (AoLP); saturation: DoLP; value: brightness (adapted from Bruggeman et al., Reference Bruggeman, Zhang, Needham, Körbel, Daly, Cheetham, Peters, Wu, Klymchenko, Davis, Paluch, Klenerman, Lew, O’Holleran and Lee2024). (c) 4polar-STORM imaging of actin filament organization in fixed U2OS cells with color-coded wobbling angles
![]() $ \delta $
(Alexa Fluor 488-phalloidin-labeled F-actin; adapted from Rimoli et al., Reference Rimoli, Valades-Cruz, Curcio, Mavrakis and Brasselet2022). The zoomed-in regions (1–4) show the (top) STORM and (bottom) 4polar-STORM images; lines indicate orientation, and colors represent wobble angles. (d) TAB SMOLM images of amyloid fibrils transiently labeled with LDS722, color-coded by (left) polar angle
$ \delta $
(Alexa Fluor 488-phalloidin-labeled F-actin; adapted from Rimoli et al., Reference Rimoli, Valades-Cruz, Curcio, Mavrakis and Brasselet2022). The zoomed-in regions (1–4) show the (top) STORM and (bottom) 4polar-STORM images; lines indicate orientation, and colors represent wobble angles. (d) TAB SMOLM images of amyloid fibrils transiently labeled with LDS722, color-coded by (left) polar angle
![]() $ \theta $
(rad) and (middle) wobble angle
$ \theta $
(rad) and (middle) wobble angle
![]() $ \varOmega $
(sr). The polar angle histogram reveals two distinct binding modes (adapted from Sarkar et al., Reference Sarkar, Namboodiri and Kumbhakar2023). (e) Visualization of growing and decaying amyloid-beta fibrils using (top) SMLM and (bottom) SMOLM with lines color-coded according to Nile blue orientation (adapted from Sun et al., Reference Sun, Ding, Zhou, Porter and Lew2024). (f) SMOLM images and orientation distributions for representative KFE8L, KFE8D, and Aβ42 fibrils (adapted from Zhou et al., Reference Zhou, O’Neill, Ding, Zhang, Rudra and Lew2024a). In each figure, Nile red orientations are plotted and color-coded relative to the long axis (
$ \varOmega $
(sr). The polar angle histogram reveals two distinct binding modes (adapted from Sarkar et al., Reference Sarkar, Namboodiri and Kumbhakar2023). (e) Visualization of growing and decaying amyloid-beta fibrils using (top) SMLM and (bottom) SMOLM with lines color-coded according to Nile blue orientation (adapted from Sun et al., Reference Sun, Ding, Zhou, Porter and Lew2024). (f) SMOLM images and orientation distributions for representative KFE8L, KFE8D, and Aβ42 fibrils (adapted from Zhou et al., Reference Zhou, O’Neill, Ding, Zhang, Rudra and Lew2024a). In each figure, Nile red orientations are plotted and color-coded relative to the long axis (
![]() $ {u}_x $
) of each fiber.
$ {u}_x $
) of each fiber.
Using the phalloidin-conjugated fluorophores, Rimoli et al. recently showed that SMOLM can resolve different nanoscale organizations of actin filament-based structures in mammalian cells (Figure 2c) (Rimoli et al., Reference Rimoli, Valades-Cruz, Curcio, Mavrakis and Brasselet2022); thin ventral and transverse arc stress fibers consist of highly aligned actin filaments, whereas thick peripheral and off-plane oriented dorsal stress fibers and focal adhesions consist of filaments with mixed orientations. The observations, especially within the dense assemblies, are uniquely enabled by orientation measurements using SMOLM.
Motor protein dynamics via bifunctional conjugation
Understanding the motions of motor proteins is crucial for understanding their mechanical and functional roles in cellular processes. One effective labeling strategy to study these dynamics is to attach fluorophores using more than one chemical linker to the target molecule, e.g., a bifunctional fluorophore that attaches to two separate residues of the target protein. In this way, the fluorophore’s orientation is rigidly tied to the orientation of the target. For example, bifunctional rhodamine (Corrie et al., Reference Corrie, Craik and Munasinghe1998) bound to two cysteines has been used to resolve the tilt, twist, and movement of myosin motors (Corrie et al., Reference Corrie, Brandmeier, Ferguson, Trentham, Kendrick-Jones, Hopkins, van der, Goldman, Sabido-David, Dale, Criddle and Irving1999; Forkey et al., Reference Forkey, Quinlan, Alexander Shaw, Corrie and Goldman2003; Yildiz et al., Reference Yildiz, Forkey, McKinney, Ha, Goldman and Selvin2003).
Beausang et al. show the stepping events of myosin V at sub-millisecond temporal resolution by labeling calmodulins along the lever arm with rhodamine (Beausang et al., Reference Beausang, Shroder, Nelson and Goldman2013). They observed short-lived substeps (~10 to 15 ms), marked by highly disordered lever-arm orientations, which were interpreted as random fluctuations occurring when the detached head searched for the next binding site. The increased wobble during every other step aligns with the hand-over-hand mechanism and thermal search. These findings extend our understanding of the mechanical and thermal dynamics involved in the biophysical function of myosin V.
Another fluorophore, bis-((N-iodoacetyl)piperazinyl) sulfonerhodamine (BSR) has been used to track the translation and rotation of kinesin along microtubules (Figure 1b) (Peterman et al., Reference Peterman, Sosa, Goldstein and Moerner2001; Sosa et al., Reference Sosa, Peterman, Moerner and Goldstein2001; Asenjo et al., Reference Asenjo, Krohn and Sosa2003). Attaching BSR to specific cysteine residues on kinesin enables precise monitoring of its orientation relative to the microtubule. SMOLM measurements revealed that, in the presence of AMP-PNP (a nonhydrolyzable analog of ATP), the kinesin motor domain maintains a rigid orientation with respect to the microtubule. Interestingly, in the presence of ADP, the motor domain transitions to a highly mobile state, which may be crucial for the 8-nm stepping motion of kinesin during processive movement (Sosa et al., Reference Sosa, Peterman, Moerner and Goldstein2001). A later study showed that these measured orientations align well with a hand-over-hand movement mechanism (Asenjo et al., Reference Asenjo, Krohn and Sosa2003).
Other multifunctional linkers, e.g., fluorescein arsenical hairpin (FlAsH) (Griffin et al., Reference Griffin, Adams and and Tsien1998) and ReAsH (Adams et al., Reference Adams, Gross, Martin, Walkup, Yao, Llopis and Tsien2002), its resorufin-based cousin, that bind to four cysteines of a target protein, may also be used in SMOLM. Both FlAsH and ReAsH only become fluorescent upon proper binding and orientation of the tetracysteine motif (Walker et al., Reference Walker, Rablen and Schepartz2016). The drawback of these multifunctional strategies is that the labeling yield is generally low, and improperly labeled species, e.g., with only a single functional attachment, must be carefully removed to avoid artifacts (Peterman et al., Reference Peterman, Sosa, Goldstein and Moerner2001).
DNA structure, dynamics, and tension sensing via covalent conjugation
Recent advancements have also showcased SMOLM’s utility for elucidating the structure and dynamics of engineered DNA structures (Cho et al., Reference Cho, Park, Huh, Gopinath and Lee2023; Zhan et al., Reference Zhan, Peil, Jiang, Wang, Mousavi, Xiong, Shen, Shang, Ding, Lin, Ke and Liu2023). A study using short double-stranded DNA molecules internally labeled with two distinct fluorophores (Cy3 and Cy5, Figure 1c) by Mortensen et al. demonstrated the ability to resolve fluorophore separations as small as 10 base pairs, while accurately determining the 3D orientation of DNA molecules. Their findings establish the use of short, double-labeled DNA molecules as probes for mapping the 3D orientation of any structure to which they can be firmly attached (Mortensen et al., Reference Mortensen, Sung, Flyvbjerg and Spudich2015, Reference Mortensen, Sung, Spudich and Flyvbjerg2016).
Similarly, Hübner et al. utilized 2D rectangular DNA origami to study the binding orientations of ATTO 647N, ATTO 643, and Cy5 in different nanoenvironments (Figure 3a) (Hübner et al., Reference Hübner, Joshi, Aksimentiev, Stefani, Tinnefeld and Acuna2021). They found that the nanoenvironment is crucial in determining the orientation of fluorophores. For instance, creating additional space by omitting nucleotides adjacent to a double-stranded region leads to stronger binding and a narrower, more defined distribution of dye orientations. Additionally, the dynamics of dye molecules around a DNA helix is affected by electrostatic and hydrophobic interactions, which complicates the accurate prediction of their final orientation within a DNA origami structure.

Figure 3. Imaging nucleic-acid structures and flexibility using SMOLM. (a) DNA helical winding of a scaffold strand (gray) and ssDNA staple (red line) labeled with a fluorophore (red dot), and orientation distributions of ATTO 647N and ATTO 643 within DNA origami structures 1 and 2 (adapted from Hübner et al., Reference Hübner, Joshi, Aksimentiev, Stefani, Tinnefeld and Acuna2021). (b) (top) AFM and (bottom) three SMOLM views of Cy5 orientations within 4-arm Holliday Junction complexes (HJs) with interduplex angles of 60°, 90°, and 120° (adapted from Cervantes-Salguero et al., Reference Cervantes-Salguero, Kadrmas, Ward, Lysne, Wolf, Piantanida, Pascual and Knowlton2024). Mean orientations of populations and subpopulations are denoted by red and blue arrows, respectively. (c) Controlled orientations of doubly linked Cy3 and Cy5 molecules within DNA origami structures featuring different numbers of missing base pairs (adapted from Adamczyk et al., Reference Adamczyk, Huijben, Sison, Di Luca, Chiarelli, Vanni, Brasselet, Mortensen, Stefani, Pilo-Pais and Acuna2022). (d) (top left) Diagram and (bottom) SMOLM image of a plectoneme formed by a single supercoiled DNA molecule and distribution of SYTOX orange orientations along a typical individual strand aligned along the x-axis (adapted from Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021). Colors represent azimuthal orientations (top right) Typical orientation distribution of a supercoiled strand before it twists around itself. (e) Histograms of fluorescence polarization of DNA intercalators under stretching forces of 3, 7, and 35 pN (left to right) above the onset of the overstretching transition, along with illustrations of tilted intercalators (adapted from Backer et al., Reference Backer, Biebricher, King, Wuite, Heller and Peterman2019).
Cervantes-Salguero et al. explored the use of DNA origami to manipulate directly the orientations of cyanine dyes (Cervantes-Salguero et al., Reference Cervantes-Salguero, Biaggne, Youngsman, Ward, Kim, Li, Hall, Knowlton, Graugnard and Kuang2022) and to control the interduplex angles of dye-labeled Holliday Junction complexes (Figure 3b) (Cervantes-Salguero et al., Reference Cervantes-Salguero, Kadrmas, Ward, Lysne, Wolf, Piantanida, Pascual and Knowlton2024). They discovered that sequence-dependent partial intercalation of the dye could control its polar angle throughout a full revolution of a DNA double helix with a dispersion as small as ±4.5° within a 1.7 nm range. Additionally, they characterized experimentally the orientational constraints that Holliday Junctions impose on dye orientations; tuning the template conformation enabled the dye-template heterogeneity to be minimized.
In related work, Adamczyk et al. have demonstrated direct DNA engineering to control Cy5 and Cy3 orientations by doubly linking them to hybridized strands while leaving unpaired bases in the origami scaffold (Figure 3c) (Adamczyk et al., Reference Adamczyk, Huijben, Sison, Di Luca, Chiarelli, Vanni, Brasselet, Mortensen, Stefani, Pilo-Pais and Acuna2022). By varying the number of unpaired bases (from 0 to 8), the orientations of Cy5 and Cy3 were adjusted from perpendicular to parallel relative to the DNA double helix. With no unpaired bases, the dyes remained constrained and aligned perpendicularly. As the number of unpaired bases increased to 2, 4, or 6, the increased flexibility of the linker and additional spatial accommodation allowed the dyes greater rotational mobility when interacting with the DNA. At eight unpaired bases, the linkers fully extended, causing the fluorophores to align parallel to the DNA and become rotationally constrained.
Another promising application of SMOLM uses labeled DNA nanostructures to sense mechanical forces. Studies have shown that when Cy3B is covalently attached to the terminus of a DNA duplex, it aligns perpendicularly to the duplex’s long axis (Iqbal et al., Reference Iqbal, Arslan, Okumus, Wilson, Giraud, Norman, Ha and Lilley2008). Consequently, when attached to DNA hairpin-based tension probes, the 3D orientation of piconewton cellular receptor forces can be determined using ensemble fluorescence polarization (Figure 1d) (Brockman et al., Reference Brockman, Blanchard, Pui-Yan, Derricotte, Zhang, Fay, Lam, Evangelista, Mattheyses and Salaita2018; Blanchard et al., Reference Blanchard, Combs, Brockman, Kellner, Glazier, Su, Bender, Bazrafshan, Chen, Quach, Li, Mattheyses and Salaita2021). SMOLM has the potential to improve the sensitivity of these sensors to the single-molecule level.
Transient labeling of target structures
Binding-activated fluorescence is another mechanism to achieve SM blinking. In point accumulation for imaging in nanoscale topography (PAINT) (Sharonov and Hochstrasser, Reference Sharonov and Hochstrasser2006; Kuo and Hochstrasser, Reference Kuo and Hochstrasser2011; Tholen et al., Reference Tholen, Tas, Wang and Albertazzi2023), the fluorescence quantum yield of Nile red (NR), merocyanine 540, and other lipophilic probes increases within a non-polar chemical environment, e.g., when bound to a lipid bilayer. Since this initial demonstration, many variants of binding-activated SM blinking have been developed, including amyloid binding using amyloidophilic dyes (TAB, Spehar et al., Reference Spehar, Ding, Sun, Kedia, Lu, Nahass, Lew and Bieschke2018), DNA labeling using intercalating dyes (binding-activated localization microscopy, BALM (Schoen et al., Reference Schoen, Ries, Klotzsch, Ewers and Vogel2011), and labeling a variety of biomolecules using dye-labeled oligonucleotides (DNA-PAINT, Jungmann et al., Reference Jungmann, Steinhauer, Scheible, Kuzyk, Tinnefeld and Simmel2010, Reference Jungmann, Avendaño, Woehrstein, Dai, Shih and Yin2014; Steen et al., Reference Steen, Unterauer, Masullo, Kwon, Perovic, Jevdokimenko, Opazo, Fornasiero and Jungmann2024). Unlike STORM and (f)PALM, which are limited by photobleaching of the fluorescent probes, the PAINT family of methods can collect an infinite number of localizations, due to the nearly limitless supply of fresh labels, in principle. The precise nature of dye-target interaction determines how the orientation of a fluorophore is related to the dynamics or organization of the target sample. Here, we discuss some PAINT-based methods that have been used in SMOLM.
Amyloid aggregate structure and dynamics via transient binding of amyloidophilic dyes
A fundamental question in the study of amyloid-related neurodegenerative diseases, such as Alzheimer’s, is how the structural organization of amyloid aggregates influences their pathological behavior. SMOLM is a powerful tool to reveal these nanoscale structural characteristics, providing insights that go beyond conventional methods like atomic force microscopy (AFM) and cryo-electron microscopy (cryo-EM). For example, the amyloidophilic dyes thioflavin T (ThT) (Spehar et al., Reference Spehar, Ding, Sun, Kedia, Lu, Nahass, Lew and Bieschke2018) and thioflavin X (ThX) (Needham et al., Reference Needham, Weber, Varela, Fyfe, Do, Xu, Tutton, Cliffe, Keenlyside, Klenerman, Dobson, Hunter, Müller, O’Holleran, Bohndiek, Snaddon and Lee2020), in addition to the lipophilic dyes Nile red (Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020) and Nile blue (Sun et al., Reference Sun, Ding, Zhou, Porter and Lew2024), have been used to transiently label amyloid aggregates for SMLM and SMOLM. These dyes only emit fluorescence when they are in the vicinity of the hydrophobic fibril surface; otherwise, their fluorescence quantum yield is low. SMOLM has shown that these dyes bind in a preferential direction to the grooves formed by cross-β sheets within fibrils, i.e., parallel to the fibril backbone (Krebs et al., Reference Krebs, Bromley and Donald2005; Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020). Moreover, TAB dyes appear to exhibit a variety of orientations when bound to smaller oligomers (Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020; Ding and Lew, Reference Ding and Lew2021), suggesting that these dyes may be useful for quantifying the organization of amyloid aggregates and studying how they disrupt cell membranes (Danzer et al., Reference Danzer, Haasen, Karow, Moussaud, Habeck, Giese, Kretzschmar, Hengerer and Kostka2007; Outeiro et al., Reference Outeiro, Putcha, Tetzlaff, Spoelgen, Koker, Carvalho, Hyman and McLean2008). One significant development in TAB imaging is the use of dyes with improved signal-to-background ratios (SBR); Ding et al. reported that the background when using NR is reduced by 10-fold compared to ThT (Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020; Ding and Lew, Reference Ding and Lew2021). Further, ThX exhibits a 5-fold improvement in brightness and a 7-fold increase in binding affinity compared to ThT (Needham et al., Reference Needham, Weber, Varela, Fyfe, Do, Xu, Tutton, Cliffe, Keenlyside, Klenerman, Dobson, Hunter, Müller, O’Holleran, Bohndiek, Snaddon and Lee2020) with the potential to produce dramatically more detailed SMOLM measurements.
Amyloid fibrils, such as those formed by amyloid-beta and alpha-synuclein, and other β-sheet peptide self-assemblies have since emerged as exciting applications for SMOLM studies using these dyes. For instance, Sarkar et al. discovered that SYPRO orange and LDS722, two molecular rotor dyes, exhibit distinct orientation characteristics when bound to amyloid fibrils compared to NR (Figures 1e and 2d) (Sarkar et al., Reference Sarkar, Namboodiri and Kumbhakar2023). Besides a population oriented parallel to the fibril, they observed an additional population with an inclined orientation, indicating diverse binding modes at different sites such as the fibril core, interfibril grooves, surface edges, ditches, and confined spaces in the fibril network. This structural diversity is crucial for understanding the biophysical properties of these environments, such as variations in local polarity, viscosity, and specific interactions like hydrogen bonding or π–π stacking.
Another critical biophysical question is understanding how the underlying molecular organization influences the growth and decay of fibrillar structures. Sun et al. used Nile blue to investigate the architecture and dynamics of Aβ42 fibrils (Figure 2e) (Sun et al., Reference Sun, Ding, Zhou, Porter and Lew2024). SMOLM revealed that assemblies with ordered and uniformly oriented structures are indicative of stable Aβ42 fibrils. Further, fibrils that show increasing uniformity are typically in a state of growth, whereas those that become more disordered correspond to decaying structures. SMOLM also revealed that locally disordered regions can facilitate large-scale fibrillar remodeling.
In another study, Zhou et al. used NR to reveal the helical (bilayer) ribbon architecture of fibrils of the engineered peptide KFE8 and recombinant Aβ42. Precise SMOLM measurements quantified the tilt of both the inner and outer layers of the fibrils relative to the long axis (Figure 2f) (Zhou et al., Reference Zhou, O’Neill, Ding, Zhang, Rudra and Lew2024a). Moreover, SM orientations revealed that the architectures of both KFE8 and Aβ42 are consistent with a helical bilayer ribbon, rather than a helical monolayer. However, KFE8 exhibits larger tilt angles, resulting in a higher diameter-to-pitch ratio, which indicates a more pronounced helicity; Aβ42 resembles an approximately straight line with only a modest backbone tilt. Without orientation data, these differences are difficult to discern in SMLM. SMOLM further enabled the differentiation of polymorphic branched and curved morphologies in KFE8, revealing significantly greater backbone heterogeneity compared to the more uniform straight Aβ42 fibrils.
DNA structure and dynamics via transient binding of DNA intercalators
The fluorescence of many DNA intercalating dyes (Flors et al., Reference Flors, Ravarani and David2009) is enhanced upon binding to double-stranded DNA; imaging these dyes at the SM level enables binding-activated localization microscopy (BALM) (Schoen et al., Reference Schoen, Ries, Klotzsch, Ewers and Vogel2011). It has been shown that SYTOX orange binds perpendicularly to the axis of λ-DNA (Figure 1f) (Backer et al., Reference Backer, Lee and Moerner2016), and YOYO-1 dyes exhibit a primary binding mode perpendicular to the DNA axis and a secondary binding mode parallel to the DNA axis (Larsson et al., Reference Larsson, Carlsson, Jonsson and Albinsson1994; Valades Cruz et al., Reference Valades Cruz, Shaban, Kress, Bertaux, Monneret, Mavrakis, Savatier and Brasselet2016; Mazidi et al., Reference Mazidi, King, Zhang, Nehorai and Lew2019). Therefore, they have been used to resolve tangling, bending, and supercoiling of DNA (Figure 3d) (Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021). In contrast to SYTOX orange and YOYO-1, SiR-Hoechst exhibits nonspecific binding orientations due to its flexible four-carbon linker even though Hoechst is directly attached to the DNA strand. Therefore, it is not suitable for SMOLM (Backer et al., Reference Backer, Lee and Moerner2016).
Studies have shown that the orientation of intercalators can reveal structural differences between B-DNA and mechanically extended S-DNA. Backer et al. demonstrated that when DNA is stretched beyond the overstretching transition, intercalators like YOYO-1 exhibit a significant tilt, with an angle of approximately 54° relative to the S-DNA axis, in contrast to their typical perpendicular orientation (~90°) in B-DNA (Figure 3e) (Backer et al., Reference Backer, Biebricher, King, Wuite, Heller and Peterman2019). This tilting provides the first experimental evidence of inclined base pairs in mechanically stretched DNA, offering a clearer understanding of the S-DNA conformation. However, the authors caution that the precise inclination of S-DNA base pairs might be perturbed by the presence of intercalators.
Lipid membrane structure and composition via transient binding of lipophilic dyes
The manner by which lipophilic probes transiently bind to model and cellular membranes is governed by the chemical environment and the molecular interactions within these complex assemblies. For example, the transition dipole moment of DiI (1,1′-Dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate, DiIC18(3)) bound to DPPC (1,2-Dipalmitoyl-sn-glycero-3-phosphocholine) supported lipid bilayers (SLBs) is oriented parallel to the membrane, as its hydrocarbon chains are incorporated in the nonpolar core while the chromophore headgroup resides in the polar region of the lipid bilayer. In contrast, the orientations of merocyanine 540 (MC540) are mostly perpendicular to a more fluid membrane composed of DOPC (1,2-Dioleoyl-sn-glycero-3-phosphocholine); MC540 also exhibits larger wobble angles in these membranes (Figure 1g) (Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020). Thus, the orientations of transiently bound probes measured via SMOLM reveal the chemical composition and fluidity of nanodomains within both model and cellular membranes.
The orientation spectra of NR molecules are extremely sensitive to the cholesterol concentration within the SLBs; they are confined and perpendicular to the membrane at high cholesterol concentrations and are relatively free to wobble at low cholesterol concentrations along the polar direction (parallel to the lipid acyl chains) (Figure 4a) (Ding and Lew, Reference Ding and Lew2021). This behavior aligns with the “umbrella model” of lipid bilayers, where cholesterol condenses the lipid environment and creates ordered domains that restrict molecular movement. NR-membrane interactions have also facilitated the use of spherical supported lipid bilayers as 3D calibration targets for SMOLM (Wu et al., Reference Wu, Lu and Lew2022a; Zhang et al., Reference Zhang, Guo, He, Wu, Vahey and Lew2023; Bruggeman et al., Reference Bruggeman, Zhang, Needham, Körbel, Daly, Cheetham, Peters, Wu, Klymchenko, Davis, Paluch, Klenerman, Lew, O’Holleran and Lee2024). However, its structural analog Nile blue is insensitive to cholesterol concentration within the membrane, emphasizing the importance of properly choosing probes for sensing specific membrane characteristics.

Figure 4. Imaging lipid membranes using SMOLM. (a) Distribution of polar angle (
![]() $ \theta $
) and wobble angles (
$ \theta $
) and wobble angles (
![]() $ \alpha $
along the polar direction and
$ \alpha $
along the polar direction and
![]() $ \beta $
perpendicular to the polar direction) of Nile red (NR) within DPPC bilayers with and without cholesterol (adapted from Ding and Lew, Reference Ding and Lew2021). (b) SMOLM images of NR before and after successive sphingomyelinase (SMase) treatments reveal compositional changes within the liquid-ordered (Lo) domain and minor changes in domain size and shape during the treatment (adapted from Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020). (c) Nanodomains within SLBs sensed by transiently binding NR molecules using the raPol microscope (adapted from Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022). (Left) localization density per 100 × 100 nm2 in the azimuthally polarized channel; (middle) polar angle
$ \beta $
perpendicular to the polar direction) of Nile red (NR) within DPPC bilayers with and without cholesterol (adapted from Ding and Lew, Reference Ding and Lew2021). (b) SMOLM images of NR before and after successive sphingomyelinase (SMase) treatments reveal compositional changes within the liquid-ordered (Lo) domain and minor changes in domain size and shape during the treatment (adapted from Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020). (c) Nanodomains within SLBs sensed by transiently binding NR molecules using the raPol microscope (adapted from Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022). (Left) localization density per 100 × 100 nm2 in the azimuthally polarized channel; (middle) polar angle
![]() $ \theta $
(deg); (right) wobble angle
$ \theta $
(deg); (right) wobble angle
![]() $ \Omega $
(sr). (d) Orientations of Nile red (NR) transiently bound to spherical supported lipid bilayers (SLBs) after a 7-day incubation (left) without and (right) with Aβ42 monomers (adapted from Zhang et al., Reference Zhang, Guo, He, Wu, Vahey and Lew2023). Localizations are color-coded by (top) polar angle
$ \Omega $
(sr). (d) Orientations of Nile red (NR) transiently bound to spherical supported lipid bilayers (SLBs) after a 7-day incubation (left) without and (right) with Aβ42 monomers (adapted from Zhang et al., Reference Zhang, Guo, He, Wu, Vahey and Lew2023). Localizations are color-coded by (top) polar angle
![]() $ \theta $
(deg) and (bottom) wobble angle
$ \theta $
(deg) and (bottom) wobble angle
![]() $ \Omega $
(sr). All images are lateral (xy) views unless otherwise marked. (e) SMOLM images of an HEK-293T cell. Localizations are (left) color-coded by and (right) oriented along azimuthal angle
$ \Omega $
(sr). All images are lateral (xy) views unless otherwise marked. (e) SMOLM images of an HEK-293T cell. Localizations are (left) color-coded by and (right) oriented along azimuthal angle
![]() $ \phi $
(deg). (Right) Zoomed image of the boxed region at left, color-coded by wobble angle
$ \phi $
(deg). (Right) Zoomed image of the boxed region at left, color-coded by wobble angle
![]() $ \Omega $
(sr). The inset histogram shows the distribution of the measured wobble angle within the regions marked by yellow and white boxes (adapted from Zhang et al., Reference Zhang, Guo, He, Wu, Vahey and Lew2023).
$ \Omega $
(sr). The inset histogram shows the distribution of the measured wobble angle within the regions marked by yellow and white boxes (adapted from Zhang et al., Reference Zhang, Guo, He, Wu, Vahey and Lew2023).
SMOLM has been used to study enzyme-induced reorganization of lipid domains. For instance, Lu et al. visualized the restructuring of lipid domains by sphingomyelinase (SMase), an enzyme that catalyzes the hydrolysis of sphingomyelin into ceramide by measuring the orientation spectra of NR and MC540 (Figure 4b) (Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020). Upon the addition of SMase, membrane composition shifted as ceramide formed and reorganized the structure. A dose-dependent disappearance of cholesterol-rich liquid-ordered domains was observed, and these regions were replaced by ceramide-rich domains.
Zhang et al. recently reported simultaneous ordering and damage of a lipid bilayer caused by cholesterol-loaded methyl-β-cyclodextrin via tracking the orientations and positions of single NR molecules transiently bound to DPPC SLBs (Figure 4c) (Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022). The study revealed that while cholesterol deposition reduces NR’s rotational diffusion, MβCD-chol somewhat counter-intuitively increases translational motions within the membrane as it nonuniformly dissolves the SLB. Therefore, SMOLM’s ability to measure rotations and positions simultaneously yields insights into complex changes in membrane structure that cannot be quantified via traditional single-particle tracking or polarization anisotropy alone.
SMOLM with NR has also been applied to study complex membrane-amyloid interactions with single-molecule sensitivity. Zhang et al. demonstrated that when amyloid aggregates infiltrate lipid membranes, they significantly change the rotational dynamics of NR molecules. Specifically, NR exhibited increased wobble angles in regions infiltrated by amyloid aggregates compared to those in pure DPPC SLBs. Further, the study found that Aβ42 aggregates interacting with lipid membranes tend to form smaller assemblies, such as oligomers and protofibrils, rather than fully developed fibrils (Figure 4d).
Such dye-membrane interactions are not limited to model systems. For example, SMOLM has revealed diverse binding modes of MC540 on cell membranes, influenced by several factors including membrane tension, fluidity, and potential (Zhang et al., Reference Zhang, Guo, He, Wu, Vahey and Lew2023). Imaging the wobble angle of MC540 reveals that the rigidity of the coverslip reduces membrane fluidity near the cell-coverslip interface, while lipids at the tip of a membrane protrusion are more fluid than those in surrounding regions (Figure 4e).
Other labeling strategies and applications
SMs embedded within polymer films can also be used to detect architectural changes and mechanical fractures since rotational motions are sometimes more sensitive to these changes compared to translational motions. Early SM orientation measurements used defocused imaging to map the orientations of dye molecules at various positions within dendrimers and below and above the glass transition temperature of the host material (Melnikov et al., Reference Melnikov, Yeow, Uji-i, Cotlet, Müllen, De Schryver, Enderlein and Hofkens2007; Dedecker et al., Reference Dedecker, Muls, Deres, Uji-i, Hotta, Sliwa, Soumillion, Müllen, Enderlein and Hofkens2009; Zheng et al., Reference Zheng, Kuang and Zhao2010; Ham et al., Reference Ham, Yang, Schlosser, Würthner and Kim2014; Paeng and Kaufman, Reference Paeng and Kaufman2016). More recently, researchers have used SMOLM to detect the nanoscale softening (Zhang et al., Reference Zhang, Lu, Ding and Lew2018) and deformation (Krause et al., Reference Krause, Neumann, Fröbe, Magerle and Von Borczyskowski2016; Wang et al., Reference Wang, Marr, Davanco, Gilman and Liddle2019) of polymer matrices as fluorophore orientations change.
Besides SMs, the orientations of luminescent and scattering nanoparticles can also be resolved by imaging systems. For example, quantum nanorods are much brighter probes compared to typical fluorescent molecules and have been used for studying the force-generating mechanism of dynein molecules (Lippert et al., Reference Lippert, Dadosh, Hadden, Karnawat, Diroll, Murray, Holzbaur, Schulten, Reck-Peterson and Goldman2017). Tracking the orientation and position of gold nanorods using scattering light has been shown to achieve sub-millisecond temporal resolution (Beckwith and Yang, Reference Beckwith and Yang2021) as the number of signal photons is no longer limited by photobleaching. However, since the size of typical quantum rods is 10 or 100 times compared to that of organic fluorophores, SMOLM is generally a less perturbative choice for studying biochemical processes. A similar concept to SMOLM has also been implemented in optically detected magnetic resonance imaging using nitrogen-vacancy centers in diamonds (Backlund et al., Reference Backlund, Kehayias and Walsworth2017).
Choosing the appropriate labeling strategy for SMOLM
The advantages and limitations of various labeling strategies, along with their applications, are summarized in Table 1. It is important to note that any exogenous probe can introduce perturbations to the biophysical structure or process under study. For instance, SYTOX orange DNA intercalators (Figure 1f), which increase quantum yield upon binding to DNA, may trap non-canonical conformations such as unstacked flanking bases upon interacting with the biomolecular surface (Biebricher et al., Reference Biebricher, Heller, Roijmans, Hoekstra, Peterman and Wuite2015; Kolbeck et al., Reference Kolbeck, Tišma, Analikwu, Vanderlinden, Dekker and Lipfert2024). Such alterations in local DNA structure can affect the conformational dynamics of the system and potentially influence the orientation data obtained through SMOLM. These perturbative effects, which may also occur with other intercalating dyes, must be carefully considered when interpreting results. Similarly, internal labeling strategies using Cy3 and Cy5 dyes (Figure 1c) can disturb local DNA conformation by replacing nucleotides within the backbone, leading to structural disorder and rapid orientational dynamics of the probe. A recent study using polarization-sensitive fluorescence microscopy has shown that Cy3 labeled single-stranded-double-stranded DNA junctions undergo significant conformational changes depending on the position and temperature (Heussman et al., Reference Heussman, Kittell, Von Hippel and Marcus2022), and Maurer et al. further demonstrated that DNA “breathing” at these junctions can shift between multiple conformational macrostates (Maurer et al., Reference Maurer, Albrecht, Herbert, Heussman, Chang, Von Hippel and Marcus2023). Fluorescent dyes can also perturb peptide aggregates; Sun et al. used the photo-oxidation of thioflavin T, a common amyloidophilic dye, to induce growth, depolymerization, and remodeling within Aβ42 fibrils (Figure 2e) (Sun et al., Reference Sun, Ding, Zhou, Porter and Lew2024). Therefore, control experiments are essential to quantify the extent of dye-induced perturbations and to ensure reliable interpretation of SMOLM data.
When selecting probe-labeling strategies for SMOLM, it is important to balance the need for site-specific information with the risk of structural disruption. Covalent labeling offers precise control over fluorophore orientation relative to the attachment site (Budiarta et al., Reference Budiarta, Streit and Beliu2024) and can provide valuable insights into the conformational dynamics of protein domains. However, rigidly attaching a fluorophore to a target protein domain with a high yield may interfere with function or may not be feasible, depending on the domain’s inherent flexibility. On the other hand, transient binding approaches mitigate these issues by avoiding high concentrations of covalently bound fluorophores; this method allows for temporary, low-concentration interactions of the dye with the target system, thereby reducing the number of labeled molecules compared to conventional labeling strategies. However, precise targeting of transiently binding probes to specific protein domains remains a challenge (Steen et al., Reference Steen, Unterauer, Masullo, Kwon, Perovic, Jevdokimenko, Opazo, Fornasiero and Jungmann2024). As is the case with SMLM, proper choice of the labeling strategy is essential for ensuring useful and robust orientation measurements with minimal perturbation in SMOLM.
Interaction between light and fluorescent molecules
In this section, we introduce how light interacts with fluorescent molecules (Valeur, Reference Valeur2002; Novotny and Hecht, Reference Novotny and Hecht2012). A photon from an optical field may be absorbed by a molecule, resulting in an electronic state transition from the singlet ground state
![]() $ {S}_0 $
, i.e., the highest occupied molecular orbital, to various vibrational levels of the singlet excited state
$ {S}_0 $
, i.e., the highest occupied molecular orbital, to various vibrational levels of the singlet excited state
![]() $ {S}_1 $
, i.e., the lowest unoccupied molecular orbital. After a fast vibrational relaxation (typically on the order of a few picoseconds), the molecule decays to the lowest energy level of
$ {S}_1 $
, i.e., the lowest unoccupied molecular orbital. After a fast vibrational relaxation (typically on the order of a few picoseconds), the molecule decays to the lowest energy level of
![]() $ {S}_1 $
. After a few nanoseconds, i.e., the fluorescence or excited-state lifetime, the molecule returns to a vibrationally excited state of
$ {S}_1 $
. After a few nanoseconds, i.e., the fluorescence or excited-state lifetime, the molecule returns to a vibrationally excited state of
![]() $ {S}_0 $
by emitting a red-shifted fluorescence photon with lower energy. The molecule may also lose its energy via nonradiative relaxation such as vibration and collision and return to the ground state, which reduces the number of photons emitted. Therefore, the quality of a molecule as a fluorophore is measured by its quantum yield (Valeur, Reference Valeur2002)
$ {S}_0 $
by emitting a red-shifted fluorescence photon with lower energy. The molecule may also lose its energy via nonradiative relaxation such as vibration and collision and return to the ground state, which reduces the number of photons emitted. Therefore, the quality of a molecule as a fluorophore is measured by its quantum yield (Valeur, Reference Valeur2002)
where
![]() $ {\gamma}_{\mathrm{r}} $
is the fluorescence rate and
$ {\gamma}_{\mathrm{r}} $
is the fluorescence rate and
![]() $ {\gamma}_{\mathrm{nr}} $
is the nonradiative relaxation rate; molecules with a quantum yield above 10% are usually considered quite fluorescent. Some widely-used fluorophores in single-molecule imaging, e.g., NR (Kucherak et al., Reference Kucherak, Oncul, Darwich, Yushchenko, Arntz, Didier, Mély and Klymchenko2010) and Rhodamine 6G (Fischer and Georges, Reference Fischer and Georges1996), may exhibit a quantum yield of >90% depending on the local environment (Li and Vaughan, Reference Li and Vaughan2018; Jradi and Lavis, Reference Jradi and Lavis2019).
$ {\gamma}_{\mathrm{nr}} $
is the nonradiative relaxation rate; molecules with a quantum yield above 10% are usually considered quite fluorescent. Some widely-used fluorophores in single-molecule imaging, e.g., NR (Kucherak et al., Reference Kucherak, Oncul, Darwich, Yushchenko, Arntz, Didier, Mély and Klymchenko2010) and Rhodamine 6G (Fischer and Georges, Reference Fischer and Georges1996), may exhibit a quantum yield of >90% depending on the local environment (Li and Vaughan, Reference Li and Vaughan2018; Jradi and Lavis, Reference Jradi and Lavis2019).
When a molecule is in the excited state
![]() $ {S}_1 $
, it may also undergo intersystem crossing due to spin-orbital coupling and enter a long-lived (microseconds to seconds) and reactive triplet state
$ {S}_1 $
, it may also undergo intersystem crossing due to spin-orbital coupling and enter a long-lived (microseconds to seconds) and reactive triplet state
![]() $ {T}_1 $
. Upon entering this state, the molecule cannot undergo repeated absorption and emission cycles; it appears to go dark. From the triplet state
$ {T}_1 $
. Upon entering this state, the molecule cannot undergo repeated absorption and emission cycles; it appears to go dark. From the triplet state
![]() $ {T}_1 $
, the molecule may return to
$ {T}_1 $
, the molecule may return to
![]() $ {S}_0 $
via phosphorescence or nonradiative relaxation. It may also undergo chemical reactions with singlet oxygen and other reactive oxygen species and permanently lose its ability to fluoresce. This process is termed photobleaching, which fundamentally limits the number of photons emitted by a fluorescent molecule and is determined by the intrinsic photophysics and photochemistry of the fluorophore (Cordes et al., Reference Cordes, Maiser, Steinhauer, Schermelleh and Tinnefeld2011; Ha and Tinnefeld, Reference Ha and Tinnefeld2012; Gust et al., Reference Gust, Zander, Gietl, Holzmeister, Schulz, Lalkens, Tinnefeld and Grohmann2014). The total number of photons emitted by an SM may be increased by decreasing the photobleaching rate via quenching the triplet state, e.g., using photostabilizers, reducing or oxidizing agents, and oxygen-scavenging systems (Rasnik et al., Reference Rasnik, McKinney and Ha2006; Aitken et al., Reference Aitken, Marshall and Puglisi2008; Vogelsang et al., Reference Vogelsang, Kasper, Steinhauer, Person, Heilemann, Sauer and Tinnefeld2008; Dave et al., Reference Dave, Terry, Munro and Blanchard2009; Hoffman et al., 2011; Lee et al., Reference Lee, Vérolet and Fürstenberg2013; Nahidiazar et al., Reference Nahidiazar, Agronskaia, Broertjes, van den Broek and Jalink2016; Glembockyte et al., Reference Glembockyte, Lin and Cosa2016; Sauer and Heilemann, Reference Sauer and Heilemann2017), or enhancing the emission rate using plasmonic nanoantennas (Kinkhabwala et al., Reference Kinkhabwala, Yu, Fan, Avlasevich, Müllen and Moerner2009; Wientjes et al., Reference Wientjes, Renger, Cogdell and van Hulst2016; Kaminska et al., Reference Kaminska, Vietz, Cuartero-González, Tinnefeld, Fernández-Domínguez and Acuna2018; Grabenhorst et al., Reference Grabenhorst, Trofymchuk, Steiner, Glembockyte and Tinnefeld2020). However, one must note that these methods could potentially perturb the imaging targets themselves (Tosheva et al., Reference Tosheva, Yuan, Matos Pereira, Culley and Henriques2020). In addition, nearby plasmonic nanoparticles will also distort the image of each fluorophore (Lim et al., Reference Lim, Ropp, Barik, Fourkas, Shapiro and Waks2016; Raab et al., Reference Raab, Vietz, Stefani, Acuna and Tinnefeld2017; Goldwyn et al., Reference Goldwyn, Smith, Busche and Masiello2018; Zuo et al., Reference Zuo, Goldwyn, Isaacoff, Masiello and Biteen2019; Bloksma and Zijlstra Reference Bloksma and Zijlstra2021; Zuo et al., Reference Zuo, Goldwyn, Masiello and Biteen2021; Moon et al., Reference Moon, Son, Yoo, Lee, Lee, Im and Kim2023; Huijben et al., Reference Huijben, Mahajan, Fahim, Zijlstra, Marie and Mortensen2024), compared to typical dipolar emission.
$ {S}_0 $
via phosphorescence or nonradiative relaxation. It may also undergo chemical reactions with singlet oxygen and other reactive oxygen species and permanently lose its ability to fluoresce. This process is termed photobleaching, which fundamentally limits the number of photons emitted by a fluorescent molecule and is determined by the intrinsic photophysics and photochemistry of the fluorophore (Cordes et al., Reference Cordes, Maiser, Steinhauer, Schermelleh and Tinnefeld2011; Ha and Tinnefeld, Reference Ha and Tinnefeld2012; Gust et al., Reference Gust, Zander, Gietl, Holzmeister, Schulz, Lalkens, Tinnefeld and Grohmann2014). The total number of photons emitted by an SM may be increased by decreasing the photobleaching rate via quenching the triplet state, e.g., using photostabilizers, reducing or oxidizing agents, and oxygen-scavenging systems (Rasnik et al., Reference Rasnik, McKinney and Ha2006; Aitken et al., Reference Aitken, Marshall and Puglisi2008; Vogelsang et al., Reference Vogelsang, Kasper, Steinhauer, Person, Heilemann, Sauer and Tinnefeld2008; Dave et al., Reference Dave, Terry, Munro and Blanchard2009; Hoffman et al., 2011; Lee et al., Reference Lee, Vérolet and Fürstenberg2013; Nahidiazar et al., Reference Nahidiazar, Agronskaia, Broertjes, van den Broek and Jalink2016; Glembockyte et al., Reference Glembockyte, Lin and Cosa2016; Sauer and Heilemann, Reference Sauer and Heilemann2017), or enhancing the emission rate using plasmonic nanoantennas (Kinkhabwala et al., Reference Kinkhabwala, Yu, Fan, Avlasevich, Müllen and Moerner2009; Wientjes et al., Reference Wientjes, Renger, Cogdell and van Hulst2016; Kaminska et al., Reference Kaminska, Vietz, Cuartero-González, Tinnefeld, Fernández-Domínguez and Acuna2018; Grabenhorst et al., Reference Grabenhorst, Trofymchuk, Steiner, Glembockyte and Tinnefeld2020). However, one must note that these methods could potentially perturb the imaging targets themselves (Tosheva et al., Reference Tosheva, Yuan, Matos Pereira, Culley and Henriques2020). In addition, nearby plasmonic nanoparticles will also distort the image of each fluorophore (Lim et al., Reference Lim, Ropp, Barik, Fourkas, Shapiro and Waks2016; Raab et al., Reference Raab, Vietz, Stefani, Acuna and Tinnefeld2017; Goldwyn et al., Reference Goldwyn, Smith, Busche and Masiello2018; Zuo et al., Reference Zuo, Goldwyn, Isaacoff, Masiello and Biteen2019; Bloksma and Zijlstra Reference Bloksma and Zijlstra2021; Zuo et al., Reference Zuo, Goldwyn, Masiello and Biteen2021; Moon et al., Reference Moon, Son, Yoo, Lee, Lee, Im and Kim2023; Huijben et al., Reference Huijben, Mahajan, Fahim, Zijlstra, Marie and Mortensen2024), compared to typical dipolar emission.
The orientation of fluorescent molecules relative to the applied optical field affects how they interact. Briefly, we may describe the interaction between a charge-neutral nanoparticle with an optical field by writing the multipolar interaction Hamiltonian (Novotny and Hecht, Reference Novotny and Hecht2012)
where vectors
![]() $ {\boldsymbol{p}}_e $
and
$ {\boldsymbol{p}}_e $
and
![]() $ {\boldsymbol{p}}_m $
represent the total electric and magnetic dipole moments, respectively, the matrix
$ {\boldsymbol{p}}_m $
represent the total electric and magnetic dipole moments, respectively, the matrix
![]() $ \boldsymbol{Q} $
represents the electric quadrupole moment,
$ \boldsymbol{Q} $
represents the electric quadrupole moment,
![]() $ \boldsymbol{E} $
and
$ \boldsymbol{E} $
and
![]() $ \boldsymbol{B} $
represent the electric and magnetic fields, respectively, and
$ \boldsymbol{B} $
represent the electric and magnetic fields, respectively, and
![]() $ {\boldsymbol{p}}_e\cdotp \boldsymbol{E}={\boldsymbol{p}}_e^{\top}\boldsymbol{E} $
represents the dot or inner product between vectors
$ {\boldsymbol{p}}_e\cdotp \boldsymbol{E}={\boldsymbol{p}}_e^{\top}\boldsymbol{E} $
represents the dot or inner product between vectors
![]() $ {\boldsymbol{p}}_e $
and
$ {\boldsymbol{p}}_e $
and
![]() $ \boldsymbol{E} $
. For typical SM imaging experiments where both illumination and emission are manipulated in the far-field, the magnetic dipole and electric quadrupole interactions are orders of magnitude weaker compared to the electric dipole interaction. Therefore, we describe the photon absorption and emission processes using only the electric dipole moments.
$ \boldsymbol{E} $
. For typical SM imaging experiments where both illumination and emission are manipulated in the far-field, the magnetic dipole and electric quadrupole interactions are orders of magnitude weaker compared to the electric dipole interaction. Therefore, we describe the photon absorption and emission processes using only the electric dipole moments.
The transition dipole moment is the electric dipole moment associated with the transition between two quantum states. The absorption dipole moment describes the transition between initial state
![]() $ {S}_0 $
and final state
$ {S}_0 $
and final state
![]() $ {S}_1 $
; the emission dipole moment describes the transition between initial state
$ {S}_1 $
; the emission dipole moment describes the transition between initial state
![]() $ {S}_1 $
and final state
$ {S}_1 $
and final state
![]() $ {S}_0 $
. Here, we omit the amplitude and only describe the orientation of a transition dipole using a unit vector (Figure 5a)
$ {S}_0 $
. Here, we omit the amplitude and only describe the orientation of a transition dipole using a unit vector (Figure 5a)
where
![]() $ z $
represents the direction of the optical axis. Note that due to the two-fold degeneracy of a dipole moment, this unit vector is defined over a unit hemisphere. We only consider linear dipoles here; chirality may be modeled as a coherent superposition of multiple linear dipoles with spatial phase differences (Cyphersmith et al., Reference Cyphersmith, Maksov, Hassey-Paradise, McCarthy and Barnes2011). Fundamentally, the orientation of the transition dipole moment
$ z $
represents the direction of the optical axis. Note that due to the two-fold degeneracy of a dipole moment, this unit vector is defined over a unit hemisphere. We only consider linear dipoles here; chirality may be modeled as a coherent superposition of multiple linear dipoles with spatial phase differences (Cyphersmith et al., Reference Cyphersmith, Maksov, Hassey-Paradise, McCarthy and Barnes2011). Fundamentally, the orientation of the transition dipole moment
![]() $ \boldsymbol{\mu} $
determines how the molecule interacts with the polarization of the optical field.
$ \boldsymbol{\mu} $
determines how the molecule interacts with the polarization of the optical field.

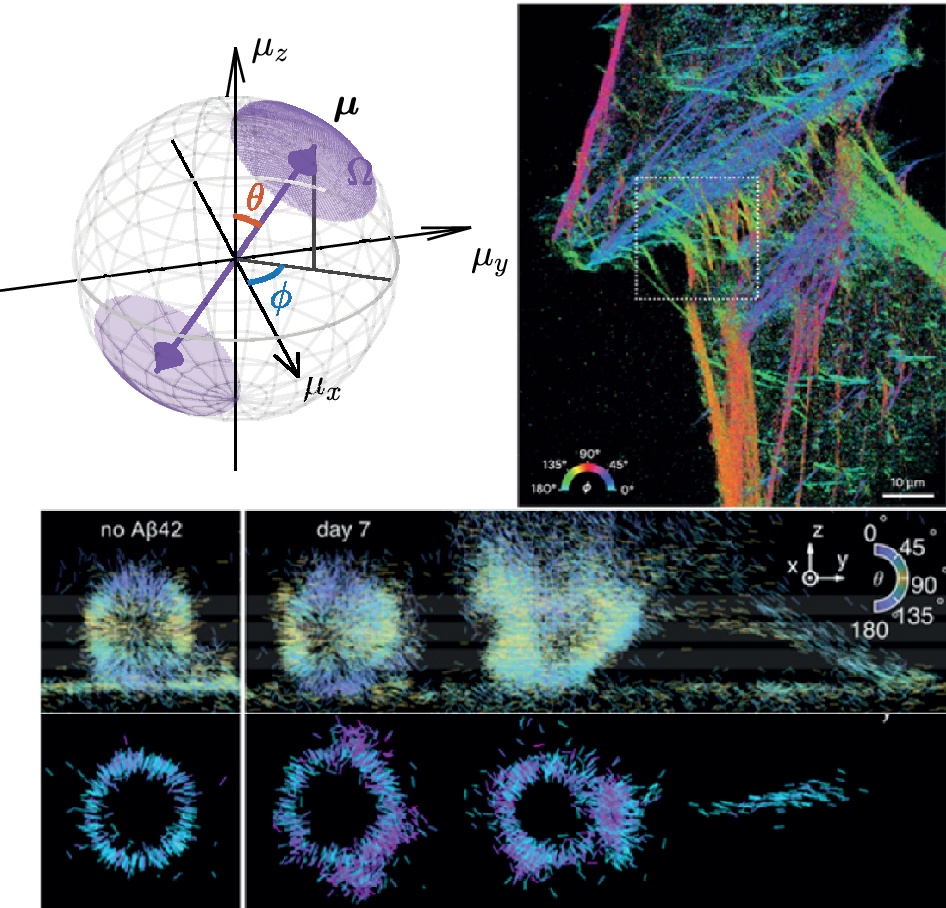
Figure 5. (a) Molecular orientation represented by a unit vector
![]() $ \boldsymbol{\mu} ={\left[{\mu}_x,{\mu}_y,{\mu}_z\right]}^{\top }={\left[\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta \right]}^{\top } $
. The wobble is modeled as a hard-edged cone with cone solid angle
$ \boldsymbol{\mu} ={\left[{\mu}_x,{\mu}_y,{\mu}_z\right]}^{\top }={\left[\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta \right]}^{\top } $
. The wobble is modeled as a hard-edged cone with cone solid angle
![]() $ \Omega $
. (b) Excitation light in typical SMOLM. A Kohler lens (KL) is used to produce a collimated illumination beam above the objective lens (OL). The absorption probability is a function of the angle between the absorption dipole moment
$ \Omega $
. (b) Excitation light in typical SMOLM. A Kohler lens (KL) is used to produce a collimated illumination beam above the objective lens (OL). The absorption probability is a function of the angle between the absorption dipole moment
![]() $ {\boldsymbol{\mu}}_{\mathrm{abs}} $
and the excitation optical field
$ {\boldsymbol{\mu}}_{\mathrm{abs}} $
and the excitation optical field
![]() $ {\boldsymbol{E}}_{\mathrm{ex}} $
(green arrows). The absorption probability is maximized if
$ {\boldsymbol{E}}_{\mathrm{ex}} $
(green arrows). The absorption probability is maximized if
![]() $ {\boldsymbol{\mu}}_{\mathrm{abs}} $
is parallel to
$ {\boldsymbol{\mu}}_{\mathrm{abs}} $
is parallel to
![]() $ {\boldsymbol{E}}_{\mathrm{ex}} $
. Colorbar: normalized absorption probability. (c) Depolarization, i.e., a non-zero angle between
$ {\boldsymbol{E}}_{\mathrm{ex}} $
. Colorbar: normalized absorption probability. (c) Depolarization, i.e., a non-zero angle between
![]() $ {\boldsymbol{\mu}}_{\mathrm{abs}} $
and
$ {\boldsymbol{\mu}}_{\mathrm{abs}} $
and
![]() $ {\boldsymbol{\mu}}_{\mathrm{em}} $
caused by rotation during the fluorescence lifetime between the absorption and emission events. (d) Depolarization caused by energy transfer between chromophores of a YOYO-1. (e,f) Anisotropic rotational diffusion models for SMs. (e) Cone half angles
$ {\boldsymbol{\mu}}_{\mathrm{em}} $
caused by rotation during the fluorescence lifetime between the absorption and emission events. (d) Depolarization caused by energy transfer between chromophores of a YOYO-1. (e,f) Anisotropic rotational diffusion models for SMs. (e) Cone half angles
![]() $ \alpha $
and
$ \alpha $
and
![]() $ \beta $
represent the area within which the molecule can wobble, and (f)
$ \beta $
represent the area within which the molecule can wobble, and (f)
![]() $ \psi $
describes the preferred direction of the wobble.
$ \psi $
describes the preferred direction of the wobble.
Absorption dipole moments
We now briefly introduce a model for light absorption by an SM. The transition dipole moment can be described as a quantum mechanical state transition, given by
where
![]() $ q $
represents the charge and
$ q $
represents the charge and
![]() $ \boldsymbol{r} $
represents its position. Kets
$ \boldsymbol{r} $
represents its position. Kets
![]() $ \left|{\psi}_0\right\rangle $
and
$ \left|{\psi}_0\right\rangle $
and
![]() $ \left|{\psi}_1\right\rangle $
represent the states associated with ground state
$ \left|{\psi}_1\right\rangle $
represent the states associated with ground state
![]() $ {S}_0 $
and excited state
$ {S}_0 $
and excited state
![]() $ {S}_1 $
, respectively. According to Fermi’s golden rule (Shankar, Reference Shankar2012), the SM’s rate of transition from
$ {S}_1 $
, respectively. According to Fermi’s golden rule (Shankar, Reference Shankar2012), the SM’s rate of transition from
![]() $ {S}_0 $
to
$ {S}_0 $
to
![]() $ {S}_1 $
in the presence of excitation field
$ {S}_1 $
in the presence of excitation field
![]() $ {\boldsymbol{E}}_{\mathrm{ex}}={\left[{E}_x,{E}_y,{E}_z\right]}^{\top } $
is given by (Figure 5b)
$ {\boldsymbol{E}}_{\mathrm{ex}}={\left[{E}_x,{E}_y,{E}_z\right]}^{\top } $
is given by (Figure 5b)
A molecule at its ground state
![]() $ {S}_0 $
is more likely to absorb an incident photon if the polarization of the photon is parallel to the absorption dipole moment
$ {S}_0 $
is more likely to absorb an incident photon if the polarization of the photon is parallel to the absorption dipole moment
![]() $ {\boldsymbol{\mu}}_{\mathrm{abs}} $
. In contrast, the absorption probability is zero if the absorption dipole moment is perpendicular to the polarization of the local electric field
$ {\boldsymbol{\mu}}_{\mathrm{abs}} $
. In contrast, the absorption probability is zero if the absorption dipole moment is perpendicular to the polarization of the local electric field
![]() $ {\boldsymbol{E}}_{\mathrm{ex}} $
.
$ {\boldsymbol{E}}_{\mathrm{ex}} $
.
Emission dipole moments
Suppose a molecule with an emission dipole moment of
![]() $ {\boldsymbol{\mu}}_{\mathrm{em}} $
located at
$ {\boldsymbol{\mu}}_{\mathrm{em}} $
located at
![]() $ \boldsymbol{r}={\left[0,0,0\right]}^{\top } $
relaxes from excited state
$ \boldsymbol{r}={\left[0,0,0\right]}^{\top } $
relaxes from excited state
![]() $ {S}_1 $
to ground state
$ {S}_1 $
to ground state
![]() $ {S}_0 $
and emits a photon. The classical far-field emission at position
$ {S}_0 $
and emits a photon. The classical far-field emission at position
![]() $ {\boldsymbol{r}}_{\mathrm{ff}} $
can be found by solving the electromagnetic wave equation for an oscillating dipole source (Novotny and Hecht, Reference Novotny and Hecht2012), yielding (Figure 6a)
$ {\boldsymbol{r}}_{\mathrm{ff}} $
can be found by solving the electromagnetic wave equation for an oscillating dipole source (Novotny and Hecht, Reference Novotny and Hecht2012), yielding (Figure 6a)
where the unit vector
represents the viewing direction,
![]() $ {c}_{\mathrm{ff}} $
is a normalization factor,
$ {c}_{\mathrm{ff}} $
is a normalization factor,
![]() $ \unicode{x1D540} $
represents the identity matrix, and
$ \unicode{x1D540} $
represents the identity matrix, and
![]() $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top } $
represents the outer product of
$ {\hat{\boldsymbol{r}}}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top } $
represents the outer product of
![]() $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $
with itself. Therefore,
$ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $
with itself. Therefore,

Figure 6. Schematic diagram of dipole emitters (a) within a medium of matched RI and (b) near the RI interface between the sample (
![]() $ {n}_2 $
) and lens immersion medium (
$ {n}_2 $
) and lens immersion medium (
![]() $ {n}_1 $
). The objective lens captures a pseudo-spherical wave (
$ {n}_1 $
). The objective lens captures a pseudo-spherical wave (
![]() $ {\boldsymbol{E}}_{\mathrm{ff}} $
and
$ {\boldsymbol{E}}_{\mathrm{ff}} $
and
![]() $ {\boldsymbol{E}}_{\mathrm{ff},3} $
) and converts it to a pseudo-plane wave (
$ {\boldsymbol{E}}_{\mathrm{ff},3} $
) and converts it to a pseudo-plane wave (
![]() $ {\boldsymbol{E}}_{\mathrm{BFP}} $
). Useful unit vectors, angles, and lengths for the derivation in this section are labeled in the figure. (c) Positions of a dipole emitter relative to the RI interface (
$ {\boldsymbol{E}}_{\mathrm{BFP}} $
). Useful unit vectors, angles, and lengths for the derivation in this section are labeled in the figure. (c) Positions of a dipole emitter relative to the RI interface (
![]() $ {z}_{\mathrm{SM}} $
) and the nominal focal plane (
$ {z}_{\mathrm{SM}} $
) and the nominal focal plane (
![]() $ {z}_f $
). (d-f) Representative intensity distributions at the BFP for SMs with orientations of (i)
$ {z}_f $
). (d-f) Representative intensity distributions at the BFP for SMs with orientations of (i)
![]() $ \theta ={0}^{\circ } $
, (ii)
$ \theta ={0}^{\circ } $
, (ii)
![]() $ \left[\theta, \phi \right]=\left[{45}^{\circ },{90}^{\circ}\right] $
, and (iii)
$ \left[\theta, \phi \right]=\left[{45}^{\circ },{90}^{\circ}\right] $
, and (iii)
![]() $ \left[\theta, \phi \right]=\left[{90}^{\circ },{90}^{\circ}\right] $
when (d) the sample RI matches that of the lens immersion medium (1.515) and when the sample RI is (e)
$ \left[\theta, \phi \right]=\left[{90}^{\circ },{90}^{\circ}\right] $
when (d) the sample RI matches that of the lens immersion medium (1.515) and when the sample RI is (e)
![]() $ {n}_2=1.33 $
and (f)
$ {n}_2=1.33 $
and (f)
![]() $ {n}_2=1 $
. The numerical aperture is
$ {n}_2=1 $
. The numerical aperture is
![]() $ \mathrm{NA}=1.4 $
. Colorbar: normalized intensity.
$ \mathrm{NA}=1.4 $
. Colorbar: normalized intensity.
i.e., the fluorescence intensity has a sine-square dependence on the angle between the molecular orientation
![]() $ {\boldsymbol{\mu}}_{\mathrm{em}} $
and viewing direction
$ {\boldsymbol{\mu}}_{\mathrm{em}} $
and viewing direction
![]() $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $
. In addition, optical field is always perpendicular to the propagation direction, i.e.,
$ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $
. In addition, optical field is always perpendicular to the propagation direction, i.e.,
Note that even though both the absorption and emission dipole moments can be used for measuring the orientation of fluorescent molecules, they are not necessarily parallel to each other. Depolarization between the absorption and emission dipoles can be quantified by measuring fluorescence anisotropy (see next section for detailed discussion). The relationship between the fluorescence lifetime and rotational correlation time determines how far the molecule may rotate between an absorption and an emission event. A molecule’s emission dipole moment
![]() $ {\boldsymbol{\mu}}_{\mathrm{em}} $
is decoupled from its absorption dipole moment
$ {\boldsymbol{\mu}}_{\mathrm{em}} $
is decoupled from its absorption dipole moment
![]() $ {\boldsymbol{\mu}}_{\mathrm{abs}} $
when the molecule’s rotation is much faster compared to its fluorescence lifetime (Lew et al., Reference Lew, Backlund and Moerner2013; Backlund et al., Reference Backlund, Lew, Backer, Sahl and Moerner2014; Stallinga, Reference Stallinga2015), which is typical for SMs in liquids. The correlation between
$ {\boldsymbol{\mu}}_{\mathrm{abs}} $
when the molecule’s rotation is much faster compared to its fluorescence lifetime (Lew et al., Reference Lew, Backlund and Moerner2013; Backlund et al., Reference Backlund, Lew, Backer, Sahl and Moerner2014; Stallinga, Reference Stallinga2015), which is typical for SMs in liquids. The correlation between
![]() $ {\boldsymbol{\mu}}_{\mathrm{em}} $
and
$ {\boldsymbol{\mu}}_{\mathrm{em}} $
and
![]() $ {\boldsymbol{\mu}}_{\mathrm{abs}} $
becomes prominent when the rotational correlation time is comparable to the lifetime, e.g, when molecules are embedded within dense lipid membranes (Halder et al., Reference Halder, Saha, Maity, Kumar, Sinha and Karmakar2018). Even for molecules that are immobilized within rigid substrates like polymer matrices, it is reported that these two vectors may exhibit an inclination angle of more than 20° from each other (Karedla et al., Reference Karedla, Stein, Hähnel, Gregor, Chizhik and Enderlein2015) due to the interactions between molecular orbitals and the chemical environment, and the possibility of relaxation into energy states other than
$ {\boldsymbol{\mu}}_{\mathrm{abs}} $
becomes prominent when the rotational correlation time is comparable to the lifetime, e.g, when molecules are embedded within dense lipid membranes (Halder et al., Reference Halder, Saha, Maity, Kumar, Sinha and Karmakar2018). Even for molecules that are immobilized within rigid substrates like polymer matrices, it is reported that these two vectors may exhibit an inclination angle of more than 20° from each other (Karedla et al., Reference Karedla, Stein, Hähnel, Gregor, Chizhik and Enderlein2015) due to the interactions between molecular orbitals and the chemical environment, and the possibility of relaxation into energy states other than
![]() $ {S}_0 $
.
$ {S}_0 $
.
Methods for measuring the orientation of fluorescent molecules
Many methods have been developed to measure the orientation of fluorescent molecules (Rosenberg et al., Reference Rosenberg, Quinlan, Forkey and Goldman2005; Backlund et al., Reference Backlund, Lew, Backer, Sahl and Moerner2014). For example, one can simply add a polarizing beamsplitter (PBS) to a widefield microscope and measure linear dichroism (LD), given by
where
![]() $ \sum {I}_x $
and
$ \sum {I}_x $
and
![]() $ \sum {I}_y $
represent the total numbers of
$ \sum {I}_y $
represent the total numbers of
![]() $ x $
- and
$ x $
- and
![]() $ y $
-polarized emission photons detected. The LD value is an implicit measure of emitter orientation. Further, it has been shown that the rotational mobility of an SM can be determined using the temporal autocorrelation of the LD value (fluorescence anisotropy correlation) (Zondervan et al., Reference Zondervan, Kulzer, Berkhout and Orrit2007). Testa et al. combined SMLM with polarization-sensitive fluorescence detection, showing that 2D histograms of x- and y-polarized fluorescence can reveal the rotational mobility of molecules, as demonstrated in living mammalian cells (Testa et al., Reference Testa, Schönle, Middendorff, Geisler, Medda, Wurm, Stiel, Jakobs, Bossi, Eggeling, Hell SW and Egner2008). However, despite its simplicity, LD suffers from orientational degeneracy, i.e., multiple molecular orientations produce the same LD value, e.g., zero in the cases of
$ y $
-polarized emission photons detected. The LD value is an implicit measure of emitter orientation. Further, it has been shown that the rotational mobility of an SM can be determined using the temporal autocorrelation of the LD value (fluorescence anisotropy correlation) (Zondervan et al., Reference Zondervan, Kulzer, Berkhout and Orrit2007). Testa et al. combined SMLM with polarization-sensitive fluorescence detection, showing that 2D histograms of x- and y-polarized fluorescence can reveal the rotational mobility of molecules, as demonstrated in living mammalian cells (Testa et al., Reference Testa, Schönle, Middendorff, Geisler, Medda, Wurm, Stiel, Jakobs, Bossi, Eggeling, Hell SW and Egner2008). However, despite its simplicity, LD suffers from orientational degeneracy, i.e., multiple molecular orientations produce the same LD value, e.g., zero in the cases of
![]() $ \boldsymbol{\mu} ={\left[\pm 1/\sqrt{2},\pm 1/\sqrt{2},0\right]}^{\top } $
and
$ \boldsymbol{\mu} ={\left[\pm 1/\sqrt{2},\pm 1/\sqrt{2},0\right]}^{\top } $
and
![]() $ \boldsymbol{\mu} ={\left[0,0,1\right]}^{\top } $
. Increasing inclinations out of the xy-plane and increasing wobble also produce LD values closer to zero. To overcome these limitations, one can either manipulate the polarization and/or phase of the collected fluorescence photons (Fourkas, Reference Fourkas2001; Rimoli et al., Reference Rimoli, Valades-Cruz, Curcio, Mavrakis and Brasselet2022) or measure the response of an emitter to various excitation polarizations over time (Forkey et al., Reference Forkey, Quinlan, Alexander Shaw, Corrie and Goldman2003; Beausang et al., Reference Beausang, Shroder, Nelson and Goldman2013; Backer et al., Reference Backer, Biebricher, King, Wuite, Heller and Peterman2019), similar to measuring the polarization of scattered light under various illumination polarizations (Beckwith and Yang, Reference Beckwith and Yang2021).
$ \boldsymbol{\mu} ={\left[0,0,1\right]}^{\top } $
. Increasing inclinations out of the xy-plane and increasing wobble also produce LD values closer to zero. To overcome these limitations, one can either manipulate the polarization and/or phase of the collected fluorescence photons (Fourkas, Reference Fourkas2001; Rimoli et al., Reference Rimoli, Valades-Cruz, Curcio, Mavrakis and Brasselet2022) or measure the response of an emitter to various excitation polarizations over time (Forkey et al., Reference Forkey, Quinlan, Alexander Shaw, Corrie and Goldman2003; Beausang et al., Reference Beausang, Shroder, Nelson and Goldman2013; Backer et al., Reference Backer, Biebricher, King, Wuite, Heller and Peterman2019), similar to measuring the polarization of scattered light under various illumination polarizations (Beckwith and Yang, Reference Beckwith and Yang2021).
Another parameter associated with molecular orientation is fluorescence anisotropy, typically denoted by
![]() $ r $
(not to be confused with position
$ r $
(not to be confused with position
![]() $ \boldsymbol{r} $
) (Harms et al., Reference Harms, Sonnleitner, Schütz, Gruber and Schmidt1999; Gradinaru et al., Reference Gradinaru, Marushchak, Samim and Krull2010). When a molecule is excited by linearly polarized light, fluorescence intensities collected along polarization directions parallel and orthogonal to the illumination are denoted
$ \boldsymbol{r} $
) (Harms et al., Reference Harms, Sonnleitner, Schütz, Gruber and Schmidt1999; Gradinaru et al., Reference Gradinaru, Marushchak, Samim and Krull2010). When a molecule is excited by linearly polarized light, fluorescence intensities collected along polarization directions parallel and orthogonal to the illumination are denoted
![]() $ {I}_{\parallel } $
and
$ {I}_{\parallel } $
and
![]() $ {I}_{\perp } $
, respectively. The fluorescence anisotropy, given by
$ {I}_{\perp } $
, respectively. The fluorescence anisotropy, given by
![]() $ r=\left({I}_{\parallel }-{I}_{\perp}\right)/\left({I}_{\parallel }+2{I}_{\perp}\right) $
, quantifies the degree of rotation a molecule undergoes between absorption and emission. Although the orientation of a molecule cannot be directly measured, anisotropy is extremely sensitive to the rotation of the molecule. An anisotropy value of 0 indicates random emission polarization and free rotational motion, whereas an anisotropy value of 1 represents completely polarized emission from a rotationally fixed emitter. Gould et al. demonstrated (P)-FPALM, a method for simultaneously imaging the positions and anisotropies of single molecules under linearly polarized excitation light, enabling the study of molecular orientations within biological structures, such as mouse fibroblasts expressing Dendra2-actin or Dendra2-hemagglutinin (Gould et al., Reference Gould, Gunewardene, Gudheti, Verkhusha, S-R and Hess2008).
$ r=\left({I}_{\parallel }-{I}_{\perp}\right)/\left({I}_{\parallel }+2{I}_{\perp}\right) $
, quantifies the degree of rotation a molecule undergoes between absorption and emission. Although the orientation of a molecule cannot be directly measured, anisotropy is extremely sensitive to the rotation of the molecule. An anisotropy value of 0 indicates random emission polarization and free rotational motion, whereas an anisotropy value of 1 represents completely polarized emission from a rotationally fixed emitter. Gould et al. demonstrated (P)-FPALM, a method for simultaneously imaging the positions and anisotropies of single molecules under linearly polarized excitation light, enabling the study of molecular orientations within biological structures, such as mouse fibroblasts expressing Dendra2-actin or Dendra2-hemagglutinin (Gould et al., Reference Gould, Gunewardene, Gudheti, Verkhusha, S-R and Hess2008).
A more sophisticated method for measuring molecular orientation involves measuring Stokes parameters (Alonso, Reference Alonso2023), e.g., by using a camera with an integrated polarizer above each pixel (Bruggeman et al., Reference Bruggeman, Zhang, Needham, Körbel, Daly, Cheetham, Peters, Wu, Klymchenko, Davis, Paluch, Klenerman, Lew, O’Holleran and Lee2024) or by using a specific configuration of waveplates and polarizing beamsplitters (Mehta et al., Reference Mehta, McQuilken, La Riviere, Occhipinti, Verma, Oldenbourg, Gladfelter and Tani2016; Rimoli et al., Reference Rimoli, Valades-Cruz, Curcio, Mavrakis and Brasselet2022). Conventionally, the Stokes parameter
![]() $ {s}_0 $
characterizes light intensity, while
$ {s}_0 $
characterizes light intensity, while
![]() $ {s}_1 $
through
$ {s}_1 $
through
![]() $ {s}_3 $
(
$ {s}_3 $
(
![]() $ {s}_8 $
for 3D Stokes parameters) describes light polarization. The degree of linear polarization (DoLP) and angle of linear polarization (AoLP) can be computed using (Bruggeman et al., Reference Bruggeman, Zhang, Needham, Körbel, Daly, Cheetham, Peters, Wu, Klymchenko, Davis, Paluch, Klenerman, Lew, O’Holleran and Lee2024)
$ {s}_8 $
for 3D Stokes parameters) describes light polarization. The degree of linear polarization (DoLP) and angle of linear polarization (AoLP) can be computed using (Bruggeman et al., Reference Bruggeman, Zhang, Needham, Körbel, Daly, Cheetham, Peters, Wu, Klymchenko, Davis, Paluch, Klenerman, Lew, O’Holleran and Lee2024)
 $$ \mathrm{DoLP}=\sqrt{\frac{s_1^2+{s}_2^2}{s_0^2}}\hskip0.6em \mathrm{and} $$
$$ \mathrm{DoLP}=\sqrt{\frac{s_1^2+{s}_2^2}{s_0^2}}\hskip0.6em \mathrm{and} $$
where DoLP is determined by the polar angle
![]() $ \theta $
, and AoLP is equal to the azimuthal angle
$ \theta $
, and AoLP is equal to the azimuthal angle
![]() $ \phi $
. Further, there is an analogy between describing light polarization, which spans from linearly polarized to unpolarized, and the rotational dynamics of a molecule, which can be either fixed in a specific orientation or freely rotating. See “Modeling the rotational diffusion of fluorescent molecules” for more details.
$ \phi $
. Further, there is an analogy between describing light polarization, which spans from linearly polarized to unpolarized, and the rotational dynamics of a molecule, which can be either fixed in a specific orientation or freely rotating. See “Modeling the rotational diffusion of fluorescent molecules” for more details.
In this section, we introduce two major categories of orientation-measurement methods: modulating the polarization of excitation light and detecting the polarization of the emitted fluorescence to measure the absorption dipole moment and modulating fluorescence emission to measure the emission dipole moment. As noted previously, although we classify these methods into absorption and emission-based, these two dipole moments are often coupled in practical experiments. In particular, the alignment of polarized excitation light with the absorption dipole moments can introduce a selection bias, thereby altering the observed distribution of emission dipole moments (Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022; Munger et al., Reference Munger, Sison and Brasselet2023), especially for slowly rotating molecules.
Excitation polarization modulation and polarization-sensitive detection were combined
The principle of measuring the orientation of the absorption dipole moment
![]() $ {\boldsymbol{\mu}}_{\mathrm{abs}} $
using excitation modulation is as described by Eq. (5); an
$ {\boldsymbol{\mu}}_{\mathrm{abs}} $
using excitation modulation is as described by Eq. (5); an
![]() $ x $
-oriented molecule is most likely to absorb an
$ x $
-oriented molecule is most likely to absorb an
![]() $ x $
-polarized photon, and it is impossible for it to absorb a
$ x $
-polarized photon, and it is impossible for it to absorb a
![]() $ y $
- or
$ y $
- or
![]() $ z $
-polarized photon. The analogous statements are true for other polarization-orientation combinations.
$ z $
-polarized photon. The analogous statements are true for other polarization-orientation combinations.
Here, we denote
![]() $ {\boldsymbol{\mu}}_{\mathrm{abs}} $
by
$ {\boldsymbol{\mu}}_{\mathrm{abs}} $
by
![]() $ \boldsymbol{\mu} $
for simplicity. An SM is excited sequentially using illumination light of
$ \boldsymbol{\mu} $
for simplicity. An SM is excited sequentially using illumination light of
![]() $ N $
unique polarizations
$ N $
unique polarizations
![]() $ {\boldsymbol{E}}_1,\dots, {\boldsymbol{E}}_N $
. The expected total number of photons
$ {\boldsymbol{E}}_1,\dots, {\boldsymbol{E}}_N $
. The expected total number of photons
![]() $ {I}_i $
, with
$ {I}_i $
, with
![]() $ i\in \left\{1,2,\dots, N\right\} $
, detected from an SM excited by electric field polarization
$ i\in \left\{1,2,\dots, N\right\} $
, detected from an SM excited by electric field polarization
![]() $ {\boldsymbol{E}}_i $
is given by
$ {\boldsymbol{E}}_i $
is given by
 $$ {\displaystyle \begin{array}{c}{I}_i\propto {\left|\left[\begin{array}{ccc}{E}_{x,i}& {E}_{y,i}& {E}_{z,i}\end{array}\right]{\left[\begin{array}{ccc}{\mu}_x& {\mu}_y& {\mu}_z\end{array}\right]}^{\top}\right|}^2\\ {}=\left[\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{\left|{E}_{x,i}\right|}^2& {\left|{E}_{y,i}\right|}^2\end{array}& {\left|{E}_{z,i}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,i}^{\ast }{E}_{y,i}\right\}\end{array}& 2\operatorname{Re}\left\{{E}_{x,i}^{\ast }{E}_{z,i}\right\}& 2\operatorname{Re}\left\{{E}_{y,i}^{\ast }{E}_{z,i}\right\}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{\mu}_x^2\\ {}{\mu}_y^2\\ {}{\mu}_z^2\end{array}\\ {}\begin{array}{c}{\mu}_x{\mu}_y\\ {}{\mu}_x{\mu}_z\\ {}{\mu}_y{\mu}_z\end{array}\end{array}\right].\end{array}} $$
$$ {\displaystyle \begin{array}{c}{I}_i\propto {\left|\left[\begin{array}{ccc}{E}_{x,i}& {E}_{y,i}& {E}_{z,i}\end{array}\right]{\left[\begin{array}{ccc}{\mu}_x& {\mu}_y& {\mu}_z\end{array}\right]}^{\top}\right|}^2\\ {}=\left[\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{\left|{E}_{x,i}\right|}^2& {\left|{E}_{y,i}\right|}^2\end{array}& {\left|{E}_{z,i}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,i}^{\ast }{E}_{y,i}\right\}\end{array}& 2\operatorname{Re}\left\{{E}_{x,i}^{\ast }{E}_{z,i}\right\}& 2\operatorname{Re}\left\{{E}_{y,i}^{\ast }{E}_{z,i}\right\}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{\mu}_x^2\\ {}{\mu}_y^2\\ {}{\mu}_z^2\end{array}\\ {}\begin{array}{c}{\mu}_x{\mu}_y\\ {}{\mu}_x{\mu}_z\\ {}{\mu}_y{\mu}_z\end{array}\end{array}\right].\end{array}} $$
Since each absorption and emission event arises from a specific molecular orientation
![]() $ \boldsymbol{\mu} $
at time
$ \boldsymbol{\mu} $
at time
![]() $ t $
, any intensity measured using a photon-counting detector can be written as a temporal average over the acquisition interval
$ t $
, any intensity measured using a photon-counting detector can be written as a temporal average over the acquisition interval
![]() $ T $
. Therefore, we define the second-order moments
$ T $
. Therefore, we define the second-order moments
![]() $ \boldsymbol{m}={\left[{m}_{xx},{m}_{yy},{m}_{zz},{m}_{xy},{m}_{xz},{m}_{yz}\right]}^{\top } $
of the transition dipole as
$ \boldsymbol{m}={\left[{m}_{xx},{m}_{yy},{m}_{zz},{m}_{xy},{m}_{xz},{m}_{yz}\right]}^{\top } $
of the transition dipole as
Further, assuming ergodicity,
![]() $ {m}_{ij} $
can also represent a corresponding average in orientation space. The forward imaging model is, therefore, given by
$ {m}_{ij} $
can also represent a corresponding average in orientation space. The forward imaging model is, therefore, given by
 $$ {\displaystyle \begin{array}{c}\boldsymbol{I}=s\left[\begin{array}{c}\begin{array}{c}{I}_1\\ {}{I}_2\end{array}\\ {}\begin{array}{c}\vdots \\ {}{I}_N\end{array}\end{array}\right]\\ {}=s\left[\begin{array}{cc}\begin{array}{ccc}{\left|{E}_{x,1}\right|}^2& {\left|{E}_{y,1}\right|}^2& {\left|{E}_{z,1}\right|}^2\\ {}{\left|{E}_{x,2}\right|}^2& {\left|{E}_{y,2}\right|}^2& {\left|{E}_{z,2}\right|}^2\end{array}& \begin{array}{ccc}2\operatorname{Re}\left\{{E}_{x,1}^{\ast }{E}_{y,1}\right\}& 2\operatorname{Re}\left\{{E}_{x,1}^{\ast }{E}_{z,1}\right\}& 2\operatorname{Re}\left\{{E}_{y,1}^{\ast }{E}_{z,1}\right\}\\ {}2\operatorname{Re}\left\{{E}_{x,2}^{\ast }{E}_{y,2}\right\}& 2\operatorname{Re}\left\{{E}_{x,2}^{\ast }{E}_{z,2}\right\}& 2\operatorname{Re}\left\{{E}_{y,3}^{\ast }{E}_{z,3}\right\}\end{array}\\ {}\begin{array}{ccc}\vdots & \vdots & \vdots \\ {}{\left|{E}_{x,N}\right|}^2& {\left|{E}_{y,N}\right|}^2& {\left|{E}_{z,N}\right|}^2\end{array}& \begin{array}{ccc}\vdots & \vdots & \vdots \\ {}2\operatorname{Re}\left\{{E}_{x,N}^{\ast }{E}_{y,N}\right\}& 2\operatorname{Re}\left\{{E}_{x,N}^{\ast }{E}_{z,N}\right\}& 2\operatorname{Re}\left\{{E}_{y,N}^{\ast }{E}_{z,N}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{m}_{xx}\\ {}{m}_{yy}\\ {}{m}_{zz}\end{array}\\ {}\begin{array}{c}{m}_{xy}\\ {}{m}_{xz}\\ {}{m}_{yz}\end{array}\end{array}\right],\end{array}} $$
$$ {\displaystyle \begin{array}{c}\boldsymbol{I}=s\left[\begin{array}{c}\begin{array}{c}{I}_1\\ {}{I}_2\end{array}\\ {}\begin{array}{c}\vdots \\ {}{I}_N\end{array}\end{array}\right]\\ {}=s\left[\begin{array}{cc}\begin{array}{ccc}{\left|{E}_{x,1}\right|}^2& {\left|{E}_{y,1}\right|}^2& {\left|{E}_{z,1}\right|}^2\\ {}{\left|{E}_{x,2}\right|}^2& {\left|{E}_{y,2}\right|}^2& {\left|{E}_{z,2}\right|}^2\end{array}& \begin{array}{ccc}2\operatorname{Re}\left\{{E}_{x,1}^{\ast }{E}_{y,1}\right\}& 2\operatorname{Re}\left\{{E}_{x,1}^{\ast }{E}_{z,1}\right\}& 2\operatorname{Re}\left\{{E}_{y,1}^{\ast }{E}_{z,1}\right\}\\ {}2\operatorname{Re}\left\{{E}_{x,2}^{\ast }{E}_{y,2}\right\}& 2\operatorname{Re}\left\{{E}_{x,2}^{\ast }{E}_{z,2}\right\}& 2\operatorname{Re}\left\{{E}_{y,3}^{\ast }{E}_{z,3}\right\}\end{array}\\ {}\begin{array}{ccc}\vdots & \vdots & \vdots \\ {}{\left|{E}_{x,N}\right|}^2& {\left|{E}_{y,N}\right|}^2& {\left|{E}_{z,N}\right|}^2\end{array}& \begin{array}{ccc}\vdots & \vdots & \vdots \\ {}2\operatorname{Re}\left\{{E}_{x,N}^{\ast }{E}_{y,N}\right\}& 2\operatorname{Re}\left\{{E}_{x,N}^{\ast }{E}_{z,N}\right\}& 2\operatorname{Re}\left\{{E}_{y,N}^{\ast }{E}_{z,N}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{m}_{xx}\\ {}{m}_{yy}\\ {}{m}_{zz}\end{array}\\ {}\begin{array}{c}{m}_{xy}\\ {}{m}_{xz}\\ {}{m}_{yz}\end{array}\end{array}\right],\end{array}} $$
where
![]() $ s $
is the brightness scaling factor.
$ s $
is the brightness scaling factor.
In the special case where the SMs are only excited by collimated epifluorescence illumination along the
![]() $ z $
direction (optical axis) (Backer et al., Reference Backer, Lee and Moerner2016), the
$ z $
direction (optical axis) (Backer et al., Reference Backer, Lee and Moerner2016), the
![]() $ z $
-polarized component
$ z $
-polarized component
![]() $ {E}_{z,i}=0,\forall i $
. This excitation method is only sensitive to the normalized projection of the orientational second moments into the
$ {E}_{z,i}=0,\forall i $
. This excitation method is only sensitive to the normalized projection of the orientational second moments into the
![]() $ xy $
plane, as given by
$ xy $
plane, as given by
where
 $$ {\displaystyle \begin{array}{c}{\zeta}_i=\frac{\mu_i}{\sqrt{\mu_x^2+{\mu}_y^2}}\hskip0.48em i\in \left\{x,y\right\}.\end{array}} $$
$$ {\displaystyle \begin{array}{c}{\zeta}_i=\frac{\mu_i}{\sqrt{\mu_x^2+{\mu}_y^2}}\hskip0.48em i\in \left\{x,y\right\}.\end{array}} $$
The forward imaging model is simplified as
 $$ {\displaystyle \begin{array}{c}I=s\left[\begin{array}{c}\begin{array}{ccc}{\left|{E}_{x,1}\right|}^2& {\left|{E}_{y,1}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,1}^{\ast }{E}_{y,1}\right\}\\ {}{\left|{E}_{x,2}\right|}^2& {\left|{E}_{y,2}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,2}^{\ast }{E}_{y,2}\right\}\end{array}\\ {}\begin{array}{ccc}\vdots & \vdots & \vdots \\ {}{\left|{E}_{x,N}\right|}^2& {\left|{E}_{y,N}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,N}^{\ast }{E}_{y,N}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}{\zeta}_{xx}\\ {}{\zeta}_{yy}\\ {}{\zeta}_{xy}\end{array}\right].\end{array}} $$
$$ {\displaystyle \begin{array}{c}I=s\left[\begin{array}{c}\begin{array}{ccc}{\left|{E}_{x,1}\right|}^2& {\left|{E}_{y,1}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,1}^{\ast }{E}_{y,1}\right\}\\ {}{\left|{E}_{x,2}\right|}^2& {\left|{E}_{y,2}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,2}^{\ast }{E}_{y,2}\right\}\end{array}\\ {}\begin{array}{ccc}\vdots & \vdots & \vdots \\ {}{\left|{E}_{x,N}\right|}^2& {\left|{E}_{y,N}\right|}^2& 2\operatorname{Re}\left\{{E}_{x,N}^{\ast }{E}_{y,N}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}{\zeta}_{xx}\\ {}{\zeta}_{yy}\\ {}{\zeta}_{xy}\end{array}\right].\end{array}} $$
Using a series of fluorescence images obtained from varying angles of in-plane polarized excitation, achieved by continuously rotating a half-wave plate, Zhanghao et al. demonstrated super-resolution dipole orientation mapping in both fixed and live cells (Zhanghao et al., Reference Zhanghao, Chen, Yang, Wang, Jing, Han, Zhang, Jin, J-T and Xi2016). With three in-plane excitation polarizations that are 60° apart, Backer et al. achieved precisions of 2.5° for the azimuthal angle
![]() $ \phi $
and 22 nm for lateral localization with 8424 signal photons and 158 background photons detected per pixel (Backer et al., Reference Backer, Lee and Moerner2016).
$ \phi $
and 22 nm for lateral localization with 8424 signal photons and 158 background photons detected per pixel (Backer et al., Reference Backer, Lee and Moerner2016).
Note that even though solving the inverse problem associated with Eqs. (14) and (17) is computationally cheap, the main challenge using excitation modulation is that each SM needs to remain in the emissive state with a stable orientation for at least
![]() $ N $
sequential frames. One must also ensure that
$ N $
sequential frames. One must also ensure that
![]() $ {\boldsymbol{E}}_i $
is well known via careful calibration to obtain accurate measurements (Thorsen et al., Reference Thorsen, Hulleman, Rieger and Stallinga2022).
$ {\boldsymbol{E}}_i $
is well known via careful calibration to obtain accurate measurements (Thorsen et al., Reference Thorsen, Hulleman, Rieger and Stallinga2022).
Another challenge of measuring the 3D orientation without measurement degeneracy using the method in Eq. (14) is the complex optical setup required for 3D polarization modulation (Thorsen et al., Reference Thorsen, Hulleman, Rieger and Stallinga2022). One method to overcome this challenge is to combine in-plane excitation polarization modulation [Eq. (17)] with polarized detection. Compared to only using LD [Eq. (10)], the addition of using x- and y-polarized excitation eliminates some measurement degeneracies. For example, the LD values for a rotationally fixed molecule with an orientation of
![]() $ \boldsymbol{\mu} ={\left[1/\sqrt{2},1/\sqrt{2},0\right]}^{\top } $
and a freely wobbling molecule are both zero for unpolarized/circularly polarized excitation. In contrast, the LD value for an isotropic emitter is positive under x-polarized excitation and negative under y-polarized excitation, while the LD values are both zero for the fixed molecule under x- and y-polarized excitation. This method was recently used for measuring the structure of S-DNA (Backer et al., Reference Backer, Biebricher, King, Wuite, Heller and Peterman2019). One can further increase the number of excitation and/or detection polarizations used to eliminate all orientation degeneracies. For example, 8 excitation polarizations and 2 detection polarizations were used to image the walking mechanics of Myosin V (Beausang et al., Reference Beausang, Shroder, Nelson and Goldman2013). Note that since the detected intensities using this method are functions of both the absorption and emission dipole moments, any depolarization, e.g., intramolecular or intermolecular energy transfer (Figure 5c) (Carlsson et al., Reference Carlsson, Larsson, Jonsson, Albinsson and Norden1994), bending of the fluorescent molecule’s backbone due to environmental interactions (Karedla et al., Reference Karedla, Stein, Hähnel, Gregor, Chizhik and Enderlein2015), or rotation during the fluorescence lifetime (Figure 5d), may affect or bias the orientation and wobble measurements (Backer et al., Reference Backer, Biebricher, King, Wuite, Heller and Peterman2019).
$ \boldsymbol{\mu} ={\left[1/\sqrt{2},1/\sqrt{2},0\right]}^{\top } $
and a freely wobbling molecule are both zero for unpolarized/circularly polarized excitation. In contrast, the LD value for an isotropic emitter is positive under x-polarized excitation and negative under y-polarized excitation, while the LD values are both zero for the fixed molecule under x- and y-polarized excitation. This method was recently used for measuring the structure of S-DNA (Backer et al., Reference Backer, Biebricher, King, Wuite, Heller and Peterman2019). One can further increase the number of excitation and/or detection polarizations used to eliminate all orientation degeneracies. For example, 8 excitation polarizations and 2 detection polarizations were used to image the walking mechanics of Myosin V (Beausang et al., Reference Beausang, Shroder, Nelson and Goldman2013). Note that since the detected intensities using this method are functions of both the absorption and emission dipole moments, any depolarization, e.g., intramolecular or intermolecular energy transfer (Figure 5c) (Carlsson et al., Reference Carlsson, Larsson, Jonsson, Albinsson and Norden1994), bending of the fluorescent molecule’s backbone due to environmental interactions (Karedla et al., Reference Karedla, Stein, Hähnel, Gregor, Chizhik and Enderlein2015), or rotation during the fluorescence lifetime (Figure 5d), may affect or bias the orientation and wobble measurements (Backer et al., Reference Backer, Biebricher, King, Wuite, Heller and Peterman2019).
Another advantage of excitation polarization modulation is its compatibility with imaging modalities beyond SMOLM. A recently introduced approach known as MINFLUX-L (minimal photon fluxes – line-shaped dark spots) integrates excitation polarization modulation with MINFLUX (Zhan et al., Reference Zhan, Li, Liu, Sun, He, Kuang and Liu2022). This method uses linearly polarized line-shaped dark spots to probe molecules, thereby estimating 2D positions (
![]() $ {\sigma}_{xy}=12.3 $
nm) and azimuthal angles (
$ {\sigma}_{xy}=12.3 $
nm) and azimuthal angles (
![]() $ {\sigma}_{\phi }={26.6}^{\circ } $
) using only 15 detected photons. Excitation modulation is also compatible with super-resolution techniques that image multiple fluorophores at once. For example, in optical lock-in detection super-resolution dipole orientation mapping (OLID-SDOM) (Guan et al., Reference Guan, Wang, Zhanghao, Zhang, Li, Liu, Niu, Yang, Chen, Jing, Zhang, Jin, Xi and Gao2022), a continuously rotating excitation polarization is used to achieve background suppression and enable orientation measurements.
$ {\sigma}_{\phi }={26.6}^{\circ } $
) using only 15 detected photons. Excitation modulation is also compatible with super-resolution techniques that image multiple fluorophores at once. For example, in optical lock-in detection super-resolution dipole orientation mapping (OLID-SDOM) (Guan et al., Reference Guan, Wang, Zhanghao, Zhang, Li, Liu, Niu, Yang, Chen, Jing, Zhang, Jin, Xi and Gao2022), a continuously rotating excitation polarization is used to achieve background suppression and enable orientation measurements.
An attempt to achieve super-resolution using polarized excitation was proposed by Hafi et al. (Reference Hafi, Grunwald, Van Den Heuvel, Aspelmeier, Chen, Zagrebelsky, Schütte, Steinem, Korte, Munk and Walla2014). This method leverages the different responses of dipole emitters to varying excitation polarizations to distinguish between closely positioned molecules with different orientations and thereby improve resolution beyond the diffraction limit. However, its feasibility was questioned, especially when the orientation of emitters within a diffraction-limited area is homogeneous (Frahm and Keller, Reference Frahm and Keller2016). In response to these concerns, Hafi et al. acknowledged that the conditions necessary for resolution improvement via excitation polarization modulation require further investigation (Hafi et al., Reference Hafi, Grunwald, Van Den Heuvel, Aspelmeier, Steinem, Korte, Munk and Walla2016).
Back focal plane imaging
To measure the emission dipole moment of fluorescent molecules, a forward imaging model that maps
![]() $ {\boldsymbol{\mu}}_{\mathrm{em}} $
to the measurement space is required. The theory of image formation of dipole emitters has been discussed in many works (Böhmer and Enderlein, Reference Böhmer and Enderlein2003; Lieb et al., Reference Lieb, Zavislan and Novotny2004; Axelrod, Reference Axelrod2012; Novotny and Hecht, Reference Novotny and Hecht2012; Backer and Moerner, Reference Backer and Moerner2014, Reference Backer and Moerner2015; Chandler et al., Reference Chandler, Shroff, Oldenbourg and La Rivière2019a). Here, we briefly derive the forward imaging model for two important cases that arise from Eq. (6): a matched case, where the SM is embedded within a homogeneous environment whose refractive index (RI) matches that of the objective lens immersion medium (Figure 6a), and a mismatched case, where the SM is embedded in a sample environment with an RI (
$ {\boldsymbol{\mu}}_{\mathrm{em}} $
to the measurement space is required. The theory of image formation of dipole emitters has been discussed in many works (Böhmer and Enderlein, Reference Böhmer and Enderlein2003; Lieb et al., Reference Lieb, Zavislan and Novotny2004; Axelrod, Reference Axelrod2012; Novotny and Hecht, Reference Novotny and Hecht2012; Backer and Moerner, Reference Backer and Moerner2014, Reference Backer and Moerner2015; Chandler et al., Reference Chandler, Shroff, Oldenbourg and La Rivière2019a). Here, we briefly derive the forward imaging model for two important cases that arise from Eq. (6): a matched case, where the SM is embedded within a homogeneous environment whose refractive index (RI) matches that of the objective lens immersion medium (Figure 6a), and a mismatched case, where the SM is embedded in a sample environment with an RI (
![]() $ {n}_2 $
) different from that of the immersion medium (
$ {n}_2 $
) different from that of the immersion medium (
![]() $ {n}_1 $
, Figure 6b). For simplicity, we denote
$ {n}_1 $
, Figure 6b). For simplicity, we denote
![]() $ {\boldsymbol{\mu}}_{\mathrm{em}} $
by
$ {\boldsymbol{\mu}}_{\mathrm{em}} $
by
![]() $ \boldsymbol{\mu} $
in this section.
$ \boldsymbol{\mu} $
in this section.
We first evaluate the case where the sample RI (
![]() $ {n}_1 $
) matches that of the immersion medium (
$ {n}_1 $
) matches that of the immersion medium (
![]() $ {n}_2 $
). We denote the direction of the s- and p-polarized light using unit vectors (Figure 6a)
$ {n}_2 $
). We denote the direction of the s- and p-polarized light using unit vectors (Figure 6a)
where
![]() $ {\theta}_{\mathrm{ff}} $
and
$ {\theta}_{\mathrm{ff}} $
and
![]() $ {\phi}_{\mathrm{ff}} $
are the polar and azimuthal angles associated with the propagation direction
$ {\phi}_{\mathrm{ff}} $
are the polar and azimuthal angles associated with the propagation direction
![]() $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $
[Eq. (7)]. The far-field emission can be written as
$ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $
[Eq. (7)]. The far-field emission can be written as
where scalars
represent the amplitudes of the s- and p-polarized light observed from direction
![]() $ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $
, respectively. The objective lens collects this fluorescence and collimates it such that it propagates parallel to the optical axis. That is, p-polarized light within the sample is rotated to a polarization along the direction
$ {\hat{\boldsymbol{r}}}_{\mathrm{ff}} $
, respectively. The objective lens collects this fluorescence and collimates it such that it propagates parallel to the optical axis. That is, p-polarized light within the sample is rotated to a polarization along the direction
with polar coordinates within the back focal plane (BFP) expressed as
![]() $ {\rho}_{\mathrm{BFP}}={f}_{\mathrm{OL}}\sin {\theta}_{\mathrm{ff}} $
and
$ {\rho}_{\mathrm{BFP}}={f}_{\mathrm{OL}}\sin {\theta}_{\mathrm{ff}} $
and
![]() $ {\phi}_{\mathrm{BFP}}={\phi}_{\mathrm{ff}} $
and
$ {\phi}_{\mathrm{BFP}}={\phi}_{\mathrm{ff}} $
and
![]() $ {f}_{\mathrm{OL}} $
denoting the focal length of the objective lens. Therefore, the optical field at the BFP is given by
$ {f}_{\mathrm{OL}} $
denoting the focal length of the objective lens. Therefore, the optical field at the BFP is given by
 $$ {\displaystyle \begin{array}{c}\hskip-11.5pc {\boldsymbol{E}}_{\mathrm{BFP}}\left({\rho}_{\mathrm{BFP}},{\phi}_{\mathrm{BFP}}\right)={A}_s{\boldsymbol{\nu}}_s+{A}_p{\boldsymbol{\nu}}_r\\ {}={c}_{\mathrm{BFP}}\mathrm{Circ}\left(\frac{\rho_{\mathrm{BFP}}{n}_1}{\hskip0.35em {f}_{\mathrm{OL}}\mathrm{NA}}\right){\left(\cos {\theta}_{\mathrm{ff}}\right)}^{-1/2}\left({\boldsymbol{\nu}}_s{\boldsymbol{\nu}}_s^{\top }+{\boldsymbol{\nu}}_r{\boldsymbol{\nu}}_p^{\top}\right)\left(\unicode{x1D540}-{\hat{\boldsymbol{r}}}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top}\right)\boldsymbol{\mu} \\ {}\hskip-17pc ={\boldsymbol{G}}_{BFP}\boldsymbol{\mu}, \end{array}} $$
$$ {\displaystyle \begin{array}{c}\hskip-11.5pc {\boldsymbol{E}}_{\mathrm{BFP}}\left({\rho}_{\mathrm{BFP}},{\phi}_{\mathrm{BFP}}\right)={A}_s{\boldsymbol{\nu}}_s+{A}_p{\boldsymbol{\nu}}_r\\ {}={c}_{\mathrm{BFP}}\mathrm{Circ}\left(\frac{\rho_{\mathrm{BFP}}{n}_1}{\hskip0.35em {f}_{\mathrm{OL}}\mathrm{NA}}\right){\left(\cos {\theta}_{\mathrm{ff}}\right)}^{-1/2}\left({\boldsymbol{\nu}}_s{\boldsymbol{\nu}}_s^{\top }+{\boldsymbol{\nu}}_r{\boldsymbol{\nu}}_p^{\top}\right)\left(\unicode{x1D540}-{\hat{\boldsymbol{r}}}_{\mathrm{ff}}{\hat{\boldsymbol{r}}}_{\mathrm{ff}}^{\top}\right)\boldsymbol{\mu} \\ {}\hskip-17pc ={\boldsymbol{G}}_{BFP}\boldsymbol{\mu}, \end{array}} $$
where the scalar
![]() $ {c}_{\mathrm{BFP}} $
is a normalization factor (set to 1 here—the field may be normalized further) and NA is the numerical aperture of the objective. The circular indicator function
$ {c}_{\mathrm{BFP}} $
is a normalization factor (set to 1 here—the field may be normalized further) and NA is the numerical aperture of the objective. The circular indicator function
![]() $ \mathrm{Circ}\left(\rho \right) $
represents a finite aperture and is equal to 1 for
$ \mathrm{Circ}\left(\rho \right) $
represents a finite aperture and is equal to 1 for
![]() $ \rho <1 $
and 0 otherwise. The apodization factor
$ \rho <1 $
and 0 otherwise. The apodization factor
![]() $ {\left(\cos {\theta}_{\mathrm{ff}}\right)}^{-1/2} $
maps the equal-angular distribution of energy in object space to a planar projection on the BFP while guaranteeing that the total energy entering the objective lens is identical to that within the BFP. That is,
$ {\left(\cos {\theta}_{\mathrm{ff}}\right)}^{-1/2} $
maps the equal-angular distribution of energy in object space to a planar projection on the BFP while guaranteeing that the total energy entering the objective lens is identical to that within the BFP. That is,
 $$ {\displaystyle \begin{array}{c}\hskip-3em {\int}_{\phi_{\mathrm{ff}}=0}^{2\pi }{\int}_{\theta_{\mathrm{ff}}=0}^{\theta_0}{\left|{\boldsymbol{E}}_{\mathrm{ff}}\right|}^2\sin {\theta}_{\mathrm{ff}}\mathrm{d}{\theta}_{\mathrm{ff}}\;\mathrm{d}{\phi}_{\mathrm{ff}}\\ {}={\int}_{\phi_{\mathrm{BFP}}=0}^{2\pi }{\int}_{\rho_{\mathrm{BFP}}=0}^{f_{\mathrm{OL}}{\theta}_0}{\left|{\boldsymbol{E}}_{\mathrm{BFP}}\right|}^2{\rho}_{\mathrm{BFP}}\;\mathrm{d}{\rho}_{\mathrm{BFP}}\;\mathrm{d}{\phi}_{\mathrm{BFP}},\end{array}} $$
$$ {\displaystyle \begin{array}{c}\hskip-3em {\int}_{\phi_{\mathrm{ff}}=0}^{2\pi }{\int}_{\theta_{\mathrm{ff}}=0}^{\theta_0}{\left|{\boldsymbol{E}}_{\mathrm{ff}}\right|}^2\sin {\theta}_{\mathrm{ff}}\mathrm{d}{\theta}_{\mathrm{ff}}\;\mathrm{d}{\phi}_{\mathrm{ff}}\\ {}={\int}_{\phi_{\mathrm{BFP}}=0}^{2\pi }{\int}_{\rho_{\mathrm{BFP}}=0}^{f_{\mathrm{OL}}{\theta}_0}{\left|{\boldsymbol{E}}_{\mathrm{BFP}}\right|}^2{\rho}_{\mathrm{BFP}}\;\mathrm{d}{\rho}_{\mathrm{BFP}}\;\mathrm{d}{\phi}_{\mathrm{BFP}},\end{array}} $$
where
Representative images of the intensity distribution given by Eq. (22) at the BFP for several molecular orientations are shown in Figure 6d.
Next, we evaluate the case when the sample RI differs from that of the immersion medium, which usually happens during typical biological imaging; the sample’s RI is often close to that of water (
![]() $ {n}_2=1.33 $
), whereas the immersion medium often has a larger RI (e.g.,
$ {n}_2=1.33 $
), whereas the immersion medium often has a larger RI (e.g.,
![]() $ {n}_1=1.515 $
) in order to achieve a higher collection NA. We define the following unit vectors (Figure 6b)
$ {n}_1=1.515 $
) in order to achieve a higher collection NA. We define the following unit vectors (Figure 6b)
to represent the directions of p-polarized light within the lens immersion medium (
![]() $ {n}_1 $
) and sample (
$ {n}_1 $
) and sample (
![]() $ {n}_2 $
). Propagation directions
$ {n}_2 $
). Propagation directions
![]() $ {\theta}_{\mathrm{ff},1} $
and
$ {\theta}_{\mathrm{ff},1} $
and
![]() $ {\theta}_{\mathrm{ff},2} $
are related by
$ {\theta}_{\mathrm{ff},2} $
are related by
according to Snell’s law. The polarization direction of the s-polarized light remains unchanged. The fields immediately before (
![]() $ {\boldsymbol{E}}_{\mathrm{ff},2} $
) and after (
$ {\boldsymbol{E}}_{\mathrm{ff},2} $
) and after (
![]() $ {\boldsymbol{E}}_{\mathrm{ff},1} $
) propagating through the RI interface are written as (Figure 6b)
$ {\boldsymbol{E}}_{\mathrm{ff},1} $
) propagating through the RI interface are written as (Figure 6b)
where from Eq. (6), we have
![]() $ {c}_{\mathrm{ff},2} $
is a normalization factor, and
$ {c}_{\mathrm{ff},2} $
is a normalization factor, and
are the Fresnel transmission coefficients for s- and p-polarized light. The field right before entering the objective lens is, therefore, given by
where
![]() $ \cos {\theta}_{\mathrm{ff},1} $
and
$ \cos {\theta}_{\mathrm{ff},1} $
and
![]() $ \cos {\theta}_{\mathrm{ff},2} $
represent the amplitude normalization factors corresponding to the spherical waves and
$ \cos {\theta}_{\mathrm{ff},2} $
represent the amplitude normalization factors corresponding to the spherical waves and
![]() $ {c}_{\mathrm{ff},1} $
(assumed to be 1 here) is a normalization factor. Similar to Eq. (22), accounting for the apodization factor, the optical field observed at the BFP is given by
$ {c}_{\mathrm{ff},1} $
(assumed to be 1 here) is a normalization factor. Similar to Eq. (22), accounting for the apodization factor, the optical field observed at the BFP is given by
 $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{BFP}}\left(u,v\right)\\ {}={c}_{\mathrm{BFP}}\mathrm{Circ}\left(\frac{\rho_{\mathrm{BFP}}{n}_1}{\hskip0.35em {f}_{\mathrm{OL}}\mathrm{NA}}\right)\frac{{\left(\cos {\theta}_{\mathrm{ff},1}\right)}^{\frac{1}{2}}}{\cos {\theta}_{\mathrm{ff},2}}\left({t}_s{\boldsymbol{\nu}}_s{\boldsymbol{\nu}}_s^{\top }+{t}_p{\boldsymbol{\nu}}_r{\boldsymbol{\nu}}_{p,2}^{\top}\right)\left(\unicode{x1D540}-{\hat{\boldsymbol{r}}}_{\mathrm{ff},2}{\hat{\boldsymbol{r}}}_{\mathrm{ff},2}^{\top}\right)\\ {}\boldsymbol{\mu} ={\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu} \\ {}=\left[\begin{array}{ccc}{g}_x^{(x)}\left(u,v\right)& {g}_y^{(x)}\left(u,v\right)& {g}_z^{(x)}\left(u,v\right)\\ {}{g}_x^{(y)}\left(u,v\right)& {g}_y^{(y)}\left(u,v\right)& {g}_z^{(y)}\left(u,v\right)\\ {}0& 0& 0\end{array}\right]\boldsymbol{\mu}, \end{array}} $$
$$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{BFP}}\left(u,v\right)\\ {}={c}_{\mathrm{BFP}}\mathrm{Circ}\left(\frac{\rho_{\mathrm{BFP}}{n}_1}{\hskip0.35em {f}_{\mathrm{OL}}\mathrm{NA}}\right)\frac{{\left(\cos {\theta}_{\mathrm{ff},1}\right)}^{\frac{1}{2}}}{\cos {\theta}_{\mathrm{ff},2}}\left({t}_s{\boldsymbol{\nu}}_s{\boldsymbol{\nu}}_s^{\top }+{t}_p{\boldsymbol{\nu}}_r{\boldsymbol{\nu}}_{p,2}^{\top}\right)\left(\unicode{x1D540}-{\hat{\boldsymbol{r}}}_{\mathrm{ff},2}{\hat{\boldsymbol{r}}}_{\mathrm{ff},2}^{\top}\right)\\ {}\boldsymbol{\mu} ={\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu} \\ {}=\left[\begin{array}{ccc}{g}_x^{(x)}\left(u,v\right)& {g}_y^{(x)}\left(u,v\right)& {g}_z^{(x)}\left(u,v\right)\\ {}{g}_x^{(y)}\left(u,v\right)& {g}_y^{(y)}\left(u,v\right)& {g}_z^{(y)}\left(u,v\right)\\ {}0& 0& 0\end{array}\right]\boldsymbol{\mu}, \end{array}} $$
where
Entries
![]() $ {g}_i^{(j)} $
, with
$ {g}_i^{(j)} $
, with
![]() $ i,j\in \left\{x,y,z\right\} $
, are termed the (
$ i,j\in \left\{x,y,z\right\} $
, are termed the (
![]() $ j $
-polarized) basis fields at the BFP. They represent the fields produced by
$ j $
-polarized) basis fields at the BFP. They represent the fields produced by
![]() $ x $
-,
$ x $
-,
![]() $ y $
-, and
$ y $
-, and
![]() $ z $
-oriented dipoles, and any intermediate orientation
$ z $
-oriented dipoles, and any intermediate orientation
![]() $ \boldsymbol{\mu} $
produces a linear combination of these basis fields
$ \boldsymbol{\mu} $
produces a linear combination of these basis fields
![]() $ {g}_i $
.
$ {g}_i $
.
Finally, for a molecule located at
![]() $ \boldsymbol{r}={\left[x,y,{z}_{\mathrm{SM}}\right]}^{\top } $
, where
$ \boldsymbol{r}={\left[x,y,{z}_{\mathrm{SM}}\right]}^{\top } $
, where
![]() $ {z}_{\mathrm{SM}} $
(Figure 6c) is the distance of the SM to the RI interface from above, the electric field at the BFP is given by
$ {z}_{\mathrm{SM}} $
(Figure 6c) is the distance of the SM to the RI interface from above, the electric field at the BFP is given by
 $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{BFP}}\left(u,v;\boldsymbol{r},\boldsymbol{\mu} \right)=\\ {}\exp \left[\frac{j2\pi }{\lambda}\left({n}_1 xu+{n}_1 yv-{n}_1{z}_f\cos {\theta}_{ff,1}+{n}_2{z}_{\mathrm{SM}}\cos {\theta}_{ff,2}\right)\right]{\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu} \\ {}=\exp \left\{\frac{j2\pi {n}_1}{\lambda}\left[ xu+ yv-{z}_f\sqrt{1-{u}^2-{v}^2}+{z}_{\mathrm{SM}}\sqrt{{\left(\frac{n_2}{n_1}\right)}^2-{u}^2-{v}^2}\right]\right\}{\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu}, \end{array}} $$
$$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{BFP}}\left(u,v;\boldsymbol{r},\boldsymbol{\mu} \right)=\\ {}\exp \left[\frac{j2\pi }{\lambda}\left({n}_1 xu+{n}_1 yv-{n}_1{z}_f\cos {\theta}_{ff,1}+{n}_2{z}_{\mathrm{SM}}\cos {\theta}_{ff,2}\right)\right]{\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu} \\ {}=\exp \left\{\frac{j2\pi {n}_1}{\lambda}\left[ xu+ yv-{z}_f\sqrt{1-{u}^2-{v}^2}+{z}_{\mathrm{SM}}\sqrt{{\left(\frac{n_2}{n_1}\right)}^2-{u}^2-{v}^2}\right]\right\}{\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu}, \end{array}} $$
where
![]() $ {z}_f $
represents the position of the nominal focal plane above the RI interface. We note that Eq. (33) assumes an ideal objective lens, and any (possibly field-dependent) optical aberrations (Fu et al., Reference Fu, Shi, Luo, He, Zhou, Yang, Yang, Liu, Liu, Guo, Yang, Liu, Huang, Ries, Zhang, Xi, Jin and Li2023; Liu et al., Reference Liu, Chen, Hellgoth, Müller, Ferdman, Karras, Xiao, Lidke, Heintzmann, Shechtman, Li and Ries2024; Xiao et al., Reference Xiao, Kedem Orange, Opatovski, Parizat, Nehme, Alalouf and Shechtman2024; Xu et al., Reference Xu, Ma, MacPherson, Liu, Bu, Wang, Tang, Bi, Kwok, Chubykin, Yin, Calve, Landreth and Huang2020) can change the amplitude or phase or both of
$ {z}_f $
represents the position of the nominal focal plane above the RI interface. We note that Eq. (33) assumes an ideal objective lens, and any (possibly field-dependent) optical aberrations (Fu et al., Reference Fu, Shi, Luo, He, Zhou, Yang, Yang, Liu, Liu, Guo, Yang, Liu, Huang, Ries, Zhang, Xi, Jin and Li2023; Liu et al., Reference Liu, Chen, Hellgoth, Müller, Ferdman, Karras, Xiao, Lidke, Heintzmann, Shechtman, Li and Ries2024; Xiao et al., Reference Xiao, Kedem Orange, Opatovski, Parizat, Nehme, Alalouf and Shechtman2024; Xu et al., Reference Xu, Ma, MacPherson, Liu, Bu, Wang, Tang, Bi, Kwok, Chubykin, Yin, Calve, Landreth and Huang2020) can change the amplitude or phase or both of
![]() $ {\boldsymbol{E}}_{\mathrm{BFP}}\left(u,v;\boldsymbol{r},\boldsymbol{\mu} \right) $
.
$ {\boldsymbol{E}}_{\mathrm{BFP}}\left(u,v;\boldsymbol{r},\boldsymbol{\mu} \right) $
.
The intensity of x- and y-polarized fluorescence at the BFP is given by
 $$ {\displaystyle \begin{array}{c}\left[\begin{array}{c}{I}_x\\ {}{I}_y\end{array}\right]=\\ {}s\left[\begin{array}{cc}\begin{array}{ccc}{\left|{g}_x^{(x)}\right|}^2& {\left|{g}_y^{(x)}\right|}^2& {\left|{g}_z^{(x)}\right|}^2\\ {}{\left|{g}_x^{(y)}\right|}^2& {\left|{g}_y^{(y)}\right|}^2& {\left|{g}_z^{(y)}\right|}^2\end{array}& \begin{array}{ccc}2\operatorname{Re}\left\{{g}_x^{(x)\ast }{g}_y^{(x)}\right\}& 2\operatorname{Re}\left\{{g}_x^{(x)\ast }{g}_z^{(x)}\right\}& 2\operatorname{Re}\left\{{g}_y^{(x)\ast }{g}_z^{(x)}\right\}\\ {}2\operatorname{Re}\left\{{g}_x^{(y)\ast }{g}_y^{(y)}\right\}& 2\operatorname{Re}\left\{{g}_x^{(y)\ast }{g}_z^{(y)}\right\}& 2\operatorname{Re}\left\{{g}_y^{(y)\ast }{g}_z^{(y)}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{m}_{xx}\\ {}{m}_{yy}\\ {}{m}_{zz}\end{array}\\ {}\begin{array}{c}{m}_{xy}\\ {}{m}_{xz}\\ {}{m}_{yz}\end{array}\end{array}\right].\\ {}\end{array}} $$
$$ {\displaystyle \begin{array}{c}\left[\begin{array}{c}{I}_x\\ {}{I}_y\end{array}\right]=\\ {}s\left[\begin{array}{cc}\begin{array}{ccc}{\left|{g}_x^{(x)}\right|}^2& {\left|{g}_y^{(x)}\right|}^2& {\left|{g}_z^{(x)}\right|}^2\\ {}{\left|{g}_x^{(y)}\right|}^2& {\left|{g}_y^{(y)}\right|}^2& {\left|{g}_z^{(y)}\right|}^2\end{array}& \begin{array}{ccc}2\operatorname{Re}\left\{{g}_x^{(x)\ast }{g}_y^{(x)}\right\}& 2\operatorname{Re}\left\{{g}_x^{(x)\ast }{g}_z^{(x)}\right\}& 2\operatorname{Re}\left\{{g}_y^{(x)\ast }{g}_z^{(x)}\right\}\\ {}2\operatorname{Re}\left\{{g}_x^{(y)\ast }{g}_y^{(y)}\right\}& 2\operatorname{Re}\left\{{g}_x^{(y)\ast }{g}_z^{(y)}\right\}& 2\operatorname{Re}\left\{{g}_y^{(y)\ast }{g}_z^{(y)}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{m}_{xx}\\ {}{m}_{yy}\\ {}{m}_{zz}\end{array}\\ {}\begin{array}{c}{m}_{xy}\\ {}{m}_{xz}\\ {}{m}_{yz}\end{array}\end{array}\right].\\ {}\end{array}} $$
Representative images of the intensity distribution given by Eqs. (31) and (32) at the BFP are shown in Figure 6e,f. The molecule is located at
![]() $ \boldsymbol{r}={\left[0,0,0\right]}^{\top } $
and the nominal focal plane position
$ \boldsymbol{r}={\left[0,0,0\right]}^{\top } $
and the nominal focal plane position
![]() $ {z}_f=0 $
. The bright ring in these images represents the supercritical light coming from the evanescent fields near the SM that are transformed into propagating waves in the immersion medium (Axelrod, Reference Axelrod2012). These intensity patterns can directly be used to measure the orientation of fluorophores (Lieb et al., Reference Lieb, Zavislan and Novotny2004).
$ {z}_f=0 $
. The bright ring in these images represents the supercritical light coming from the evanescent fields near the SM that are transformed into propagating waves in the immersion medium (Axelrod, Reference Axelrod2012). These intensity patterns can directly be used to measure the orientation of fluorophores (Lieb et al., Reference Lieb, Zavislan and Novotny2004).
Modeling the rotational diffusion of fluorescent molecules
According to Eqs. (14) and (34), optical imaging is sensitive to the second-order orientational moments
![]() $ \boldsymbol{m} $
of SMs instead of their first-order transition dipole moments
$ \boldsymbol{m} $
of SMs instead of their first-order transition dipole moments
![]() $ \boldsymbol{\mu} $
. To interpret these values of
$ \boldsymbol{\mu} $
. To interpret these values of
![]() $ \boldsymbol{m} $
, several models have been proposed to describe dipole orientation and wobble. One approach is to first rearrange the second moments into a 3 × 3 positive semidefinite (Zhou et al., Reference Zhou, Wu and Lew2024b) Hermitian matrix
$ \boldsymbol{m} $
, several models have been proposed to describe dipole orientation and wobble. One approach is to first rearrange the second moments into a 3 × 3 positive semidefinite (Zhou et al., Reference Zhou, Wu and Lew2024b) Hermitian matrix
![]() $ \boldsymbol{M} $
, which can be decomposed as
$ \boldsymbol{M} $
, which can be decomposed as
 $$ {\displaystyle \begin{array}{c}\boldsymbol{M}=\left[\begin{array}{ccc}{m}_{xx}& {m}_{xy}& {m}_{xz}\\ {}{m}_{xy}& {m}_{yy}& {m}_{yz}\\ {}{m}_{xz}& {m}_{yz}& {m}_{zz}\end{array}\right]={\sum}_{i=1}^3{\lambda}_i{\boldsymbol{\nu}}_i{\boldsymbol{\nu}}_i^{\top}\\ {}=\frac{3{\lambda}_1-1}{2}{\boldsymbol{\nu}}_1{\boldsymbol{\nu}}_1^{\top }+\frac{3-3{\lambda}_1}{2}\frac{\unicode{x1D540}}{3}+\frac{\lambda_2-{\lambda}_3}{2}\left({\boldsymbol{\nu}}_2{\boldsymbol{\nu}}_2^{\top }-{\boldsymbol{\nu}}_3{\boldsymbol{\nu}}_3^{\top}\right),\end{array}} $$
$$ {\displaystyle \begin{array}{c}\boldsymbol{M}=\left[\begin{array}{ccc}{m}_{xx}& {m}_{xy}& {m}_{xz}\\ {}{m}_{xy}& {m}_{yy}& {m}_{yz}\\ {}{m}_{xz}& {m}_{yz}& {m}_{zz}\end{array}\right]={\sum}_{i=1}^3{\lambda}_i{\boldsymbol{\nu}}_i{\boldsymbol{\nu}}_i^{\top}\\ {}=\frac{3{\lambda}_1-1}{2}{\boldsymbol{\nu}}_1{\boldsymbol{\nu}}_1^{\top }+\frac{3-3{\lambda}_1}{2}\frac{\unicode{x1D540}}{3}+\frac{\lambda_2-{\lambda}_3}{2}\left({\boldsymbol{\nu}}_2{\boldsymbol{\nu}}_2^{\top }-{\boldsymbol{\nu}}_3{\boldsymbol{\nu}}_3^{\top}\right),\end{array}} $$
where
![]() $ \unicode{x1D540} $
represents the identity matrix and the scalars
$ \unicode{x1D540} $
represents the identity matrix and the scalars
![]() $ {\lambda}_i $
and vectors
$ {\lambda}_i $
and vectors
![]() $ {\boldsymbol{\nu}}_i $
correspond to the ith eigenvalue and eigenvector of
$ {\boldsymbol{\nu}}_i $
correspond to the ith eigenvalue and eigenvector of
![]() $ \boldsymbol{M} $
, in the order of descending
$ \boldsymbol{M} $
, in the order of descending
![]() $ {\lambda}_i $
. Therefore, the second moments
$ {\lambda}_i $
. Therefore, the second moments
![]() $ \boldsymbol{M} $
perceived by the imaging system may be interpreted as a weighted mixture of several components: a fixed dipole of orientation
$ \boldsymbol{M} $
perceived by the imaging system may be interpreted as a weighted mixture of several components: a fixed dipole of orientation
![]() $ \boldsymbol{\mu} ={\boldsymbol{\nu}}_1 $
, an isotropic emitter (
$ \boldsymbol{\mu} ={\boldsymbol{\nu}}_1 $
, an isotropic emitter (
![]() $ \unicode{x1D540}/3 $
), and an orthogonal nuisance term that arises from asymmetric rotation.
$ \unicode{x1D540}/3 $
), and an orthogonal nuisance term that arises from asymmetric rotation.
If the molecule diffuses in all directions equally (Zhang and Lew, Reference Zhang and Lew2019), thereby exhibiting isotropic rotational diffusion, then the smaller eigenvalues
![]() $ {\lambda}_2 $
and
$ {\lambda}_2 $
and
![]() $ {\lambda}_3 $
are identical. We may define rotational constraint
$ {\lambda}_3 $
are identical. We may define rotational constraint
![]() $ \gamma =\left(3{\lambda}_1-1\right)/2 $
such that
$ \gamma =\left(3{\lambda}_1-1\right)/2 $
such that
where the individual second moments are given by
The rotational constraint
![]() $ \gamma \in \left[0,1\right] $
represents the degree to which the molecule’s emission is consistent with a fixed dipole (Backer and Moerner, Reference Backer and Moerner2014, Reference Backer and Moerner2015; Backer et al., Reference Backer, Lee and Moerner2016);
$ \gamma \in \left[0,1\right] $
represents the degree to which the molecule’s emission is consistent with a fixed dipole (Backer and Moerner, Reference Backer and Moerner2014, Reference Backer and Moerner2015; Backer et al., Reference Backer, Lee and Moerner2016);
![]() $ \gamma =0 $
represents an isotropic emitter. We may parameterize this isotropic rotational diffusion as uniform wobble within a hard-edged cone of half angle
$ \gamma =0 $
represents an isotropic emitter. We may parameterize this isotropic rotational diffusion as uniform wobble within a hard-edged cone of half angle
![]() $ {\alpha}_s $
, and thus,
$ {\alpha}_s $
, and thus,
![]() $ \gamma $
can be written as
$ \gamma $
can be written as
 $$ {\displaystyle \begin{array}{c}\gamma =1-3{m}_{xx{\left(\right|}_{{\boldsymbol{\unicode{x03BD}}}_1={\left[0,0,1\right]}^{\top }}}\\ {}=1-\frac{3\int_0^{\alpha_s}{\int}_0^{2\unicode{x03C0}}{\left(\sin {\theta}^{\prime}\cos {\phi}^{\prime}\right)}^2\sin {\theta}^{\prime }d{\phi}^{\prime }d{\theta}^{\prime }}{\int_0^{\alpha_s}{\int}_0^{2\unicode{x03C0}}\sin {\theta}^{\prime }d{\phi}^{\prime }d{\theta}^{\prime }}=\frac{\cos^2{\alpha}_s+\cos {\alpha}_s}{2}.\end{array}} $$
$$ {\displaystyle \begin{array}{c}\gamma =1-3{m}_{xx{\left(\right|}_{{\boldsymbol{\unicode{x03BD}}}_1={\left[0,0,1\right]}^{\top }}}\\ {}=1-\frac{3\int_0^{\alpha_s}{\int}_0^{2\unicode{x03C0}}{\left(\sin {\theta}^{\prime}\cos {\phi}^{\prime}\right)}^2\sin {\theta}^{\prime }d{\phi}^{\prime }d{\theta}^{\prime }}{\int_0^{\alpha_s}{\int}_0^{2\unicode{x03C0}}\sin {\theta}^{\prime }d{\phi}^{\prime }d{\theta}^{\prime }}=\frac{\cos^2{\alpha}_s+\cos {\alpha}_s}{2}.\end{array}} $$
Alternatively, Eq. (38) is equivalent to
where
![]() $ \varOmega \in \left[0,2\unicode{x03C0} \right] $
represents the solid angle subtended by the cone on the orientation hemisphere (Figure 5a). A rotationally fixed molecule has a cone solid angle of 0, while a freely rotating molecule has
$ \varOmega \in \left[0,2\unicode{x03C0} \right] $
represents the solid angle subtended by the cone on the orientation hemisphere (Figure 5a). A rotationally fixed molecule has a cone solid angle of 0, while a freely rotating molecule has
![]() $ \varOmega =2\unicode{x03C0} $
.
$ \varOmega =2\unicode{x03C0} $
.
Ding et al. and Zhou et al. further investigated molecules exhibiting anisotropic wobble, specifically focusing on scenarios where the eigenvalues
![]() $ {\lambda}_2 $
and
$ {\lambda}_2 $
and
![]() $ {\lambda}_3 $
are not identical (Ding and Lew, Reference Ding and Lew2021; Zhou et al., Reference Zhou, Wu and Lew2024b). In these cases, one may consider a molecule wobbling uniformly within an elliptical cone of distinct angles of
$ {\lambda}_3 $
are not identical (Ding and Lew, Reference Ding and Lew2021; Zhou et al., Reference Zhou, Wu and Lew2024b). In these cases, one may consider a molecule wobbling uniformly within an elliptical cone of distinct angles of
![]() $ \alpha $
and
$ \alpha $
and
![]() $ \beta $
along the long and short axes, respectively. The eigenvalues (Eq. (35)) can be expressed as
$ \beta $
along the long and short axes, respectively. The eigenvalues (Eq. (35)) can be expressed as
 $$ {\lambda}_1=\frac{1}{3\Omega}{\int}_{\phi^{\prime }=0}^{2\pi }1-{t}^3\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime }, $$
$$ {\lambda}_1=\frac{1}{3\Omega}{\int}_{\phi^{\prime }=0}^{2\pi }1-{t}^3\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime }, $$
 $$ {\lambda}_2=\frac{1}{3\Omega}{\int}_{\phi^{\prime }=0}^{2\pi}\left({t}^3\left({\phi}^{\prime}\right)-3t\left({\phi}^{\prime}\right)+2\right){\sin}^2\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime }, $$
$$ {\lambda}_2=\frac{1}{3\Omega}{\int}_{\phi^{\prime }=0}^{2\pi}\left({t}^3\left({\phi}^{\prime}\right)-3t\left({\phi}^{\prime}\right)+2\right){\sin}^2\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime }, $$
 $$ {\lambda}_3=\frac{1}{3\Omega}{\int}_{\phi^{\prime }=0}^{2\pi}\left({t}^3\left({\phi}^{\prime}\right)-3t\left({\phi}^{\prime}\right)+2\right){\cos}^2\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime }, $$
$$ {\lambda}_3=\frac{1}{3\Omega}{\int}_{\phi^{\prime }=0}^{2\pi}\left({t}^3\left({\phi}^{\prime}\right)-3t\left({\phi}^{\prime}\right)+2\right){\cos}^2\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime }, $$
 $$ \Omega =2\pi -{\int}_{\phi^{\prime }=0}^{2\pi }t\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime },\hskip0.84em \mathrm{and} $$
$$ \Omega =2\pi -{\int}_{\phi^{\prime }=0}^{2\pi }t\left({\phi}^{\prime}\right)\mathrm{d}{\phi}^{\prime },\hskip0.84em \mathrm{and} $$
 $$ {\displaystyle \begin{array}{c}t\left(\phi^{\prime}\right)=\cos \left(\max \theta \left(\phi \right)\right)=\sqrt{1-\frac{\sin^2\left(\alpha \right)+{\sin}^2\left(\beta \right)}{\sin^2\left(\beta \right){\cos}^2\left(\phi \right)+{\sin}^2\left(\alpha \right){\sin}^2\left(\phi \right)}},\end{array}} $$
$$ {\displaystyle \begin{array}{c}t\left(\phi^{\prime}\right)=\cos \left(\max \theta \left(\phi \right)\right)=\sqrt{1-\frac{\sin^2\left(\alpha \right)+{\sin}^2\left(\beta \right)}{\sin^2\left(\beta \right){\cos}^2\left(\phi \right)+{\sin}^2\left(\alpha \right){\sin}^2\left(\phi \right)}},\end{array}} $$
where
![]() $ \max \theta \left(\phi \right) $
represents the boundary of the anisotropic wobble cone, rotated so that its center points along the
$ \max \theta \left(\phi \right) $
represents the boundary of the anisotropic wobble cone, rotated so that its center points along the
![]() $ {\mu}_z $
axis, parameterized by the maximum value of
$ {\mu}_z $
axis, parameterized by the maximum value of
![]() $ \theta $
as a function of
$ \theta $
as a function of
![]() $ \phi $
. The corresponding eigenvectors are given by
$ \phi $
. The corresponding eigenvectors are given by
 $$ {\boldsymbol{\nu}}_2=\left[\begin{array}{c}-\cos \theta \cos \phi \sin \psi -\sin \phi \cos \psi \\ {}-\cos \theta \sin \phi \sin \psi +\cos \phi \cos \psi \\ {}\sin \theta \sin \psi \end{array}\right]\hskip0.48em \mathrm{and} $$
$$ {\boldsymbol{\nu}}_2=\left[\begin{array}{c}-\cos \theta \cos \phi \sin \psi -\sin \phi \cos \psi \\ {}-\cos \theta \sin \phi \sin \psi +\cos \phi \cos \psi \\ {}\sin \theta \sin \psi \end{array}\right]\hskip0.48em \mathrm{and} $$
 $$ {\boldsymbol{\nu}}_3=\left[\begin{array}{c}\cos \theta \cos \phi \cos \psi -\sin \phi \sin \psi \\ {}\cos \theta \sin \phi \cos \psi -\cos \phi \sin \psi \\ {}-\sin \theta \cos \psi \end{array}\right]. $$
$$ {\boldsymbol{\nu}}_3=\left[\begin{array}{c}\cos \theta \cos \phi \cos \psi -\sin \phi \sin \psi \\ {}\cos \theta \sin \phi \cos \psi -\cos \phi \sin \psi \\ {}-\sin \theta \cos \psi \end{array}\right]. $$
One may model the anisotropy as having long and short axes oriented parallel and perpendicular to the optical axis (Figure 5e) or rotated by an arbitrary angle
![]() $ \psi $
(Figure 5f). Importantly, one may interpret the eigen decomposition of
$ \psi $
(Figure 5f). Importantly, one may interpret the eigen decomposition of
![]() $ \boldsymbol{M} $
as expressing
$ \boldsymbol{M} $
as expressing
![]() $ \boldsymbol{m} $
in a rotated coordinate system with
$ \boldsymbol{m} $
in a rotated coordinate system with
![]() $ {\mu}_z^{\prime } $
aligned with the dipole’s mean orientation and an equivalent second moment vector
$ {\mu}_z^{\prime } $
aligned with the dipole’s mean orientation and an equivalent second moment vector
![]() $ {\boldsymbol{m}}^{\prime }={\left[{\lambda}_3,{\lambda}_2,{\lambda}_1,0,0,0\right]}^{\top } $
. Therefore, the eigenvalues are simply equal to the first three squared second moments, each of which must be non-negative (Zhou et al., Reference Zhou, Wu and Lew2024b).
$ {\boldsymbol{m}}^{\prime }={\left[{\lambda}_3,{\lambda}_2,{\lambda}_1,0,0,0\right]}^{\top } $
. Therefore, the eigenvalues are simply equal to the first three squared second moments, each of which must be non-negative (Zhou et al., Reference Zhou, Wu and Lew2024b).
Alternatively, rotational dynamics can be expressed using generalized 3D Stokes parameters
![]() $ {s}_i $
, analogous to those used in standard polarimetry (Curcio et al., Reference Curcio, Alemán-Castañeda, Brown, Brasselet and Alonso2020). The relationship between the second moments and the Stokes parameters is given by
$ {s}_i $
, analogous to those used in standard polarimetry (Curcio et al., Reference Curcio, Alemán-Castañeda, Brown, Brasselet and Alonso2020). The relationship between the second moments and the Stokes parameters is given by
Note that
![]() $ {s}_3 $
,
$ {s}_3 $
,
![]() $ {s}_5 $
, and
$ {s}_5 $
, and
![]() $ {s}_7 $
are zero since we assume that the SMs have no chirality. We also note that spherical harmonics
$ {s}_7 $
are zero since we assume that the SMs have no chirality. We also note that spherical harmonics
![]() $ {Y}_l^m\left(\theta, \phi \right) $
may also be used as a basis to describe molecular rotational dynamics (Chandler et al., Reference Chandler, Shroff, Oldenbourg and Rivière2019b). These harmonics are convenient as a complete orthogonal basis for functions on a sphere, and they form the foundation of a unified framework for analyzing the image formation of individual dipoles and ensembles thereof (Chandler et al., Reference Chandler, Shroff, Oldenbourg and La Rivière2019a, Reference Chandler, Shroff, Oldenbourg and Rivière2019b, Reference Chandler, Shroff, Oldenbourg and La Rivière2020). Compared to fluorescence anisotropy, which projects orientation space into a single parameter, each of the aforementioned models provides a more detailed, high-dimensional description of SM rotational motions, and we recommend their use whenever possible.
$ {Y}_l^m\left(\theta, \phi \right) $
may also be used as a basis to describe molecular rotational dynamics (Chandler et al., Reference Chandler, Shroff, Oldenbourg and Rivière2019b). These harmonics are convenient as a complete orthogonal basis for functions on a sphere, and they form the foundation of a unified framework for analyzing the image formation of individual dipoles and ensembles thereof (Chandler et al., Reference Chandler, Shroff, Oldenbourg and La Rivière2019a, Reference Chandler, Shroff, Oldenbourg and Rivière2019b, Reference Chandler, Shroff, Oldenbourg and La Rivière2020). Compared to fluorescence anisotropy, which projects orientation space into a single parameter, each of the aforementioned models provides a more detailed, high-dimensional description of SM rotational motions, and we recommend their use whenever possible.
This analysis has key implications for the temporal resolution of SMOLM techniques. Since any fluorescence measurement involves collecting some number of photons over time, SMOLM wobble measurements, quantified via rotational constraint
![]() $ \gamma $
or angles
$ \gamma $
or angles
![]() $ {\alpha}_s $
,
$ {\alpha}_s $
,
![]() $ \alpha $
, and
$ \alpha $
, and
![]() $ \beta $
, therefore represent the degree of rotational diffusion that a molecule exhibits during the integration time. The choice of integration time typically balances several factors, including the duration of each fluorescence burst or fluorophore binding event, hardware limitations of the detector, and the desired angular precision of the measurement. Typical exposure times are 10 to 100 milliseconds for widefield imaging cameras (Table 1), which are useful for probing binding, phase separation, and aggregation dynamics (Nettels et al., Reference Nettels, Galvanetto, Ivanović, Nüesch, Yang and Schuler2024). Newly developed arrays of avalanche diodes have <200 ps precision (Bucci et al., Reference Bucci, Tortarolo, Held, Bega, Perego, Castagnetti, Bozzoni, Slenders and Vicidomini2024; Radmacher et al., Reference Radmacher, Nevskyi, Gallea, Thiele, Gregor, Rizzoli and Enderlein2024) for timing photon arrivals and can be adapted for SMOLM. Further, one may use SMOLM to track a molecule’s mean orientation
$ \beta $
, therefore represent the degree of rotational diffusion that a molecule exhibits during the integration time. The choice of integration time typically balances several factors, including the duration of each fluorescence burst or fluorophore binding event, hardware limitations of the detector, and the desired angular precision of the measurement. Typical exposure times are 10 to 100 milliseconds for widefield imaging cameras (Table 1), which are useful for probing binding, phase separation, and aggregation dynamics (Nettels et al., Reference Nettels, Galvanetto, Ivanović, Nüesch, Yang and Schuler2024). Newly developed arrays of avalanche diodes have <200 ps precision (Bucci et al., Reference Bucci, Tortarolo, Held, Bega, Perego, Castagnetti, Bozzoni, Slenders and Vicidomini2024; Radmacher et al., Reference Radmacher, Nevskyi, Gallea, Thiele, Gregor, Rizzoli and Enderlein2024) for timing photon arrivals and can be adapted for SMOLM. Further, one may use SMOLM to track a molecule’s mean orientation
![]() $ \boldsymbol{\mu} $
and wobble
$ \boldsymbol{\mu} $
and wobble
![]() $ \gamma $
, as well as its translational movements, over time, thereby enabling high-dimensional tracking of biomolecular dynamics.
$ \gamma $
, as well as its translational movements, over time, thereby enabling high-dimensional tracking of biomolecular dynamics.
Dipole-spread function engineering via modulating phase and polarization
The optical field at the image plane can be found by calculating the Fourier transform of the (modulated) field at the BFP (Figure 6d–f). Here, we denote any possible linear operation on the field at the BFP using a spatially varying Jones matrix
The image plane electric field for an in-focus emitter located at the origin (
![]() $ x=y={z}_{\mathrm{SM}}={z}_f=0 $
) is therefore given by
$ x=y={z}_{\mathrm{SM}}={z}_f=0 $
) is therefore given by
 $$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{img}}\left(\xi, \eta \right)=\mathcal{F}\left\{\boldsymbol{J}{\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu} \right\}=\mathcal{F}\left\{\boldsymbol{J}{\boldsymbol{G}}_{\mathrm{BFP}}\right\}\boldsymbol{\mu} ={\boldsymbol{G}}_{\mathrm{img}}\boldsymbol{\mu} \\ {}=\left[\begin{array}{ccc}{G}_x^{(x)}\left(\xi, \eta \right)& {G}_y^{(x)}\left(\xi, \eta \right)& {G}_z^{(x)}\left(\xi, \eta \right)\\ {}{G}_x^{(y)}\left(\xi, \eta \right)& {G}_y^{(y)}\left(\xi, \eta \right)& {G}_z^{(y)}\left(\xi, \eta \right)\\ {}0& 0& 0\end{array}\right]\boldsymbol{\mu}, \end{array}} $$
$$ {\displaystyle \begin{array}{c}{\boldsymbol{E}}_{\mathrm{img}}\left(\xi, \eta \right)=\mathcal{F}\left\{\boldsymbol{J}{\boldsymbol{G}}_{\mathrm{BFP}}\boldsymbol{\mu} \right\}=\mathcal{F}\left\{\boldsymbol{J}{\boldsymbol{G}}_{\mathrm{BFP}}\right\}\boldsymbol{\mu} ={\boldsymbol{G}}_{\mathrm{img}}\boldsymbol{\mu} \\ {}=\left[\begin{array}{ccc}{G}_x^{(x)}\left(\xi, \eta \right)& {G}_y^{(x)}\left(\xi, \eta \right)& {G}_z^{(x)}\left(\xi, \eta \right)\\ {}{G}_x^{(y)}\left(\xi, \eta \right)& {G}_y^{(y)}\left(\xi, \eta \right)& {G}_z^{(y)}\left(\xi, \eta \right)\\ {}0& 0& 0\end{array}\right]\boldsymbol{\mu}, \end{array}} $$
where
![]() $ \left(\xi, \eta \right) $
represents coordinates within the image plane and
$ \left(\xi, \eta \right) $
represents coordinates within the image plane and
![]() $ \mathcal{F}\left\{\cdotp \right\} $
represents a 2D Fourier transform performed by the tube lens [TL1 and TL2, Figure 7a]. Entries
$ \mathcal{F}\left\{\cdotp \right\} $
represents a 2D Fourier transform performed by the tube lens [TL1 and TL2, Figure 7a]. Entries
![]() $ {G}_i^{(j)} $
, with
$ {G}_i^{(j)} $
, with
![]() $ i,j\in \left\{x,y,z\right\} $
, are termed the basis fields at the image plane. Note that due to the Fourier transform,
$ i,j\in \left\{x,y,z\right\} $
, are termed the basis fields at the image plane. Note that due to the Fourier transform,
![]() $ {\boldsymbol{E}}_{\mathrm{img}} $
is shift-invariant with respect to the lateral position
$ {\boldsymbol{E}}_{\mathrm{img}} $
is shift-invariant with respect to the lateral position
![]() $ \left(x,y\right) $
of the molecule. However, the basis fields exhibit changes in their shapes when the molecule is defocused.
$ \left(x,y\right) $
of the molecule. However, the basis fields exhibit changes in their shapes when the molecule is defocused.

Figure 7. Representative images of recently developed and widely used dipole spread functions (DSFs). (a) Principle of a fluorescence microscope with polarized detection using a polarizing beamsplitter (PBS). An objective lens (OL) is placed at one focal length away from the dipole emitter. The tube lenses (TL1, TL2) perform optical Fourier transforms on the field at the back focal plane (BFP) modulated by an optical component represented by a
![]() $ 2\times 2 $
complex tensor
$ 2\times 2 $
complex tensor
![]() $ \boldsymbol{J}\left(u,v\right) $
and create the DSF at the detector plane. Images for molecules with various orientations and wobble using the (b) standard DSF (i) unpolarized and focused (Mortensen et al., Reference Mortensen, Churchman, Spudich and Flyvbjerg2010), (ii) polarized and focused (Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020), (iii) unpolarized and defocused (Böhmer and Enderlein, Reference Böhmer and Enderlein2003), (c) double-helix DSF, (d) multi-spot DSFs (i–iv) quadrated (Backer et al., Reference Backer, Backlund, Lew and Moerner2013), bisected (Backer et al., Reference Backer, Backlund, von Diezmann, Sahl and Moerner2014), tri-spot (Zhang et al., Reference Zhang, Lu, Ding and Lew2018), duo-spot (Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020 DSFs), (e) vortex DSF (Ding and Lew, Reference Ding and Lew2021; Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021), (f) radially and azimuthally polarized (raPol) standard DSF (Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022), (g) pixOL (Wu et al., Reference Wu, Lu and Lew2022a), and (h) CHIDO (Curcio et al., Reference Curcio, Alemán-Castañeda, Brown, Brasselet and Alonso2020). (j) Images from eight channels of the multi-view-reflector (MVR) microscope (Zhang et al., Reference Zhang, Guo, He, Wu, Vahey and Lew2023). Molecule with (1)
$ \boldsymbol{J}\left(u,v\right) $
and create the DSF at the detector plane. Images for molecules with various orientations and wobble using the (b) standard DSF (i) unpolarized and focused (Mortensen et al., Reference Mortensen, Churchman, Spudich and Flyvbjerg2010), (ii) polarized and focused (Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020), (iii) unpolarized and defocused (Böhmer and Enderlein, Reference Böhmer and Enderlein2003), (c) double-helix DSF, (d) multi-spot DSFs (i–iv) quadrated (Backer et al., Reference Backer, Backlund, Lew and Moerner2013), bisected (Backer et al., Reference Backer, Backlund, von Diezmann, Sahl and Moerner2014), tri-spot (Zhang et al., Reference Zhang, Lu, Ding and Lew2018), duo-spot (Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020 DSFs), (e) vortex DSF (Ding and Lew, Reference Ding and Lew2021; Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021), (f) radially and azimuthally polarized (raPol) standard DSF (Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022), (g) pixOL (Wu et al., Reference Wu, Lu and Lew2022a), and (h) CHIDO (Curcio et al., Reference Curcio, Alemán-Castañeda, Brown, Brasselet and Alonso2020). (j) Images from eight channels of the multi-view-reflector (MVR) microscope (Zhang et al., Reference Zhang, Guo, He, Wu, Vahey and Lew2023). Molecule with (1)
![]() $ \left[\theta, \phi \right]=\left[{90}^{\circ },{0}^{\circ}\right] $
, (2)
$ \left[\theta, \phi \right]=\left[{90}^{\circ },{0}^{\circ}\right] $
, (2)
![]() $ \left[\theta, \phi \right]=\left[{90}^{\circ },{90}^{\circ}\right] $
, (3)
$ \left[\theta, \phi \right]=\left[{90}^{\circ },{90}^{\circ}\right] $
, (3)
![]() $ \theta ={0}^{\circ } $
, and (4)
$ \theta ={0}^{\circ } $
, and (4)
![]() $ \left[\theta, \phi \right]=\left[{45}^{\circ },{0}^{\circ}\right] $
. (5) Isotropic emitter. Purple: in-focus molecules; green: molecules defocused by (b) 500 nm and (c–h) 200 nm. Color bar: normalized intensity; scale bar: 500 nm.
$ \left[\theta, \phi \right]=\left[{45}^{\circ },{0}^{\circ}\right] $
. (5) Isotropic emitter. Purple: in-focus molecules; green: molecules defocused by (b) 500 nm and (c–h) 200 nm. Color bar: normalized intensity; scale bar: 500 nm.
Similar to Eqs. (14) and (34), the forward imaging model using emission modulation can be written as
 $$ {\displaystyle \begin{array}{c}\boldsymbol{I}=\left[\begin{array}{c}{I}^{(x)}\\ {}{I}^{(y)}\end{array}\right]=s\left[\begin{array}{cc}\begin{array}{ccc}{B}_{xx}^{(x)}& {B}_{yy}^{(x)}& {B}_{zz}^{(x)}\\ {}{B}_{xx}^{(y)}& {B}_{yy}^{(y)}& {B}_{zz}^{(y)}\end{array}& \begin{array}{ccc}{B}_{xy}^{(x)}& {B}_{xz}^{(x)}& {B}_{yz}^{(x)}\\ {}{B}_{xy}^{(y)}& {B}_{xz}^{(y)}& {B}_{yz}^{(y)}\end{array}\end{array}\right]\boldsymbol{m}=s\boldsymbol{Bm}\\ {}=s\left[\begin{array}{cc}\begin{array}{ccc}{\left|{G}_x^{(x)}\right|}^2& {\left|{G}_y^{(x)}\right|}^2& {\left|{G}_z^{(x)}\right|}^2\\ {}{\left|{G}_x^{(y)}\right|}^2& {\left|{G}_y^{(y)}\right|}^2& {\left|{G}_z^{(y)}\right|}^2\end{array}& \begin{array}{ccc}2\operatorname{Re}\left\{{G}_x^{(x)\ast }{G}_y^{(x)}\right\}& 2\operatorname{Re}\left\{{G}_x^{(x)\ast }{G}_z^{(x)}\right\}& 2\operatorname{Re}\left\{{G}_y^{(x)\ast }{G}_z^{(x)}\right\}\\ {}2\operatorname{Re}\left\{{G}_x^{(y)\ast }{G}_y^{(y)}\right\}& 2\operatorname{Re}\left\{{G}_x^{(y)\ast }{G}_z^{(y)}\right\}& 2\operatorname{Re}\left\{{G}_y^{(y)\ast }{G}_z^{(y)}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{m}_{xx}\\ {}{m}_{yy}\\ {}{m}_{zz}\end{array}\\ {}\begin{array}{c}{m}_{xy}\\ {}{m}_{xz}\\ {}{m}_{yz}\end{array}\end{array}\right],\end{array}} $$
$$ {\displaystyle \begin{array}{c}\boldsymbol{I}=\left[\begin{array}{c}{I}^{(x)}\\ {}{I}^{(y)}\end{array}\right]=s\left[\begin{array}{cc}\begin{array}{ccc}{B}_{xx}^{(x)}& {B}_{yy}^{(x)}& {B}_{zz}^{(x)}\\ {}{B}_{xx}^{(y)}& {B}_{yy}^{(y)}& {B}_{zz}^{(y)}\end{array}& \begin{array}{ccc}{B}_{xy}^{(x)}& {B}_{xz}^{(x)}& {B}_{yz}^{(x)}\\ {}{B}_{xy}^{(y)}& {B}_{xz}^{(y)}& {B}_{yz}^{(y)}\end{array}\end{array}\right]\boldsymbol{m}=s\boldsymbol{Bm}\\ {}=s\left[\begin{array}{cc}\begin{array}{ccc}{\left|{G}_x^{(x)}\right|}^2& {\left|{G}_y^{(x)}\right|}^2& {\left|{G}_z^{(x)}\right|}^2\\ {}{\left|{G}_x^{(y)}\right|}^2& {\left|{G}_y^{(y)}\right|}^2& {\left|{G}_z^{(y)}\right|}^2\end{array}& \begin{array}{ccc}2\operatorname{Re}\left\{{G}_x^{(x)\ast }{G}_y^{(x)}\right\}& 2\operatorname{Re}\left\{{G}_x^{(x)\ast }{G}_z^{(x)}\right\}& 2\operatorname{Re}\left\{{G}_y^{(x)\ast }{G}_z^{(x)}\right\}\\ {}2\operatorname{Re}\left\{{G}_x^{(y)\ast }{G}_y^{(y)}\right\}& 2\operatorname{Re}\left\{{G}_x^{(y)\ast }{G}_z^{(y)}\right\}& 2\operatorname{Re}\left\{{G}_y^{(y)\ast }{G}_z^{(y)}\right\}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{m}_{xx}\\ {}{m}_{yy}\\ {}{m}_{zz}\end{array}\\ {}\begin{array}{c}{m}_{xy}\\ {}{m}_{xz}\\ {}{m}_{yz}\end{array}\end{array}\right],\end{array}} $$
where
![]() $ {B}_{ij}^{(k)} $
, with
$ {B}_{ij}^{(k)} $
, with
![]() $ i,j\in \left\{x,y,z\right\} $
and
$ i,j\in \left\{x,y,z\right\} $
and
![]() $ k\in \left\{x,y\right\} $
, are termed the
$ k\in \left\{x,y\right\} $
, are termed the
![]() $ k $
-polarized basis images describing the response (dipole spread function, DSF) of the imaging system to a dipole emitter. For unpolarized detection, the detected image is given by
$ k $
-polarized basis images describing the response (dipole spread function, DSF) of the imaging system to a dipole emitter. For unpolarized detection, the detected image is given by
![]() $ {I}^{(x)}+{I}^{(y)} $
, a mixture of both polarized images. We can also resolve
$ {I}^{(x)}+{I}^{(y)} $
, a mixture of both polarized images. We can also resolve
![]() $ {I}^{(x)} $
and
$ {I}^{(x)} $
and
![]() $ {I}^{(y)} $
separately by placing a PBS in the emission path (Figure 7a).
$ {I}^{(y)} $
separately by placing a PBS in the emission path (Figure 7a).
For an unpolarized conventional microscope without additional modulation at the BFP, i.e.,
![]() $ {J}_{11}\left(u,v\right)={J}_{22}\left(u,v\right)=1 $
and
$ {J}_{11}\left(u,v\right)={J}_{22}\left(u,v\right)=1 $
and
![]() $ {J}_{12}\left(u,v\right)={J}_{21}\left(u,v\right)=0 $
, SM orientation can be measured by fitting the shape of the measured images to the theoretical model [Figure 7b(i)] (Mortensen et al., Reference Mortensen, Churchman, Spudich and Flyvbjerg2010); the image corresponding to an in-(
$ {J}_{12}\left(u,v\right)={J}_{21}\left(u,v\right)=0 $
, SM orientation can be measured by fitting the shape of the measured images to the theoretical model [Figure 7b(i)] (Mortensen et al., Reference Mortensen, Churchman, Spudich and Flyvbjerg2010); the image corresponding to an in-(
![]() $ xy $
) plane molecule exhibits an elliptical shape with an elongation direction parallel to the molecular orientation [Figure 7b(i)(1,2)] while the image corresponding to a
$ xy $
) plane molecule exhibits an elliptical shape with an elongation direction parallel to the molecular orientation [Figure 7b(i)(1,2)] while the image corresponding to a
![]() $ z $
-oriented molecule exhibits a donut shape [Figure 7b(i)(3)]. One can also separate the
$ z $
-oriented molecule exhibits a donut shape [Figure 7b(i)(3)]. One can also separate the
![]() $ x $
- and
$ x $
- and
![]() $ y $
-polarized emission light to obtain more distinct basis images for x- and y-oriented molecules [Figure 7b(ii)(1,2)]. This polarization-resolved DSF was used to resolve the structural heterogeneity within amyloid aggregates (Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020). Both the unpolarized and polarized standard DSFs are typically implemented to image molecules located close to the air-glass or water–glass interface because the additional phase caused by refractive index mismatch further improves orientational sensitivity by breaking the symmetry in the basis fields (Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020; Zhang and Lew, Reference Zhang and Lew2021b). The standard DSF can also be implemented with a defocus of ~500 nm to 1 μm (Böhmer and Enderlein, Reference Böhmer and Enderlein2003). While localization precision is reduced as the photons are spread across a larger area, the more distinct images [Figure 7b(iii)] significantly improve orientational sensitivity. Defocused imaging has been used for imaging rotations of SMs embedded within polymers (Dickson et al., Reference Dickson, Norris and Moerner1998; Patra et al., Reference Patra, Gregor and Enderlein2004; Uji-i et al., Reference Uji-i, Melnikov, Deres, Bergamini, De Schryver, Herrmann, Müllen, Enderlein and Hofkens2006) and resolving the stepping of Myosin V motors (Toprak et al., Reference Toprak, Enderlein, Syed, McKinney, Petschek, Ha, Goldman and Selvin2006).
$ y $
-polarized emission light to obtain more distinct basis images for x- and y-oriented molecules [Figure 7b(ii)(1,2)]. This polarization-resolved DSF was used to resolve the structural heterogeneity within amyloid aggregates (Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020). Both the unpolarized and polarized standard DSFs are typically implemented to image molecules located close to the air-glass or water–glass interface because the additional phase caused by refractive index mismatch further improves orientational sensitivity by breaking the symmetry in the basis fields (Ding et al., Reference Ding, Wu, Mazidi, Zhang and Lew2020; Zhang and Lew, Reference Zhang and Lew2021b). The standard DSF can also be implemented with a defocus of ~500 nm to 1 μm (Böhmer and Enderlein, Reference Böhmer and Enderlein2003). While localization precision is reduced as the photons are spread across a larger area, the more distinct images [Figure 7b(iii)] significantly improve orientational sensitivity. Defocused imaging has been used for imaging rotations of SMs embedded within polymers (Dickson et al., Reference Dickson, Norris and Moerner1998; Patra et al., Reference Patra, Gregor and Enderlein2004; Uji-i et al., Reference Uji-i, Melnikov, Deres, Bergamini, De Schryver, Herrmann, Müllen, Enderlein and Hofkens2006) and resolving the stepping of Myosin V motors (Toprak et al., Reference Toprak, Enderlein, Syed, McKinney, Petschek, Ha, Goldman and Selvin2006).
Engineering phase masks
Since the early 1980s (Cathey et al., Reference Cathey, Frieden, Rhodes and Rushforth1984; Dowski and Cathey, Reference Dowski and Cathey1995; Ojeda-Castañeda et al., Reference Ojeda-Castañeda, Andrés and Díaz1986), point-spread function (PSF) engineering has been explored to extend the capabilities of conventional microscopes. In the case of SMOLM, by manipulating the optical field at the BFP using a spatially varying Jones matrix
![]() $ \boldsymbol{J}\left(u,v\right) $
, one can improve the orientational sensitivity of the microscope and make more accurate and precise measurements. Experimentally, engineered DSFs are often implemented by adding a 4f system to the detection path of a fluorescence microscope that facilitates easy access to the BFP. Many DSFs, e.g., the double-helix (DH) DSF (Pavani and Piestun, Reference Pavani and Piestun2008; Pavani et al., Reference Pavani, Thompson, Biteen, Liu, Twieg, Piestun and Moerner2009; Backlund et al., Reference Backlund, Lew, Backer, Sahl, Grover, Agrawal, Piestun and Moerner2012), multi-spot DSFs (Backer et al., Reference Backer, Backlund, Lew and Moerner2013, Reference Backer, Backlund, von Diezmann, Sahl and Moerner2014; Zhang et al., Reference Zhang, Lu, Ding and Lew2018; Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020), vortex DSFs (Ding and Lew, Reference Ding and Lew2021; Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021), and pixel-wise optimized DSF (Wu et al., Reference Wu, Lu and Lew2022a) engineered for measuring 3D orientation and localization (pixOL), are designed using phase-only modulation, i.e.,
$ \boldsymbol{J}\left(u,v\right) $
, one can improve the orientational sensitivity of the microscope and make more accurate and precise measurements. Experimentally, engineered DSFs are often implemented by adding a 4f system to the detection path of a fluorescence microscope that facilitates easy access to the BFP. Many DSFs, e.g., the double-helix (DH) DSF (Pavani and Piestun, Reference Pavani and Piestun2008; Pavani et al., Reference Pavani, Thompson, Biteen, Liu, Twieg, Piestun and Moerner2009; Backlund et al., Reference Backlund, Lew, Backer, Sahl, Grover, Agrawal, Piestun and Moerner2012), multi-spot DSFs (Backer et al., Reference Backer, Backlund, Lew and Moerner2013, Reference Backer, Backlund, von Diezmann, Sahl and Moerner2014; Zhang et al., Reference Zhang, Lu, Ding and Lew2018; Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020), vortex DSFs (Ding and Lew, Reference Ding and Lew2021; Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021), and pixel-wise optimized DSF (Wu et al., Reference Wu, Lu and Lew2022a) engineered for measuring 3D orientation and localization (pixOL), are designed using phase-only modulation, i.e.,
where
![]() $ {\psi}_x\left(u,v\right) $
and
$ {\psi}_x\left(u,v\right) $
and
![]() $ {\psi}_y\left(u,v\right) $
are the additional phase masks added to the
$ {\psi}_y\left(u,v\right) $
are the additional phase masks added to the
![]() $ x $
and
$ x $
and
![]() $ y $
-polarized BFP, respectively. These DSFs can be implemented using a single spatial light modulator in a 4f system (Figure 8a,b), as shown in (Backlund et al., Reference Backlund, Lew, Backer, Sahl, Grover, Agrawal, Piestun and Moerner2012; Backer et al., Reference Backer, Backlund, von Diezmann, Sahl and Moerner2014; Zhang et al., Reference Zhang, Lu, Ding and Lew2018). In this configuration, the phase masks
$ y $
-polarized BFP, respectively. These DSFs can be implemented using a single spatial light modulator in a 4f system (Figure 8a,b), as shown in (Backlund et al., Reference Backlund, Lew, Backer, Sahl, Grover, Agrawal, Piestun and Moerner2012; Backer et al., Reference Backer, Backlund, von Diezmann, Sahl and Moerner2014; Zhang et al., Reference Zhang, Lu, Ding and Lew2018). In this configuration, the phase masks
![]() $ {\psi}_x\left(u,v\right) $
and
$ {\psi}_x\left(u,v\right) $
and
![]() $ {\psi}_y\left(u,v\right) $
may simply be rotated versions of each other.
$ {\psi}_y\left(u,v\right) $
may simply be rotated versions of each other.

Figure 8. (a, b) Schematic of a polarization-sensitive 4f imaging system appended to the detection path of a fluorescence microscope for modulating the phase at the back focal plane (BFP) using a spatial light modulator (SLM). (a) After separating the
![]() $ x $
(red) and
$ x $
(red) and
![]() $ y $
(blue) polarized fluorescence using a polarizing beamsplitter (PBS), light is guided towards a pyramid mirror and (b) reflected upwards towards the SLM. Both
$ y $
(blue) polarized fluorescence using a polarizing beamsplitter (PBS), light is guided towards a pyramid mirror and (b) reflected upwards towards the SLM. Both
![]() $ x $
and
$ x $
and
![]() $ y $
-polarized BFP are positioned at the same area on the SLM. Arrows on the phase mask represent the light polarization on the SLM. Both imaging channels are collected using camera C1. (c) Schematic of the raMVR microscope. After turning radially and azimuthally polarized fluorescence to
$ y $
-polarized BFP are positioned at the same area on the SLM. Arrows on the phase mask represent the light polarization on the SLM. Both imaging channels are collected using camera C1. (c) Schematic of the raMVR microscope. After turning radially and azimuthally polarized fluorescence to
![]() $ x $
- and
$ x $
- and
![]() $ y $
-polarized light using a variable wave plate (VaWP) and a vortex wave plate (VWP), a PBS and two sets of pyramid mirrors separate lights into eight detection channels, captured by cameras C1 and C2.
$ y $
-polarized light using a variable wave plate (VaWP) and a vortex wave plate (VWP), a PBS and two sets of pyramid mirrors separate lights into eight detection channels, captured by cameras C1 and C2.
The double-helix (DH) DSF was originally designed for measuring the axial position
![]() $ {z}_{\mathrm{SM}} $
of SMs (Pavani and Piestun, Reference Pavani and Piestun2008; Pavani et al., Reference Pavani, Thompson, Biteen, Liu, Twieg, Piestun and Moerner2009); the image of a single emitter exhibits two lobes revolving around each other as a function of
$ {z}_{\mathrm{SM}} $
of SMs (Pavani and Piestun, Reference Pavani and Piestun2008; Pavani et al., Reference Pavani, Thompson, Biteen, Liu, Twieg, Piestun and Moerner2009); the image of a single emitter exhibits two lobes revolving around each other as a function of
![]() $ {z}_{\mathrm{SM}} $
. It may be implemented using an SLM or by placing a commercially available transmissive phase plate (Gahlmann et al., Reference Gahlmann, Ptacin, Grover, Quirin, von Diezmann, Lee, Backlund, Shapiro, Piestun and Moerner2013) in the BFP of an imaging system. The orientation information is encoded in the relative brightness of the lobes (Backlund et al., Reference Backlund, Lew, Backer, Sahl, Grover, Agrawal, Piestun and Moerner2012). For example, in the
$ {z}_{\mathrm{SM}} $
. It may be implemented using an SLM or by placing a commercially available transmissive phase plate (Gahlmann et al., Reference Gahlmann, Ptacin, Grover, Quirin, von Diezmann, Lee, Backlund, Shapiro, Piestun and Moerner2013) in the BFP of an imaging system. The orientation information is encoded in the relative brightness of the lobes (Backlund et al., Reference Backlund, Lew, Backer, Sahl, Grover, Agrawal, Piestun and Moerner2012). For example, in the
![]() $ x $
-polarized imaging channel, one lobe is significantly brighter compared to the other if the molecule is tilted within the
$ x $
-polarized imaging channel, one lobe is significantly brighter compared to the other if the molecule is tilted within the
![]() $ xz $
-plane by ~
$ xz $
-plane by ~
![]() $ {45}^{\circ } $
[Figure 7c(4)]. In their work, the authors note that by simultaneously estimating the position and orientation of SMs using the DH DSF, orientation-induced systematic localization errors (Engelhardt et al., Reference Engelhardt, Keller, Hoyer, Reuss, Staudt and Hell2011) may be greatly improved; the experimental standard deviation averaged over a 2 μm depth range is reduced from 116 nm to 34 nm with 5925 signal photons and 9 background photons per pixel detected. One limitation of the DH DSF is that the image of z-oriented molecules is difficult to distinguish from those of isotropic emitters [Figure 7c(3,5)]. Consequently, the authors note that their localization correction works best for intermediately inclined molecules, i.e.,
$ {45}^{\circ } $
[Figure 7c(4)]. In their work, the authors note that by simultaneously estimating the position and orientation of SMs using the DH DSF, orientation-induced systematic localization errors (Engelhardt et al., Reference Engelhardt, Keller, Hoyer, Reuss, Staudt and Hell2011) may be greatly improved; the experimental standard deviation averaged over a 2 μm depth range is reduced from 116 nm to 34 nm with 5925 signal photons and 9 background photons per pixel detected. One limitation of the DH DSF is that the image of z-oriented molecules is difficult to distinguish from those of isotropic emitters [Figure 7c(3,5)]. Consequently, the authors note that their localization correction works best for intermediately inclined molecules, i.e.,
![]() $ \theta \in \left[{35}^{\circ },{75}^{\circ}\right] $
.
$ \theta \in \left[{35}^{\circ },{75}^{\circ}\right] $
.
The design of another family of DSFs, the multi-spot DSFs, leverages the fact that the intensity distribution at the BFP changes as a function of molecular orientation (Figure 7d). These techniques segment the BFP into multiple sections, and various linear phase ramps are placed in these sections. Since the Fourier transform of a linear phase gradient is a lateral shift of the kernel, the additional phase creates a multi-spot DSF at the image plane, where each spot exhibits a lateral shift depending on the phase ramp in the corresponding area at the BFP. Intuitively, orientation information is encoded in the relative brightness between the spots, similar to the DH DSF.
Two early methods, the quadrated [Figure 7d(i)] (Backer et al., Reference Backer, Backlund, Lew and Moerner2013) and bisected [Figure 7d(ii)] (Backer et al., Reference Backer, Backlund, von Diezmann, Sahl and Moerner2014) DSFs, both use a symmetric partitioning strategy. The quadrated DSF imaged dicyanomethylenedihydrofuran-N-6 (DCDHF-N-6) molecules embedded within polymethyl methacrylate (PMMA) with orientation precisions of
![]() $ {\sigma}_{\theta }={1.8}^{\circ } $
and
$ {\sigma}_{\theta }={1.8}^{\circ } $
and
![]() $ {\sigma}_{\phi }={1.7}^{\circ } $
and 2370 photons detected. The bisected DSF is resolved by the 3D position and orientation of SMs attached to microtubules in a BSC-1 cell within an axial range of 500 nm. Similar to the DH DSF, the bisected DSF can also remove orientation-induced localization errors and resolve the axial position
$ {\sigma}_{\phi }={1.7}^{\circ } $
and 2370 photons detected. The bisected DSF is resolved by the 3D position and orientation of SMs attached to microtubules in a BSC-1 cell within an axial range of 500 nm. Similar to the DH DSF, the bisected DSF can also remove orientation-induced localization errors and resolve the axial position
![]() $ z $
of an SM using the relative positions of its spots. However, both the quadrated and bisected DSFs exhibit an orientational degeneracy when distinguishing between z-oriented molecules versus isotropic emitters. The tri-spot DSF [Figure 7d(iii)] (Zhang et al., Reference Zhang, Lu, Ding and Lew2018) was later developed to eliminate the degeneracy by creating six linearly independent basis images; i.e., six spots within the image plane are used to estimate all six second-order orientational moments
$ z $
of an SM using the relative positions of its spots. However, both the quadrated and bisected DSFs exhibit an orientational degeneracy when distinguishing between z-oriented molecules versus isotropic emitters. The tri-spot DSF [Figure 7d(iii)] (Zhang et al., Reference Zhang, Lu, Ding and Lew2018) was later developed to eliminate the degeneracy by creating six linearly independent basis images; i.e., six spots within the image plane are used to estimate all six second-order orientational moments
![]() $ \boldsymbol{m} $
. Therefore, it can measure not only the orientation but also the rotational “wobble” of a molecule within a cone of solid angle
$ \boldsymbol{m} $
. Therefore, it can measure not only the orientation but also the rotational “wobble” of a molecule within a cone of solid angle
![]() $ \Omega $
during a camera frame (see Modeling the rotational diffusion of fluorescent molecules for details). It was used to resolve anisotropic emission from fluorescent beads and SMs embedded within polymers, as well as SM orientation and wobble dynamics within supported lipid membranes (Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020). Precisions of
$ \Omega $
during a camera frame (see Modeling the rotational diffusion of fluorescent molecules for details). It was used to resolve anisotropic emission from fluorescent beads and SMs embedded within polymers, as well as SM orientation and wobble dynamics within supported lipid membranes (Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020). Precisions of
![]() $ {\sigma}_{\theta }={6.0}^{\circ } $
and
$ {\sigma}_{\theta }={6.0}^{\circ } $
and
![]() $ {\sigma}_{\phi }={10.6}^{\circ } $
for measuring orientation and
$ {\sigma}_{\phi }={10.6}^{\circ } $
for measuring orientation and
![]() $ {\sigma}_{\Omega}=0.11\pi $
sr for measuring the wobble cone angle were reported for 1300 signal photons and 5 background photons per pixel detected. The duo-spot DSF [Figure 7d(iv)] (Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020) was also designed based on the intensity distribution at the BFP specifically for distinguishing in-plane molecules from
$ {\sigma}_{\Omega}=0.11\pi $
sr for measuring the wobble cone angle were reported for 1300 signal photons and 5 background photons per pixel detected. The duo-spot DSF [Figure 7d(iv)] (Lu et al., Reference Lu, Mazidi, Ding, Zhang and Lew2020) was also designed based on the intensity distribution at the BFP specifically for distinguishing in-plane molecules from
![]() $ z $
-oriented molecules. For in-plane molecules, two spots with similar brightness were observed in each polarization channel [Figure 7d(iv)(1,2)]; for z-oriented molecules, only one spot in each channel will be detected [Figure 7d(iv)(3)]. It was also used in lipid membrane imaging, yielding precisions of
$ z $
-oriented molecules. For in-plane molecules, two spots with similar brightness were observed in each polarization channel [Figure 7d(iv)(1,2)]; for z-oriented molecules, only one spot in each channel will be detected [Figure 7d(iv)(3)]. It was also used in lipid membrane imaging, yielding precisions of
![]() $ {\sigma}_{\theta }={8.4}^{\circ } $
,
$ {\sigma}_{\theta }={8.4}^{\circ } $
,
![]() $ {\sigma}_{\phi }={21.8}^{\circ } $
, and
$ {\sigma}_{\phi }={21.8}^{\circ } $
, and
![]() $ {\sigma}_{\Omega}=0.16\pi $
sr with 950 signal photons and 5 background photons per pixel detected.
$ {\sigma}_{\Omega}=0.16\pi $
sr with 950 signal photons and 5 background photons per pixel detected.
The vortex DSF is implemented by adding a vortex phase plate, which is usually used in STED microscopy to create a donut-shaped depletion laser pattern, to the emission path. The features of this DSF are opposite of those of the standard DSF (Figure 7b); images corresponding to in-plane molecules exhibit a donut shape [Figure 7e(1)], whereas images corresponding to
![]() $ z $
-oriented molecules are single-focused spots [Figure 7e(3)]. The orientational measurement precisions of both the unpolarized [Figure 7e(i)] (Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021) and (
$ z $
-oriented molecules are single-focused spots [Figure 7e(3)]. The orientational measurement precisions of both the unpolarized [Figure 7e(i)] (Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021) and (
![]() $ x $
and
$ x $
and
![]() $ y $
) polarized [Figure 7e(ii)] (Ding and Lew Reference Ding and Lew2021) vortex DSFs are superior to those of the analogous standard DSFs. The unpolarized vortex DSF was used to resolve different periodicities of plectoneme structures where two helices intertwine with each other within supercoiled DNA. Imaging λ-DNA on a tilted coverslip, it achieved an orientation precision of
$ y $
) polarized [Figure 7e(ii)] (Ding and Lew Reference Ding and Lew2021) vortex DSFs are superior to those of the analogous standard DSFs. The unpolarized vortex DSF was used to resolve different periodicities of plectoneme structures where two helices intertwine with each other within supercoiled DNA. Imaging λ-DNA on a tilted coverslip, it achieved an orientation precision of
![]() $ {\sigma}_{\theta }={3.1}^{\circ } $
,
$ {\sigma}_{\theta }={3.1}^{\circ } $
,
![]() $ {\sigma}_{\phi }={5.5}^{\circ } $
, and a wobble precision of
$ {\sigma}_{\phi }={5.5}^{\circ } $
, and a wobble precision of
![]() $ {\sigma}_{\Omega}=0.37 $
sr (converted from the published measurements), as well as localization precisions of
$ {\sigma}_{\Omega}=0.37 $
sr (converted from the published measurements), as well as localization precisions of
![]() $ {\sigma}_{xy}=5.6 $
nm along the lateral direction and
$ {\sigma}_{xy}=5.6 $
nm along the lateral direction and
![]() $ {\sigma}_z=27 $
nm along the axial direction with 4000 signal photons and 10 background photons/pixel detected (Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021). The polarized vortex DSF achieves orientation precisions of
$ {\sigma}_z=27 $
nm along the axial direction with 4000 signal photons and 10 background photons/pixel detected (Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021). The polarized vortex DSF achieves orientation precisions of
![]() $ {\sigma}_{\theta }={4.5}^{\circ } $
and
$ {\sigma}_{\theta }={4.5}^{\circ } $
and
![]() $ {\sigma}_{\phi }={7.7}^{\circ } $
and a lateral localization precision of
$ {\sigma}_{\phi }={7.7}^{\circ } $
and a lateral localization precision of
![]() $ {\sigma}_{xy}=12.5 $
nm with 510 signal photons and 2.3 background photons/pixel detected. Further, the authors show that this DSF is capable of resolving anisotropic wobbling, i.e., a molecule that diffuses rotationally within an elliptical cone (Zhou et al., Reference Zhou, Wu and Lew2024b), within a single camera frame (see Modeling the rotational diffusion of fluorescent molecules for details). They find that NR molecules bound within DPPC SLBs tend to wobble along the direction parallel to acyl chains; whereas those bound to Aβ42 oligomers exhibit a wide distribution for wobble anisotropy.
$ {\sigma}_{xy}=12.5 $
nm with 510 signal photons and 2.3 background photons/pixel detected. Further, the authors show that this DSF is capable of resolving anisotropic wobbling, i.e., a molecule that diffuses rotationally within an elliptical cone (Zhou et al., Reference Zhou, Wu and Lew2024b), within a single camera frame (see Modeling the rotational diffusion of fluorescent molecules for details). They find that NR molecules bound within DPPC SLBs tend to wobble along the direction parallel to acyl chains; whereas those bound to Aβ42 oligomers exhibit a wide distribution for wobble anisotropy.
Another phase mask was designed by numerical optimization, i.e., maximizing the Fisher information (Moon and Stirling, Reference Moon and Stirling2000) of measuring the orientational second moments, similar to that used to create the tetrapod DSF (Shechtman et al., Reference Shechtman, Weiss, Backer, Sahl and Moerner2015) for 3D SMLM. This method, termed pixel-wise DSF engineering for measuring the 3D orientation and localization (pixOL) (Wu et al., Reference Wu, Lu and Lew2022a), produced a phase mask with a smaller phase gradient compared to other engineered phase masks. The basis images exhibit similar features to those of the
![]() $ x $
and
$ x $
and
![]() $ y $
-polarized (
$ y $
-polarized (
![]() $ xy $
Pol) standard DSF when in focus (Figure 7g, purple). However, it breaks the defocus symmetry of the standard DSF and is more suitable for 3D imaging (Figure 7g, green). Over a 700 nm depth range, the pixOL DSF achieves an orientation precision of
$ xy $
Pol) standard DSF when in focus (Figure 7g, purple). However, it breaks the defocus symmetry of the standard DSF and is more suitable for 3D imaging (Figure 7g, green). Over a 700 nm depth range, the pixOL DSF achieves an orientation precision of
![]() $ {\sigma}_{\boldsymbol{\mu}}={4.1}^{\circ } $
(an arc length on the orientation unit sphere, i.e., a geometric average between
$ {\sigma}_{\boldsymbol{\mu}}={4.1}^{\circ } $
(an arc length on the orientation unit sphere, i.e., a geometric average between
![]() $ {\sigma}_{\theta } $
and
$ {\sigma}_{\theta } $
and
![]() $ {\sigma}_{\phi } $
that accounts for their correlation), a wobble precision of
$ {\sigma}_{\phi } $
that accounts for their correlation), a wobble precision of
![]() $ {\sigma}_{\Omega}=0.44 $
sr, and localization precisions of
$ {\sigma}_{\Omega}=0.44 $
sr, and localization precisions of
![]() $ {\sigma}_{xy}=23.2 $
nm along the lateral direction and
$ {\sigma}_{xy}=23.2 $
nm along the lateral direction and
![]() $ {\sigma}_z=19.5 $
nm with 2500 signal photons and 3 background photons/pixel detected. As a proof of principle, the authors demonstrate this DSF by imaging NR molecules bound within a spherical SLB consisting of DPPC and 40% cholesterol. The pixOL measurements showed that NR molecules are highly constrained to an orientation perpendicular to the membrane—an ideal calibration target for 3D SMOLM.
$ {\sigma}_z=19.5 $
nm with 2500 signal photons and 3 background photons/pixel detected. As a proof of principle, the authors demonstrate this DSF by imaging NR molecules bound within a spherical SLB consisting of DPPC and 40% cholesterol. The pixOL measurements showed that NR molecules are highly constrained to an orientation perpendicular to the membrane—an ideal calibration target for 3D SMOLM.
Beyond classical optimization, machine learning can also be used for phase mask design in a manner similar to technologies developed for 3D SMLM (Nehme et al., Reference Nehme, Freedman, Gordon, Ferdman, Weiss, Alalouf, Naor, Orange, Michaeli and Shechtman2020). Here, the goal is to use deep learning to explore the high dimensional design space robustly and construct a phase mask that is optimal for a specific measurement task; i.e., the optimized design achieves a minimized error rate. Jointly minimizing the error of measuring 3D position and 3D orientation, Jouchet et al. used this technique to produce the Arrowhead phase mask (Jouchet et al., Reference Jouchet, Roy and Moerner2023). Imaging single DCDHF-N-6 molecules within PMMA, the arrowhead mask achieves experimental precisions of
![]() $ {\sigma}_{\boldsymbol{\mu}}={4.3}^{\circ } $
for orientation,
$ {\sigma}_{\boldsymbol{\mu}}={4.3}^{\circ } $
for orientation,
![]() $ {\sigma}_{xy}=11 $
nm for lateral position, and
$ {\sigma}_{xy}=11 $
nm for lateral position, and
![]() $ {\sigma}_z=33.6 $
nm for axial position with a median of 3900 signal photons and 80 background photons/pixel detected (see Image analysis methods for details on Arrowhead DSF analysis and estimation).
$ {\sigma}_z=33.6 $
nm for axial position with a median of 3900 signal photons and 80 background photons/pixel detected (see Image analysis methods for details on Arrowhead DSF analysis and estimation).
Polarization modulation
Besides modulating the phase at the BFP, one can also manipulate fluorescence polarization, i.e., apply spatially varying polarization rotation in the BFP before polarization splitting, to measure SM orientation. In this case, the cross elements
![]() $ {J}_{12}\left(u,v\right) $
and
$ {J}_{12}\left(u,v\right) $
and
![]() $ {J}_{21}\left(u,v\right) $
are no longer zero. For polarization-only modulation, the optical component can be described by a spatially varying real tensor, e.g., separating the radially and azimuthally polarized fluorescence by placing a vortex (half) wave plate (Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022), or equivalently, a y-phi mask (Backlund et al., Reference Backlund, Arbabi, Petrov, Arbabi, Saurabh, Faraon and Moerner2016) or two SLMs (Hashimoto et al., Reference Hashimoto, Yoshiki, Kurihara, Hashimoto and Araki2015), at the BFP. The design rationale is based on the toroidal emission pattern of dipole emitters; a molecule oriented along the optical axis
$ {J}_{21}\left(u,v\right) $
are no longer zero. For polarization-only modulation, the optical component can be described by a spatially varying real tensor, e.g., separating the radially and azimuthally polarized fluorescence by placing a vortex (half) wave plate (Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022), or equivalently, a y-phi mask (Backlund et al., Reference Backlund, Arbabi, Petrov, Arbabi, Saurabh, Faraon and Moerner2016) or two SLMs (Hashimoto et al., Reference Hashimoto, Yoshiki, Kurihara, Hashimoto and Araki2015), at the BFP. The design rationale is based on the toroidal emission pattern of dipole emitters; a molecule oriented along the optical axis
![]() $ z $
emits radially polarized light. Separating the radially polarized light from the azimuthal polarization improves one’s sensitivity to detect changes in polar angle; the relevant real tensor is given by
$ z $
emits radially polarized light. Separating the radially polarized light from the azimuthal polarization improves one’s sensitivity to detect changes in polar angle; the relevant real tensor is given by
This method, termed the radially and azimuthally polarized (raPol) standard DSF (Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022), exhibits excellent orientation measurement performance; with 5000 signal photons and 30 background photons/pixel detected, it achieves precisions of
![]() $ {\sigma}_{\theta }={1.7}^{\circ } $
,
$ {\sigma}_{\theta }={1.7}^{\circ } $
,
![]() $ {\sigma}_{\phi }={1.4}^{\circ } $
, and
$ {\sigma}_{\phi }={1.4}^{\circ } $
, and
![]() $ {\sigma}_{\Omega}=0.16 $
sr. Further, due to its more compact size compared to other engineered DSFs (Figure 7f), it exhibits a localization precision of
$ {\sigma}_{\Omega}=0.16 $
sr. Further, due to its more compact size compared to other engineered DSFs (Figure 7f), it exhibits a localization precision of
![]() $ {\sigma}_{xy}=2.2 $
nm under the aforementioned SBR, comparable to that using the
$ {\sigma}_{xy}=2.2 $
nm under the aforementioned SBR, comparable to that using the
![]() $ x $
and
$ x $
and
![]() $ y $
polarized standard DSF. Its detectability under low SBR is also comparable to
$ y $
polarized standard DSF. Its detectability under low SBR is also comparable to
![]() $ xy $
Pol and is superior to those of other engineered DSFs. It has been shown that measuring molecule locations in the azimuthally polarized channel removes orientation-induced localization bias (Backlund et al., Reference Backlund, Arbabi, Petrov, Arbabi, Saurabh, Faraon and Moerner2016). Given its superior sensitivity to detecting
$ xy $
Pol and is superior to those of other engineered DSFs. It has been shown that measuring molecule locations in the azimuthally polarized channel removes orientation-induced localization bias (Backlund et al., Reference Backlund, Arbabi, Petrov, Arbabi, Saurabh, Faraon and Moerner2016). Given its superior sensitivity to detecting
![]() $ z $
-oriented molecules [Figure 7f(3)] and excellent localization and orientation precision (Zhang and Lew, Reference Zhang and Lew2021b), it was used to image NR molecules within planar SLBs and resolved coupling between absorption and emission dipole orientations. It also detected changes in translational and rotational diffusions of NR molecules induced by cholesterol (Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022).
$ z $
-oriented molecules [Figure 7f(3)] and excellent localization and orientation precision (Zhang and Lew, Reference Zhang and Lew2021b), it was used to image NR molecules within planar SLBs and resolved coupling between absorption and emission dipole orientations. It also detected changes in translational and rotational diffusions of NR molecules induced by cholesterol (Zhang et al., Reference Zhang, Zhou, Lu, Wu and Lew2022).
The recently introduced Multi-View Reflector (MVR) microscope (Figure 7j) further extends SMOLM’s capabilities (Zhang et al., Reference Zhang, Guo, He, Wu, Vahey and Lew2023). In addition to separating radially and azimuthally polarized fluorescence, it incorporates two sets of pyramid mirrors to split light at the BFP and creates eight detection channels. The system’s DSF exhibits similar characteristics to multi-spot DSFs; the relative intensity and position of spots within each channel indicate the orientation and axial position of the emitter, respectively. Despite the complexity of this system (Figure 8c), it showcases remarkable robustness to background fluorescence; since background photons are spread across the eight detection channels along with the signal photons, its effective SBR is better than those of multi-spot DSFs. While imaging SLBs on silica spheres, the MVR microscope experimentally achieves an isotropic 3D localization precision of 10.9 nm and orientation precision of
![]() $ {2.0}^{\circ } $
across a 1.5-micron axial range. It also showed great robustness against aberrations induced by refractive-index mismatches and was used for studying Aβ42-membrane interactions and heterogeneities in fixed HEK-293T cell membranes.
$ {2.0}^{\circ } $
across a 1.5-micron axial range. It also showed great robustness against aberrations induced by refractive-index mismatches and was used for studying Aβ42-membrane interactions and heterogeneities in fixed HEK-293T cell membranes.
Unlike phase-only and polarization-only modulations of the fluorescence at the BFP, Coordinate and Height super-resolution Imaging with Dithering and Orientation (CHIDO) (Ramkhalawon et al., Reference Ramkhalawon, Brown and Alonso2013; Vella and Alonso, Reference Vella and Alonso2019; Curcio et al., Reference Curcio, Alemán-Castañeda, Brown, Brasselet and Alonso2020) uses a single stressed-engineered optic (SEO) to modulate both phase and polarization simultaneously. Its complex tensor is given by
It creates a set of linearly independent basis images that rotate when a molecule is defocused (Figure 7h). The precise features and the performance of this DSF depend on the stress coefficient
![]() $ {c}_{\mathrm{st}} $
(
$ {c}_{\mathrm{st}} $
(
![]() $ 1.2\pi $
in Figure 7h). With 40,000 signal photons detected, CHIDO experimentally achieves a lateral localization precision of
$ 1.2\pi $
in Figure 7h). With 40,000 signal photons detected, CHIDO experimentally achieves a lateral localization precision of
![]() $ {\sigma}_{xy}=13 $
nm, an axial localization precision of
$ {\sigma}_{xy}=13 $
nm, an axial localization precision of
![]() $ {\sigma}_z=50 $
nm, and a precision for measuring the wobble angle
$ {\sigma}_z=50 $
nm, and a precision for measuring the wobble angle
![]() $ {\sigma}_{\Omega}=0.9 $
for molecules attached to F-actin filaments whose tilt angles from the fiber are within
$ {\sigma}_{\Omega}=0.9 $
for molecules attached to F-actin filaments whose tilt angles from the fiber are within
![]() $ {20}^{\circ } $
.
$ {20}^{\circ } $
.
Choosing the appropriate technique for SMOLM
With a myriad of techniques developed in recent years, choosing an SMOLM design can be daunting. Recent studies adapt classical and quantum estimation theory to find optimal imaging systems for both SMLM (Tsang, Reference Tsang2015; Tsang et al., Reference Tsang, Nair and Lu2016; Lupo and Pirandola, Reference Lupo and Pirandola2016; Rehacek et al., Reference Rehacek, Paúr, Stoklasa, Hradil and Sánchez-Soto2017; Ang et al., Reference Ang, Nair and Tsang2017; Backlund et al., Reference Backlund, Shechtman and Walsworth2018; Tsang, Reference Tsang2019; Prasad and Yu, Reference Prasad and Yu2019) and SMOLM (Zhang and Lew, Reference Zhang and Lew2019, Reference Zhang and Lew2020, Reference Zhang and Lew2021a; Beckwith and Yang, Reference Beckwith and Yang2021). For example, in the absence of background photons, one must minimize the phase variation in the detected optical field in order to measure the molecular orientation of rotationally fixed molecules as precisely as possible (Zhang and Lew, Reference Zhang and Lew2020). With these performance limits, one can compare existing methods and evaluate how efficient a technique is at extracting maximum information from a fixed number of signal photons.
Here, we recommend choosing specific criteria based upon the target sample and measurement task. Various advantages and limitations of each approach are summarized in Table 2. In absorption-based techniques, the choice of excitation and detection strategies depends on the expected orientation and rotational dynamics of the target molecules. When most molecules align perpendicularly to the optical axis, using a standard epifluorescence excitation beam traveling along the optical axis of the objective lens with multiple in-plane polarizations is adequate for studying orientational characteristics; see, for example, (Backer et al., Reference Backer, Lee and Moerner2016). In contrast, when the molecular orientation exhibits a prominent axial component, it becomes necessary to either integrate emission polarization separation or implement 3D polarization modulation through tilted illumination (Thorsen et al., Reference Thorsen, Hulleman, Rieger and Stallinga2022).
Table 2. Applications, benefits, and limitations of techniques for SMOLM

For emission-based methods, we follow a recent work (Zhang and Lew, Reference Zhang and Lew2021b) to compare some of the aforementioned DSFs using Fisher information. From estimation theory, the best-possible standard deviation of any unbiased estimator is given by the square root of the Cramér-Rao lower bound (CRB), which is the inverse of the Fisher information matrix (Chao et al., Reference Chao, Sally Ward and Ober2016). Critically, DSFs whose spatial intensity distribution
![]() $ \boldsymbol{I} $
changes more strongly with orientation exhibit superior sensitivity for measuring SM orientation. DSFs with more compact footprints, e.g.,
$ \boldsymbol{I} $
changes more strongly with orientation exhibit superior sensitivity for measuring SM orientation. DSFs with more compact footprints, e.g.,
![]() $ xy $
Pol, raPol, vortex DSFs, pixOL, and CHIDO, generally exhibit superior measurement precision compared to DSFs that are spread over a larger area, e.g., the DH DSF and multi-spot DSFs. Intuitively, they also are easier to detect above noise and therefore are more suitable in SM experiments whose photon budgets are limited. As shown in Figure 9a-d, raPol exhibits the highest overall position-orientation precision in thin samples for SMs at the coverslip-sample interface when the sample is defocused by approximately 200 nm. Other compact DSFs also perform well, similarly outperforming larger DSFs including the MVR microscope. However, a key disadvantage is that the subtle features of the DSFs must be measured with high sensitivity to obtain precise and accurate estimates of SM orientations and positions. Therefore, performance may degrade due to optical aberrations or miscalibration of the system. For example, CHIDO performs 5–6 times worse in experiments compared to the CRB (Curcio et al., Reference Curcio, Alemán-Castañeda, Brown, Brasselet and Alonso2020; Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021). Moreover, performance degradation may be worse when imaging deeply within biological tissues. In contrast, larger DSFs that encode SM orientations in the relative brightness of their spots and SM (axial) position in the positions of the spots are more robust to optical aberrations; precise shape-fitting is not as critical. For example, the MVR microscope exhibits both excellent measurement precision and robustness against aberrations. Further, it exhibits better precision compared to compact DSFs in thick samples over a depth range of 1.5 microns (Figure 9e–h). However, it requires careful alignment of a complex optical system.
$ xy $
Pol, raPol, vortex DSFs, pixOL, and CHIDO, generally exhibit superior measurement precision compared to DSFs that are spread over a larger area, e.g., the DH DSF and multi-spot DSFs. Intuitively, they also are easier to detect above noise and therefore are more suitable in SM experiments whose photon budgets are limited. As shown in Figure 9a-d, raPol exhibits the highest overall position-orientation precision in thin samples for SMs at the coverslip-sample interface when the sample is defocused by approximately 200 nm. Other compact DSFs also perform well, similarly outperforming larger DSFs including the MVR microscope. However, a key disadvantage is that the subtle features of the DSFs must be measured with high sensitivity to obtain precise and accurate estimates of SM orientations and positions. Therefore, performance may degrade due to optical aberrations or miscalibration of the system. For example, CHIDO performs 5–6 times worse in experiments compared to the CRB (Curcio et al., Reference Curcio, Alemán-Castañeda, Brown, Brasselet and Alonso2020; Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021). Moreover, performance degradation may be worse when imaging deeply within biological tissues. In contrast, larger DSFs that encode SM orientations in the relative brightness of their spots and SM (axial) position in the positions of the spots are more robust to optical aberrations; precise shape-fitting is not as critical. For example, the MVR microscope exhibits both excellent measurement precision and robustness against aberrations. Further, it exhibits better precision compared to compact DSFs in thick samples over a depth range of 1.5 microns (Figure 9e–h). However, it requires careful alignment of a complex optical system.

Figure 9. Best-possible precisions, given by the square root of the Cramér-Rao lower bound, of measuring SM position and orientation in (a–d) thin and (e–h) thick samples using various SMOLM techniques. For thin samples, we report precisions of (a) the average orientation
![]() $ \boldsymbol{\mu} $
, (b) wobble angle
$ \boldsymbol{\mu} $
, (b) wobble angle
![]() $ \Omega $
, (c) 2D position
$ \Omega $
, (c) 2D position
![]() $ x $
, and (d) combined precision for orientational second moments
$ x $
, and (d) combined precision for orientational second moments
![]() $ \boldsymbol{m} $
and 2D position
$ \boldsymbol{m} $
and 2D position
![]() $ x $
as a function of nominal focal plane position
$ x $
as a function of nominal focal plane position
![]() $ {z}_f $
. All SMs are positioned at
$ {z}_f $
. All SMs are positioned at
![]() $ z=0 $
nm (at the glass-media interface). For thick samples, we report precisions of (e) average orientation
$ z=0 $
nm (at the glass-media interface). For thick samples, we report precisions of (e) average orientation
![]() $ \boldsymbol{\mu} $
, (f) wobble angle
$ \boldsymbol{\mu} $
, (f) wobble angle
![]() $ \Omega $
, (g) 3D position
$ \Omega $
, (g) 3D position
![]() $ \boldsymbol{r} $
, and (h) combined precision for orientational second moments
$ \boldsymbol{r} $
, and (h) combined precision for orientational second moments
![]() $ \boldsymbol{m} $
and 3D position
$ \boldsymbol{m} $
and 3D position
![]() $ \boldsymbol{r} $
as a function of molecular position
$ \boldsymbol{r} $
as a function of molecular position
![]() $ z $
. The nominal focal plane is set at
$ z $
. The nominal focal plane is set at
![]() $ {z}_f=1200 $
nm. For all simulations, we assume that the sample has a refractive index
$ {z}_f=1200 $
nm. For all simulations, we assume that the sample has a refractive index
![]() $ {n}_2=1.33 $
(equal to that of water) and that 5000 signal photons and 40 background photons per pixel total across all channels are collected. See (Zhang and Lew, Reference Zhang and Lew2021b) for details on how each quantity is defined and calculated.
$ {n}_2=1.33 $
(equal to that of water) and that 5000 signal photons and 40 background photons per pixel total across all channels are collected. See (Zhang and Lew, Reference Zhang and Lew2021b) for details on how each quantity is defined and calculated.
Image analysis methods
Accurately and precisely estimating the position and orientation of molecules is crucial for SMOLM; a selection of publicly available software is summarized in Table 3. Many SMOLM algorithms separate the detection and estimation tasks; they first detect and localize SMs and then subsequently estimate their orientations (Figure 10a). For example, to detect smaller DSFs such as pixOL (Wu et al., Reference Wu, Lu and Lew2022a), one might use the images of an in-focus emitter or Gaussian DSF for detection and localization. Orientation estimation and (3D) position refinement can be achieved using pattern matching (Patra et al., Reference Patra, Gregor and Enderlein2004; Aguet et al., Reference Aguet, Geissbühler, Märki, Lasser and Unser2009) or maximum likelihood estimation (MLE) (Hulleman et al., Reference Hulleman, Thorsen, Kim, Dekker, Stallinga and Rieger2021). In contrast, 2D and/or 3D localization of the double-helix DSF and multi-spot DSFs involve localizing the spots, either by fitting Gaussian spots (Backlund et al., Reference Backlund, Lew, Backer, Sahl, Grover, Agrawal, Piestun and Moerner2012; Backer et al., Reference Backer, Backlund, von Diezmann, Sahl and Moerner2014) or employing other algorithms like ThunderSTORM (Ovesný et al., Reference Ovesný, Křížek, Borkovec, Švindrych and Hagen2014; Zhang et al., Reference Zhang, Lu, Ding and Lew2018). The orientation can be calculated by using the spot brightness ratio or directly estimated using an MLE.
Table 3. Publicly available image analysis software for SMOLM

Figure 10. Workflow of detection and estimation algorithms in SMOLM. (a) A raw fluorescence image can be processed using (i) an SM detection algorithm. (ii) The detected SM images can be fitted to the forward imaging model using an MLE; a reconstruction of the raw image using the fit parameters is shown in (iii). (b) The image can also be fitted to the forward imaging model using a sparsity-promoting MLE (reconstruction shown in (b)), or (c) through a (i) convolutional neural network that generates an (ii) upsampled stack representing the position and orientation of SMs. The final output of these algorithms is a list of SM positions and orientations.
Here, we show MLE for estimating the second-order orientational moments
![]() $ \boldsymbol{m} $
. Other orientational parameters, such as the Stokes parameters, can be estimated similarly as long as a forward model is written that explicitly models both signal and noise within the detected images. We assume that the number of detected photons at pixel
$ \boldsymbol{m} $
. Other orientational parameters, such as the Stokes parameters, can be estimated similarly as long as a forward model is written that explicitly models both signal and noise within the detected images. We assume that the number of detected photons at pixel
![]() $ i $
follows a Poisson distribution, i.e.,
$ i $
follows a Poisson distribution, i.e.,
![]() $ {\hat{I}}_i\sim \mathrm{Poisson}\left({I}_i+{b}_i\right) $
, where
$ {\hat{I}}_i\sim \mathrm{Poisson}\left({I}_i+{b}_i\right) $
, where
![]() $ {I}_i $
is given by Eq. (45) and
$ {I}_i $
is given by Eq. (45) and
![]() $ {b}_i $
represents the expected background. Therefore, the estimated brightness and the second-order moment vector are estimated by minimizing the Poisson negative log-likelihood (NLL), i.e.,
$ {b}_i $
represents the expected background. Therefore, the estimated brightness and the second-order moment vector are estimated by minimizing the Poisson negative log-likelihood (NLL), i.e.,
This equation can be further refined using a first-order approximation by including the gradient of
![]() $ \boldsymbol{B} $
with respect to the molecule’s 3D position for robust, computationally efficient subpixel-scale localization (Mazidi et al., Reference Mazidi, King, Zhang, Nehorai and Lew2019). The second moments
$ \boldsymbol{B} $
with respect to the molecule’s 3D position for robust, computationally efficient subpixel-scale localization (Mazidi et al., Reference Mazidi, King, Zhang, Nehorai and Lew2019). The second moments
![]() $ \hat{\boldsymbol{m}} $
can be mapped to the first-order transition dipole moments
$ \hat{\boldsymbol{m}} $
can be mapped to the first-order transition dipole moments
![]() $ \hat{\boldsymbol{\mu}} $
and wobble
$ \hat{\boldsymbol{\mu}} $
and wobble
![]() $ \hat{\Omega} $
using a Fisher information (FI)-weighted, mean square-error cost function, i.e.,
$ \hat{\Omega} $
using a Fisher information (FI)-weighted, mean square-error cost function, i.e.,
where
![]() $ {\boldsymbol{m}}^{\prime } $
is given by Eq. (37).
$ {\boldsymbol{m}}^{\prime } $
is given by Eq. (37).
A significant drawback of separating the detection and estimation algorithms is the difficulty in handling high molecular density, thus restricting acquisition speed. An alternative strategy is to leverage the inherent sparsity of SM blinking in SMOLM experiments through a regularized MLE (Figure 10b) and solve the molecular detection and position and orientation estimation tasks simultaneously. Instead of minimizing the Poisson NLL, a sparsity-promoting regularizer, e.g., the
![]() $ \ell $
2 norm of intensity-weighted second moments
$ \ell $
2 norm of intensity-weighted second moments
![]() $ \hat{\boldsymbol{m}} $
associated with each spatial grid point, is added to the cost function. Mazidi et al. demonstrated that such an algorithm performs closely to the theoretical bound given by the CRB even in highly overlapping areas (Mazidi et al., Reference Mazidi, King, Zhang, Nehorai and Lew2019). However, one limitation, especially for 3D SMOLM, is that iterative optimization algorithms tend to be computationally expensive and slow (Bruggeman et al., Reference Bruggeman, Zhang, Needham, Körbel, Daly, Cheetham, Peters, Wu, Klymchenko, Davis, Paluch, Klenerman, Lew, O’Holleran and Lee2024).
$ \hat{\boldsymbol{m}} $
associated with each spatial grid point, is added to the cost function. Mazidi et al. demonstrated that such an algorithm performs closely to the theoretical bound given by the CRB even in highly overlapping areas (Mazidi et al., Reference Mazidi, King, Zhang, Nehorai and Lew2019). However, one limitation, especially for 3D SMOLM, is that iterative optimization algorithms tend to be computationally expensive and slow (Bruggeman et al., Reference Bruggeman, Zhang, Needham, Körbel, Daly, Cheetham, Peters, Wu, Klymchenko, Davis, Paluch, Klenerman, Lew, O’Holleran and Lee2024).
Recently, deep learning, particularly convolutional neural networks (CNNs), has emerged as a powerful tool for SM image analysis due to its superior pattern recognition capabilities. Inspired by recent advancements in CNN-based 3D localization algorithms (Möckl et al., Reference Möckl, Roy and Moerner2020; Nehme et al., Reference Nehme, Freedman, Gordon, Ferdman, Weiss, Alalouf, Naor, Orange, Michaeli and Shechtman2020; Speiser et al., Reference Speiser, Müller, Hoess, Matti, Obara, Legant, Kreshuk, Macke, Ries and Turaga2021), Wu et al. introduced an approach named Deep-SMOLM to detect SMs and simultaneously estimate their 2D positions and 3D orientations (Wu et al., Reference Wu, Lu, Rahman, Li and Lew2022b) (Figure 10c). Two polarized images are input to the NN, and six upsampled images are produced, each representing the 2D spatial distribution of one of the six second-order orientational moments. A post-processing step converts these images into a list of 2D positions and 3D orientations. Using both simulated and experimentally acquired images with highly overlapping pixOL DSFs, the NN demonstrates measurement precision close to the theoretical limit (3.8° orientation, 0.32 sr wobble angle, and 8.5 nm lateral position using 1000 detected photons) and a tenfold improvement in speed over iterative approaches. The aforementioned Arrowhead DSF also makes use of an NN for position and orientation estimation (Jouchet et al., Reference Jouchet, Roy and Moerner2023). First, SMs within the field of view are coarsely located using the standard DSF (e.g., by turning off the SLM), and then centered and cropped ROIs containing the Arrowhead DSF are fed to the analysis NN to produce 3D position and 3D orientation estimates. The NN was able to analyze ~150,000 DSF images at a rate of 4 ms per molecule. Clearly, the use of NNs for SMOLM image analysis holds tremendous promise for accelerating precise 6D measurements of SMs.
Conclusion and outlook
In this review, we have explored the latest advancements in SMOLM, highlighting its expanding role across various research areas. Our discussion spans a range of innovative labeling techniques and advanced imaging methods that offer unparalleled insights into molecular orientations and dynamics. Recent work highlights the crucial roles of fluorescent probes for visualizing the complex organization and dynamics of actin filaments, DNA structures, amyloid aggregates, and cellular membranes, among others. Additionally, we have reviewed various imaging techniques that underscore both the potential and the challenges of SMOLM. These methods aim to optimize the measurement of molecular orientations from multiple perspectives, including the fundamental physics of light-matter interactions as well as principles of estimation theory. Further, the incorporation of advanced computational tools improves the accuracy and precision of these measurements. Overall, the insights presented in this review underscore how SMOLM advances our understanding of biological and biochemical processes at the nanoscale.
As we envision the future of SMOLM, several developments are key to further expanding its capabilities and adoption in biophysical studies. The development of new fluorescent probes is crucial for advancing SMOLM (Grimm et al., Reference Grimm, Tkachuk, Patel, Hennigan, Gutu, Dong, Gandin, Osowski, Holland, Liu, Brown and Lavis2023). Future probes should aim for enhanced photostability, higher quantum yield, and improved binding specificity to target structures, while also minimizing perturbative effects. These improvements would significantly enhance the SBR in SMOLM measurements by boosting signal levels and reducing the off-structure background. Improved brightness (photons/s) is particularly critical when studying the orientational dynamics of SMs in the complex environments of biological systems. Engineering new probes that specifically bind to certain biomarkers or protein domains, react to cellular environmental changes, and change their optical properties in response to specific chemical interactions and environments will also be particularly beneficial (Kikuchi et al., Reference Kikuchi, Adair, Lin, New and Kaur2023; Wu et al., Reference Wu, King, Qiu, Farag, Pappu and Lew2023; Bhuskute et al., Reference Bhuskute, Kikuchi, Luo and Kaur2024; Erkamp et al., Reference Erkamp, Farag, Qiu, Quan, Sneideris, Wu, Welsh, Ausserwӧger, Krug, Weitz, Lew, Knowles and Pappu2024; Zhu et al., Reference Zhu, Mei, Tian, Li, Wang, Xiang, M-Q and Tang2024).
Continuous innovation in imaging systems is essential for overcoming the limitations of existing methods and achieving accurate, precise, and robust measurements. Measurement precision could be further enhanced by using adaptive hardware, where the imaging system is iteratively updated to progressively measure the orientation of a single molecule more precisely, as is done for molecular positions in MINFLUX (Balzarotti et al., Reference Balzarotti, Eilers, Gwosch, Gynnå, Westphal, Stefani, Elf and Hell2017; Cnossen et al., Reference Cnossen, Hinsdale, Thorsen, Siemons, Schueder, Jungmann, Smith, Rieger and Stallinga2020; Gwosch et al., Reference Gwosch, Pape, Balzarotti, Hoess, Ellenberg, Ries and Hell2020; Weber et al., Reference Weber, Von Der Emde, Leutenegger, Gunkel, Sambandan, Khan, Keller-Findeisen, Cordes and Hell2023; Sahl et al., Reference Sahl, Matthias, Inamdar, Weber, Khan, Brüser, Jakobs, Becker, Griesinger, Broichhagen and Hell2024). Recent developments in single-photon avalanche diode (SPAD) array detectors (Bucci et al., Reference Bucci, Tortarolo, Held, Bega, Perego, Castagnetti, Bozzoni, Slenders and Vicidomini2024) have the potential to provide precise photon arrival timing as well as location information for SMOLM, thereby enabling SMOLM to probe faster biochemical processes including protein folding and conformational dynamics. Existing emission-based methods (engineered DSFs) could be combined with selective illumination techniques like light-sheet illumination (Gustavsson et al., Reference Gustavsson, Petrov, Lee, Shechtman and Moerner2018; Nelson et al., Reference Nelson, Vargas-Hernández, Freire, Cheng and Gustavsson2024) to improve the SBR. Further, measuring higher-order orientational moments, i.e., measuring absorption and emission dipole moments simultaneously using both excitation and emission modulation, could enable more detailed studies of rotational dynamics with improved angular resolution (Chen et al., Reference Chen, Qiu and Lew2024b). In these ways, each precious fluorescence photon can be utilized more efficiently for higher precision measurements.
Advanced computational imaging techniques will also play a significant role in the future of SMOLM. The integration of modern computer vision methodologies, such as neural fields (Park et al., Reference Park, Florence, Straub, Newcombe and Lovegrove2019; Mildenhall et al., Reference Mildenhall, Srinivasan, Tancik, Barron, Ramamoorthi and Ng2022; Zhou et al., Reference Zhou, Feng, Guo, Lin, Liang, Metzler and Yang2023; Zhang et al., Reference Zhang, Zhou, Feng, Larsson, Alcalde, Yin, Deng and Yang2024) or diffusion models (Waibel et al., Reference Waibel, Röell, Rieck, Giryes and Marr2023; Hui et al., Reference Hui, Wei, Zhu, Xia and Zhou2024), could potentially improve estimation performance, allowing for the extraction of more detailed information from larger and more complex datasets. Especially when engineered DSFs and estimation algorithms are optimized jointly, these computational advances could potentially handle images with higher molecular density, thereby improving imaging speed and overall data throughput.
With numerous opportunities for technological innovation, we expect SMOLM to have significant contributions to elucidating the nanoscale organization and dynamics of biological and chemical systems in the near future. Higher precision measurements of both 3D position and 3D orientation have a unique power to reveal new insights, and we eagerly anticipate SMOLM to have far-ranging applications from understanding fundamental biological processes to developing new materials and nanotechnologies.
Acknowledgements
We thank Tianben Ding and Tingting Wu for helpful discussions when preparing this manuscript.
Financial support
Research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R35GM124858 to M.D.L.
Competing interest
The authors declare none.