Article contents
Minimum φ-Divergence Estimation in Constrained Latent Class Models for Binary Data
Published online by Cambridge University Press: 01 January 2025
Abstract
The main purpose of this paper is to introduce and study the behavior of minimum ϕ\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\phi $$\end{document}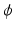 -divergence estimators as an alternative to the maximum-likelihood estimator in latent class models for binary items. As it will become clear below, minimum ϕ\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\phi $$\end{document}
-divergence estimators as an alternative to the maximum-likelihood estimator in latent class models for binary items. As it will become clear below, minimum ϕ\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\phi $$\end{document}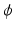 -divergence estimators are a natural extension of the maximum-likelihood estimator. The asymptotic properties of minimum ϕ\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\phi $$\end{document}
-divergence estimators are a natural extension of the maximum-likelihood estimator. The asymptotic properties of minimum ϕ\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\phi $$\end{document}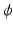 -divergence estimators for latent class models for binary data are developed. Finally, to compare the efficiency and robustness of these new estimators with that obtained through maximum likelihood when the sample size is not big enough to apply the asymptotic results, we have carried out a simulation study.
-divergence estimators for latent class models for binary data are developed. Finally, to compare the efficiency and robustness of these new estimators with that obtained through maximum likelihood when the sample size is not big enough to apply the asymptotic results, we have carried out a simulation study.
Keywords
Information
- Type
- Original Paper
- Information
- Copyright
- Copyright © 2015 The Psychometric Society
References
- 4
- Cited by

