Article contents
The Geometry of Enhancement in Multiple Regression
Published online by Cambridge University Press: 01 January 2025
Abstract
In linear multiple regression, “enhancement” is said to occur when R2=b′r>r′r, where b is a p×1 vector of standardized regression coefficients and r is a p×1 vector of correlations between a criterion y and a set of standardized regressors, x. When p=1 then b≡r and enhancement cannot occur. When p=2, for all full-rank Rxx≠I, Rxx=E[xx′]=VΛV′ (where VΛV′ denotes the eigen decomposition of Rxx; λ1>λ2), the set \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\boldsymbol{B}_{1}:=\{\boldsymbol{b}_{i}:R^{2}=\boldsymbol{b}_{i}'\boldsymbol{r}_{i}=\boldsymbol{r}_{i}'\boldsymbol{r}_{i};0 \ltR^{2}\le1\}$\end{document}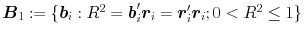 contains four vectors; the set \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\boldsymbol{B}_{2}:=\{\boldsymbol{b}_{i}: R^{2}=\boldsymbol{b}_{i}'\boldsymbol{r}_{i}\gt\boldsymbol{r}_{i}'\boldsymbol{r}_{i}$\end{document}
contains four vectors; the set \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\boldsymbol{B}_{2}:=\{\boldsymbol{b}_{i}: R^{2}=\boldsymbol{b}_{i}'\boldsymbol{r}_{i}\gt\boldsymbol{r}_{i}'\boldsymbol{r}_{i}$\end{document}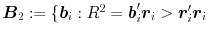 ; \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$0\lt R^{2}\le1;R^{2}\lambda_{p}\leq\boldsymbol{r}_{i}'\boldsymbol{r}_{i}\lt R^{2}\}$\end{document}
; \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$0\lt R^{2}\le1;R^{2}\lambda_{p}\leq\boldsymbol{r}_{i}'\boldsymbol{r}_{i}\lt R^{2}\}$\end{document}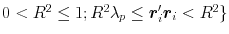 contains an infinite number of vectors. When p≥3 (and λ1>λ2>⋯>λp), both sets contain an uncountably infinite number of vectors. Geometrical arguments demonstrate that B1 occurs at the intersection of two hyper-ellipsoids in ℝp. Equations are provided for populating the sets B1 and B2 and for demonstrating that maximum enhancement occurs when b is collinear with the eigenvector that is associated with λp (the smallest eigenvalue of the predictor correlation matrix). These equations are used to illustrate the logic and the underlying geometry of enhancement in population, multiple-regression models. R code for simulating population regression models that exhibit enhancement of any degree and any number of predictors is included in Appendices A and B.
contains an infinite number of vectors. When p≥3 (and λ1>λ2>⋯>λp), both sets contain an uncountably infinite number of vectors. Geometrical arguments demonstrate that B1 occurs at the intersection of two hyper-ellipsoids in ℝp. Equations are provided for populating the sets B1 and B2 and for demonstrating that maximum enhancement occurs when b is collinear with the eigenvector that is associated with λp (the smallest eigenvalue of the predictor correlation matrix). These equations are used to illustrate the logic and the underlying geometry of enhancement in population, multiple-regression models. R code for simulating population regression models that exhibit enhancement of any degree and any number of predictors is included in Appendices A and B.
Information
- Type
- Original Paper
- Information
- Copyright
- Copyright © 2011 The Psychometric Society
References
- 3
- Cited by

