Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ten Berge, Jos M. F.
1983.
On Green's Best Linear Composites with a Specified Structure, and Oblique Estimates of Factor Scores.
Psychometrika,
Vol. 48,
Issue. 3,
p.
371.
Ramsay, J. O.
ten Berge, Jos
and
Styan, G. P. H.
1984.
Matrix Correlation.
Psychometrika,
Vol. 49,
Issue. 3,
p.
403.
ten Berge, Jos M. F.
de Leeuw, Jan
and
Kroonenberg, Pieter M.
1987.
Some Additional Results on Principal Components Analysis of Three-Mode Data by Means of Alternating Least Squares Algorithms.
Psychometrika,
Vol. 52,
Issue. 2,
p.
183.
Kiers, Henk A.L.
and
Ten Berge, Jos M.F.
1989.
Optimality conditions for the trace of certain matrix products.
Linear Algebra and its Applications,
Vol. 126,
Issue. ,
p.
125.
Kiers, Henk A. L.
ten Berge, Jos M. F.
Takane, Yoshio
and
de Leeuw, Jan
1990.
A Generalization of Takane's Algorithm for Dedicom.
Psychometrika,
Vol. 55,
Issue. 1,
p.
151.
Kiers, Henk A. L.
1991.
Simple Structure in Component Analysis Techniques for Mixtures of Qualitative and Quantitative Variables.
Psychometrika,
Vol. 56,
Issue. 2,
p.
197.
ten Berge, Jos M. F.
Bekker, Paul A.
and
Kiers, Henk A. L.
1994.
Some Clarifications of the TUCKALS2 Algorithm Applied to the IDIOSCAL Problem.
Psychometrika,
Vol. 59,
Issue. 2,
p.
193.
Kiers, Henk A. L.
1995.
Maximization of Sums of Quotients of Quadratic Forms and Some Generalizations.
Psychometrika,
Vol. 60,
Issue. 2,
p.
221.
ten Berge, Jos M.F.
Krijnen, Wim P.
Wansbeek, Tom
and
Shapiro, Alexander
1999.
Some new results on correlation-preserving factor scores prediction methods.
Linear Algebra and its Applications,
Vol. 289,
Issue. 1-3,
p.
311.
Takane, Yoshio
2004.
Matrices with special reference to applications in psychometrics.
Linear Algebra and its Applications,
Vol. 388,
Issue. ,
p.
341.
Ten Berge, Jos M. F.
2005.
J.C. Gower and G.B. Dijksterhuis. Procrustes problems. New York: Oxford University Press, 2004, xiv + 233 pp., $102.69..
Psychometrika,
Vol. 70,
Issue. 4,
p.
799.
YAMASHITA, Naoto
2012.
Canonical Correlation Analysis Formulated as Maximizing Sum of Squared Correlations and Rotation of Structure Matrices.
Kodo Keiryogaku (The Japanese Journal of Behaviormetrics),
Vol. 39,
Issue. 1,
p.
1.
Adachi, Kohei
2012.
<b>SOME CONTRIBUTIONS TO DATA-FITTING FACTOR </b><b>ANALYSIS WITH EMPIRICAL COMPARISONS TO </b><b>COVARIANCE-FITTING FACTOR ANALYSIS </b>.
Journal of the Japanese Society of Computational Statistics,
Vol. 25,
Issue. 1,
p.
25.
Adachi, Kohei
2013.
<b>A RESTRAINED CONDITION NUMBER LEAST SQUARES TECHNIQUE WITH ITS APPLICATIONS TO AVOIDING </b><b>RANK DEFICIENCY </b>.
Journal of the Japanese Society of Computational Statistics,
Vol. 26,
Issue. 1,
p.
39.
Satomura, Hironori
and
Adachi, Kohei
2013.
Oblique Rotaton in Canonical Correlation Analysis Reformulated as Maximizing the Generalized Coefficient of Determination.
Psychometrika,
Vol. 78,
Issue. 3,
p.
526.
Yamashita, Naoto
and
Mayekawa, Shin-ichi
2015.
A new biplot procedure with joint classification of objects and variables by fuzzy c-means clustering.
Advances in Data Analysis and Classification,
Vol. 9,
Issue. 3,
p.
243.
Uno, Kohei
Satomura, Hironori
and
Adachi, Kohei
2016.
Fixed factor analysis with clustered factor score constraint.
Computational Statistics & Data Analysis,
Vol. 94,
Issue. ,
p.
265.
Ikemoto, Hiroki
and
Adachi, Kohei
2016.
Sparse Tucker2 analysis of three-way data subject to a constrained number of zero elements in a core array.
Computational Statistics & Data Analysis,
Vol. 98,
Issue. ,
p.
1.
Adachi, Kohei
and
Trendafilov, Nickolay T.
2018.
Sparsest factor analysis for clustering variables: a matrix decomposition approach.
Advances in Data Analysis and Classification,
Vol. 12,
Issue. 3,
p.
559.
Adachi, Kohei
and
Trendafilov, Nickolay T.
2018.
Some Mathematical Properties of the Matrix Decomposition Solution in Factor Analysis.
Psychometrika,
Vol. 83,
Issue. 2,
p.
407.
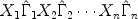 where the matrices \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\hat \Gamma _i$$\end{document}
where the matrices \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\hat \Gamma _i$$\end{document}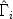 are diagonal and fixed and the Xi vary unrestrictedly and independently over the set of orthonormal matrices. The theorem is a useful tool in deriving maxima and minima of matrix trace functions subject to orthogonality constraints. The present paper contains a generalization of Kristof's theorem to the case where the Xi are merely required to be submatrices of orthonormal matrices and to have a specified maximum rank. The generalized theorem contains the Schwarz inequality as a special case. Various examples from the psychometric literature, illustrating the practical use of the generalized theorem, are discussed.
are diagonal and fixed and the Xi vary unrestrictedly and independently over the set of orthonormal matrices. The theorem is a useful tool in deriving maxima and minima of matrix trace functions subject to orthogonality constraints. The present paper contains a generalization of Kristof's theorem to the case where the Xi are merely required to be submatrices of orthonormal matrices and to have a specified maximum rank. The generalized theorem contains the Schwarz inequality as a special case. Various examples from the psychometric literature, illustrating the practical use of the generalized theorem, are discussed.
