Article contents
Ensuring Positiveness of the Scaled Difference Chi-square Test Statistic
Published online by Cambridge University Press: 01 January 2025
Abstract
A scaled difference test statistic \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\tilde{T}{}_{d}$\end{document}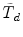 that can be computed from standard software of structural equation models (SEM) by hand calculations was proposed in Satorra and Bentler (Psychometrika 66:507–514, 2001). The statistic \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\tilde{T}_{d}$\end{document}
that can be computed from standard software of structural equation models (SEM) by hand calculations was proposed in Satorra and Bentler (Psychometrika 66:507–514, 2001). The statistic \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\tilde{T}_{d}$\end{document}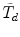 is asymptotically equivalent to the scaled difference test statistic \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\bar{T}_{d}$\end{document}
is asymptotically equivalent to the scaled difference test statistic \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\bar{T}_{d}$\end{document}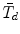 introduced in Satorra (Innovations in Multivariate Statistical Analysis: A Festschrift for Heinz Neudecker, pp. 233–247, 2000), which requires more involved computations beyond standard output of SEM software. The test statistic \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\tilde{T}_{d}$\end{document}
introduced in Satorra (Innovations in Multivariate Statistical Analysis: A Festschrift for Heinz Neudecker, pp. 233–247, 2000), which requires more involved computations beyond standard output of SEM software. The test statistic \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\tilde{T}_{d}$\end{document}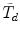 has been widely used in practice, but in some applications it is negative due to negativity of its associated scaling correction. Using the implicit function theorem, this note develops an improved scaling correction leading to a new scaled difference statistic \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\bar{T}_{d}$\end{document}
has been widely used in practice, but in some applications it is negative due to negativity of its associated scaling correction. Using the implicit function theorem, this note develops an improved scaling correction leading to a new scaled difference statistic \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\bar{T}_{d}$\end{document}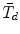 that avoids negative chi-square values.
that avoids negative chi-square values.
Keywords
Information
- Type
- Theory and Methods
- Information
- Copyright
- Copyright © 2010 The Psychometric Society
Footnotes
Research supported by grants SEJ2006-13537 and PR2007-0221 from the Spanish Ministry of Science and Technology and by USPHS grants DA00017 and DA01070.
References
A correction has been issued for this article:
- 1384
- Cited by
Linked content
Please note a has been issued for this article.

