Article contents
Bayesian Inference for an Unknown Number of Attributes in Restricted Latent Class Models
Published online by Cambridge University Press: 01 January 2025
Abstract
The specification of the Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document}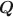 matrix in cognitive diagnosis models is important for correct classification of attribute profiles. Researchers have proposed many methods for estimation and validation of the data-driven Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document}
matrix in cognitive diagnosis models is important for correct classification of attribute profiles. Researchers have proposed many methods for estimation and validation of the data-driven Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document}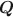 matrices. However, inference of the number of attributes in the general restricted latent class model remains an open question. We propose a Bayesian framework for general restricted latent class models and use the spike-and-slab prior to avoid the computation issues caused by the varying dimensions of model parameters associated with the number of attributes, K. We develop an efficient Metropolis-within-Gibbs algorithm to estimate K and the corresponding Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document}
matrices. However, inference of the number of attributes in the general restricted latent class model remains an open question. We propose a Bayesian framework for general restricted latent class models and use the spike-and-slab prior to avoid the computation issues caused by the varying dimensions of model parameters associated with the number of attributes, K. We develop an efficient Metropolis-within-Gibbs algorithm to estimate K and the corresponding Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document}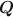 matrix simultaneously. The proposed algorithm uses the stick-breaking construction to mimic an Indian buffet process and employs a novel Metropolis–Hastings transition step to encourage exploring the sample space associated with different values of K. We evaluate the performance of the proposed method through a simulation study under different model specifications and apply the method to a real data set related to a fluid intelligence matrix reasoning test.
matrix simultaneously. The proposed algorithm uses the stick-breaking construction to mimic an Indian buffet process and employs a novel Metropolis–Hastings transition step to encourage exploring the sample space associated with different values of K. We evaluate the performance of the proposed method through a simulation study under different model specifications and apply the method to a real data set related to a fluid intelligence matrix reasoning test.
Keywords
Information
- Type
- Theory and Methods
- Information
- Copyright
- Copyright © 2023 The Author(s) under exclusive licence to The Psychometric Society
References
- 3
- Cited by

