Article contents
Convergence of Estimates of Unique Variances in Factor Analysis, Based on the Inverse Sample Covariance Matrix
Published online by Cambridge University Press: 01 January 2025
Abstract
If the ratio m/p tends to zero, where m is the number of factors m and m the number of observable variables, then the inverse diagonal element of the inverted observable covariance matrix 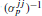 tends to the corresponding unique variance ψjj for almost all of these (Guttman, 1956). If the smallest singular value of the loadings matrix from Common Factor Analysis tends to infinity as p increases, then m/p tends to zero. The same condition is necessary and sufficient for
tends to the corresponding unique variance ψjj for almost all of these (Guttman, 1956). If the smallest singular value of the loadings matrix from Common Factor Analysis tends to infinity as p increases, then m/p tends to zero. The same condition is necessary and sufficient for 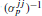 to tend to ψjj for all of these. Several related conditions are discussed.
to tend to ψjj for all of these. Several related conditions are discussed.
Information
- Type
- Original Paper
- Information
- Copyright
- Copyright © 2006 The Psychometric Society
Footnotes
The author is obliged Jos Ten Berge for his comments on the final draft and to the associate editor and the reviewers for their stimulating remarks during the review process.
References
- 10
- Cited by

