Contents
Research Article
Regularity results for equilibria in a variational model for fracture
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 889-902
-
- Article
- Export citation
Stochastic systems governed by B-evolutions on Hilbert spaces
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 903-920
-
- Article
- Export citation
Positive solution curves of semipositone problems with concave nonlinearities*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 921-934
-
- Article
- Export citation
Local existence and blow-up criterion for the Boussinesq equations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 935-946
-
- Article
- Export citation
Positive definite temperature functions and a correspondence to positive temperature functions
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 947-961
-
- Article
- Export citation
Stable summands of U(n)
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 963-973
-
- Article
- Export citation
Singular boundary value problems for P-Laplacian-like equations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 975-981
-
- Article
- Export citation
A perturbation result of semilinear elliptic equations in exterior strip domains
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 983-1004
-
- Article
- Export citation
Regularity of plate equations with control concentrated in interior curves
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1005-1025
-
- Article
- Export citation
The spectrum and eigenspaces of a meromorphic operator-valued function
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1027-1051
-
- Article
- Export citation
Influence of mixed boundary conditions in some reaction–diffusion systems
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1053-1066
-
- Article
- Export citation
The viscous damping prevents propagation of singularities in the system of viscoelasticity
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1067-1074
-
- Article
- Export citation
A combinatorial procedure for finding isolating neighbourhoods and index pairs
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1075-1088
-
- Article
- Export citation
A variational problem on subsets of ℝn
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1089-1101
-
- Article
- Export citation
Convergence of the viscosity solutions for weakly strictly hyperbolic conservation laws*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1103-1110
-
- Article
- Export citation
Erratum
On homotopy conditions and the existence of multiple equilibria in finite elasticity
-
- Published online by Cambridge University Press:
- 14 November 2011, p. 1111
-
- Article
-
- You have access
- Export citation
Front matter
PRM volume 127 issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 127 issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation
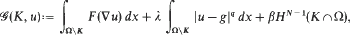
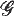 corresponding to polyconvex bulk energy densities of the form
corresponding to polyconvex bulk energy densities of the form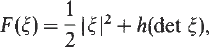
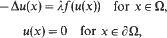
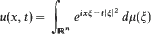
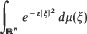
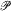 is introduced to give an isomorphism between the class ofall positive definite temperature functions and the class of all possible temperature functions in
is introduced to give an isomorphism between the class ofall positive definite temperature functions and the class of all possible temperature functions in 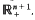 Then correspondence given by
Then correspondence given by