Contents
Research Article
Initial boundary value problems for isentropic gas dynamics
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-23
-
- Article
- Export citation
Homogenisation of a class of fourth order equations with application to incompressible elasticity
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 25-46
-
- Article
- Export citation
The group of homotopy self-equivalences of non-simply-connected spaces using Postnikov decompositions*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 47-60
-
- Article
- Export citation
Smooth conjugacy of centre manifolds
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 61-77
-
- Article
- Export citation
Existence of positive entire solutions for weakly coupled semilinear elliptic systems
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 79-91
-
- Article
- Export citation
The gap phenomenon for variational integrals in Sobolev spaces*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 93-98
-
- Article
- Export citation
Lower semicontinuity of surface energies
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 99-115
-
- Article
- Export citation
Initial conditions for integrable-square solutions to singular differential equations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 117-127
-
- Article
- Export citation
On the semigroups of order-decreasing finite full transformations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 129-142
-
- Article
- Export citation
On periodic solutions for singular perturbation problems
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 143-152
-
- Article
- Export citation
On successive coefficients of univalent functions
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 153-164
-
- Article
- Export citation
Classification of regularly solvable first-order differential operators
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 165-178
-
- Article
- Export citation
On the stability for a population growth equation with time delay
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 179-184
-
- Article
- Export citation
Rank-one convexity does not imply quasiconvexity
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 185-189
-
- Article
- Export citation
Front matter
PRM volume 120 issue 1-2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 120 issue 1-2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation
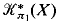 of the representation
of the representation 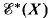 → aut (π
→ aut (π in terms of
in terms of 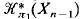 , where
, where 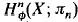 ; and we calculate
; and we calculate  and
and  of self-homotopy-equivalence classes of
of self-homotopy-equivalence classes of 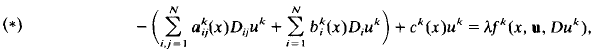
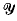 if
if 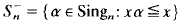 be the subsemigroup of all decreasing maps of Sing
be the subsemigroup of all decreasing maps of Sing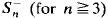 is a non-regular abundant semigroup with
is a non-regular abundant semigroup with 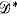 -classes and
-classes and 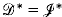 . Moreover,
. Moreover, 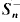 is idempotent-generated and it is generated by the
is idempotent-generated and it is generated by the 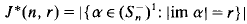
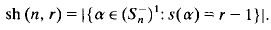
 .
.