Contents
Research Article
Improved estimates and a limit case for the electrostatic Klein–Gordon–Maxwell system
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 449-463
-
- Article
- Export citation
Global strict solutions to continuous coagulation–fragmentation equations with strong fragmentation
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 465-480
-
- Article
- Export citation
Remarks on the existence, uniqueness and semi-explicit solvability of systems of autonomous partial differential equations in divergence form with constant boundary conditions
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 481-495
-
- Article
- Export citation
Diffusive wavelets on groups and homogeneous spaces
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 497-520
-
- Article
- Export citation
Generalized invariant sub- and super-solutions for the energy-decreasing flow
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 521-536
-
- Article
- Export citation
Further study of a fourth-order elliptic equation with negative exponent
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 537-549
-
- Article
- Export citation
A mathematical analysis of tsunami generation in shallow water due to seabed deformation
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 551-608
-
- Article
- Export citation
The Golod-Shafarevich inequality for Hilbert series of quadratic algebras and the Anick conjecture
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 609-629
-
- Article
- Export citation
Non-real zeros of real differential polynomials
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 631-639
-
- Article
- Export citation
Single-point blow-up for a doubly degenerate parabolic equation with nonlinear source
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 641-654
-
- Article
- Export citation
Families of curve congruences on Lorentzian surfaces and pencils of quadratic forms
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 655-672
-
- Article
- Export citation

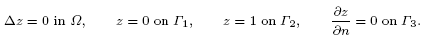
 ) for a compact Lie group
) for a compact Lie group 
 (
(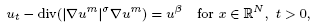
 on a smooth and oriented surface
on a smooth and oriented surface