Contents
Research Article
The Rothe method for the wave equation in several space dimensions
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-18
-
- Article
- Export citation
Compactness of bounded trajectories of dynamical systems in infinite dimensional spaces†
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 19-33
-
- Article
- Export citation
On diffracted wave fronts
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 35-54
-
- Article
- Export citation
Cohen elements in Banach algebras*†
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 55-70
-
- Article
- Export citation
Non-linear functional differential equations and abstract integral equations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 71-91
-
- Article
- Export citation
Some loci in S5 associated with systems of conics in a plane
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 93-107
-
- Article
- Export citation
Conics related by a pentagram: a problem of J. E. Reeve
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 109-115
-
- Article
- Export citation
Singular differential operators with spectra discrete and bounded below
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 117-134
-
- Article
- Export citation
The inverse scattering problem for a cylinder†
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 135-143
-
- Article
- Export citation
A multiplicity result for a class of elliptic boundary value problems
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 145-151
-
- Article
- Export citation
Effects of a sharp pressure rise on a compressible laminar boundary layer, when the Prandtl number is σ = 0.72*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 153-171
-
- Article
- Export citation
On the deficiency indices of a fourth order singular differential operator
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 173-176
-
- Article
- Export citation
Front matter
PRM volume 84 issue 1-2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 84 issue 1-2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation
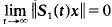 uniformly in bounded sets of
uniformly in bounded sets of 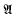 with a countable bounded approximate identity given by Esterle is modified slightly to be more analogous to the invertible elements in a unital Banach algebra. With the modified definition the
with a countable bounded approximate identity given by Esterle is modified slightly to be more analogous to the invertible elements in a unital Banach algebra. With the modified definition the 
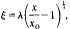 , andinvolve two parameters
, andinvolve two parameters