No CrossRef data available.
Article contents
XIX.—Asymptotic enumeration of connected graphs
Published online by Cambridge University Press: 14 February 2012
Synopsis
The number of different connected graphs (with some property P) on n labelled nodes with q edges is fnq. Again Fnq is the number of graphs on n labelled nodes with q edges, each of whose connected components has property P. We consider 8 types of graph for which 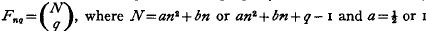 . We use a known relation between the generating functions of fnq and Fnq to find an asymptotic expansion of fnq in terms of binomial coefficients, valid if (q – ½n log n)/n→∞ as n→∞. This condition is also necessary for the existence of an asymptotic expansion of this kind.
. We use a known relation between the generating functions of fnq and Fnq to find an asymptotic expansion of fnq in terms of binomial coefficients, valid if (q – ½n log n)/n→∞ as n→∞. This condition is also necessary for the existence of an asymptotic expansion of this kind.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 68 , Issue 4 , 1970 , pp. 298 - 308
- Copyright
- Copyright © Royal Society of Edinburgh 1970
References
References to Literature
Erdös, P., and Rényi, A., 1959. “On random graphs I”, Publicationes Math., Debrecen, 6, 290–297.CrossRefGoogle Scholar
Erdös, P., 1960. “On the evolution of random graphs”, Magy. Tudom. Akad. Mat. Kut. Intéz. Közi., 5, 17–61.Google Scholar
Gilbert, E. N., 1956. “Enumeration of labelled graphs”, Can. J. Math., 8, 405–411.CrossRefGoogle Scholar

