Tilting subcategories with respect to cotorsion triples in abelian categories
Published online by Cambridge University Press: 28 June 2017
Extract
Given a non-negative integer n and a complete hereditary cotorsion triple 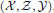 , the notion of
, the notion of 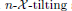 subcategories in an abelian category
subcategories in an abelian category 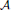 is introduced. It is proved that a virtually Gorenstein ring R is n-Gorenstein if and only if the subcategory
is introduced. It is proved that a virtually Gorenstein ring R is n-Gorenstein if and only if the subcategory 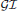 of Gorenstein injective R-modules is
of Gorenstein injective R-modules is 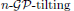 with respect to the cotorsion triple
with respect to the cotorsion triple 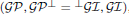 , where
, where 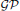 stands for the subcategory of Gorenstein projectives. In the case when a subcategory
stands for the subcategory of Gorenstein projectives. In the case when a subcategory 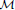 of
of 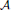 is closed under direct summands such that each object in
is closed under direct summands such that each object in 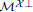 admits a right
admits a right 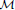 -approximation, a Bazzoni characterization is given for
-approximation, a Bazzoni characterization is given for 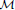 to be
to be 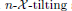 . Finally, an Auslander–Reiten correspondence is established between the class of
. Finally, an Auslander–Reiten correspondence is established between the class of 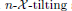 subcategories and that of certain subcategories of
subcategories and that of certain subcategories of 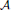 which are
which are 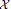 -coresolving covariantly finite and closed under direct summands.
-coresolving covariantly finite and closed under direct summands.
Keywords
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 147 , Issue 4 , August 2017 , pp. 703 - 726
- Copyright
- Copyright © Royal Society of Edinburgh 2017
- 3
- Cited by

