Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lin, Song-Sun
1993.
Symmetry-breakings for semilinear elliptic equations on finite cylindrical domains.
Proceedings of the American Mathematical Society,
Vol. 117,
Issue. 3,
p.
803.

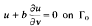 and
and 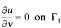 , where Ω
, where Ω