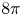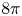1. Introduction
The Keller–Segel type equations describe chemotaxis, that is the movement of organisms (typically bacteria) in the presence of a (chemical) substance. The simplest Keller–Segel system is a pair of equations on the density of the organisms, $\varrho$![]() , and the concentration of the substance, $c$
, and the concentration of the substance, $c$![]() , both of which are functions on $[0,\, T) \times \mathbb {R}^{n}$
, both of which are functions on $[0,\, T) \times \mathbb {R}^{n}$![]() . Furthermore, $\varrho$
. Furthermore, $\varrho$![]() is assumed to be nonnegative and integrable. Together they satisfy the (parabolic-elliptic) Keller–Segel equations:
is assumed to be nonnegative and integrable. Together they satisfy the (parabolic-elliptic) Keller–Segel equations:
where $\operatorname {d\!}{}$![]() is the gradient, $\operatorname {d\!}{}^{*}$
is the gradient, $\operatorname {d\!}{}^{*}$![]() is its $L^{2}$
is its $L^{2}$![]() -dual (the divergence), and $\Delta = \operatorname {d\!}{}^{*} \operatorname {d\!}{}$
-dual (the divergence), and $\Delta = \operatorname {d\!}{}^{*} \operatorname {d\!}{}$![]() . The mass of $\varrho$
. The mass of $\varrho$![]() is
is
is a conserved quantity.
Stationary solutions to equations (1.1a) and (1.1b) satisfy
There is some ambiguity in the choice of $c$![]() in equations (1.2a) and (1.2b), and the standard choice is to use the Green's function of the Laplacian to eliminate $c$
in equations (1.2a) and (1.2b), and the standard choice is to use the Green's function of the Laplacian to eliminate $c$![]() and Eqn (1.2b) via
and Eqn (1.2b) via
and use the single equation
There is a well-known family of solutions to equation (1.3): Let $\lambda \in \mathbb {R}_+$![]() and $x_\star \in \mathbb {R}^{2}$
and $x_\star \in \mathbb {R}^{2}$![]() be arbitrary, and define
be arbitrary, and define
Then $\varrho _{\lambda, x_\star }$![]() is a solution to equation (1.3) with $m = 8 \pi$
is a solution to equation (1.3) with $m = 8 \pi$![]() .
.
When the metric is the standard, euclidean metric on $\mathbb {R}^{2}$![]() , the literature of equations (1.1a), (1.1b) and (1.3) is vast; the Reader may find good introductions in [Reference Blanchet, Dolbeault and Perthame2, Reference Dolbeault and Campos5, Reference Dolbeault and Perthame6]. Very little is known about the curved case, that is, when the underlying space is not the (flat) plane. We remark here the work of [Reference Maheux and Pierfelice8], where the authors considered equation (1.1a) and (1.1b) on the hyperbolic plane.
, the literature of equations (1.1a), (1.1b) and (1.3) is vast; the Reader may find good introductions in [Reference Blanchet, Dolbeault and Perthame2, Reference Dolbeault and Campos5, Reference Dolbeault and Perthame6]. Very little is known about the curved case, that is, when the underlying space is not the (flat) plane. We remark here the work of [Reference Maheux and Pierfelice8], where the authors considered equation (1.1a) and (1.1b) on the hyperbolic plane.
In this paper, we study the case when the metric is conformally equivalent to the flat metric and the conformal factor has the form $e^{2 \varphi }$![]() , where $\varphi$
, where $\varphi$![]() is smooth and compactly supported. Let us note that some of our results are novel already in the flat $(\varphi = 0)$
is smooth and compactly supported. Let us note that some of our results are novel already in the flat $(\varphi = 0)$![]() case. In particular, we prove that (under very mild hypotheses), solutions to equation (1.3) have mass $8 \pi$
case. In particular, we prove that (under very mild hypotheses), solutions to equation (1.3) have mass $8 \pi$![]() .
.
Outline of the paper
In $\mathbb {S}$![]() 2, we introduce the static Keller–Segel equation on the curved plane $( \mathbb {R}^{2},\, e^{2 \varphi } g_0 )$
2, we introduce the static Keller–Segel equation on the curved plane $( \mathbb {R}^{2},\, e^{2 \varphi } g_0 )$![]() . In $\mathbb {S}$
. In $\mathbb {S}$![]() 3, we prove in theorem 3.1 that, under mild hypothesis of the growth of $\varrho$
3, we prove in theorem 3.1 that, under mild hypothesis of the growth of $\varrho$![]() , the static Keller–Segel equation can be reduced to a simpler equation (see in equation (2.2)). Furthermore, in corollary 3.4, we give sharp bounds on the decay rate of $\varrho$
, the static Keller–Segel equation can be reduced to a simpler equation (see in equation (2.2)). Furthermore, in corollary 3.4, we give sharp bounds on the decay rate of $\varrho$![]() and in theorem 3.7 we show that a (nonzero) solution must have $m = 8 \pi$
and in theorem 3.7 we show that a (nonzero) solution must have $m = 8 \pi$![]() . In $\mathbb {S}$
. In $\mathbb {S}$![]() 4, we explore a connection between solutions to the (reduced) static Keller–Segel equation and Kazdan–Warner equation on the round sphere. As an application, we prove the nonexistence of solutions for certain conformal factors in theorem 4.2. Finally, in $\mathbb {S}$
4, we explore a connection between solutions to the (reduced) static Keller–Segel equation and Kazdan–Warner equation on the round sphere. As an application, we prove the nonexistence of solutions for certain conformal factors in theorem 4.2. Finally, in $\mathbb {S}$![]() 5.1, we prove the logarithmic Hardy–Littlewood–Sobolev for $( \mathbb {R}^{2},\, e^{2 \varphi } g_0 )$
5.1, we prove the logarithmic Hardy–Littlewood–Sobolev for $( \mathbb {R}^{2},\, e^{2 \varphi } g_0 )$![]() and in $\mathbb {S}$
and in $\mathbb {S}$![]() 5.2, as an application, we show that, as in the flat case, the Keller–Segel free energy on $( \mathbb {R}^{2},\, e^{2 \varphi } g_0 )$
5.2, as an application, we show that, as in the flat case, the Keller–Segel free energy on $( \mathbb {R}^{2},\, e^{2 \varphi } g_0 )$![]() is bounded from below only when $m = 8 \pi$
is bounded from below only when $m = 8 \pi$![]() .
.
2. The curved, static Keller–Segel equation
Let $g_0$![]() be the standard metric on $\mathbb {R}^{2}$
be the standard metric on $\mathbb {R}^{2}$![]() , let $\varphi \in C_\mathrm {cpt}^{\infty } ( \mathbb {R}^{2} )$
, let $\varphi \in C_\mathrm {cpt}^{\infty } ( \mathbb {R}^{2} )$![]() , let $g_\varphi := e^{2 \varphi } g_0$
, let $g_\varphi := e^{2 \varphi } g_0$![]() . Let $L_k^{p} ( \mathbb {R}^{2},\, g_\varphi )$
. Let $L_k^{p} ( \mathbb {R}^{2},\, g_\varphi )$![]() be Banach space of functions on $\mathbb {R}^{2}$
be Banach space of functions on $\mathbb {R}^{2}$![]() that are $L_k^{p}$
that are $L_k^{p}$![]() with respect to $g_\varphi$
with respect to $g_\varphi$![]() . Note that the properties of being bounded in $L_{1, \mathrm {loc}}^{2}$
. Note that the properties of being bounded in $L_{1, \mathrm {loc}}^{2}$![]() are independent of the chosen metric. Finally, let $L_+^{1} ( \mathbb {R}^{2},\, g_\varphi ) \subseteq L^{1} ( \mathbb {R}^{2},\, g_\varphi )$
are independent of the chosen metric. Finally, let $L_+^{1} ( \mathbb {R}^{2},\, g_\varphi ) \subseteq L^{1} ( \mathbb {R}^{2},\, g_\varphi )$![]() be the space of almost everywhere positive functions.
be the space of almost everywhere positive functions.
The area form and the Laplacian behave under a conformal change via
Thus the Green's function is conformally invariant:
For any $\varrho \in L_+^{1} ( \mathbb {R}^{2},\, g_\varphi )$![]() , let
, let
when the integral exists. Assume that the function $\varrho \in L_+^{1} ( \mathbb {R}^{2},\, g_\varphi ) \cap L_{1, \mathrm {loc}}^{2}$![]() is such that $c_{\varphi, \varrho }$
is such that $c_{\varphi, \varrho }$![]() is defined on $\mathbb {R}^{2}$
is defined on $\mathbb {R}^{2}$![]() . Then $\varrho$
. Then $\varrho$![]() is a solution to the static Keller–Segel equation on $( \mathbb {R}^{2},\, g_\varphi )$
is a solution to the static Keller–Segel equation on $( \mathbb {R}^{2},\, g_\varphi )$![]() if it solves (the weak version of)
if it solves (the weak version of)
In the next section we prove that, under mild hypotheses, equation (2.1) is equivalent to the simpler
We call equation (2.2) the reduced, static Keller–Segel equation.
In applications it is always assumed that $\varrho$![]() has finite mass. Furthermore, the minimal regularity needed for the weak version of equation (2.1) is $L_{1, \mathrm {loc}}^{2}$
has finite mass. Furthermore, the minimal regularity needed for the weak version of equation (2.1) is $L_{1, \mathrm {loc}}^{2}$![]() and the fact that $c_{\varphi, \varrho }$
and the fact that $c_{\varphi, \varrho }$![]() is defined. Finally, we impose the finiteness of the entropy: $\varrho \ln ( \varrho ) \in L^{1} ( \mathbb {R}^{2},\, g_\varphi )$
is defined. Finally, we impose the finiteness of the entropy: $\varrho \ln ( \varrho ) \in L^{1} ( \mathbb {R}^{2},\, g_\varphi )$![]() . This is implied by, for example, the finiteness of the Keller–Segel free energy; cf $\mathbb {S}$
. This is implied by, for example, the finiteness of the Keller–Segel free energy; cf $\mathbb {S}$![]() 5.2. With that in mind, we define the (curved) Keller–Segel configuration space as:
5.2. With that in mind, we define the (curved) Keller–Segel configuration space as:

Let $r (x) := |x|$![]() be the euclidean radial function. First we prove a bound on $c_{\varphi, \varrho }$
be the euclidean radial function. First we prove a bound on $c_{\varphi, \varrho }$![]() .
.
Lemma 2.1 Let $\varrho \in \mathcal {C}_\mathrm {KS} (m,\, \varphi )$![]() be a solution of the static Keller–Segel equation (2.1). Then the function $c_{\varphi, \varrho } + \tfrac {m}{4 \pi } \ln ( 1 + r^{2} )$
be a solution of the static Keller–Segel equation (2.1). Then the function $c_{\varphi, \varrho } + \tfrac {m}{4 \pi } \ln ( 1 + r^{2} )$![]() is bounded.
is bounded.
Proof. As $\Delta _\varphi c_{\varphi, \varrho } \in L^{1} ( B_1 (0),\, g_\varphi )$![]() , it is enough to prove, without any loss of generality, the boundedness of $c_{\varphi, \varrho } + \tfrac {m}{2 \pi } \ln ( r )$
, it is enough to prove, without any loss of generality, the boundedness of $c_{\varphi, \varrho } + \tfrac {m}{2 \pi } \ln ( r )$![]() , when $r \geqslant 1$
, when $r \geqslant 1$![]() .
.
Since $c_{\varphi, \varrho } (0) = - \tfrac {1}{2 \pi } \int _{\mathbb {R}^{2}} \varrho \ln (r) \: \mathrm {dA}_\varphi$![]() is finite, we have that
is finite, we have that
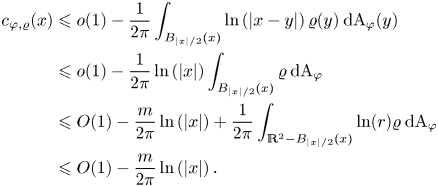
This proves the upper bound.
In order to get the lower bound, let us use Jensen's inequality to get

Since $\varrho \in L_{1, \mathrm {loc}}^{2}$![]() , we get that there exists $\delta > 0$
, we get that there exists $\delta > 0$![]() , such that for all $p > 1$
, such that for all $p > 1$![]() , $\varrho \in L^{p} ( B_\delta (0) )$
, $\varrho \in L^{p} ( B_\delta (0) )$![]() . We can assume that $\delta \leqslant 1$
. We can assume that $\delta \leqslant 1$![]() . Since for all $q \in [1,\, 2)$
. Since for all $q \in [1,\, 2)$![]() , $r^{- 1} \in L^{q} ( B_\delta (0) )$
, $r^{- 1} \in L^{q} ( B_\delta (0) )$![]() and $\tfrac {|x - y|}{|y|} \leqslant \tfrac {\sqrt {|x|^{2} + \delta ^{2}}}{\delta }$
and $\tfrac {|x - y|}{|y|} \leqslant \tfrac {\sqrt {|x|^{2} + \delta ^{2}}}{\delta }$![]() on $\mathbb {R}^{2} - B_\delta (0)$
on $\mathbb {R}^{2} - B_\delta (0)$![]() , we get that, for any $p > 1$
, we get that, for any $p > 1$![]() , that
, that

Thus, when $r \geqslant 1$![]() , we get that
, we get that
which completes the proof.
3. Reduction of order and the necessity of $m = 8 \pi$
Theorem 3.1 Let $\varrho \in \mathcal {C}_\mathrm {KS} (m,\, \varphi )$![]() be a solution of the static Keller–Segel equation (2.1). Furthermore assume the following bound: there exists a positive number $C,$
be a solution of the static Keller–Segel equation (2.1). Furthermore assume the following bound: there exists a positive number $C,$![]() such that on $\mathbb {R}^{2} - B_C (0),$
such that on $\mathbb {R}^{2} - B_C (0),$![]() we have
we have
Then the reduced, static Keller–Segel equation (2.2) holds, that is $\operatorname {d\!}{} ( \ln ( \varrho ) - c_{\varphi, \varrho } ) = 0$![]() .
.
Remark 3.2 If $\varrho \in L^{\infty } ( \mathbb {R}^{2} )$![]() , then equation (3.1) is trivially satisfied with $C = \max ( 1,\, \| \varrho \|_{L^{\infty } ( \mathbb {R}^{2} )} )$
, then equation (3.1) is trivially satisfied with $C = \max ( 1,\, \| \varrho \|_{L^{\infty } ( \mathbb {R}^{2} )} )$![]() . We conjecture that equation (3.1) is not necessary in general for the conclusion theorem 3.1 to hold.
. We conjecture that equation (3.1) is not necessary in general for the conclusion theorem 3.1 to hold.
Remark 3.3 A corollary of the reduced, static Keller–Segel equation (2.2) is that the (nonreduced) static Keller–Segel equation (2.1) is no longer nonlocal, as $c_{\varrho, \varphi }$![]() can be eliminated using $\operatorname {d\!}{} c_{\varphi, \varrho } = \operatorname {d\!}{} ( \ln ( \varrho ) ) = \tfrac {\operatorname {d\!}{} \varrho }{\varrho }$
can be eliminated using $\operatorname {d\!}{} c_{\varphi, \varrho } = \operatorname {d\!}{} ( \ln ( \varrho ) ) = \tfrac {\operatorname {d\!}{} \varrho }{\varrho }$![]() , and get
, and get
Thus the static Keller–Segel equation (2.1) becomes
Proof of theorem 3.1. Let $f := \ln ( \varrho ) - c_{\varphi, \varrho }$![]() . The static Keller–Segel equation (2.1) implies that
. The static Keller–Segel equation (2.1) implies that
We now apply an Agmon-trick type argument: Let $\chi$![]() be a smooth and compactly supported function. Then, using $\phi = f \chi ^{2}$
be a smooth and compactly supported function. Then, using $\phi = f \chi ^{2}$![]() in the second row, we get
in the second row, we get

Now for each $R \gg 1$![]() , let $\chi = \chi _R$
, let $\chi = \chi _R$![]() be a smooth cut-off function that is 1 on $B_R (0)$
be a smooth cut-off function that is 1 on $B_R (0)$![]() , vanishes on $\mathbb {R}^{2} - B_{2 R} (0)$
, vanishes on $\mathbb {R}^{2} - B_{2 R} (0)$![]() , and (for some $K \in \mathbb {R}_+$
, and (for some $K \in \mathbb {R}_+$![]() ) $|\operatorname {d\!}{} \chi _R| = \tfrac {K}{R}$
) $|\operatorname {d\!}{} \chi _R| = \tfrac {K}{R}$![]() . Let $A_R = B_{2 R} (0) - B_R (0)$
. Let $A_R = B_{2 R} (0) - B_R (0)$![]() . Then we get that
. Then we get that

To complete the proof, we show now that the last limit inferior is zero. Since

it is enough to show that both terms under the square roots are $o ( R^{2} )$![]() , at least for some divergent sequence of radii. This is immediate for the second term by lemma 2.1. To bound the first term, let $C$
, at least for some divergent sequence of radii. This is immediate for the second term by lemma 2.1. To bound the first term, let $C$![]() be the constant from equation (3.1) and break up $A_R$
be the constant from equation (3.1) and break up $A_R$![]() into 2 pieces:
into 2 pieces:

By equation (3.1), $A_R = A_{R, I} \cup A_{R, II}$![]() . Let us first inspect
. Let us first inspect

Finally, note that on $A_{R, II}$![]() , we have $\left | \ln ( \varrho ) \right | = O ( R^{2} \ln (R) )$
, we have $\left | \ln ( \varrho ) \right | = O ( R^{2} \ln (R) )$![]() . Thus, for $R \gg 1$
. Thus, for $R \gg 1$![]() , we have
, we have

Now let $R_k := 2^{k}$![]() , and then
, and then
Since $\varrho \ln ( \varrho ) \in L^{1} ( \mathbb {R}^{2},\, g_0 )$![]() we have that
we have that

and thus

and hence
which implies equation (2.2), and thus completes the proof.
Corollary 3.4 If $\varrho \in \mathcal {C}_\mathrm {KS}$![]() is a solution of the static Keller–Segel equation (2.1) and satisfies (3.1), then there is a number $K = K (\varphi,\, \varrho ) \geqslant 1$
is a solution of the static Keller–Segel equation (2.1) and satisfies (3.1), then there is a number $K = K (\varphi,\, \varrho ) \geqslant 1$![]() such that
such that
In particular, $\varrho \sim r^{- \frac {m}{2 \pi }}$![]() and $m > 4 \pi$
and $m > 4 \pi$![]() .
.
Proof. We have

which concludes the proof.
Remark 3.5 Theorem 3.1 remains true (with the same proof) even when $g_\varphi$![]() is replaced by any compactly supported, smooth perturbation of $g_0$
is replaced by any compactly supported, smooth perturbation of $g_0$![]() . However proving lemma 2.1 becomes more complicated in that case, although conjecturally, that claim should still hold, and thus so should corollary 3.4.
. However proving lemma 2.1 becomes more complicated in that case, although conjecturally, that claim should still hold, and thus so should corollary 3.4.
Remark 3.6 Before stating our next theorem, let us recall a few facts, commonly used in literature of the Keller–Segel equations.
First of all, and to the best of our knowledge, the only known solutions in the flat case are the ones given in equation (1.4). Note that they all have mass $8 \pi$![]() .
.
A complementary fact, supporting the conjecture that static solutions must have mass $8 \pi$![]() , is the the following ‘Virial Theorem’ that applies to the time-dependent equation as well: Assume that $\varrho$
, is the the following ‘Virial Theorem’ that applies to the time-dependent equation as well: Assume that $\varrho$![]() is a solution to the (time-dependent) Keller–Segel equation (1.1a) and (1.1b), such that for all $t$
is a solution to the (time-dependent) Keller–Segel equation (1.1a) and (1.1b), such that for all $t$![]() in the domain of $\varrho$
in the domain of $\varrho$![]() the following quantity is finite
the following quantity is finite
Then $W$![]() satisfies the following equation (cf. [Reference Blanchet, Dolbeault and Perthame2]*lemma 22 for the proof):
satisfies the following equation (cf. [Reference Blanchet, Dolbeault and Perthame2]*lemma 22 for the proof):
In particular, if $\varrho$![]() is a (positive) solution to the static Keller–Segel equation (2.1) with finite $W$
is a (positive) solution to the static Keller–Segel equation (2.1) with finite $W$![]() , then $m = 8 \pi$
, then $m = 8 \pi$![]() . Note that for each $\varrho _{\lambda, x_\star }$
. Note that for each $\varrho _{\lambda, x_\star }$![]() in equation (1.4), we get $W = \infty$
in equation (1.4), we get $W = \infty$![]() , so the above two results are indeed complementary.
, so the above two results are indeed complementary.
In the next theorem we prove that, under equation (3.1), all (positive) solutions to the static Keller–Segel equation (2.1) must have mass $8 \pi$![]() .
.
Theorem 3.7 If $\varrho \in \mathcal {C}_\mathrm {KS}$![]() is a solution of the static Keller–Segel equation (2.1) and satisfies equation (3.1), then its mass is necessarily $8 \pi$
is a solution of the static Keller–Segel equation (2.1) and satisfies equation (3.1), then its mass is necessarily $8 \pi$![]() .
.
Proof. By corollary 3.4, we have that $m > 4 \pi$![]() and thus, for some $\epsilon > 0$
and thus, for some $\epsilon > 0$![]() , we have $\varrho = O ( r^{- 2 - \epsilon } )$
, we have $\varrho = O ( r^{- 2 - \epsilon } )$![]() .
.
Let now $v = (v_1,\, v_2)$![]() be a smooth, compactly supported vector field. Let us pair both sides of equation (2.2) with $- \varrho v$
be a smooth, compactly supported vector field. Let us pair both sides of equation (2.2) with $- \varrho v$![]() , integrate over $\mathbb {R}^{2}$
, integrate over $\mathbb {R}^{2}$![]() with respect to $\: \mathrm {dA}_0$
with respect to $\: \mathrm {dA}_0$![]() and then integrate by parts in the first term to get
and then integrate by parts in the first term to get

For any smooth, real function $f$![]() , let
, let
and let $\chi _R$![]() as in the proof of theorem 3.1. Let us assume that $\left | \operatorname {d\!}{} f \right | \in L^{2} ( \mathbb {R}^{2},\, g_\varphi )$
as in the proof of theorem 3.1. Let us assume that $\left | \operatorname {d\!}{} f \right | \in L^{2} ( \mathbb {R}^{2},\, g_\varphi )$![]() . Then for $v = \chi _R v^{f}$
. Then for $v = \chi _R v^{f}$![]() equation (3.3) becomes
equation (3.3) becomes

As $R \rightarrow \infty$![]() the last term goes to zero, by definition, $\mathcal {I}_1 (R) \rightarrow m$
the last term goes to zero, by definition, $\mathcal {I}_1 (R) \rightarrow m$![]() . Using equation (2), we get
. Using equation (2), we get

thus

Finally, if we can choose a smooth $f$![]() so that
so that
and $|\operatorname {d\!}{} f| \in L^{2} ( \mathbb {R}^{2},\, g_\varphi )$![]() , then $\mathcal {I}_3 (R) = 0$
, then $\mathcal {I}_3 (R) = 0$![]() , for all $R$
, for all $R$![]() . For any smooth, compactly supported function $\phi$
. For any smooth, compactly supported function $\phi$![]() , let
, let
and let $( \mathcal {H}_{\varphi, \varrho },\, \langle - | - \rangle _{\varphi, \varrho } )$![]() the corresponding Hilbert space. Clearly $\mathcal {H}_{\varphi, \varrho } \subseteq L_{1, \mathrm {loc}}^{2}$
the corresponding Hilbert space. Clearly $\mathcal {H}_{\varphi, \varrho } \subseteq L_{1, \mathrm {loc}}^{2}$![]() . The weak formulation of equation (3.5) on $\mathcal {H}_{\varphi, \varrho }$
. The weak formulation of equation (3.5) on $\mathcal {H}_{\varphi, \varrho }$![]() is
is

Now if $f = \phi \in C_{\mathrm {cpt}}^{\infty } ( \mathbb {R}^{2} )$![]() , then
, then

and, using that $\varphi$![]() has compact support and equation (3.2), we have
has compact support and equation (3.2), we have

Thus the conditions of the Lax–Milgram theorem are satisfied and hence there is a unique $f \in \mathcal {H}_{\varphi, \varrho }$![]() that solves equation (3.5). By elliptic regularity, $f$
that solves equation (3.5). By elliptic regularity, $f$![]() is in fact smooth and by the definition $\mathcal {H}_{\varphi, \varrho }$
is in fact smooth and by the definition $\mathcal {H}_{\varphi, \varrho }$![]() , $|\operatorname {d\!}{} f| \in L^{2} ( \mathbb {R}^{2},\, g_\varphi )$
, $|\operatorname {d\!}{} f| \in L^{2} ( \mathbb {R}^{2},\, g_\varphi )$![]() . Hence equation (3.4) becomes $0 = 4\,m - \tfrac {m^{2}}{2 \pi }$
. Hence equation (3.4) becomes $0 = 4\,m - \tfrac {m^{2}}{2 \pi }$![]() , which concludes the proof.
, which concludes the proof.
4. Connection to the critical Kazdan–Warner equation on the round sphere
Let us assume that $\varrho \in \mathcal {C}_\mathrm {KS}$![]() is a solution of the static Keller–Segel equation (2.1) and satisfies equation (3.1), and thus $m = 8 \pi$
is a solution of the static Keller–Segel equation (2.1) and satisfies equation (3.1), and thus $m = 8 \pi$![]() . Fix $\lambda \in \mathbb {R}_+$
. Fix $\lambda \in \mathbb {R}_+$![]() and $x_\star \in \mathbb {R}^{2}$
and $x_\star \in \mathbb {R}^{2}$![]() , and let $\varrho _{\lambda, x_\star }$
, and let $\varrho _{\lambda, x_\star }$![]() as in equation (1.4). Pick the unique stereographic projection $p_{\lambda, x_\star } : \mathbb {S}^{2} - \{ \mbox { North pole } \} \rightarrow \mathbb {R}^{2}$
as in equation (1.4). Pick the unique stereographic projection $p_{\lambda, x_\star } : \mathbb {S}^{2} - \{ \mbox { North pole } \} \rightarrow \mathbb {R}^{2}$![]() , so that $g_{\mathbb {S}^{2}} := ( p_{\lambda, x_\star } )^{*} ( \tfrac {1}{2} \varrho _{\lambda, x_\star } g_0 )$
, so that $g_{\mathbb {S}^{2}} := ( p_{\lambda, x_\star } )^{*} ( \tfrac {1}{2} \varrho _{\lambda, x_\star } g_0 )$![]() is the round metric of unit radius. By corollary 3.4, the function $\widetilde {u} := \tfrac {1}{2} \ln ( \tfrac {\varrho }{\varrho _{\lambda, x_\star }} )$
is the round metric of unit radius. By corollary 3.4, the function $\widetilde {u} := \tfrac {1}{2} \ln ( \tfrac {\varrho }{\varrho _{\lambda, x_\star }} )$![]() is bounded on $\mathbb {R}^{2}$
is bounded on $\mathbb {R}^{2}$![]() . Let $u := \widetilde {u} \circ p_{\lambda, x_\star } \in L^{\infty } ( \mathbb {S}^{2} )$
. Let $u := \widetilde {u} \circ p_{\lambda, x_\star } \in L^{\infty } ( \mathbb {S}^{2} )$![]() . Then (omitting obvious pullbacks and computations) we have
. Then (omitting obvious pullbacks and computations) we have

Since $\varphi$![]() is compactly supported, the pullback of $e^{2 \varphi }$
is compactly supported, the pullback of $e^{2 \varphi }$![]() to $\mathbb {S}^{2}$
to $\mathbb {S}^{2}$![]() via $p_{\lambda, x_\star }$
via $p_{\lambda, x_\star }$![]() extends smoothly over the North pole. Let us denote this extension by $h$
extends smoothly over the North pole. Let us denote this extension by $h$![]() . Then the equation on $u$
. Then the equation on $u$![]() becomes
becomes
This is the equation of Kazdan and Warner, [Reference Kazdan and Warner7]*equation (1.3), with $k = 1$![]() (note that they use the opposite sign convention for the Laplacian). When $\varphi$
(note that they use the opposite sign convention for the Laplacian). When $\varphi$![]() vanishes identically, then $u = 0$
vanishes identically, then $u = 0$![]() is a solution, which corresponds to the well-known $\varrho = \varrho _{\lambda, x_\star }$
is a solution, which corresponds to the well-known $\varrho = \varrho _{\lambda, x_\star }$![]() solution on the flat plane. More generally, given any $\lambda \in \mathbb {R}_+$
solution on the flat plane. More generally, given any $\lambda \in \mathbb {R}_+$![]() and $x_\star \in \mathbb {R}^{2}$
and $x_\star \in \mathbb {R}^{2}$![]() and any positive scalar curvature metric $g$
and any positive scalar curvature metric $g$![]() on $\mathbb {S}^{2}$
on $\mathbb {S}^{2}$![]() , one can construct a solution to curved, static Keller–Segel equation (2.1) as follows: by the uniformization theorem, $g$
, one can construct a solution to curved, static Keller–Segel equation (2.1) as follows: by the uniformization theorem, $g$![]() and $g_{\mathbb {S}^{2}}$
and $g_{\mathbb {S}^{2}}$![]() are always conformally equivalent. Thus we have a function, $u$
are always conformally equivalent. Thus we have a function, $u$![]() , that solves equation (4.1) with $h$
, that solves equation (4.1) with $h$![]() being the scalar curvature of $g$
being the scalar curvature of $g$![]() (pulled back under a diffeomorphism). Let now $\widetilde {u}$
(pulled back under a diffeomorphism). Let now $\widetilde {u}$![]() and $\widetilde {h}$
and $\widetilde {h}$![]() be the pushforwards of $u$
be the pushforwards of $u$![]() and $h$
and $h$![]() , respectively, to $\mathbb {R}^{2}$
, respectively, to $\mathbb {R}^{2}$![]() via $p_{\lambda, x_\star }$
via $p_{\lambda, x_\star }$![]() , and let $\varrho := \varrho _{\lambda, x_\star } e^{2 \widetilde {u}}$
, and let $\varrho := \varrho _{\lambda, x_\star } e^{2 \widetilde {u}}$![]() . Then $\varrho$
. Then $\varrho$![]() solves the curved, static Keller–Segel equation (2.1) with $\varphi = \tfrac {1}{2} \ln ( \widetilde {h} )$
solves the curved, static Keller–Segel equation (2.1) with $\varphi = \tfrac {1}{2} \ln ( \widetilde {h} )$![]() .
.
Remark 4.1 Using the reduced, static Keller–Segel equation (2.2) also, equations similar to the Kazdan–Warner equation (4.1) were studied in [Reference Bonheure, Casteras and Noris3, Reference Wang, Wang and Yang9]. These equations however are still on the plane so the geometric interpretation above is lost.
Unfortunately, equation (4.1) is the critical version of the Kazdan–Warner equation in [Reference Kazdan and Warner7]. Thus we cannot, in general, assume solvability for an arbitrary $h$![]() . In fact, Kazdan and Warner found a necessary condition for the existence of solutions: For each spherical harmonic of degree one, $u_1$
. In fact, Kazdan and Warner found a necessary condition for the existence of solutions: For each spherical harmonic of degree one, $u_1$![]() , by [Reference Kazdan and Warner7]*equation (8.10), we have
, by [Reference Kazdan and Warner7]*equation (8.10), we have
where $\omega _{\mathbb {S}^{2}}$![]() is the symplectic/area form of $g_{\mathbb {S}^{2}}$
is the symplectic/area form of $g_{\mathbb {S}^{2}}$![]() . We use equation (4.2) to prove the following:
. We use equation (4.2) to prove the following:
Theorem 4.2 There exists $\varphi \in C_\mathrm {cpt}^{\infty } ( \mathbb {R}^{2} )$![]() , arbitrarily close to the identically zero function, such that the static Keller–Segel equation (2.1) has no solutions satisfying equation (3.1).
, arbitrarily close to the identically zero function, such that the static Keller–Segel equation (2.1) has no solutions satisfying equation (3.1).
Proof. Let us assume that $\varphi$![]() is radial (with respect to $x_\star$
is radial (with respect to $x_\star$![]() ). Then $h$
). Then $h$![]() is only a function of the polar angle $\theta \in ( - \tfrac {\pi }{2},\, \tfrac {\pi }{2} )$
is only a function of the polar angle $\theta \in ( - \tfrac {\pi }{2},\, \tfrac {\pi }{2} )$![]() , on $\mathbb {S}^{2}$
, on $\mathbb {S}^{2}$![]() . When $u_1 = \sin ( \theta )$
. When $u_1 = \sin ( \theta )$![]() , then equation (4.2) becomes
, then equation (4.2) becomes
Since $\partial _\theta h \sim e^{2 \varphi } \partial _r \varphi$![]() , we get that if $\varphi$
, we get that if $\varphi$![]() is nonconstant and $\partial _r \varphi$
is nonconstant and $\partial _r \varphi$![]() is either nonnegative or nonpositive, then equation (4.3) cannot hold. This concludes the proof.
is either nonnegative or nonpositive, then equation (4.3) cannot hold. This concludes the proof.
5. The variation aspects of the Keller–Segel theory on curved planes
We end this paper with a complementary result to theorem 3.7, showing that the energy functional (formally) corresponding to the Keller–Segel flow in equation (1.1a) and (1.1b) is bounded from below only when $m = 8 \pi$![]() . In order to do that, we first prove a curved version of the logarithmic Hardy–Littlewood–Sobolev inequality.
. In order to do that, we first prove a curved version of the logarithmic Hardy–Littlewood–Sobolev inequality.
5.1 Curved logarithmic Hardy–Littlewood–Sobolev inequality and the Keller–Segel free energy
Let $\lambda \in \mathbb {R}_+$![]() and $x_\star \in \mathbb {R}^{2}$
and $x_\star \in \mathbb {R}^{2}$![]() , and define
, and define
Then $\mu _{\lambda, x_\star }$![]() is everywhere positive, $\int _{\mathbb {R}^{2}} \mu _{\lambda, x_\star } \: \mathrm {dA}_0 = 1$
is everywhere positive, $\int _{\mathbb {R}^{2}} \mu _{\lambda, x_\star } \: \mathrm {dA}_0 = 1$![]() , and for any $f \in C_{\mathrm {cpt}}^{\infty } ( \mathbb {R}^{2} )$
, and for any $f \in C_{\mathrm {cpt}}^{\infty } ( \mathbb {R}^{2} )$![]()
The following identities about $\mu _{\lambda, x_\star }$![]() are easy to verify:
are easy to verify:

Now we can state the logarithmic Hardy–Littlewood–Sobolev inequality on $( \mathbb {R}^{2},\, g_0 )$![]() , which is a special case of [Reference Beckner1]*theorem 2.
, which is a special case of [Reference Beckner1]*theorem 2.
Theorem 5.1 Let $\varrho$![]() be an almost everywhere positive function on $\mathbb {R}^{2}$
be an almost everywhere positive function on $\mathbb {R}^{2}$![]() and assume that
and assume that
Then for all $\lambda \in \mathbb {R}_+,$![]() $x_\star \in \mathbb {R}^{2},$
$x_\star \in \mathbb {R}^{2},$![]() we have
we have

Moreover, equality holds exactly when $\varrho = m \mu _{\lambda, x_\star }$![]() .
.
Idea of the proof: Note that equations (5.3a), (5.3c), and (5.3a) imply that equation (5.4) is equivalent to

Now equation (5.5) is the $n = 2$![]() and $f = g$
and $f = g$![]() case of [Reference Beckner1]*inequality (27).
case of [Reference Beckner1]*inequality (27).
Let now $g$![]() be any smooth Riemannian metric on $\mathbb {R}^{2}$
be any smooth Riemannian metric on $\mathbb {R}^{2}$![]() , not necessarily conformally equivalent to $g_0$
, not necessarily conformally equivalent to $g_0$![]() . There still exists a smooth function, $\varphi$
. There still exists a smooth function, $\varphi$![]() , such that if the area form of $g$
, such that if the area form of $g$![]() is $\: \mathrm {dA}_g$
is $\: \mathrm {dA}_g$![]() , then
, then
For the remainder of this section (but this section only), let $\varphi$![]() be defined via equation (5.6), and write, as before $\: \mathrm {dA}_\varphi := \: \mathrm {dA}_g$
be defined via equation (5.6), and write, as before $\: \mathrm {dA}_\varphi := \: \mathrm {dA}_g$![]() . When $g$
. When $g$![]() is not conformally equivalent to $g_0$
is not conformally equivalent to $g_0$![]() , then $G$
, then $G$![]() is no longer the Green's function for $g$
is no longer the Green's function for $g$![]() . Now let $\mu _{\lambda, x_\star }^{\varphi } := \mu _{\lambda, x_\star } e^{- 2 \varphi }$
. Now let $\mu _{\lambda, x_\star }^{\varphi } := \mu _{\lambda, x_\star } e^{- 2 \varphi }$![]() . Note that $\int _{\mathbb {R}^{2}} \mu _{\lambda, x_\star }^{\varphi } \: \mathrm {dA}_\varphi = 1$
. Note that $\int _{\mathbb {R}^{2}} \mu _{\lambda, x_\star }^{\varphi } \: \mathrm {dA}_\varphi = 1$![]() .
.
The next lemma is a generalization of theorem 5.1.
Lemma 5.2 Let $\varrho$![]() be an almost everywhere positive function on $\mathbb {R}^{2}$
be an almost everywhere positive function on $\mathbb {R}^{2}$![]() and assume that
and assume that
Then for all $\lambda \in \mathbb {R}_+$![]() and $x_\star \in \mathbb {R}^{2},$
and $x_\star \in \mathbb {R}^{2},$![]() we have
we have

and equality holds exactly when $\varrho = m \mu _{\lambda, x_\star }^{\varphi }$![]() .
.
Proof. Let us first rewrite the left-hand side of equation (5.7):

Since $\varrho e^{2 \varphi }$![]() is almost everywhere positive and
is almost everywhere positive and
we can use equation (5.4), with $\varrho$![]() replaced by $\varrho e^{2 \varphi }$
replaced by $\varrho e^{2 \varphi }$![]() , and get
, and get

Furthermore

Combining equations (5.8), (5.9), and (5.10) proves equation (5.7). Finally, equality in equation (5.9) holds exactly when $\varrho e^{2 \varphi } = m \mu$![]() , or equivalently, when $\varrho = m \mu _{\lambda, x_\star }^{\varphi }$
, or equivalently, when $\varrho = m \mu _{\lambda, x_\star }^{\varphi }$![]() , which conclude the proof.
, which conclude the proof.
Remark 5.3 As opposed to the flat case, when $\varphi$![]() is not identically zero, the $m = 8 \pi$
is not identically zero, the $m = 8 \pi$![]() minimizer for the curved logarithmic Hardy–Littlewood–Sobolev equation (5.7), $8 \pi \mu _{\lambda, x_\star }^{\varphi }$
minimizer for the curved logarithmic Hardy–Littlewood–Sobolev equation (5.7), $8 \pi \mu _{\lambda, x_\star }^{\varphi }$![]() , is not a solution to the static Keller–Segel equation (2.1), nor the reduced, static Keller–Segel equation (2.2). Instead, we get
, is not a solution to the static Keller–Segel equation (2.1), nor the reduced, static Keller–Segel equation (2.2). Instead, we get
5.2 The Keller–Segel free energy
The (flat) Keller–Segel free energy of $\varrho \in \mathcal {C}_\mathrm {KS} (m,\, 0)$![]() is
is

Remark 5.4 Formally, equation (1.1a) is the negative gradient flow of the Keller–Segel free energy under the Wasserstein metric. Formally this metric can be introduced as follows: If $\varrho \in \mathcal {C}_\mathrm {KS} (m,\, \varphi )$![]() , then the operator $f \mapsto L_\varrho (f) := \operatorname {d\!}{}^{*} ( \varrho \operatorname {d\!}{} f )$
, then the operator $f \mapsto L_\varrho (f) := \operatorname {d\!}{}^{*} ( \varrho \operatorname {d\!}{} f )$![]() is expected to be nondegenerate. Then if $\dot {\varrho }$
is expected to be nondegenerate. Then if $\dot {\varrho }$![]() is a tangent vector to $\mathcal {C}_\mathrm {KS} (m,\, \varphi )$
is a tangent vector to $\mathcal {C}_\mathrm {KS} (m,\, \varphi )$![]() , then its Wasserstein norm is given by
, then its Wasserstein norm is given by
Then the Wasserstein norm is a Hilbert norm, thus can be used to define gradient flows.
Remark 5.5 The functional in (5.11) is also the energy of self-gravitating Brownian dust; cf. [Reference Chavanis, Ribot, Rosier and Sire4].
Let us generalize $\mathcal {F}_0$![]() to $( \mathbb {R}^{2},\, g_\varphi )$
to $( \mathbb {R}^{2},\, g_\varphi )$![]() : For any $\varrho \in \mathcal {C}_\mathrm {KS} (m,\, \varphi )$
: For any $\varrho \in \mathcal {C}_\mathrm {KS} (m,\, \varphi )$![]() , let the curved Keller–Segel free energy be
, let the curved Keller–Segel free energy be

Now we are ready to prove our last main result.
Theorem 5.6 The curved Keller–Segel free energy (5.12) is bounded from below on $\mathcal {C}_\mathrm {KS} (m,\, \varphi ),$![]() exactly when $m = 8 \pi$
exactly when $m = 8 \pi$![]() .
.
Proof. Let $m,\, \lambda \in \mathbb {R}_+$![]() , and $\mu _{\lambda, 0}$
, and $\mu _{\lambda, 0}$![]() as in equation (5.1) (with $x_\star = 0$
as in equation (5.1) (with $x_\star = 0$![]() ). Now equations (5.3c) and (5.3a) imply that
). Now equations (5.3c) and (5.3a) imply that

As $\lambda \rightarrow 0^{+}$![]() , the last term goes to $\varphi (x_\star )$
, the last term goes to $\varphi (x_\star )$![]() . Thus, when $m > 8 \pi$
. Thus, when $m > 8 \pi$![]() , then
, then
Similarly, as $\lambda \rightarrow \infty$![]() , the last term goes to zero. Thus, when $m < 8 \pi$
, the last term goes to zero. Thus, when $m < 8 \pi$![]() , then
, then
This proves the claim for $m \neq 8 \pi$![]() .
.
When $m = 8 \pi$![]() , then for any $\varrho \in \mathcal {C}_\mathrm {KS} (m,\, \varphi )$
, then for any $\varrho \in \mathcal {C}_\mathrm {KS} (m,\, \varphi )$![]() , we have
, we have

Now, using equations (5.7), (5.3b), (5.3c), and (5.2), and plugging back $m = 8 \pi$![]() , we get
, we get
which completes the proof.
Remark 5.7 It is not entirely obvious if the relevant generalization of Keller–Segel free energy (5.11) is the functional, $\mathcal {F}_\varphi$![]() , in equation (5.12). There is an generalization that is minimally coupled to the metric: Let $\kappa _\varphi := \Delta _\varphi \varphi$
, in equation (5.12). There is an generalization that is minimally coupled to the metric: Let $\kappa _\varphi := \Delta _\varphi \varphi$![]() be the Gauss curvature of $g_\varphi$
be the Gauss curvature of $g_\varphi$![]() and $q \in \mathbb {R}$
and $q \in \mathbb {R}$![]() be a coupling constant. Then let us define
be a coupling constant. Then let us define

When $m \neq 8 \pi$![]() , the proof of theorem 5.6 can still be used to prove the unboundedness of $\mathcal {F}_{\varphi, q}$
, the proof of theorem 5.6 can still be used to prove the unboundedness of $\mathcal {F}_{\varphi, q}$![]() , and when $m = 8 \pi$
, and when $m = 8 \pi$![]() , we get
, we get

In particular, when $q = 2$![]() , then $\varrho = 8 \pi \mu _{\lambda, x_\star }^{\varphi }$
, then $\varrho = 8 \pi \mu _{\lambda, x_\star }^{\varphi }$![]() is an absolute minimizer of $\mathcal {F}_{\varphi, q}$
is an absolute minimizer of $\mathcal {F}_{\varphi, q}$![]() .
.
Acknowledgments
I thank Michael Sigal for introducing me to the topic and for his initial guidance. I also thank the referee for their helpful recommendations.