No CrossRef data available.
Article contents
The space of commuting elements in a Lie group and maps between classifying spaces
Published online by Cambridge University Press: 27 October 2023
Abstract
Let $\pi$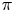 be a discrete group, and let $G$
be a discrete group, and let $G$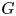 be a compact-connected Lie group. Then, there is a map $\Theta \colon \mathrm {Hom}(\pi,G)_0\to \mathrm {map}_*(B\pi,BG)_0$
be a compact-connected Lie group. Then, there is a map $\Theta \colon \mathrm {Hom}(\pi,G)_0\to \mathrm {map}_*(B\pi,BG)_0$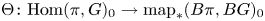 between the null components of the spaces of homomorphisms and based maps, which sends a homomorphism to the induced map between classifying spaces. Atiyah and Bott studied this map for $\pi$
between the null components of the spaces of homomorphisms and based maps, which sends a homomorphism to the induced map between classifying spaces. Atiyah and Bott studied this map for $\pi$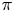 a surface group, and showed that it is surjective in rational cohomology. In this paper, we prove that the map $\Theta$
a surface group, and showed that it is surjective in rational cohomology. In this paper, we prove that the map $\Theta$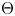 is surjective in rational cohomology for $\pi =\mathbb {Z}^m$
is surjective in rational cohomology for $\pi =\mathbb {Z}^m$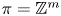 and the classical group $G$
and the classical group $G$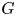 except for $SO(2n)$
except for $SO(2n)$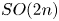 , and that it is not surjective for $\pi =\mathbb {Z}^m$
, and that it is not surjective for $\pi =\mathbb {Z}^m$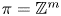 with $m\ge 3$
with $m\ge 3$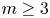 and $G=SO(2n)$
and $G=SO(2n)$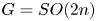 with $n\ge 4$
with $n\ge 4$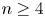 . As an application, we consider the surjectivity of the map $\Theta$
. As an application, we consider the surjectivity of the map $\Theta$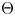 in rational cohomology for $\pi$
in rational cohomology for $\pi$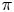 a finitely generated nilpotent group. We also consider the dimension of the cokernel of the map $\Theta$
a finitely generated nilpotent group. We also consider the dimension of the cokernel of the map $\Theta$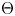 in rational homotopy groups for $\pi =\mathbb {Z}^m$
in rational homotopy groups for $\pi =\mathbb {Z}^m$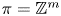 and the classical groups $G$
and the classical groups $G$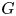 except for $SO(2n)$
except for $SO(2n)$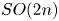 .
.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 155 , Issue 3 , June 2025 , pp. 735 - 755
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh


