No CrossRef data available.
Article contents
Series expansion of Leray–Trudinger inequality
Published online by Cambridge University Press: 20 December 2021
Abstract
In this paper, we establish an infinite series expansion of Leray–Trudinger inequality, which is closely related with Hardy inequality and Moser Trudinger inequality. Our result extends early results obtained by Mallick and Tintarev [A. Mallick and C. Tintarev. An improved Leray-Trudinger inequality. Commun. Contemp. Math. 20 (2018), 17501034. OP 21] to the case with many logs. It should be pointed out that our result is about series expansion of Hardy inequality under the case $p=n$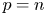 , which case is not considered by Gkikas and Psaradakis in [K. T. Gkikas and G. Psaradakis. Optimal non-homogeneous improvements for the series expansion of Hardy's inequality. Commun. Contemp. Math. doi:10.1142/S0219199721500310]. However, we can't obtain the optimal form by our method.
, which case is not considered by Gkikas and Psaradakis in [K. T. Gkikas and G. Psaradakis. Optimal non-homogeneous improvements for the series expansion of Hardy's inequality. Commun. Contemp. Math. doi:10.1142/S0219199721500310]. However, we can't obtain the optimal form by our method.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 1 , February 2023 , pp. 262 - 274
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh


