This paper investigates sharp stability estimates for the fractional Hardy–Sobolev inequality:

\begin{align*}\ \ \ \ \ \ \ \ \ \mu_{s,t}\left(\mathbb{R}^N\right) \left(\int_{\mathbb{R}^N} \frac{|u|^{2^*_s(t)}}{|x|^t} \,\mathrm{d}x \right)^{\frac{2}{2^*_s(t)}} \leq \int_{\mathbb{R}^N} \left|(-\Delta)^{\frac{s}{2}} u \right|^2 \,\mathrm{d}x, \quad \text{for all } u \in \dot{H}^s\left(\mathbb{R}^N\right)\end{align*}

where $s \in (0,1)$, 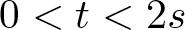$0 \lt t \lt 2s$, $N \gt 2s$ is an integer, and $2^*_s(t) = \frac{2(N-t)}{N-2s}$. Here, $\mu_{s,t}\left(\mathbb{R}^N\right)$ represents the best constant in the inequality. The primary focus is on the quantitative stability results of the above inequality and the corresponding Euler–Lagrange equation near a positive ground-state solution. Additionally, a qualitative stability result is established for the Euler–Lagrange equation, offering a thorough characterization of the Palais–Smale sequences for the associated energy functional. These results generalize the sharp quantitative stability results for the classical Sobolev inequality in $\mathbb{R}^N$, originally obtained by Bianchi and Egnell [J. Funct. Anal. 1991] as well as the corresponding critical exponent problem in $\mathbb{R}^N$, explored by Ciraolo, Figalli, and Maggi [Int. Math. Res. Not. 2017] in the framework of fractional calculus.