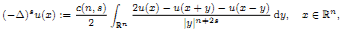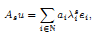Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Warma, Mahamadi
2015.
A fractional Dirichlet-to-Neumann operator on bounded Lipschitz domains.
Communications on Pure & Applied Analysis,
Vol. 14,
Issue. 5,
p.
2043.
Bonforte, Matteo
and
Vázquez, Juan Luis
2015.
A Priori Estimates for Fractional Nonlinear Degenerate Diffusion Equations on Bounded Domains.
Archive for Rational Mechanics and Analysis,
Vol. 218,
Issue. 1,
p.
317.
Carrillo, José Antonio
and
Vázquez, Juan Luis
2015.
Some free boundary problems involving non-local diffusion and aggregation.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 373,
Issue. 2050,
p.
20140275.
Grumiau, C.
Squassina, M.
and
Troestler, C.
2015.
Asymptotic symmetries for fractional operators.
Nonlinear Analysis: Real World Applications,
Vol. 26,
Issue. ,
p.
351.
Bonforte, Matteo
Sire, Yannick
and
Vázquez, Juan Luis
2015.
Existence, uniqueness and asymptotic behaviour for fractional porous medium equations on bounded domains.
Discrete and Continuous Dynamical Systems,
Vol. 35,
Issue. 12,
p.
5725.
Wang, Youtao
and
Lu, Guangcun
2015.
Generalized Solutions for Nonlocal Elliptic Equations and Systems with Nonlinear Singularities.
Abstract and Applied Analysis,
Vol. 2015,
Issue. ,
p.
1.
He, Xiaoming
Squassina, Marco
and
Zou, Wenming
2016.
The Nehari manifold for fractional systems involving critical nonlinearities.
Communications on Pure and Applied Analysis,
Vol. 15,
Issue. 4,
p.
1285.
Tzirakis, Konstantinos
2016.
Sharp trace Hardy–Sobolev inequalities and fractional Hardy–Sobolev inequalities.
Journal of Functional Analysis,
Vol. 270,
Issue. 12,
p.
4513.
Bucur, Claudia
and
Valdinoci, Enrico
2016.
Nonlocal Diffusion and Applications.
Vol. 20,
Issue. ,
p.
39.
Hu, Jianping
Wang, Xiaochao
and
Qin, Hong
2016.
Novel and efficient computation of Hilbert–Huang transform on surfaces.
Computer Aided Geometric Design,
Vol. 43,
Issue. ,
p.
95.
Vázquez, Juan Luis
2016.
The Dirichlet problem for the fractional p-Laplacian evolution equation.
Journal of Differential Equations,
Vol. 260,
Issue. 7,
p.
6038.
Bucur, Claudia
and
Valdinoci, Enrico
2016.
Nonlocal Diffusion and Applications.
Vol. 20,
Issue. ,
p.
1.
Xiang, Mingqi
Zhang, Binlin
and
Rădulescu, Vicenţiu D.
2016.
Existence of solutions for perturbed fractional p-Laplacian equations.
Journal of Differential Equations,
Vol. 260,
Issue. 2,
p.
1392.
Grubb, Gerd
2016.
Regularity of spectral fractional Dirichlet and Neumann problems.
Mathematische Nachrichten,
Vol. 289,
Issue. 7,
p.
831.
Cinti, Eleonora
Davila, Juan
and
Del Pino, Manuel
2016.
Solutions of the fractional Allen–Cahn equation which are invariant under screw motion.
Journal of the London Mathematical Society,
Vol. 94,
Issue. 1,
p.
295.
Liu, Yanmei
Khan, Monzorul
and
Yan, Yubin
2016.
Fourier Spectral Methods for Some Linear Stochastic Space-Fractional Partial Differential Equations.
Mathematics,
Vol. 4,
Issue. 3,
p.
45.
Mingqi, Xiang
Bisci, Giovanni Molica
Tian, Guohua
and
Zhang, Binlin
2016.
Infinitely many solutions for the stationary Kirchhoff problems involving the fractionalp-Laplacian.
Nonlinearity,
Vol. 29,
Issue. 2,
p.
357.
Ambrosio, Vincenzo
2016.
Infinitely Many Periodic Solutions for a Fractional Problem Under Perturbation.
Journal of Elliptic and Parabolic Equations,
Vol. 2,
Issue. 1-2,
p.
105.
Grubb, Gerd
2016.
Integration by parts and Pohozaev identities for space-dependent fractional-order operators.
Journal of Differential Equations,
Vol. 261,
Issue. 3,
p.
1835.
do Ó, João Marcos
Miyagaki, Olímpio H.
and
Squassina, Marco
2016.
Critical and subcritical fractional problems with vanishing potentials.
Communications in Contemporary Mathematics,
Vol. 18,
Issue. 06,
p.
1550063.