Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-11T08:44:41.753Z Has data issue: false hasContentIssue false
  • English
  • Français

On the essential spectrum of self-adjoint operators

Published online by Cambridge University Press:  14 November 2011

B. J. Harris
B. J. Harris
Affiliation:
University College, Cardiff
Get access Rights & Permissions [Opens in a new window]

Synopsis

We provide estimates of the form

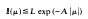
for the length of gap centre μ in the essential spectrum of a self-adjoint operator generated by a matrix differential expression.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 86 , Issue 3-4 , 1980 , pp. 261 - 274
Copyright
Copyright © Royal Society of Edinburgh 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Eastham, M. S. P.. The spectral theory of periodic differential equations (Edinburgh: Scottish Academic Press, 1973).Google Scholar
2Eastham, M. S. P.. Asymptotic estimates for the lengths of the gaps in the essential spectrum of self-adjoint differential operators. Proc. Roy. Soc. Edinburgh Sect. A 74 (1976), 239–252.Google Scholar
3Eastham, M. S. P.. Gaps in the essential spectrum of even order self-adjoint operators. Proc. London Math. Soc. 32 (1976), 213–230.Google Scholar
4Feigin, V. I.. The continuous spectrum of differential operators. Functional Anal. Appl. (1), 11 (1977), 35–44.CrossRefGoogle Scholar
5Harris, B. J.. A systematic method of estimating gaps in the essential spectrum of self-adjoint operators. J. London Math. Soc. 18 (1978), 115–132.CrossRefGoogle Scholar
6Harris, B. J.. Gaps in the essential spectra of Schrödinger and Dirac operators. J. London Math. Soc., 18 (1978), 489–502.CrossRefGoogle Scholar
7Harris, B. J.. On the spectra and stability of periodic differential equations. Proc. London Math. Soc., to appear.Google Scholar
8Lazutkin, V. F., and Pankratova, T. F.. Asymptotics of the width of gaps in the spectrum of a Sturm-Liouville operator with periodic potential. Soviet Math. Dokl. 15 (1974), 649–653.Google Scholar
9Simonyan, S. G.. Asymptotic properties of the width of gaps in the spectrum of a Sturm-Liouville operator with periodic analytic potential. Differential Equations 6 (1970), 965–71.Google Scholar
10Weidmann, J.. Oscillationmethoden für systeme gewöhnlicher Differentialgleichungen. Math. Z. 119 (1971), 349–373.CrossRefGoogle Scholar