Published online by Cambridge University Press: 09 December 2024
In this article, we study the following Schrödinger equation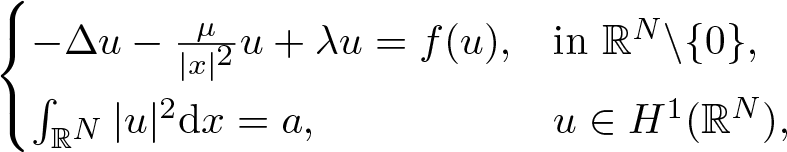 \begin{align*}\begin{cases}-\Delta u -\frac{\mu}{|x|^2} u+\lambda u =f(u), &\text{in}~ \mathbb{R}^N\backslash\{0\},\\\int_{\mathbb{R}^{N}}|u|^{2}\mathrm{d} x=a, & u\in H^1(\mathbb{R}^{N}),\end{cases}\end{align*}
\begin{align*}\begin{cases}-\Delta u -\frac{\mu}{|x|^2} u+\lambda u =f(u), &\text{in}~ \mathbb{R}^N\backslash\{0\},\\\int_{\mathbb{R}^{N}}|u|^{2}\mathrm{d} x=a, & u\in H^1(\mathbb{R}^{N}),\end{cases}\end{align*}
where 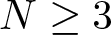 $N\geq 3$, a > 0, and
$N\geq 3$, a > 0, and 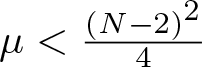 $\mu \lt \frac{(N-2)^2}{4}$. Here
$\mu \lt \frac{(N-2)^2}{4}$. Here 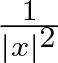 $\frac{1}{|x|^2} $ represents the Hardy potential (or ‘inverse-square potential’), λ is a Lagrange multiplier, and the nonlinearity function f satisfies the general Sobolev critical growth condition. Our main goal is to demonstrate the existence of normalized ground state solutions for this equation when
$\frac{1}{|x|^2} $ represents the Hardy potential (or ‘inverse-square potential’), λ is a Lagrange multiplier, and the nonlinearity function f satisfies the general Sobolev critical growth condition. Our main goal is to demonstrate the existence of normalized ground state solutions for this equation when 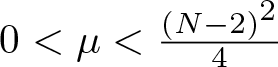 $0 \lt \mu \lt \frac{(N-2)^2}{4}$. We also analyse the behaviour of solutions as
$0 \lt \mu \lt \frac{(N-2)^2}{4}$. We also analyse the behaviour of solutions as 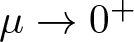 $\mu\to0^+$ and derive the existence of normalized ground state solutions for the limiting case where µ = 0. Finally, we investigate the existence of normalized solutions when µ < 0 and analyse the asymptotic behaviour of solutions as
$\mu\to0^+$ and derive the existence of normalized ground state solutions for the limiting case where µ = 0. Finally, we investigate the existence of normalized solutions when µ < 0 and analyse the asymptotic behaviour of solutions as 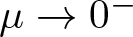 $\mu\to 0^-$.
$\mu\to 0^-$.
This work was supported by Natural Science Research Project of Guizhou Province(No. QKHJC-ZK[2023]YB033, [2023]YB036) and National Natural Science Foundation of China (No.12201147, No.12371120)