Published online by Cambridge University Press: 25 January 2019
In this paper, we analyse nonlocal equations in perforated domains. We consider nonlocal problems of the form 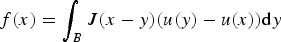 $f(x) = \int \nolimits _{B} J(x-y) (u(y) - u(x)) {\rm d}y$ with x in a perforated domain
$f(x) = \int \nolimits _{B} J(x-y) (u(y) - u(x)) {\rm d}y$ with x in a perforated domain 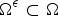 $\Omega ^\epsilon \subset \Omega $. Here J is a nonsingular kernel. We think about
$\Omega ^\epsilon \subset \Omega $. Here J is a nonsingular kernel. We think about 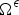 $\Omega ^\epsilon $ as a fixed set Ω from where we have removed a subset that we call the holes. We deal both with the Neumann and Dirichlet conditions in the holes and assume a Dirichlet condition outside Ω. In the latter case we impose that u vanishes in the holes but integrate in the whole ℝN (B = ℝN) and in the former we just consider integrals in ℝN minus the holes (
$\Omega ^\epsilon $ as a fixed set Ω from where we have removed a subset that we call the holes. We deal both with the Neumann and Dirichlet conditions in the holes and assume a Dirichlet condition outside Ω. In the latter case we impose that u vanishes in the holes but integrate in the whole ℝN (B = ℝN) and in the former we just consider integrals in ℝN minus the holes (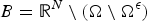 $B={\open R} ^N \setminus (\Omega \setminus \Omega ^\epsilon )$). Assuming weak convergence of the holes, specifically, under the assumption that the characteristic function of
$B={\open R} ^N \setminus (\Omega \setminus \Omega ^\epsilon )$). Assuming weak convergence of the holes, specifically, under the assumption that the characteristic function of 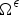 $\Omega ^\epsilon $ has a weak limit,
$\Omega ^\epsilon $ has a weak limit, 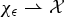 $\chi _{\epsilon } \rightharpoonup {\cal X}$ weakly* in L∞(Ω), we analyse the limit as ε → 0 of the solutions to the nonlocal problems proving that there is a nonlocal limit problem. In the case in which the holes are periodically removed balls, we obtain that the critical radius is of the order of the size of the typical cell (that gives the period). In addition, in this periodic case, we also study the behaviour of these nonlocal problems when we rescale the kernel in order to approximate local PDE problems.
$\chi _{\epsilon } \rightharpoonup {\cal X}$ weakly* in L∞(Ω), we analyse the limit as ε → 0 of the solutions to the nonlocal problems proving that there is a nonlocal limit problem. In the case in which the holes are periodically removed balls, we obtain that the critical radius is of the order of the size of the typical cell (that gives the period). In addition, in this periodic case, we also study the behaviour of these nonlocal problems when we rescale the kernel in order to approximate local PDE problems.