Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-25T12:42:09.293Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonchaotic N-expansive homeomorphisms

Part of: Topological dynamics Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  31 August 2023

Woochul Jung  and
C. A. Morales
Woochul Jung
Affiliation:
Healthcare Data Science Center, Konyang University Hospital, Daejeon, Republic of Korea (wcjungdynamics@gmail.com)
C. A. Morales
Affiliation:
Instituto de Matemática, Universidade Federal do Rio de Janeiro, P. O. Box 68530, 21945-970 Rio de Janeiro, Brazil (morales@impa.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we give necessary conditions for an $N$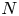-expansive homeomorphism of a compact metric space to be nonchaotic in the Li–Yorke sense. As application we give a partial answer to a conjecture in [2].

Keywords

compact metric spaceexpansiveN-expansive

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Secondary: 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 9
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blanchard, F., Glasner, E., Kolyada, S. and Maass, A.. On Li-Yorke pairs. J. Reine Angew. Math. 547 (2002), 51–68.Google Scholar
Carvalho, B. and Cordeiro, W.. $N$-expansive homeomorphisms with the shadowing property. J. Differ. Equ. 261 (2016), 3734–3755.CrossRefGoogle Scholar
Dong, M., Lee, K. and Shin, B.. Characterization of $N$-expansive systems. Preprint (2023) (To appear).Google Scholar
Kato, H.. Chaotic continua of (continuum-wise) expansive homeomorphisms and chaos in the sense of Li and Yorke. Fundam. Math. 145 (1994), 261–279.CrossRefGoogle Scholar
Lee, K., Morales, C. A. and Villavicencio, H.. Asymptotic expansivity. J. Math. Anal. Appl. 507 (2022), 125729.CrossRefGoogle Scholar
Li, T. Y. and Yorke, J. A.. Period three implies chaos. Am. Math. Mon. 82 (1975), 985–992.CrossRefGoogle Scholar
Li, J. and Zhang, R.. Levels of generalized expansiveness. J. Dyn. Differ. Equ. 29 (2017), 877–894.CrossRefGoogle Scholar
Morales, C. A.. A generalization of expansivity. Discrete Contin. Dyn. Syst. 32 (2012), 293–301.CrossRefGoogle Scholar
Sears, M.. Expansiveness of locally compact spaces. Math. Syst. Theory 7 (1974), 377–382.CrossRefGoogle Scholar
Utz, W. R.. Unstable homeomorphisms. Proc. Am. Math. Soc. 1 (1950), 769–774.CrossRefGoogle Scholar
Walters, P.. On the pseudo-orbit tracing property and its relationship to stability. The structure of attractors in dynamical systems. Proc. Conf., North Dakota State Univ., Fargo, N.D., 1977. Lecture Notes in Math., vol. 668, pp. 231–244 (1978).CrossRefGoogle Scholar