No CrossRef data available.
Article contents
Multi-clustered solutions for a singularly perturbed forced pendulum equation
Published online by Cambridge University Press: 26 January 2019
Abstract
In this paper, we are concerned with unbounded solutions of the singularly perturbed forced pendulum equation in the presence of friction, namely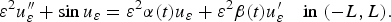 $$\varepsilon ^2u_\varepsilon ^{{\prime}{\prime}} + \sin u_\varepsilon = \varepsilon ^2\alpha (t)u_\varepsilon + \varepsilon ^2\beta (t)u_\varepsilon ^{\prime} \quad {\rm in}\;(-L,L).{\rm }$$
$$\varepsilon ^2u_\varepsilon ^{{\prime}{\prime}} + \sin u_\varepsilon = \varepsilon ^2\alpha (t)u_\varepsilon + \varepsilon ^2\beta (t)u_\varepsilon ^{\prime} \quad {\rm in}\;(-L,L).{\rm }$$
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 1 , February 2020 , pp. 387 - 417
- Copyright
- Copyright © Royal Society of Edinburgh 2019

