No CrossRef data available.
A link between the shape of the austenite–martensite interface and the behaviour of the surface energy
Published online by Cambridge University Press: 12 July 2007
Abstract
Let Ω ⊂ R2 denote a bounded Lipschitz domain and consider some portion Γ0 of ∂Ω representing the austenite–twinned-martensite interface which is not assumed to be a straight segment. We prove that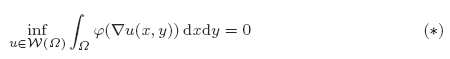 for an elastic energy density ϖ: R2 → [0 ∞) such that ϖ(0, ±1) = 0. Here, W(Ω) consists of all functions u from the Sobolev class W1, ∞(Ω) such that |uy| = 1 almost everywhere on Ω together with u = 0 on Γ0. We will first show that, for Γ0 having a vertical tangent, one cannot always expect a finite surface energy, i.e. in the above problem, the condition
for an elastic energy density ϖ: R2 → [0 ∞) such that ϖ(0, ±1) = 0. Here, W(Ω) consists of all functions u from the Sobolev class W1, ∞(Ω) such that |uy| = 1 almost everywhere on Ω together with u = 0 on Γ0. We will first show that, for Γ0 having a vertical tangent, one cannot always expect a finite surface energy, i.e. in the above problem, the condition  in general cannot be included. This generalizes a result of [12] where Γ0is a vertical straight line. Property (*) is established by constructing some minimizing sequences vanishing on the whole boundary ∂Ω, that is, one can even take Γ0 = ∂Ω. We also show that the existence or non-existence of minimizers depends on the shape of the austenite–twinned-martensite interface Γ0.
in general cannot be included. This generalizes a result of [12] where Γ0is a vertical straight line. Property (*) is established by constructing some minimizing sequences vanishing on the whole boundary ∂Ω, that is, one can even take Γ0 = ∂Ω. We also show that the existence or non-existence of minimizers depends on the shape of the austenite–twinned-martensite interface Γ0.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 134 , Issue 6 , December 2004 , pp. 1099 - 1113
- Copyright
- Copyright © Royal Society of Edinburgh 2004

