Hostname: page-component-6bb9c88b65-vmslq Total loading time: 0 Render date: 2025-07-23T18:59:37.928Z Has data issue: false hasContentIssue false
  • English
  • Français

Ground state solution for weakly coupled time-harmonic Maxwell’s equations with critical exponent

Part of: Equations of mathematical physics and other areas of application Elliptic equations and systems Partial differential equations Optics, electromagnetic theory - General

Published online by Cambridge University Press:  18 July 2025

Zhen Song
Zhen Song*
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing, China (sz21@mails.tsinghua.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we deal with the following nonlinear time-harmonic Maxwell’s equations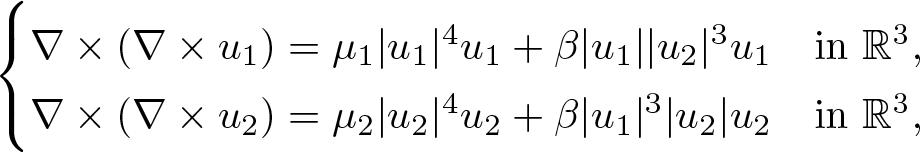

\begin{equation*}\nonumber\begin{cases} \nabla \times(\nabla \times u_1)=\mu_1|u_1|^4u_1+\beta|u_1||u_2|^3u_1 & \text {in } \mathbb{R}^3, \\ \nabla \times(\nabla \times u_2)=\mu_2|u_2|^4u_2+\beta|u_1|^3|u_2|u_2 & \text {in } \mathbb{R}^3, \end{cases}\end{equation*}
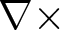where $\nabla\times$ denotes the usual curl operator in 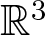$\mathbb{R}^3$, 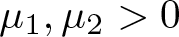$\mu_1,\mu_2 \gt 0$, and 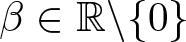$\beta\in\mathbb{R}\backslash\{0\}$. We show that this critical system admits a non-trivial ground state solution when the parameter β is positive and small. For general 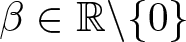$\beta\in\mathbb{R}\backslash\{0\}$, we prove that this system admits a non-trivial cylindrically symmetric solution with the least positive energy. We also study the existence of the curl-free solution and the synchronized solution due to the special structure of this system. These seem to be the first results on the critically coupled system containing the curl-curl operator.

Keywords

critically coupled systemcylindrically symmetric solutionground state solutionnonlinear time-harmonic Maxwell’s equations

MSC classification

Primary: 35Q60: PDEs in connection with optics and electromagnetic theory
Secondary: 35J20: Variational methods for second-order elliptic equations 35B33: Critical exponents 78A25: Electromagnetic theory, general

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 31
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Amrouche, C., Bernardi, C., Dauge, M. and Girault, V.. Vector potentials in three-dimensional non-smooth domains. Math. Methods Appl. Sci. 21 (1998), 823–864.10.1002/(SICI)1099-1476(199806)21:9<823::AID-MMA976>3.0.CO;2-B3.0.CO;2-B>CrossRefGoogle Scholar
Azzollini, A., Benci, V., D’Aprile, T. and Fortunato, D.. Existence of static solutions of the semilinear Maxwell equations. Ric. Mat. 55 (2006), 283–297.10.1007/s11587-006-0016-8CrossRefGoogle Scholar
Bartsch, T. and Ding, Y.. Deformation theorems on non-metrizable vector spaces and applications to critical point theory. Math. Nachr. 279 (2006), 1267–1288.10.1002/mana.200410420CrossRefGoogle Scholar
Bartsch, T., Dohnal, T., Plum, M. and Reichel, W.. Ground states of a nonlinear curl-curl problem in cylindrically symmetric media. NoDEA Nonlinear Differential Equations Appl. 23 (2016), .10.1007/s00030-016-0403-0CrossRefGoogle Scholar
Bartsch, T. and Mederski, J.. Ground and bound state solutions of semilinear time-harmonic Maxwell equations in a bounded domain. Arch. Rational Mech. Anal. 215 (2015), 283–306.10.1007/s00205-014-0778-1CrossRefGoogle Scholar
Bartsch, T. and Mederski, J.. Nonlinear time-harmonic Maxwell equations in domains. J. Fixed Point Theory Appl. 19 (2017), 959–986.10.1007/s11784-017-0409-1CrossRefGoogle Scholar
Benci, V. and Fortunato, D.. Towards a unified field theory for classical electrodynamics. Arch. Ration. Mech. Anal. 173 (2004), 379–414.10.1007/s00205-004-0324-7CrossRefGoogle Scholar
Bieganowski, B.. Solutions to a nonlinear Maxwell equation with two competing nonlinearities in $\mathbb{R}^3$. Bull. Pol. Acad. Sci. Math. 69 (2021), 37–60.10.4064/ba210731-19-8CrossRefGoogle Scholar
Borwein, J., Guirao, A. J., Hájek, P. and Vanderwerff, J.. Uniformly convex functions on Banach spaces. Proc. Amer. Math. Soc. 137 (2009), 1081–1091.10.1090/S0002-9939-08-09630-5CrossRefGoogle Scholar
Brézis, H. and Lie, E.. A relation between pointwise convergence of functions and convergence of functionals. Proc. Amer. Math. Soc. 88 (1983), 486–490.10.1090/S0002-9939-1983-0699419-3CrossRefGoogle Scholar
Chen, Z., Du, Q. and Zou, J.. Finite element methods with matching and nonmatching meshes for Maxwell equations with discontinuous coefficients. SIAM J. Numer. Anal. 37 (2000), 1542–1570.10.1137/S0036142998349977CrossRefGoogle Scholar
Chen, Z. and Zou, W.. Existence and symmetry of positive ground states for a doubly critical Schrödinger system. Trans. Amer. Math. Soc. 367 (2015), 3599–3646.10.1090/S0002-9947-2014-06237-5CrossRefGoogle Scholar
Chen, Z. and Zou, W.. Positive least energy solutions and phase separation for coupled Schrödinger equations with critical exponent: higher dimensional case. Calc. Var. Partial Differential Equations. 52 (2015), 423–467.10.1007/s00526-014-0717-xCrossRefGoogle Scholar
Clapp, M. and Pistoia, A.. Existence and phase separation of entire solutions to a pure critical competitive elliptic system. Calc. Var. Partial Differential Equations. 57 (2018), .10.1007/s00526-017-1283-9CrossRefGoogle Scholar
Ding, W.. On a conformally invariant elliptic equation on $ \lt b \gt R \lt /b \gt ^n$. Comm. Math. Phys. 107 (1986), 331–335.Google Scholar
Evans, L. C.. Weak convergence methods for nonlinear partial differential equations, CBMS Regional Conference Series in Mathematics # 74. AMS, Providence, RI (1990), 12–14.10.1090/cbms/074CrossRefGoogle Scholar
Gaczkowski, M., Mederski, J. and Schino, J.. Multiple solutions to cylindrically symmetric curl-curl problems and related Schrödinger equations with singular potentials. SIAM J. Math. Anal. 55 (2023), 4425–4444.10.1137/22M1494786CrossRefGoogle Scholar
Hirsch, A. and Reichel, W.. Existence of cylindrically symmetric ground states to a nonlinear curl-curl equation with non-constant coefficients. Z. Anal. Anwend. 36 (2017), 419–435.10.4171/zaa/1595CrossRefGoogle Scholar
Kirsch, A. and Hettlich, F.. The Mathematical Theory of Time-Harmonic Maxwell’s Equations: Expansion, Integral, and Variational Methods. Springer, Berlin. (2015).Google Scholar
Leinfelder, H.. Gauge invariance of Schrödinger operators and related spectral properties. J. Oper. Theory. 9 (1983), 163–179.Google Scholar
Mandel, R.. Uncountably many solutions for nonlinear Helmholtz and curl-curl equations. Adv. Nonlinear Stud. 19 (2019), 569–593.10.1515/ans-2019-2050CrossRefGoogle Scholar
Mederski, J.. Ground states of time-harmonic semilinear Maxwell equations in $\mathbb{R}^3$ with vanishing permittivity. Arch. Rational Mech. Anal. 218 (2015), 825–861.10.1007/s00205-015-0870-1CrossRefGoogle Scholar
Mederski, J.. The Brezis-Nirenberg problem for the curl-curl operator. J. Funct. Anal. 274 (2018), 1345–1380.10.1016/j.jfa.2017.12.012CrossRefGoogle Scholar
Mederski, J.. Nonlinear time-harmonic Maxwell equations in a bounded domain: lack of compactness. Sci. China Math. 61 (2018), 1963–1970.10.1007/s11425-017-9312-8CrossRefGoogle Scholar
Mederski, J. and Schino, J.. Nonlinear curl-curl problems in $\mathbb{R}^3$. Minimax Theory Appl. 7 (2022), 339–364.Google Scholar
Mederski, J., Schino, J. and Szulkin, A.. Multiple solutions to a nonlinear curl–curl problem in ${\mathbb{R}}^3$. Arch. Ration. Mech. Anal. 236 (2020), 253–288.10.1007/s00205-019-01469-3CrossRefGoogle Scholar
Mederski, J. and Szulkin, A.. A Sobolev-type inequality for the curl operator and ground states for the curl-curl equation with critical Sobolev exponent. Arch. Ration. Mech. Anal. 241 (2021), 1815–1842.10.1007/s00205-021-01684-xCrossRefGoogle Scholar
Monk, P.. Finite Element Methods for Maxwell’s Equations. (Oxford University Press, New York, 2003).10.1093/acprof:oso/9780198508885.001.0001CrossRefGoogle Scholar
Palais, R. S.. The principle of symmetric criticality. Comm. Math. Phys. 69 (1979), 19–30.10.1007/BF01941322CrossRefGoogle Scholar
Picard, R., Weck, N. and Witsch, K. -J.. Time-harmonic Maxwell equations in the exterior of perfectly conducting, irregular obstacles. Analysis (Munich). 21 (2001), 231–263.Google Scholar
Saleh, B. E. A. and Teich, M. C.. Fundamentals of Photonics. Wiley, New York. (2007), 2nd edition.Google Scholar
Song, Z., Sun, J. and Zou, W.. The Lane-Emden system for curl-curl operator. preprint. (2024).Google Scholar
Struwe, M.. Variational Methods, Fourth Edition [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Vol.34, (Springer-Verlag, Berlin., 2008).Google Scholar
Stuart, C. A.. Self-trapping of an electromagnetic field and bifurcation from the essential spectrum. Arch. Rational Mech. Anal. 113 (1990), 65–96.10.1007/BF00380816CrossRefGoogle Scholar
Stuart, C. A.. Guidance properties of nonlinear planar waveguides. Arch. Rational Mech. Anal. 125 (1993), 145–200.10.1007/BF00376812CrossRefGoogle Scholar
Stuart, C. A. and Zhou, H. -S.. Axisymmetric TE-modes in a self-focusing dielectric. SIAM J. Math. Anal. 37 (2005), 218–237.10.1137/S0036141004441751CrossRefGoogle Scholar
Stuart, C. A. and Zhou, H. -S.. Existence of guided cylindrical TM-modes in an inhomogeneous self-focusing dielectric. Math. Models Methods Appl. Sci. 20 (2010), 1681–1719.10.1142/S0218202510004751CrossRefGoogle Scholar
Szulkin, A. and Weth, T.. Ground state solutions for some indefinite variational problems. J. Funct. Anal. 257 (2009), 3802–3822.10.1016/j.jfa.2009.09.013CrossRefGoogle Scholar
Waliullah, S.. Minimizers and symmetric minimizers for problems with critical Sobolev exponent. Topol. Methods Nonlinear Anal. 34 (2009), 291–326.10.12775/TMNA.2009.044CrossRefGoogle Scholar
Wen, Y. and Zhao, P.. Infinitely many cylindrically symmetric solutions of nonlinear Maxwell equations with concave and convex nonlinearities. Z. Angew. Math. Phys. 73 (2022), .10.1007/s00033-022-01868-9CrossRefGoogle Scholar
Wen, Y. and Zhao, P.. Ground state solution of weakly coupled time-harmonic Maxwell equations. Z. Angew. Math. Phys. 74 (2023), .10.1007/s00033-023-01987-xCrossRefGoogle Scholar
Willem, M.. Minimax Theorems. (Birkhäuser Boston, Inc., Boston, MA, 1996).10.1007/978-1-4612-4146-1CrossRefGoogle Scholar
Ye, H. and Peng, Y.. Positive least energy solutions for a coupled Schrödinger system with critical exponent. J. Math. Anal. Appl. 417 (2014), 308–326.10.1016/j.jmaa.2014.03.028CrossRefGoogle Scholar
Zeng, X.. Cylindrically symmetric ground state solutions for curl-curl equations with critical exponent. Z. Angew. Math. Phys. 68 (2017), .10.1007/s00033-017-0887-4CrossRefGoogle Scholar