No CrossRef data available.
Article contents
Fourier coefficients of functions in power-weighted L2-spaces and conditionality constants of bases in Banach spaces
Published online by Cambridge University Press: 30 March 2022
Abstract
We prove that, given $2< p<\infty$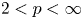 , the Fourier coefficients of functions in $L_2(\mathbb {T}, |t|^{1-2/p}\,{\rm d}t)$
, the Fourier coefficients of functions in $L_2(\mathbb {T}, |t|^{1-2/p}\,{\rm d}t)$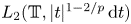 belong to $\ell _p$
belong to $\ell _p$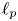 , and that, given $1< p<2$
, and that, given $1< p<2$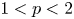 , the Fourier series of sequences in $\ell _p$
, the Fourier series of sequences in $\ell _p$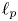 belong to $L_2(\mathbb {T}, \vert {t}\vert ^{2/p-1}\,{\rm d}t)$
belong to $L_2(\mathbb {T}, \vert {t}\vert ^{2/p-1}\,{\rm d}t)$ . Then, we apply these results to the study of conditional Schauder bases and conditional almost greedy bases in Banach spaces. Specifically, we prove that, for every $1< p<\infty$
. Then, we apply these results to the study of conditional Schauder bases and conditional almost greedy bases in Banach spaces. Specifically, we prove that, for every $1< p<\infty$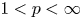 and every $0\le \alpha <1$
and every $0\le \alpha <1$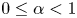 , there is a Schauder basis of $\ell _p$
, there is a Schauder basis of $\ell _p$ whose conditionality constants grow as $(m^{\alpha })_{m=1}^{\infty }$
whose conditionality constants grow as $(m^{\alpha })_{m=1}^{\infty }$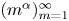 , and there is an almost greedy basis of $\ell _p$
, and there is an almost greedy basis of $\ell _p$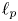 whose conditionality constants grow as $((\log m)^{\alpha })_{m=2}^{\infty }$
whose conditionality constants grow as $((\log m)^{\alpha })_{m=2}^{\infty }$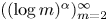 .
.
Keywords
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 3 , June 2023 , pp. 784 - 810
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh


