Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-11T13:01:04.428Z Has data issue: false hasContentIssue false
  • English
  • Français

Fatou components and singularities of meromorphic functions

Part of: Complex dynamical systems Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  23 January 2019

Krzysztof Barański ,
Núria Fagella ,
Xavier Jarque  and
Bogusława Karpińska
Krzysztof Barański
Affiliation:
Institute of Mathematics, University of Warsaw, ul. Banacha 2, 02-097Warszawa, Poland (baranski@mimuw.edu.pl)
Núria Fagella
Affiliation:
Departament de Matemàtiques i Informàtica, Institut de Matemàtiques de la Universitat de Barcelona (IMUB) and Barcelona Graduate School of Mathematics (BGSMath). Gran Via 585, 08007Barcelona, Catalonia, Spain (nfagella@ub.edu; xavier.jarque@ub.edu)
Xavier Jarque
Affiliation:
Departament de Matemàtiques i Informàtica, Institut de Matemàtiques de la Universitat de Barcelona (IMUB) and Barcelona Graduate School of Mathematics (BGSMath). Gran Via 585, 08007Barcelona, Catalonia, Spain (nfagella@ub.edu; xavier.jarque@ub.edu)
Bogusława Karpińska
Affiliation:
Faculty of Mathematics and Information Science, Warsaw University of Technology, ul. Koszykowa 75, 00-662Warszawa, Poland (bkarpin@mini.pw.edu.pl)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove several results concerning the relative position of points in the postsingular set P(f) of a meromorphic map f and the boundary of a Baker domain or the successive iterates of a wandering component. For Baker domains we answer a question of Mihaljević-Brandt and Rempe-Gillen. 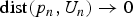For wandering domains we show that if the iterates Un of such a domain have uniformly bounded diameter, then there exists a sequence of postsingular values pn such that ${\rm dist} (p_n, U_n)\to 0$ as 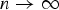$n\to \infty $. We also prove that if 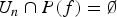$U_n \cap P(f)=\emptyset $ and the postsingular set of f lies at a positive distance from the Julia set (in ℂ), then the sequence of iterates of any wandering domain must contain arbitrarily large disks. This allows to exclude the existence of wandering domains for some meromorphic maps with infinitely many poles and unbounded set of singular values.

Keywords

transcendental dynamicsJulia setBaker domainwandering domain

MSC classification

Primary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Secondary: 37F10: Polynomials; rational maps; entire and meromorphic functions 30D30: Meromorphic functions, general theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 633 - 654
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Baker, I. N.. An entire function which has wandering domains. J. Austral. Math. Soc. Ser. A 22 (1976), 173–176. MR 0419759.CrossRefGoogle Scholar
2Baker, I. N.. Wandering domains in the iteration of entire functions. Proc. London Math. Soc. (3) 49 (1984), 563–576. MR 759304.CrossRefGoogle Scholar
3Baker, I. N.. Limit functions in wandering domains of meromorphic functions. Ann. Acad. Sci. Fenn. Math. 27 (2002), 499–505. MR 1922204.Google Scholar
4Baker, I. N., Kotus, J. and Yinian, L.. Iterates of meromorphic functions. II. Examples of wandering domains. J. London Math. Soc. (2) 42 (1990), 267–278. MR 1083445.CrossRefGoogle Scholar
5Baker, I. N., Kotus, J. and Yinian, L.. Iterates of meromorphic functions. I. Ergodic Theory Dynam. Systems 11 (1991), 241–248. MR 1116639 (92m:58113).CrossRefGoogle Scholar
6Baker, I. N., Kotus, J. and Yinian, L.. Iterates of meromorphic functions. III. Preperiodic domains. Ergodic Theory Dynam. Systems 11 (1991), 603–618. MR 1145612 (92m:58115).CrossRefGoogle Scholar
7Baker, I. N., Kotus, J. and Yinian, L.. Iterates of meromorphic functions. IV. Critically finite functions. Results Math. 22 (1992), 651–656. MR 1189754.CrossRefGoogle Scholar
8Barański, K. and Fagella, N.. Univalent Baker domains. Nonlinearity 14 (2001), 411–429. MR 1830901 (2002d:37069).CrossRefGoogle Scholar
9Barański, K., Fagella, N., Jarque, X. and Karpińska, B.. On the connectivity of the Julia sets of meromorphic functions. Invent. Math. 198 (2014), 591–636. MR 3279533.CrossRefGoogle Scholar
10Barański, K., Fagella, N., Jarque, X. and Karpińska, B.. Absorbing sets and Baker domains for holomorphic maps. J. Lond. Math. Soc. (2) 92 (2015), 144–162. MR 3384509.CrossRefGoogle Scholar
11Barański, K., Fagella, N., Jarque, X. and Karpińska, B.. Accesses to infinity from Fatou components. Trans. Amer. Math. Soc. 369 (2017), 1835–1867. MR 3581221.CrossRefGoogle Scholar
12Barański, K., Fagella, N., Jarque, X. and Karpińska, B.. On the connectivity of the Julia set of Newton maps: a unified approach. Rev. Mat. Iberoam. 34 (2018), 1211–1228.CrossRefGoogle Scholar
13Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. (N.S.) 29 (1993), 151–188. MR 1216719 (94c:30033).CrossRefGoogle Scholar
14Bergweiler, W.. Newton's method and a class of meromorphic functions without wandering domains. Ergodic Theory Dynam. Systems 13 (1993), 231–247. MR 1235471.CrossRefGoogle Scholar
15Bergweiler, W.. Invariant domains and singularities. Math. Proc. Cambridge Philos. Soc. 117 (1995), 525–532. MR 1317494.CrossRefGoogle Scholar
16Bergweiler, W. and Terglane, N.. Weakly repelling fixpoints and the connectivity of wandering domains. Trans. Amer. Math. Soc. 348 (1996), 1–12. MR 1327252 (96e:30055).CrossRefGoogle Scholar
17Bergweiler, W., Haruta, M., Kriete, H., Meier, H.-G. and Terglane, N.. On the limit functions of iterates in wandering domains. Ann. Acad. Sci. Fenn. Ser. A I Math. 18 (1993), 369–375. MR 1234740.Google Scholar
18Bergweiler, W., Rippon, P. J. and Stallard, G. M.. Multiply connected wandering domains of entire functions. Proc. Lond. Math. Soc. (3) 107 (2013), 1261–1301. MR 3149847.CrossRefGoogle Scholar
19Carleson, L. and Gamelin, T. W.. Complex dynamics, Universitext: Tracts in Mathematics (New York: Springer-Verlag, 1993). MR 1230383 (94h:30033).CrossRefGoogle Scholar
20Erëmenko, A. È. and Lyubich, M. Y.. Examples of entire functions with pathological dynamics. J. London Math. Soc. (2) 36 (1987), 458–468. MR 918638.CrossRefGoogle Scholar
21Erëmenko, A. È. and Lyubich, M. Y.. Dynamical properties of some classes of entire functions. Ann. Inst. Fourier (Grenoble) 42 (1992), 989–1020. MR 1196102 (93k:30034).CrossRefGoogle Scholar
22Fagella, N. and Henriksen, C.. Deformation of entire functions with Baker domains. Discrete Contin. Dyn. Syst. 15 (2006), 379–394. MR 2199435 (2006i:37106).CrossRefGoogle Scholar
23Fagella, N. and Henriksen, C.. The Teichmüller space of an entire function, Complex dynamics, pp. 297–330 (Wellesley, MA: A K Peters, 2009). MR 2508262 (2011c:37101).Google Scholar
24Goldberg, L. R. and Keen, L.. A finiteness theorem for a dynamical class of entire functions. Ergodic Theory Dynam. Systems 6 (1986), 183–192. MR 857196 (88b:58126).CrossRefGoogle Scholar
25Kisaka, M. and Shishikura, M.. On multiply connected wandering domains of entire functions, Transcendental dynamics and complex analysis, London Math. Soc. Lecture Note Ser., vol. 348, pp. 217–250 (Cambridge: Cambridge Univ. Press, 2008). MR 2458806.Google Scholar
26Kotus, J. and Urbański, M.. The dynamics and geometry of the Fatou functions. Discrete Contin. Dyn. Syst. 13 (2005), 291–338. MR 2152392.CrossRefGoogle Scholar
27Kriete, H.. On the Newton's method for transcendental functions. J. Math. Kyoto Univ. 41 (2001), 611–625. MR 1878723.CrossRefGoogle Scholar
28Mayer, V. and Urbański, M.. Fractal measures for meromorphic functions of finite order. Dyn. Syst. 22 (2007), 169–178. MR 2327991.CrossRefGoogle Scholar
29Mayer, V. and Urbański, M.. Thermodynamical formalism and multifractal analysis for meromorphic functions of finite order. Mem. Amer. Math. Soc. 203 (2010), vi+107. MR 2590263.Google Scholar
30Mihaljević-Brandt, H. and Rempe-Gillen, L.. Absence of wandering domains for some real entire functions with bounded singular sets. Math. Ann. 357 (2013), 1577–1604. MR 3124942.CrossRefGoogle Scholar
31Rippon, P. J.. Baker domains of meromorphic functions. Ergodic Theory Dynam. Systems 26 (2006), 1225–1233. MR 2247639 (2008d:37074).CrossRefGoogle Scholar
32Rippon, P. J.. Baker domains, Transcendental dynamics and complex analysis, London Math. Soc. Lecture Note Ser., vol. 348, pp. 371–395 (Cambridge: Cambridge Univ. Press, 2008). MR 2458809 (2009j:30061).Google Scholar
33Rippon, P. J. and Stallard, G. M.. Iteration of a class of hyperbolic meromorphic functions. Proc. Amer. Math. Soc. 127 (1999), 3251–3258. MR 1610785.CrossRefGoogle Scholar
34Stallard, G. M.. Entire functions with Julia sets of zero measure. Math. Proc. Cambridge Philos. Soc. 108 (1990), 551–557. MR 1068456.CrossRefGoogle Scholar
35Stallard, G. M.. A class of meromorphic functions with no wandering domains. Ann. Acad. Sci. Fenn. Ser. A I Math. 16 (1991), 211–226. MR 1139794.CrossRefGoogle Scholar
36Sullivan, D.. Quasiconformal homeomorphisms and dynamics. I. Solution of the Fatou-Julia problem on wandering domains. Ann. of Math. (2) 122 (1985), 401–418. MR 819553 (87i:58103).CrossRefGoogle Scholar
37Zheng, J.-H.. Singularities and limit functions in iteration of meromorphic functions. J. London Math. Soc. (2) 67 (2003), 195–207. MR 1942420.CrossRefGoogle Scholar