No CrossRef data available.
Article contents
Double EPW sextics associated with Gushel–Mukai surfaces
Published online by Cambridge University Press: 23 December 2024
Abstract
Works by O’Grady allow to associate with a two-dimensional Gushel–Mukai (GM) variety, which is a K3 surface, a double Eisenbud–Popescu–Walter (EPW) sextic. We characterize the 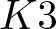 $K3$ surfaces whose associated double EPW sextic is smooth. As a consequence, we are able to produce symplectic actions on some families of smooth double EPW sextics which are hyper-Kähler manifolds.
$K3$ surfaces whose associated double EPW sextic is smooth. As a consequence, we are able to produce symplectic actions on some families of smooth double EPW sextics which are hyper-Kähler manifolds.
We also provide bounds for the automorphism group of GM varieties in dimension 2 and higher.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Garbagnati, A. and Sarti, A.. Elliptic fibrations and symplectic automorphisms on K3 surfaces. Comm. Alg. 37 (2009), 3601–3631.CrossRefGoogle Scholar
Garbagnati, A.. Elliptic K3 surfaces with abelian and dihedral groups of symplectic automorphisms. Comm. Alg. 41 (2013), 583–616.CrossRefGoogle Scholar
Ferretti, A.. The Chow ring of double EPW sextics. Alg. Num. Theo. 6 (2012), 539–560.CrossRefGoogle Scholar
Iliev, A. and Manivel, L.. Fano manifolds of degree ten and EPW sextics. Annales Scientifiques de l’ÉCole Normale Supérieure 44 (2011), 393–426.CrossRefGoogle Scholar
Huybrechts, D.. Lectures on K3 surfaces, Vol. 158 (Cambridge University Press, 2016).CrossRefGoogle Scholar
Eisenbud, D., Popescu, S. and Walter, C.. Lagrangian subbundles and codimension 3 subcanonical subschemes. Duke Math. J. 107 (2001), 427–467.CrossRefGoogle Scholar
Greer, FG., Li, Z. and Tian, Z.. Picard groups on moduli of K3 surfaces with Mukai models. Int. Math. Res. Not. 16 (2015), 7238–7257.CrossRefGoogle Scholar
Xiao, G.. Galois covers between  $K3$ surfaces. Annales de l’Institut fourier 46 (1996), 73–88.CrossRefGoogle Scholar
$K3$ surfaces. Annales de l’Institut fourier 46 (1996), 73–88.CrossRefGoogle Scholar
Mongardi, G.. On symplectic automorphisms of hyper-Kähler fourfolds of K3 [2] type. Michigan Math. J. 62 (2013), 537–550.CrossRefGoogle Scholar
Mongardi, G.. Towards a classification of symplectic automorphisms on manifolds of K3 [n]-type. Math. Z. 282 (2016), 651–662.CrossRefGoogle Scholar
Iskovskikh, V. A. and Prokhorov, Y. G.. Algebraic geometry V. Fano varieties, Encyclopaedia of Mathematical Sciences, 47, 1–247. (Berlin: Springer, 1999).Google Scholar
Piontkowski, J. and Van de Ven, A.. The automorphism group of linear sections of the Grassmannians G (1, N). Doc. Math. 4 (1999), 623–664.CrossRefGoogle Scholar
O’Grady, K. G.. Involutions and linear systems on holomorphic symplectic manifolds. Geo. Funct. Anal. GAFA 15 (2005), 1223–1274.CrossRefGoogle Scholar
O’Grady, K. G.. Irreducible symplectic 4-folds and Eisenbud-Popescu-Walter sextics. Duke Math. J. 134 (2006), 99–137.Google Scholar
O’Grady, K. G.. Dual double EPW-sextics and their periods. Pure Appl. Math. Quart. 4 (2008), 427–468.CrossRefGoogle Scholar
Mecchia, M. and Zimmermann, B.. On finite groups acting on homology 4-spheres and finite subgroups of SO (5). Top. Appl. 158 (2011), 741–747.CrossRefGoogle Scholar
Debarre, O. and Kuznetsov, A.. Gushel–Mukai varieties: Classification and birationalities. Alg. Geo. 5 (2018), 15–76.Google Scholar
Debarre, O. and Kuznetsov, A.. Double covers of quadratic degeneracy and Lagrangian intersection loci. Math. Ann. 378 (2019), 1435–1469.CrossRefGoogle Scholar
Debarre, O. and Kuznetsov, A.. Gushel–Mukai varieties: Linear spaces and periods. Kyoto J. Math. 59 (2019), 857–953.CrossRefGoogle Scholar
Debarre, O. and Kuznetsov, A.. Gushel–Mukai varieties: Intermediate Jacobians. Épijournal Géom. Algébrique 4 (2020).Google Scholar
Debarre, O. and Kuznetsov, A.. Gushel–Mukai varieties: Moduli. Int. J. Math. 31 (2020), .CrossRefGoogle Scholar
Debarre, O., Iliev, A. and Manivel, L.. Special prime Fano fourfolds of degree 10 and index 2. Rec. Adv. Alg. Geo. 417 (2014), .Google Scholar
Debarre, O. and Macrì, E.. On the period map for polarized hyperkähler fourfolds. Int. Math. Res. Not. 2019 (2019), 6887–6923.CrossRefGoogle Scholar
Debarre, O. and Mongardi, G.. Gushel–Mukai varieties with many symmetries and an explicit irrational Gushel–Mukai threefold. Bollettino dell’Unione Matematica Italiana 15 (2022), 133–161.CrossRefGoogle Scholar
Mukai, S.. New developments in the theory of Fano threefolds: Vector bundle method and moduli problems. Sugaku 47 (1995), 124–144.Google Scholar
Nikulin, V. V.. Finite groups of automorphisms of Kählerian K 3 surfaces. Trudy Moskovskogo Matematicheskogo Obshchestva 38 (1979), 75–137.Google Scholar
Nikulin, V.V.. Integral symmetric bilinear forms and some of their applications. Izvestiya Rossiiskoi Akademii Nauk. Seriya Matematicheskaya 43 (1979), 111–177.Google Scholar
Gritsenko, V. A., Hulek, K. and Sankaran, G. K.. Abelianisation of orthogonal groups and the fundamental group of modular varieties. J. Alg. 322 (2009), 463–478.CrossRefGoogle Scholar
Gritsenko, V. A., Hulek, K. and Sankaran, G. K.. Moduli spaces of irreducible symplectic manifolds. Comp. Math. 146 (2010), 404–434.CrossRefGoogle Scholar
Gritsenko, V. A., Hulek, K. and Sankaran, G. K.. Moduli of K3 surfaces and irreducible symplectic manifolds. Handbook of Moduli. Vol. I, Adv. Lect. Math. 24 (2013), 459–526.Google Scholar


