Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chapman, S. J.
King, J. R.
and
Adams, K. L.
1998.
Exponential asymptotics and Stokes lines in nonlinear ordinary differential equations.
Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 454,
Issue. 1978,
p.
2733.

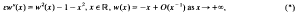
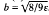 In particular there are no even solutions of problem (*) for any ε > 0.
In particular there are no even solutions of problem (*) for any ε > 0.