Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kreith, Kurt
1981.
A class of comparison theorems for non-linear hyperbolic initial value problems.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 87,
Issue. 3-4,
p.
189.
Hsiang, Wu-Teh
and
Kwong, Man Kam
1982.
Oscillation of second-order hyperbolic equations with non-integrable coefficients.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 91,
Issue. 3-4,
p.
305.
Travis, C.C.
and
Yoshida, Norio
1982.
Oscillation criteria for nonlinear Bianchi equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 6,
Issue. 6,
p.
625.

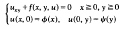
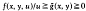 for some function
for some function 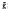 ψ′(
ψ′(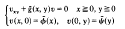
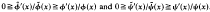 .Some results of Pagan are improved using this approach and a problem posed by him is also studied.
.Some results of Pagan are improved using this approach and a problem posed by him is also studied.